2020-2021学年七年级数学人教版下册教学 6.1 平方根课件(共22张)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册教学 6.1 平方根课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 14:07:39 | ||
图片预览







文档简介
6.1 平方根
第六章 实 数
第1课时 算术平方根
了解算术平方根的概念,会用根号表示一个正数的算术平方根,并了解算术平方根的非负性.
了解开方与乘方互为逆运算,会用平方运算求某些非负数的算术平方根.
学习目标
1
2
我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。
在这五种运算中:
★加法与减法互为逆运算;
★乘法与除法互为逆运算;
★那么乘方与谁互为逆运算呢?
回忆与思考:
继续努力
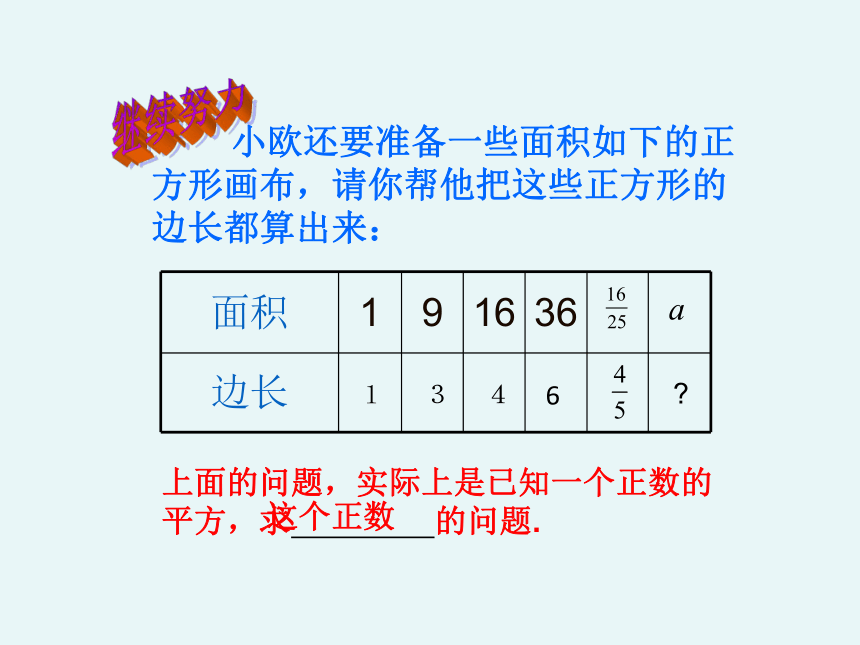
小欧还要准备一些面积如下的正方形画布,请你帮他把这些正方形的边长都算出来:
面积
1
9
16
36
边长
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求 的问题.
?
这个正数
定
义
如果一个正数x的平方等于a,即 x 2 =a ,那么这个
正数x就叫做a的算术平方根,记为“ ”,读作
“ 根号 a ”. a叫做被开方数.
规定:0的算术平方根是0,即
(a≥0)
≥0
非负数
算术平方根具有双重非负性
练一练
1.因为22=4 ,所以4的算术平方根是__;
2.下列说法正确的是 .
①5是25的算术平方根.
② 0.01是0.1的算术平方根.
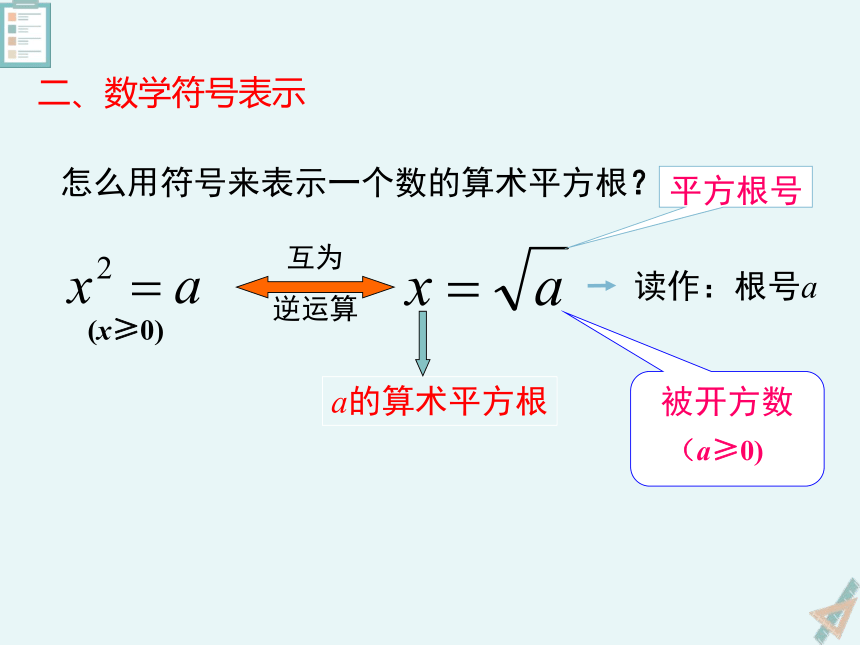
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
二、数学符号表示
表示的意义是什么?它的值是多少?用等式怎样表示?
表示49的算术平方根,它的值是7,用等式表示为 =7
问题解决
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有1个
合作与交流:
三、算术平方根的性质
抢答
361
∵12= 1 ∴ =1 ∵22= ∴ =2
∵32= ∴ =3 ∵42= ∴ =4
∵52= ∴ =5 ∵62= ∴ =6
∵72= ∴ =7 ∵82= ∴ =8
∵92= ∴ =9 ∵102= ∴ =10
∵112= ∴ =11 ∵122= ∴ =12
∵132= ∴ =13 ∵142= ∴ =14
∵152= ∴ =15 ∵162= ∴ =16
∵172= ∴ =17 ∵182= ∴ =18
∵192= ∴ =19 ∵202= 400 ∴ =20
4
9
16
25
81
121
225
49
64
100
144
36
196
169
256
324
289
判断题:下列各式是否有意义?为什么?
有
有
有
无
练一练
例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001
(4) (5)3
学以致用
(1)因为 =100,
所以100的算术平方根为10,
即 =10.
解:
例2 计算:
(1) ; (2) .
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
你会上当吗?
的算术平方根是 .
2
?
3
方法小结:
应该先把这个数算出来
注意文字或算术的表述,读清题意,再进行计算,以防误解.
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
算术平方根的双重非负性
二
例3:自由下落物体下落的距离h(米)与下落时间t(秒)的关系为 .有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将h=19.6代入公式
,
得 ,
所以正数 (秒).
即铁球到达地面需要2秒.
⑴100 ⑵ ⑶0.0001 ⑷81 ⑸32 ⑹
1.求下列各数的算术平方根:
练一练
2.下列式子表示什么意义?你能求出它们的值吗?
解:设每块地板砖的边长为x m.由题意得
故每块地板砖的边长是0.5 m.
3.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
小明想用一块面积为16cm2的正方形纸片,沿边的方向裁出一块面积为12cm2的长方形纸片,使它的长宽之比为3:2,他能裁出吗?
4.解答下列问题:
已知:|x+2y|+
求x-3y+4z的值.
解:由题意得:
解得
拓展提升
同学们,说说这节课的收获吧!
第六章 实 数
第1课时 算术平方根
了解算术平方根的概念,会用根号表示一个正数的算术平方根,并了解算术平方根的非负性.
了解开方与乘方互为逆运算,会用平方运算求某些非负数的算术平方根.
学习目标
1
2
我们已学过了有理数的加法、减法、乘法、除法、乘方这五种运算。
在这五种运算中:
★加法与减法互为逆运算;
★乘法与除法互为逆运算;
★那么乘方与谁互为逆运算呢?
回忆与思考:
继续努力
小欧还要准备一些面积如下的正方形画布,请你帮他把这些正方形的边长都算出来:
面积
1
9
16
36
边长
1
3
4
6
上面的问题,实际上是已知一个正数的平方,求 的问题.
?
这个正数
定
义
如果一个正数x的平方等于a,即 x 2 =a ,那么这个
正数x就叫做a的算术平方根,记为“ ”,读作
“ 根号 a ”. a叫做被开方数.
规定:0的算术平方根是0,即
(a≥0)
≥0
非负数
算术平方根具有双重非负性
练一练
1.因为22=4 ,所以4的算术平方根是__;
2.下列说法正确的是 .
①5是25的算术平方根.
② 0.01是0.1的算术平方根.
a的算术平方根
互为
逆运算
平方根号
被开方数
读作:根号a
(a≥0)
怎么用符号来表示一个数的算术平方根?
(x≥0)
二、数学符号表示
表示的意义是什么?它的值是多少?用等式怎样表示?
表示49的算术平方根,它的值是7,用等式表示为 =7
问题解决
1.一个正数的算术平方根有几个?
0的算术平方根有一个,是0.
2.0的算术平方有几个?
负数没有算术平方根.
3.-1有算术平方根吗?负数有算术平方根?
一个正数的算术平方根有1个
合作与交流:
三、算术平方根的性质
抢答
361
∵12= 1 ∴ =1 ∵22= ∴ =2
∵32= ∴ =3 ∵42= ∴ =4
∵52= ∴ =5 ∵62= ∴ =6
∵72= ∴ =7 ∵82= ∴ =8
∵92= ∴ =9 ∵102= ∴ =10
∵112= ∴ =11 ∵122= ∴ =12
∵132= ∴ =13 ∵142= ∴ =14
∵152= ∴ =15 ∵162= ∴ =16
∵172= ∴ =17 ∵182= ∴ =18
∵192= ∴ =19 ∵202= 400 ∴ =20
4
9
16
25
81
121
225
49
64
100
144
36
196
169
256
324
289
判断题:下列各式是否有意义?为什么?
有
有
有
无
练一练
例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001
(4) (5)3
学以致用
(1)因为 =100,
所以100的算术平方根为10,
即 =10.
解:
例2 计算:
(1) ; (2) .
解:(1)原式=7+3-1=9;
(2)原式=2+3-4=1.
你会上当吗?
的算术平方根是 .
2
?
3
方法小结:
应该先把这个数算出来
注意文字或算术的表述,读清题意,再进行计算,以防误解.
算术平方根具有双重非负性
a的算术平方根
非负数
非负数
算术平方根的双重非负性
二
例3:自由下落物体下落的距离h(米)与下落时间t(秒)的关系为 .有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将h=19.6代入公式
,
得 ,
所以正数 (秒).
即铁球到达地面需要2秒.
⑴100 ⑵ ⑶0.0001 ⑷81 ⑸32 ⑹
1.求下列各数的算术平方根:
练一练
2.下列式子表示什么意义?你能求出它们的值吗?
解:设每块地板砖的边长为x m.由题意得
故每块地板砖的边长是0.5 m.
3.用大小完全相同的240块正方形地板砖,铺一间面积为60 m2的会议室的地面,每块地板砖的边长是多少?
小明想用一块面积为16cm2的正方形纸片,沿边的方向裁出一块面积为12cm2的长方形纸片,使它的长宽之比为3:2,他能裁出吗?
4.解答下列问题:
已知:|x+2y|+
求x-3y+4z的值.
解:由题意得:
解得
拓展提升
同学们,说说这节课的收获吧!
