6.2 黄金分割 同步训练（含解析）

中小学教育资源及组卷应用平台
初中数学苏科版九年级下册6.2
黄金分割
同步训练
一、单选题（本大题共10题，每题3分，共30分）
1.已知点P是线段AB的黄金分割点，且AP＞PB，则有（??
）
A.?AB2=AP?PB??????????????????B.?AP2=BP?AB??????????????????C.?BP2=AP?AB??????????????????D.?AP?AB=PB?AP
2.已知如图，点
是线段
的黄金分割点（
），则下列结论中正确的是（??
）
A.?????????????????B.?????????????????C.?????????????????D.?
3.已知点C是线段AB的黄金分割点，且AC＞BC，如果AB长为20，则AC为（???
）
A.?10
﹣10??????????????????????B.?10﹣10
??????????????????????C.?30﹣10
??????????????????????D.?20﹣10
4.生活中到处可见黄金分割的美．如图，点C将线段AB分成AC、CB两部分，且AC＞BC，如果
，那么称点C为线段AB的黄金分割点．若C是线段AB的黄金分割点，AB＝2，则分割后较短线段长为（??
）
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
5.如图，
是线段
的黄金分割点，且
，若
表示以
为一边的正方形的面积，
表示长为
，宽为
的矩形的面积，则
与
的大小关系是（??
）
?
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?无法确定
6.如图，已知点
是正方形
的边
边上的黄金分割点，且
若
表示
为边长的正方形面积，
表示以
为长，
为宽的矩形面积，
表示正方形
除去
和
剩余的面积，则
的值为（??
）
A.???????????????????????????????B.???????????????????????????????C.???????????????????????????????D.?
7.有以下命题：
①如果线段
是线段
，
，
的第四比例项，则有
；②如果点
是线段
的中点，那么
是
、
的比例中项；③如果点
是线段
的黄金分割点，且
，那么
是
与
的比例中项；④如果点
是线段
的黄金分割点，
，且
，则
．
其中正确的判断有（?
?）
A.?②④????????????????????????????????B.?①②③④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
8.生活中到处可见黄金分割的美，如图，在设计人体雕像时，使雕像的腰部以下a与全身
的高度比值接近0.618，可以增加视觉美感，若图中
为2米，则a约为（??
）
A.?1.24米????????????????????????????????B.?1.38米????????????????????????????????C.?1.42米????????????????????????????????D.?1.62米
9.宽与长的比是
（约0.618）的矩形叫做黄金矩形，黄金矩形蕴藏着丰富的美学价值，给我们以协调和匀称美感.我们可以用这样的方法画出黄金矩形：作正方形
，分别取
的中点
，连接
，以点F为圆心，以
为半径画弧，交
的延长线于点G；作
，交
的延长线于点H，则图中下列矩形是黄金矩形的是（??
）
A.?矩形ABEF?????????????????????????B.?矩形EFCD?????????????????????????C.?矩形EFGH?????????????????????????D.?矩形ABGH
10.古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：点G将一线段
分为两线段
，
，使得其中较长的一段
是全长
与较短的段
的比例中项，即满足
，后人把
这个数称为“黄金分割”数，把点G称为线段
的“黄金分割”点．如图，在
中，已知
，
，若D
，
E是边
的两个“黄金分割”点，则
的面积为（???
）
A.?????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
二、填空题（本大题共8题，每题2分，共16分）
11.已知线段AB=6cm，点C为AB的黄金分割点，且AC＞BC，则AC=________.
12.已知点D是线段AB的黄金分割点，且线段AD的长为2厘米，则最短线段BD的长是________厘米.
13.如图，已知点C、D是线段AB的两个黄金分割点，若线段AB的长10厘米，则线段CD长________厘米．
14.如图，若
是已知线段，经过点
作
，使
；连接
，在
上截取
；在
上截取
，则
________.
15.大自然是美的设计师，即使是一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么AP的长度为________cm．
16.古希腊时期，人们认为最美人体的肚脐至脚底的长度与身高长度之比是
（
0.618，称之为黄金分割比例），著名的“断臂维纳斯”便是如此，若某位女性身高为165cm
，
肚脐到头顶高度为65cm
，
则其应穿鞋跟为________cm的高跟鞋才能使人体近似满足黄金分割比例．（精确到1cm）
17.电视节目主持人在主持节目时，站在舞台的黄金分割点处最自然得体．如图：若舞台AB长为20m，试计算主持人应走到离A点至少________m处．（结果精确到0.1m）
18.如图，在矩形
中，
，
，
是
的黄金分割点（
），
是
上一点，将
沿直线
折叠，点
落在
边上的点
处，再将
沿直线
折叠，点
落在
上的点
处，则
的长为________．
三、解答题（本大题共9题，共84分）
19.已知线段AB=a，用直尺和圆规求作这条线段的黄金分割点C．
?
20.如图，已知线段AB，P1是AB的黄金分割点（AP1＞BP1），点O是AB的中点，P2是P1关于点O的对称点．求证：P1B是P2B和P1P2的比例中项．
21.如图，乐器上的一根弦AB=80cm，两个端点A、B固定在乐器板面上，支撑点C是靠近点B的黄金分割点，支撑点D是靠近点A的黄金分割点，求C、D之间的距离．
?
22.人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段．一个身高1.70m的人，他的肚脐到脚底的长度为多少时才是黄金身段（保留两位小数）？
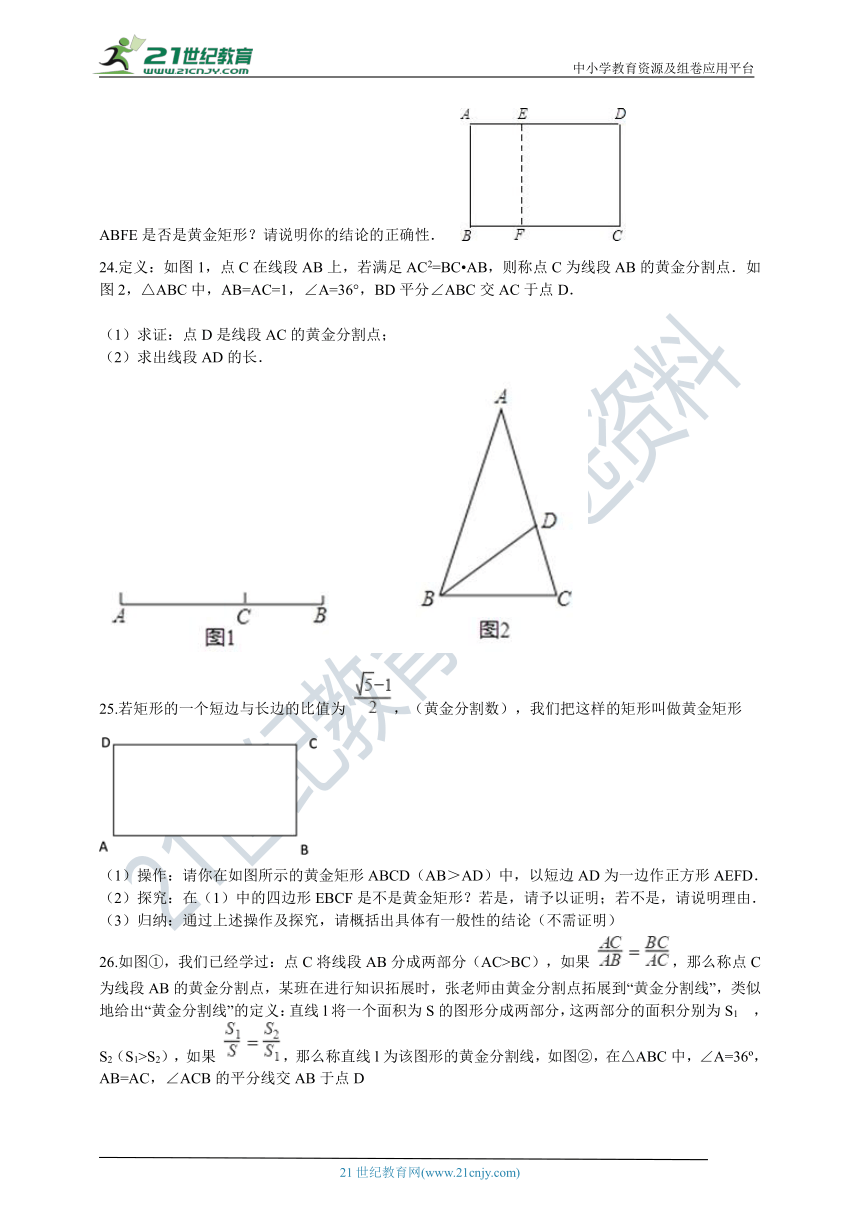
23.如果一个矩形ABCD（AB＜BC）中，
≈0.618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE（如图），请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性．
24.定义：如图1，点C在线段AB上，若满足AC2=BC?AB，则称点C为线段AB的黄金分割点．如图2，△ABC中，AB=AC=1，∠A=36°，BD平分∠ABC交AC于点D．
（1）求证：点D是线段AC的黄金分割点；
（2）求出线段AD的长．
?
25.若矩形的一个短边与长边的比值为
，（黄金分割数），我们把这样的矩形叫做黄金矩形
（1）操作：请你在如图所示的黄金矩形ABCD（AB＞AD）中，以短边AD为一边作正方形AEFD．
（2）探究：在（1）中的四边形EBCF是不是黄金矩形？若是，请予以证明；若不是，请说明理由．
（3）归纳：通过上述操作及探究，请概括出具体有一般性的结论（不需证明）
26.如图①，我们已经学过：点C将线段AB分成两部分（AC>BC），如果
，那么称点C为线段AB的黄金分割点，某班在进行知识拓展时，张老师由黄金分割点拓展到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1
，
S2（S1>S2），如果
，那么称直线l为该图形的黄金分割线，如图②，在△ABC中，∠A=36?，AB=AC，∠ACB的平分线交AB于点D
（1）求证：点D是AB边上的黄金分割点；
（2）求证：直线CD是△ABC的黄金分割点
27.定义：如图1，点P为线段AB上一点，如果
=k，那么我们称点P是线段AB的黄金分割点，
叫做黄金分割数.
?
（1）理解：利用图1，运用一元二次方程的知识，求证：黄金分割数
；
（2）应用：如图2，抛物线y＝x2+nx＋2n（n<0）的图象与x轴交于A、B两点（OA答案解析部分
一、单选题
1.【答案】
B
【考点】黄金分割
解：∵P为线段AB的黄金分割点，且AP＞BP，
∴AP2=BP?AB.
故答案为：B.
分析：黄金分割是指把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。其比值是（√5-1）：2，取其小数点后三位的近似值是0.618；根据黄金分割的意义可求解.
2.【答案】
C
【考点】黄金分割
解：∵点
是线段
的黄金分割点（
），
∴
，
∴选项C是正确的.
故答案为：C.
分析：根据黄金分割点的定义：一个线段分为两部分，较长部分与整体的比和较短线段与较长线段的比都为1:0.618即可得出答案.
3.【答案】
A
【考点】黄金分割
解：∵C是线段AB的黄金分割点，且AC＞BC，
∴AC＝
，
∵AB＝20，
∴AC＝
×20＝10
﹣10．
故答案为：A．
分析：根据黄金分割的定义，知AC为较长线段，则AC＝
，代入数据即可得出AC的值．
4.【答案】
B
【考点】黄金分割
解：根据黄金分割点的概念得：AC=
∴BC=AB-AC=?
；
故答案为：B．
分析：根据黄金分割点的概念进行计算，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值?叫做黄金比．
5.【答案】
B
【考点】黄金分割
解：∵P是线段AB的黄金分割点，且PA＞PB，
∴PA2=PB?AB，
又∵S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，
∴S1=PA2
，
S2=PB?AB，
又∵PA2=PB?AB，
∴S2=
PA2
．
∴S1=S2
．
故答案为：B．
分析：根据黄金分割的定义得出PA2=PB?AB，根据题意得出S1=PA2
，
S2=PB?AB，即可得出S1=S2
．
6.【答案】
A
【考点】黄金分割
解：设正方形ABCD的边长为a
，
∵点E是AB上的黄金分割点，
∴
，则
，
∴
，则
，
∵
，
，
∴
，
∴
．
故答案为：A．
分析：根据黄金分割的定义作答即可。
7.【答案】
C
【考点】比例的性质，黄金分割，相似三角形的判定与性质
解：①如果线段
是线段
，
，
的第四比例项，则有
，符合题意②如果点
是线段
的中点，则
，
所以
，
所以
不是
、
的比例中项，不符合题意；③如果点
是线段
的黄金分割点，且
，
则
，
所以
，即
，
所以
是
与
的比例中项，符合题意；④如果点
是线段
的黄金分割点，
，且
，
则
，即
，
所以
，符合题意；
综上，正确的判断有①③④，
故答案为：C．
分析：根据比例线段、黄金分割的定义逐项判定即可。
8.【答案】
A
【考点】黄金分割
解：由题意可知，a:b≈0.618，代入b=2，
∴a≈2×0.618=1.236≈1.24.
故答案为：A
分析：根据a:b≈0.618，且b=2即可求解.
9.【答案】
D
【考点】勾股定理，正方形的性质，黄金分割
解：设正方形的边长为2，则CD＝2，CF＝1
在直角三角形DCF中，DF＝
∴FG＝
∴CG＝
?1
∴
∴矩形DCGH为黄金矩形
故答案为：D.
分析：先根据正方形的性质以及勾股定理，求得DF的长，再根据DF＝GF求得CG的长，最后根据CG与CD的比值为黄金比，判断矩形DCGH为黄金矩形.
10.【答案】
A
【考点】三角形的面积，等腰三角形的性质，黄金分割
解：过点A作AF⊥BC，
∵AB=AC，
∴BF=
BC=2，
在Rt
,AF=
，
∵D是边
的两个“黄金分割”点，
∴
即
，
解得CD=
，
同理BE=
，
∵CE=BC-BE=4-(
-2)=6-
，
∴DE=CD-CE=4
-8，
∴S△ABC=
=
=
，
故答案为：A.
分析：作AF⊥BC，根据等腰三角形ABC的性质求出AF的长，再根据黄金分割点的定义求出BE、CD的长度，得到
中DE的长，利用三角形面积公式即可解题.
二、填空题
11.【答案】
【考点】黄金分割
解：已知AC＞BC且AB=6cm，根据黄金分割点的概念可得AC=
=
cm.
分析：由黄金分割点，可得AC=
，据此计算即可.
12.【答案】
【考点】黄金分割
解：因为点D是线段AB的黄金分割点，且BD＜AD
所以
因为AD的长为2厘米
所以代入解得
故答案为：.
分析：根据黄金分割定义，将一条线段分割成长短两条线段，其中较长线段与整条线段的比=较短线段与较长线段的比=
，
即可建立方程，求解即可.
13.【答案】
10
-20
【考点】黄金分割
解：∵C、D为线段AB的黄金分割点，AB=10，
∴AC=
AB=5
-5，BD=
AB=5
-5，
所以CD=2（5
-5）-10=10
-20.
分析：根据黄金比值是，
进行计算即可
14.【答案】
【考点】黄金分割
解：设
，则
，
在
中，
，
，
，
，
，
，
故答案为：
.
分析：由已知条件BD=AB可设BD=a，AB=2a，在直角三角形ABD中，用勾股定理可将AD用含a的代数式表示，则AE=AD-DE也可用含a的代数式表示，由作图可知AE=AC，则可求解.
15.【答案】
5
-5
【考点】黄金分割
解：∵P为AB的黄金分割点（AP＞PB），
∴AP＝
?AB＝
×10＝5
﹣5（cm），
故答案为：5
﹣5
分析：根据黄金分割的定义，PA就是AB与PB的比例中项，从而列出方程，进而得出AP＝
?AB，将AB的长度代入即可算出答案。
16.【答案】
5
【考点】黄金分割
解：设
她应选择高跟鞋的高度是
cm，
则
≈0.618，
解得：x≈5，且正确．
故答案为：5．
分析：根据黄金分割的概念，列出方程直接求解即可．
17.【答案】
7.6
【考点】黄金分割
解：根据黄金比得：20×（1-0.618）≈7.6米或20×
≈12.4米（舍去），
则主持人应走到离A点至少7.6米处．
故答案为：7.6
分析：把一条线段分割为两部分，使较大部分与全长的比值等于较小部分与较大的比值，这个比值即为黄金分割，这个点为黄金分割点.其比值是≈0.618.此题要求主持人至少走离A点多少米，根据黄金比，只需要走到AB的1-0.618倍处即得.
18.【答案】
【考点】翻折变换（折叠问题），黄金分割
解：∵
，
是
的黄金分割点（
），
∴
∴
由折叠的性质可得：四边形ABFE和四边形EHGD是正方形，
∴
，
∴
；
故答案为：
分析：先根据黄金分割得出AE和DE的长，再根据折叠的性质得出正方形ABFE和正方形EHGD，从而得出EF=AE，EH=DE即可得出结论
三、解答题
19.【答案】
解：作法：
（1）延长线段AB至F，使AB=BF，分别以A、F为圆心，以大于等于线段AB的长为半径作弧，两弧相交于点G，连接BG，则BG⊥AB，在BG上取点D，使BD=；
（2）连接AD，在AD上截取DE=DB．
（3）在AB上截取AC=AE．
如图，点C就是线段a的黄金分割点．
【考点】黄金分割
分析：把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值（
）叫做黄金比．
20.【答案】证明：设AB=2，
∵P1是AB的黄金分割点（AP1＞BP1），
∴AP1=
×2=
﹣1，
∴P1B=2﹣（
﹣1）=3﹣
，
∵点O是AB的中点，
∴OB=1，
∴OP1=1﹣（3﹣
）=
﹣2，
∵P2是P1关于点O的对称点，
∴P1P2=2（
﹣2）=2
﹣4，
∴P2B=2
﹣4+3﹣
=
﹣1，
∵P1B2=（3﹣
）2=14﹣6
，P2B?P1P2=（
﹣1）（2
﹣4）=14﹣6
，
∴P1B2=P2B?P1P2
，
∴P1B是P2B和P1P2的比例中项
【考点】黄金分割
分析：设AB=2，根据黄金分割的定义得AP1=
AB=
﹣1，则P1B=3﹣
，由点O是AB的中点得OB=1，所以OP1=
﹣2，由于P2是P1关于点O的对称点，则P1P2=2
﹣4，可计算出P2B=
﹣1，然后同过计算得到P1B2=14﹣6
，P2B?P1P2=14﹣6
，即P1B2=P2B?P1P2
，
所以P1B是P2B和P1P2的比例中项．
21.【答案】
解：∵点C是靠近点B的黄金分割点，点D是靠近点A的黄金分割点，
∴AC=BD=80×
=40﹣40，
∴CD=BD﹣（AB﹣BD）=2BD﹣AB=80﹣160．
【考点】黄金分割
分析：根据黄金分割的概念和黄金比值计算即可．
22.【答案】解：设他的肚脐到脚底的长度为xm时才是黄金身段，
根据题意得x：1.70=0.618，
即x=1.70×0.618≈1.1（m）．
答：他的肚脐到脚底的长度为1.1m时才是黄金身段
【考点】黄金分割
分析：他的肚脐到脚底的长度为xm时才是黄金身段，根据肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段，则x：1.70=0.618，然后解方程即可．
23.【答案】解：矩形ABFE是黄金矩形．
∵AD=BC，DE=AB，
∴
=
=
﹣1=
=
．
∴矩形ABFE是黄金矩形
【考点】正方形的性质，黄金分割
分析：只需求得其宽与长的比是否符合黄金比即可．
24.【答案】
（1）证明：∵AB=AC=1，
∴∠ABC=∠C=（180°﹣∠A）=（180°﹣36°）=72°，
∵BD平分∠ABC交AC于点D，
∴∠ABD=∠CBD=∠ABC=36°，
∴∠BDC=180°﹣36°﹣72°=72°，
∴DA=DB，BD=BC，
∴AD=BD=BC，
易得△BDC∽△ABC，
∴BC：AC=CD：BC，即BC2=CD?AC，
∴AD2=CD?AC，
∴点D是线段AC的黄金分割点；
（2）设AD=x，则CD=AC﹣AD=1﹣x，
∵AD2=CD?AC，
∴x2=1﹣x，解得x1=，
x2=，
即AD的长为．
【考点】黄金分割
分析：（1）利用等腰三角形的性质和三角形内角和定理可计算出∠ABC=∠C=72°，∠ABD=∠CBD=36°，∠BDC=72°，则可得
到AD=BD=BC，然后根据相似三角形的判定方法易得△BDC∽△ABC，利用相似比得到BC2=CD?AC，于是有AD2=CD?AC，则可根据线段黄金分割点的定义得到结论；
（2）设AD=x，则CD=AC﹣AD=1﹣x，由（1）的结论得到x2=1﹣x，然后解方程即可得到AD的长．
25.【答案】
（1）解：以AD为边可作出两个正方形AEFD与AE′F′D′（AB＞AD），如图所示
（2）解：矩形EBCF不是黄金矩形，理由如下：
设AB=a，AD=b（a＞b），则BE=BA+AE=a+b，BE′=BA-E′A=a-b，
由ABCD为黄金矩形，得
=
∴
=
=
÷（1+
）=
÷（1+
）=
≠
∴矩形EBCF不是黄金矩形;
矩形E′BCF′是黄金矩形.
证明：如图，∵
=
=（1-
）÷
=（1-
）÷
=
∴E′BCF′是黄金矩形
（3）解：由（1）、（2）可发现结论：若以黄金矩形的短边为边在矩形内作（截割）正方形，则剩余矩形必为黄金矩形.
【考点】黄金分割，相似多边形的性质
分析：（1）如图，分两种情况：正方形中，AD的对边在矩形的内部或外部；
（2）矩形EBCF不是黄金矩形，
设AB=a，AD=b（a＞b），则BE=BA+AE=a+b，BE′=BA-E′A=a-b，由已知得
=
，所以
=
=
÷（1+
）=
÷（1+
）=
≠
，对应边不成比例，故矩形EBCF不是黄金矩形；矩形E′BCF′是黄金矩形，
理由：
=
=（1-
）÷
=（1-
）÷
=
，即对应边成比例，故两个矩形相似.（3）由（1）、（2）可发现结论：若以黄金矩形的短边为边在矩形内作（截割）正方形，则剩余矩形必为黄金矩形.
26.【答案】
（1）证明：解:（1）点D是边AB上的黄金分割点，理由如下:
∵∠A=36°，AB=AC，∴∠B=∠ACB=72°.
∵CD平分∠ACB，∴∠ACD=∠DCB=36°，
∴∠BDC=∠B=72°，∠ACD=∠A=36°，
∴BC=DC=AD.
∵∠A=∠BCD，∠B=∠B，
∴
，
∴
∴
∵.D是AB边上的黄金分割点，
（2）证明：直线CD是△ABC的黄金分割线，理由如下:
设△ABC的边AB上的高为h，则
∵D是AB的黄金分割点，
∴
∴
∴CD是△ABC的黄金分割线.
【考点】三角形的面积，等腰三角形的判定与性质，黄金分割，相似三角形的判定与性质
分析：（1）根据等腰三角形的性质及角平分线的定义得出BC=DC=AD，证出?BCD∽?BAC，得出，
从而得出，
即可得出
D是AB边上的黄金分割点；
（2）利用三角形的面积公式得出，
，
由，
得出，
即可得出直线CD是△ABC的黄金分割点.
?
27.【答案】
（1）证明：设
，
，则
，
由
得：
，
即
，
解得
，
∵
，
∴
，
；
（2）解：①设
，
，则
，
，
，
由二次函数与一元二次方程的联系得：
，
是方程
的两根，
∴
，
，
∵原点
是线段
的黄金分割点，且
，
∴
，即
，
∴
，
整理得：
，
∴
，
∴
，
即
；②
，
.
?
【考点】公式法解一元二次方程，一元二次方程的根与系数的关系，黄金分割
解：（2）②由（2）①得：
，
由黄金分割点的定义得：
，
解得
，
则
，
故
，
.
分析：（1）设
，
，从而可得
，再根据黄金分割点的定义建立方程，然后利用公式法解一元二次方程即可得；
（2）①设
，
，从而可得
，
，
，再根据一元二次方程根与系数的关系可得
，
，然后根据黄金分割点的定义可得
，从而可得
，由此化简即可得；②根据①的结论，利用黄金分割点的定义分别求出OA、OB的长，由此即可得.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
（共
2
页）
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)