高中物理必修Ⅰ人教版3.2 弹力同步课件(48张ppt)
文档属性
| 名称 | 高中物理必修Ⅰ人教版3.2 弹力同步课件(48张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-08 15:17:27 | ||
图片预览










文档简介
(共48张PPT)
第三节
弹力
弹力、摩擦力都属于—接触力
接触力:物体与物体直接接触才发生的力。
1、通常所说的拉力、支持力、阻力等都是接触力。
2、接触力按性质可归纳为:
弹力和摩擦力
(它们在本质上都是由电磁相互作用引起的)
一、形变
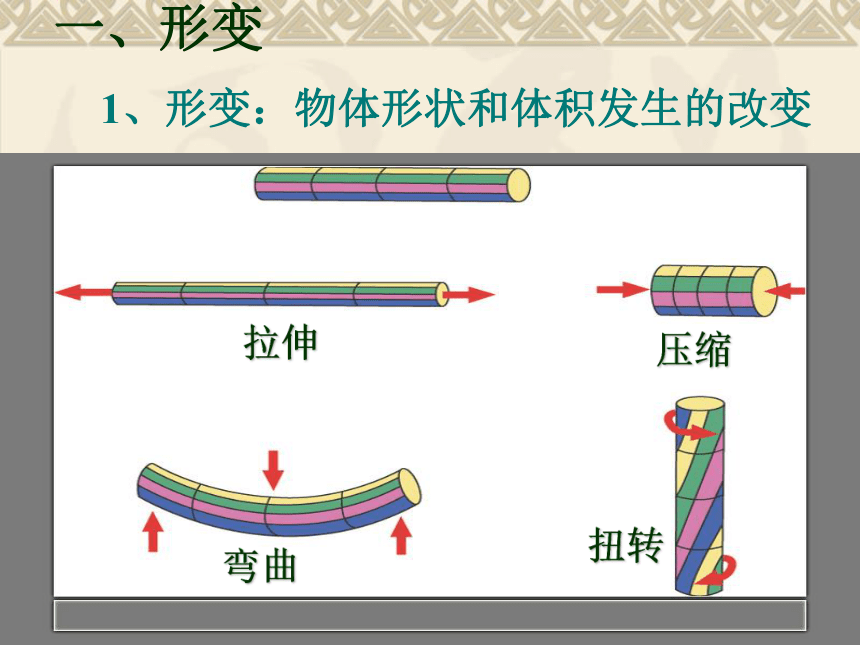
1、形变:物体形状和体积发生的改变
拉伸
压缩
弯曲
扭转
一、形变
(拉伸、压缩、弯曲、扭转等等)
桌上子放着本书,书和桌面有没有发生形变呢?
问题
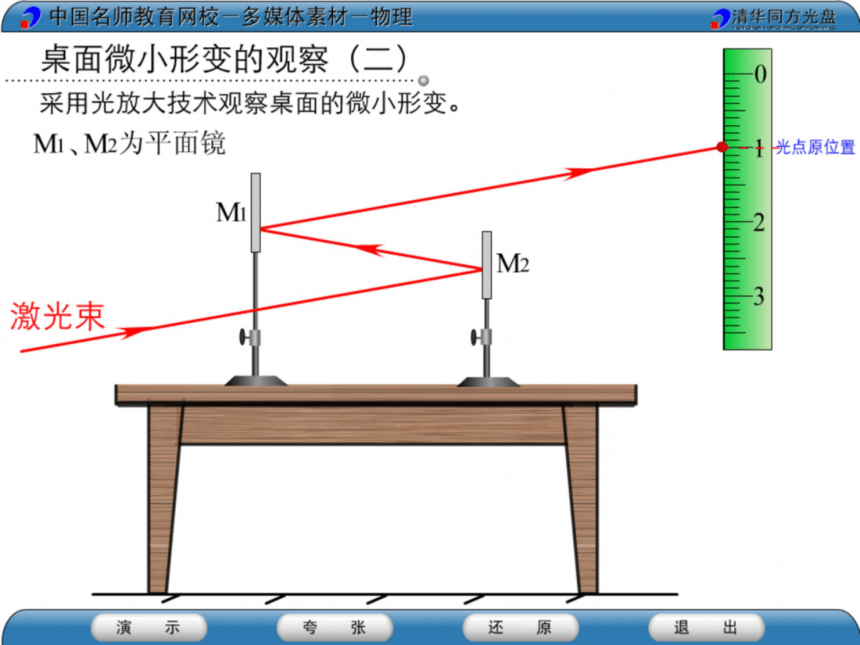
有一些物体眼睛根本观察不到它的形变,
比如一些比较坚硬的物体,但是这些物体
都有形变,只不过形变很微小。
一切物体都在力的作用下都会发生形变。
由于书压桌面,所以桌面产生向下的形变——桌面恢复性变对书产生支持力
由于桌子支持书,所以书本产生向上的形变——书恢复性变对桌子产生压力
手挤压玻璃瓶,观察水柱的变化。
(微小形变的演示)
2、形变的分类
1)按形变程度分
2)按可否恢复分
明显形变
微小形变
非弹性形变
(也叫范性形变)
弹性形变
发生形变的物体在停止受力后,能恢复原状的形变称为弹性形变
弹性限度
如果形变过大,超过一定限度,即使撤去作用力,物体也不能完全恢复原来的形状,这个限度叫弹性限度
范 性 形 变
二、弹力:
指发生弹性形变的物体由于要恢复原样,对与它接触的物体产生力的作用
作用过程
二、弹力:
施力物体:
发生形变的物体
受力物体:
与施力物体接触,使它发生形变,并阻碍其恢复原状的物体
产生的条件(原因)
1、物体间相互接触
2、物体发生弹性形变
接触力
例1
关于弹力的产生下列说法(
)
A、只要两物体接触就一定产生弹力
B、只要两物体相互吸引就一定产生弹力
C、只要两物体发生形变就一定产生弹力
D、只有发生弹性形变的物体才会对与它接触的物体产生弹力作用
A
B
C
例2、分析A对C有无弹力作用
D
二、弹力的方向:
从施力物体指向受力物体,与施力物体形变方向相反(施力物体恢复形变的方向)。
受力分析
只分析物体所受的力
静止在地面上的篮球
G
N
例
题
分析书放在桌面或倾斜木板上时,
书和木板所受的弹力
书
木板
书
板
N1
N1
N2
N2
例1:放在水平桌面上的书
书由于重力的作用而压迫桌面,使书和桌面同时发生微小形变,要恢复原状,对桌面产生垂直于桌面向下的弹力F1,这就是书对桌面的压力;桌面由于发生微小的形变,对书产生垂直于书面向上的弹力F2,这就是桌面对书的支持力。
各种接触面间的弹力方向判断:''垂直于接触面'
曲面与平面接触
N
N
N`
曲面与平面间弹力方向:
过接触点垂直平面指向受力物体
各种接触面间的弹力方向判断
点与平面接触
N
N`
点与平面间弹力方向:
过接触点垂直平面指向受力物体
光滑斜面
A
B
NA
NB
各种接触面间的弹力方向判断
点与曲面接触
点与曲面间弹力方向:
与过接触点的切面垂直并指向受力物体
N1
N2
半球形的碗
A
B
NA
NB
各种接触面间的弹力方向判断
曲面与曲面接触
曲面与曲面间弹力方向:
与过接触点的公切面垂直并指向受力物体
半球形的碗
N
A
B
N
NB对A
判断下列支持面对物体弹力的方向
平面与平面接触,弹力垂直平面。
点与平面接触,弹力通过接触点而垂直平面。
曲面和曲面接触,弹力通过接触点垂直于公切面。(相当于点与点)
判断下列支持面对物体弹力的方向
点和曲面接触,弹力通过接触点垂直于切面
点和线接触,弹力通过接触点垂直于线
总结:绳上弹力方向
总是沿着绳而指向绳子收缩的方向
绳子的拉力也是弹力,那么绳子的拉力的方向如何呢?
轻绳的受力特点:
1、只能拉不能压;
2、轻绳的拉力一定沿绳方向;
3、同一根绳子张力处处相等。
轻绳受力特点
G
Ta
Tb
a
b
例如
A
A
分析下列物体所受的力
A
B
B
G
T
A
G`
T2
T1
1
2
例:画出下列物体所受到的所有弹力。
轻杆受力特点
轻杆的含义:
不计质量不发生形变的杆
轻杆受力特点:
1、可拉可压;
2、杆所受的力不一定沿杆的方向;可能沿任意方向
轻杆分析受力主要是依据平衡特点
我们对弹力方向做一个总结
1、弹簧两端的弹力方向,与弹簧中心轴线重合,指向弹簧恢复原状方向
2、轻绳(或橡皮条)对物体的弹力方向,沿绳指向绳收缩的方向
3、点与面接触时的弹力方向,过接触点垂直于接触面(或接触面切线方向)而指向受力物体。
4、平面与平面接触时弹力的方向,垂直于接触面而指向受力物体
5、曲面与平面接触时弹力的方向,在接触点与球心的连线上而指向受力物体
6、曲面与曲面相接触时弹力的方向,垂直过接触点的分切面,通过两球球心而指向受力物体
弹力有无的判断
对于微小形变,用假设推理法:假设有弹力看是否能保持现在的状态!
A
B
光滑水平面并排放着静止的木块A、B
假设A、B间有弹力
以B为研究对象,B受力:
G
N地
NA→B
B不可能静止,所以A、B间没有弹力
弹力有无的判断
判断球与斜面间有无弹力。已知绳子竖直状态
假设球与斜面间有弹力
以球为研究对象,球受力:
G
T
N斜面→球
球不可能静止,同时绳子不可能竖直。所以球与斜面间没有弹力
弹力有无的判断
光滑球静止在水平地面
假设球与木块间有弹力
以球为研究对象,球受力:
G
N
N木块→球
球不可能静止,所以球与斜面间没有弹力
例:画出下列物体所受到的所有弹力。
水平面上的球
弹力的作用点和大小
1、弹力的作用点:两物体接触处,在受力物体上。
2、对于同一物体,弹力大小同形变大小有关。
利用力的平衡来计算
利用牛顿第二定律
弹簧弹力大小计算——
胡克定律
两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连,A静止于水平地面上,如图3-2-8所示.不计摩擦,A对绳的作用力的大小与地面对A的作用力的大小分别为多少?
弹簧弹力方向又什么样的呢?
弹簧两端的弹力方向,与弹簧中心轴线重合,指向弹簧恢复原状方向.
实验目的
1、探究弹力与
的定量关系。
2、学会利用图象研究两个物理量之间的关系的方法。
实验原理
1、如图所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧产生的弹力与
大小相等。
2、用刻度尺测出弹簧在不同的钩码拉力下的伸长量x,建立坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描写实验所测得的各组(x,F)对应的点,用
的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系。
弹簧伸长
所挂钩码的重力
平滑
探究弹力与弹簧伸长量的关系
五、胡克定律:
实验器材
轻质弹簧(一根),钩码(一盒),刻度尺,铁架台,重垂线,坐标纸,三角板
实验步骤
1、如图所示,将铁架台放于桌面上(固定好),将弹簧的一端固定于铁架台的横梁上,在挨近弹簧处将刻度尺(最小分度为mm)固定于铁架台上,并用
检查刻度尺是否竖直。
重垂线
2、记下弹簧下端不挂钩码时所对应的刻度L0
3、在弹簧下端挂上一个钩码,待钩码静止后,记下弹簧下端所对应的刻度L1
4、用上面方法,记下弹簧下端挂2个、3个、4个…
…钩码时,弹簧下端所对应的刻度L2、L3、L4
…
…,并将所得数据记录在表格中
5、用xn=Ln-L0计算出弹簧挂1个、2个、3个…
…钩码时弹簧的伸长量,并根据当地重力加速度值g,计算出所挂钩码的总重力,这个总重力就等于
的大小,将所得数据填入表格。
弹簧弹力
6、根据所测数据在坐标纸上描点,最好以弹簧弹力为纵坐标,以弹簧的伸长量为横坐标。
7、按照图中各点的分布与走向,尝试作出一条平滑的曲线(包括直线)。所画的点不一定正好都在这条曲线上,但要注意使曲线两侧的点数大致相同。
8、以弹簧的伸长为自变量,写出曲线所代表的函数,首先尝试一次函数,如果不行,则考虑二次函数。
9、解释函数表达式中常数的物理意义。
实验现象及注意事项
1、随着所挂钩码数量的增多,弹簧会越来越长,实验时,弹簧下端所挂钩码不宜太多,以免超出弹簧的弹性限度。
2、在建立坐标系描点时,我们要探求的是弹簧的伸长量与弹力大小的关系,而不是弹簧的总长度。
3、实验中外力的大小(即钩码的重力)与弹力的大小是相等的。
4、测原长时必须把弹簧竖直挂起来
五、胡克定律:
实验:探究弹力和弹簧伸长的关系
1、内容:
弹簧发生弹性形变时,弹力的大小跟弹簧伸长(或缩短)的长度x成正比。
2、公式:
F
=
k
x
其中:k——弹簧的劲度系数
(与弹簧的丝的粗细、材料、弹簧的直径、绕法和长度等量有关)
单位:牛每米,
符号N/m
x——弹簧伸长(或缩短)的长度
例1、下列关于弹力的说法不正确是?
A、只要两个物体接触就一定能产生弹力
B、两个接触并发生弹性形变的物体一定产生弹力
C、压力、支持力、拉力都是弹力
D、压力、支持力的方向总是垂直于支持面
例2、关于胡克定律F=kx中的x,下列说法正确的是?
A、x是弹簧伸长后或压缩后的长度
B、x是弹簧原来的长度
C、x是弹簧变化(伸长或压缩)的长度
D、x是弹簧原长加后来的长度
A
C
如图3-2-5所示,为一轻质弹簧的长度L和弹力F大小的关系,试由图线确定:
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧长为0.2m时弹力的大小.
(1)10cm
(2)200N/m
(3)20N
GA=100N,GB=40N,弹簧的劲度系数为500N/m,不计绳重和摩擦,求:物体A对支持面的压力和弹簧的伸长量。
小结
一、弹力产生条件:
①
直接接触
②
发生弹性形变
二、弹力方向
1、压力和支持力:
方向都垂直于接触面指向被压或被支持的物体。
2、拉力:
绳的拉力沿着绳指向绳
收缩的方向
三、弹力大小:
1、弹簧弹力:胡克定律F
=
k
x
2、其它弹力:由物体受其它力和运动状态求解
如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置。静止时B对A的弹力为F1,C对B的弹力为F2,则:(
)
A、F1=mg,F2=2mg B、F1>mg,F2=2mg
C、F1<mg,F2=2mg
D、F1>mg,F2>2mg
N
S
N
S
A
B
C
B
两根长均为20cm的弹簧,劲度系数分别为k1=200N/m,k2=100N/m,弹簧k2固定在A上,弹簧k1固定在A、B上,B放在水平地面上,弹簧竖直,如图所示。已知A、B所受的重力都是4N,今在k2的端点P施加一个竖直向上的力,缓慢地向上拉,当P点向上升距离为多少
时,B和地面恰好接触而没有作用力。弹簧自重不计。
如图A、B两物体重力分别是GA=3N、GB=4N,A用悬绳挂在天花板上,B放在水平地面上,A、B间的轻弹簧的弹力F=2N,则绳中张力FT和B对地面的压力FN的可能值分别为
C、1N和6N
D、2N和5N
A、7N和0N
B、5N和2N
(
BC
)
第三节
弹力
弹力、摩擦力都属于—接触力
接触力:物体与物体直接接触才发生的力。
1、通常所说的拉力、支持力、阻力等都是接触力。
2、接触力按性质可归纳为:
弹力和摩擦力
(它们在本质上都是由电磁相互作用引起的)
一、形变
1、形变:物体形状和体积发生的改变
拉伸
压缩
弯曲
扭转
一、形变
(拉伸、压缩、弯曲、扭转等等)
桌上子放着本书,书和桌面有没有发生形变呢?
问题
有一些物体眼睛根本观察不到它的形变,
比如一些比较坚硬的物体,但是这些物体
都有形变,只不过形变很微小。
一切物体都在力的作用下都会发生形变。
由于书压桌面,所以桌面产生向下的形变——桌面恢复性变对书产生支持力
由于桌子支持书,所以书本产生向上的形变——书恢复性变对桌子产生压力
手挤压玻璃瓶,观察水柱的变化。
(微小形变的演示)
2、形变的分类
1)按形变程度分
2)按可否恢复分
明显形变
微小形变
非弹性形变
(也叫范性形变)
弹性形变
发生形变的物体在停止受力后,能恢复原状的形变称为弹性形变
弹性限度
如果形变过大,超过一定限度,即使撤去作用力,物体也不能完全恢复原来的形状,这个限度叫弹性限度
范 性 形 变
二、弹力:
指发生弹性形变的物体由于要恢复原样,对与它接触的物体产生力的作用
作用过程
二、弹力:
施力物体:
发生形变的物体
受力物体:
与施力物体接触,使它发生形变,并阻碍其恢复原状的物体
产生的条件(原因)
1、物体间相互接触
2、物体发生弹性形变
接触力
例1
关于弹力的产生下列说法(
)
A、只要两物体接触就一定产生弹力
B、只要两物体相互吸引就一定产生弹力
C、只要两物体发生形变就一定产生弹力
D、只有发生弹性形变的物体才会对与它接触的物体产生弹力作用
A
B
C
例2、分析A对C有无弹力作用
D
二、弹力的方向:
从施力物体指向受力物体,与施力物体形变方向相反(施力物体恢复形变的方向)。
受力分析
只分析物体所受的力
静止在地面上的篮球
G
N
例
题
分析书放在桌面或倾斜木板上时,
书和木板所受的弹力
书
木板
书
板
N1
N1
N2
N2
例1:放在水平桌面上的书
书由于重力的作用而压迫桌面,使书和桌面同时发生微小形变,要恢复原状,对桌面产生垂直于桌面向下的弹力F1,这就是书对桌面的压力;桌面由于发生微小的形变,对书产生垂直于书面向上的弹力F2,这就是桌面对书的支持力。
各种接触面间的弹力方向判断:''垂直于接触面'
曲面与平面接触
N
N
N`
曲面与平面间弹力方向:
过接触点垂直平面指向受力物体
各种接触面间的弹力方向判断
点与平面接触
N
N`
点与平面间弹力方向:
过接触点垂直平面指向受力物体
光滑斜面
A
B
NA
NB
各种接触面间的弹力方向判断
点与曲面接触
点与曲面间弹力方向:
与过接触点的切面垂直并指向受力物体
N1
N2
半球形的碗
A
B
NA
NB
各种接触面间的弹力方向判断
曲面与曲面接触
曲面与曲面间弹力方向:
与过接触点的公切面垂直并指向受力物体
半球形的碗
N
A
B
N
NB对A
判断下列支持面对物体弹力的方向
平面与平面接触,弹力垂直平面。
点与平面接触,弹力通过接触点而垂直平面。
曲面和曲面接触,弹力通过接触点垂直于公切面。(相当于点与点)
判断下列支持面对物体弹力的方向
点和曲面接触,弹力通过接触点垂直于切面
点和线接触,弹力通过接触点垂直于线
总结:绳上弹力方向
总是沿着绳而指向绳子收缩的方向
绳子的拉力也是弹力,那么绳子的拉力的方向如何呢?
轻绳的受力特点:
1、只能拉不能压;
2、轻绳的拉力一定沿绳方向;
3、同一根绳子张力处处相等。
轻绳受力特点
G
Ta
Tb
a
b
例如
A
A
分析下列物体所受的力
A
B
B
G
T
A
G`
T2
T1
1
2
例:画出下列物体所受到的所有弹力。
轻杆受力特点
轻杆的含义:
不计质量不发生形变的杆
轻杆受力特点:
1、可拉可压;
2、杆所受的力不一定沿杆的方向;可能沿任意方向
轻杆分析受力主要是依据平衡特点
我们对弹力方向做一个总结
1、弹簧两端的弹力方向,与弹簧中心轴线重合,指向弹簧恢复原状方向
2、轻绳(或橡皮条)对物体的弹力方向,沿绳指向绳收缩的方向
3、点与面接触时的弹力方向,过接触点垂直于接触面(或接触面切线方向)而指向受力物体。
4、平面与平面接触时弹力的方向,垂直于接触面而指向受力物体
5、曲面与平面接触时弹力的方向,在接触点与球心的连线上而指向受力物体
6、曲面与曲面相接触时弹力的方向,垂直过接触点的分切面,通过两球球心而指向受力物体
弹力有无的判断
对于微小形变,用假设推理法:假设有弹力看是否能保持现在的状态!
A
B
光滑水平面并排放着静止的木块A、B
假设A、B间有弹力
以B为研究对象,B受力:
G
N地
NA→B
B不可能静止,所以A、B间没有弹力
弹力有无的判断
判断球与斜面间有无弹力。已知绳子竖直状态
假设球与斜面间有弹力
以球为研究对象,球受力:
G
T
N斜面→球
球不可能静止,同时绳子不可能竖直。所以球与斜面间没有弹力
弹力有无的判断
光滑球静止在水平地面
假设球与木块间有弹力
以球为研究对象,球受力:
G
N
N木块→球
球不可能静止,所以球与斜面间没有弹力
例:画出下列物体所受到的所有弹力。
水平面上的球
弹力的作用点和大小
1、弹力的作用点:两物体接触处,在受力物体上。
2、对于同一物体,弹力大小同形变大小有关。
利用力的平衡来计算
利用牛顿第二定律
弹簧弹力大小计算——
胡克定律
两个物体A和B,质量分别为M和m,用跨过定滑轮的轻绳相连,A静止于水平地面上,如图3-2-8所示.不计摩擦,A对绳的作用力的大小与地面对A的作用力的大小分别为多少?
弹簧弹力方向又什么样的呢?
弹簧两端的弹力方向,与弹簧中心轴线重合,指向弹簧恢复原状方向.
实验目的
1、探究弹力与
的定量关系。
2、学会利用图象研究两个物理量之间的关系的方法。
实验原理
1、如图所示,弹簧在下端悬挂钩码时会伸长,平衡时弹簧产生的弹力与
大小相等。
2、用刻度尺测出弹簧在不同的钩码拉力下的伸长量x,建立坐标系,以纵坐标表示弹力大小F,以横坐标表示弹簧的伸长量x,在坐标系中描写实验所测得的各组(x,F)对应的点,用
的曲线连接起来,根据实验所得的图线,就可探知弹力大小与伸长量间的关系。
弹簧伸长
所挂钩码的重力
平滑
探究弹力与弹簧伸长量的关系
五、胡克定律:
实验器材
轻质弹簧(一根),钩码(一盒),刻度尺,铁架台,重垂线,坐标纸,三角板
实验步骤
1、如图所示,将铁架台放于桌面上(固定好),将弹簧的一端固定于铁架台的横梁上,在挨近弹簧处将刻度尺(最小分度为mm)固定于铁架台上,并用
检查刻度尺是否竖直。
重垂线
2、记下弹簧下端不挂钩码时所对应的刻度L0
3、在弹簧下端挂上一个钩码,待钩码静止后,记下弹簧下端所对应的刻度L1
4、用上面方法,记下弹簧下端挂2个、3个、4个…
…钩码时,弹簧下端所对应的刻度L2、L3、L4
…
…,并将所得数据记录在表格中
5、用xn=Ln-L0计算出弹簧挂1个、2个、3个…
…钩码时弹簧的伸长量,并根据当地重力加速度值g,计算出所挂钩码的总重力,这个总重力就等于
的大小,将所得数据填入表格。
弹簧弹力
6、根据所测数据在坐标纸上描点,最好以弹簧弹力为纵坐标,以弹簧的伸长量为横坐标。
7、按照图中各点的分布与走向,尝试作出一条平滑的曲线(包括直线)。所画的点不一定正好都在这条曲线上,但要注意使曲线两侧的点数大致相同。
8、以弹簧的伸长为自变量,写出曲线所代表的函数,首先尝试一次函数,如果不行,则考虑二次函数。
9、解释函数表达式中常数的物理意义。
实验现象及注意事项
1、随着所挂钩码数量的增多,弹簧会越来越长,实验时,弹簧下端所挂钩码不宜太多,以免超出弹簧的弹性限度。
2、在建立坐标系描点时,我们要探求的是弹簧的伸长量与弹力大小的关系,而不是弹簧的总长度。
3、实验中外力的大小(即钩码的重力)与弹力的大小是相等的。
4、测原长时必须把弹簧竖直挂起来
五、胡克定律:
实验:探究弹力和弹簧伸长的关系
1、内容:
弹簧发生弹性形变时,弹力的大小跟弹簧伸长(或缩短)的长度x成正比。
2、公式:
F
=
k
x
其中:k——弹簧的劲度系数
(与弹簧的丝的粗细、材料、弹簧的直径、绕法和长度等量有关)
单位:牛每米,
符号N/m
x——弹簧伸长(或缩短)的长度
例1、下列关于弹力的说法不正确是?
A、只要两个物体接触就一定能产生弹力
B、两个接触并发生弹性形变的物体一定产生弹力
C、压力、支持力、拉力都是弹力
D、压力、支持力的方向总是垂直于支持面
例2、关于胡克定律F=kx中的x,下列说法正确的是?
A、x是弹簧伸长后或压缩后的长度
B、x是弹簧原来的长度
C、x是弹簧变化(伸长或压缩)的长度
D、x是弹簧原长加后来的长度
A
C
如图3-2-5所示,为一轻质弹簧的长度L和弹力F大小的关系,试由图线确定:
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧长为0.2m时弹力的大小.
(1)10cm
(2)200N/m
(3)20N
GA=100N,GB=40N,弹簧的劲度系数为500N/m,不计绳重和摩擦,求:物体A对支持面的压力和弹簧的伸长量。
小结
一、弹力产生条件:
①
直接接触
②
发生弹性形变
二、弹力方向
1、压力和支持力:
方向都垂直于接触面指向被压或被支持的物体。
2、拉力:
绳的拉力沿着绳指向绳
收缩的方向
三、弹力大小:
1、弹簧弹力:胡克定律F
=
k
x
2、其它弹力:由物体受其它力和运动状态求解
如图所示,A、B是质量均为m的两条磁铁,C为木块,水平放置。静止时B对A的弹力为F1,C对B的弹力为F2,则:(
)
A、F1=mg,F2=2mg B、F1>mg,F2=2mg
C、F1<mg,F2=2mg
D、F1>mg,F2>2mg
N
S
N
S
A
B
C
B
两根长均为20cm的弹簧,劲度系数分别为k1=200N/m,k2=100N/m,弹簧k2固定在A上,弹簧k1固定在A、B上,B放在水平地面上,弹簧竖直,如图所示。已知A、B所受的重力都是4N,今在k2的端点P施加一个竖直向上的力,缓慢地向上拉,当P点向上升距离为多少
时,B和地面恰好接触而没有作用力。弹簧自重不计。
如图A、B两物体重力分别是GA=3N、GB=4N,A用悬绳挂在天花板上,B放在水平地面上,A、B间的轻弹簧的弹力F=2N,则绳中张力FT和B对地面的压力FN的可能值分别为
C、1N和6N
D、2N和5N
A、7N和0N
B、5N和2N
(
BC
)
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
