2011学年第一学期上海市长宁区高三教学质量检测数学试卷(文、理)
文档属性
| 名称 | 2011学年第一学期上海市长宁区高三教学质量检测数学试卷(文、理) |  | |
| 格式 | zip | ||
| 文件大小 | 190.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-07 09:35:11 | ||
图片预览




文档简介
长宁区2011学年第一学期高三教学质量检测
数学试卷(文、理)
考生注意:本试卷共有23道试题,满分150分.考试时间120分钟.解答必须写在答题纸上的规定区域,写在试卷或草稿纸上的答案一律不予评分.
一.填空题(本大题满分56分)本大题共有14题,考生应在答题纸的相应编号的空格内填写结果,每题填对得4分,否则一律得零分.
1.不等式的解集是.
2.行列式中的代数余子式的值为.
3.从总体中抽取一个样本是5,6,7,8,9,则该样本的方差是 .
4.等比数列的首项与公比分别是复数(是虚数单位的实部与虚部,
则数列的各项和的值为 。
5. 随机抽取10个同学中至少有2个同学在同一月份生日的概率为
(精确到0.001).
6.(文)中,为所对的边,且,则
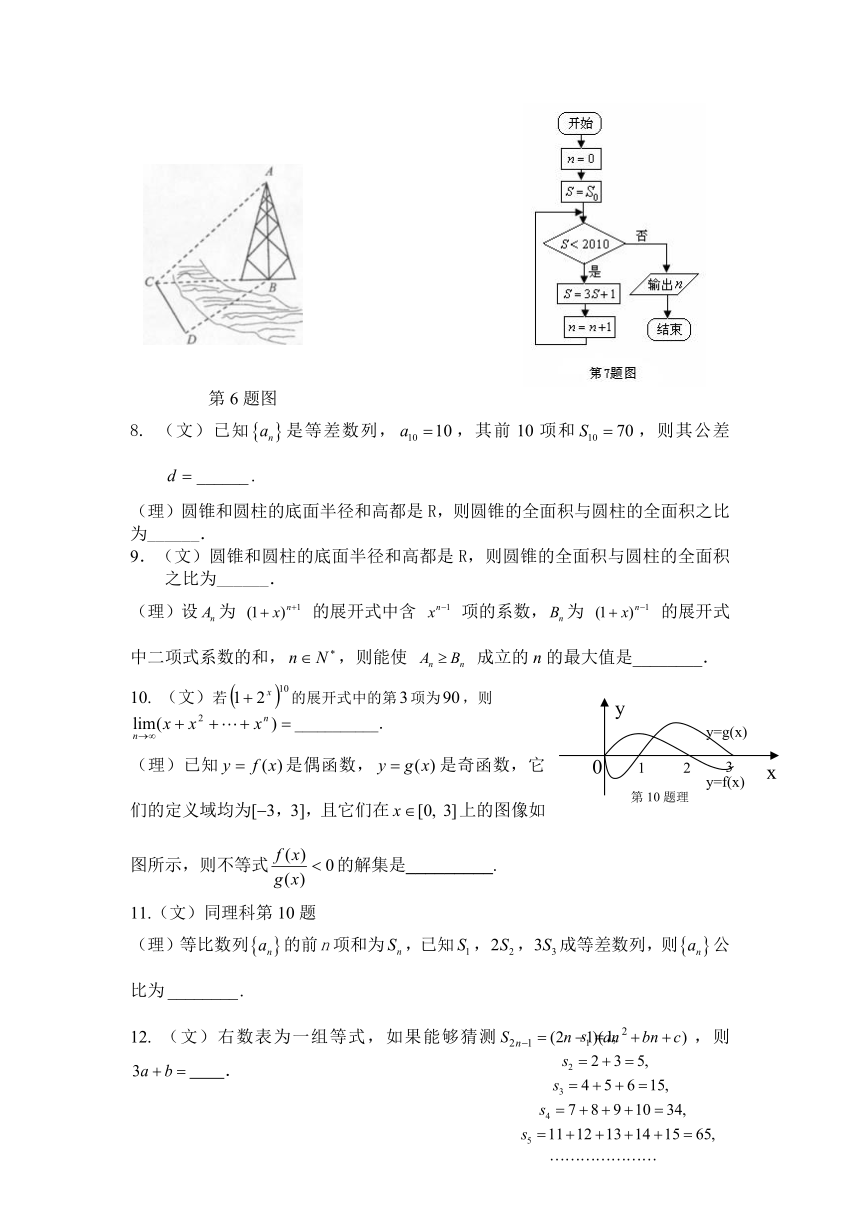
(理)如图,测量河对岸的塔高时,可以选与塔底在同一水平面内的两个测点与,测得.,米,并在点测得塔顶的仰角为,则塔高=_________.
7.某程序框图如图所示,该程序运行后输出的n值是8,则从集合中所有满足条件的S0值为
第6题图
8. (文)已知是等差数列,,其前10项和,则其公差
(理)圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为______.
9.(文)圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为______.
(理)设为 的展开式中含 项的系数,为 的展开式中二项式系数的和,,则能使 成立的n的最大值是________.
10. (文)若的展开式中的第项为,则___________.
(理)已知是偶函数,是奇函数,它们的定义域均为[3,3],且它们在上的图像如图所示,则不等式的解集是_________.
11.(文)同理科第10题
(理)等比数列的前项和为,已知,,成等差数列,则公比为
12. (文)右数表为一组等式,如果能够猜测,则 .
(理),,,则的
最小值是 .
13.已知函数 的定义域为R,且对任意
,都有。
若,,则 .
14.(文)已知函数 的定义域为R,且对任意 ,都有。若,,则 .
(理)把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列,若,则__________.
二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,每题选对得5分,否则一律得零分.
15.下列命题正确的是 ( )
A.若,则且
B.中,是的充要条件
C.若,则
D.命题“若,则”的否命题是“若,则”
16.已知平面向量=(1,-3),=(4,-2),与垂直,则是( )
A. 1 B. 2 C. -2 D. -1
17.下列命题中 ( )
① 三点确定一个平面;
② 若一条直线垂直于平面内的无数条直线,则该直线与平面垂直;
③ 同时垂直于一条直线的两条直线平行;
④ 底面边长为2,侧棱长为的正四棱锥的表面积为12.
正确的个数为 ( )
A. 0 B. 1 C. 2 D. 3
18.已知,为的反函数.若,那么与在同一坐标系内的图像可能是 ( )
A B C D
三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸的相应编号规定区域内写出必须的步骤.
19.(本题满分12分)
设(其中是虚数单位)是实系数方程的一个根,求的值.
20.(本题满分12分)本题共有2个小题,第1小题满分8分,第2小题满分4分.
在正四棱柱中,已知底面的边长为2,点P是的中点,直线AP与平面成角.
(文)(1)求的长;
(2)求异面直线和AP所成角的大小.(结果用
反三角函数值表示);
(理)(1)求异面直线和AP所成角的大小.(结果用
反三角函数值表示) ;
(2)求点到平面的距离.
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知为锐角,且.
(1)设,若,求的值;
(2)在中,若,,,求的面积.
22.(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数是定义域为R的奇函数.
(1)求k值;
(2)(文)当时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式恒成立的的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
23.(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列中,
(1)求证数列不是等比数列,并求该数列的通项公式;
(2)求数列的前项和;
(3)设数列的前项和为,若对任意恒成立,求的最小值.
(理)对数列和,若对任意正整数,恒有,则称数列是数列的“下界数列”.
(1)设数列,请写出一个公比不为1的等比数列,使数列是数列的“下界数列”;
(2)设数列,求证数列是数列的“下界数列”;
(3)设数列,构造,,求使对恒成立的的最小值.
长宁区2011学年第一学期高三教学质量检测
数学试卷评分标准
填空题(每小题4分,一共56分)
题号 1 2 3 4 5 6 7
答案 2 3 (文)(理) 0
8 9 10 11 12 13 14
(文)(理) (文)(理)4 (文)1(理) (文)(理) (文)4(理) (文)(理) (文)(理)1028
选择题(每小题5分,一共20分)
题号 15 16 17 18
答案 B D B C
解答题
19、(本题满分12分)
解:………………2分
, ………………4分
因此解得,………………6分
又解得,………………8分
因此,………………12分
20、(本题满分12分)
(文)解: (1)连结BP,设长方体的高为h ,因为AB⊥平面 ,
所以,∠APB即为直线AP与平面所成的角。 …………………………3分
,由得.……………………6分
(2)又因为,
所以是异面直线和AP所成的角. ………………………………8分
在中,,,,…………………10分
所以,,即……………12分
(理)解: (1)连结BP,设长方体的高为h ,
因为AB⊥平面 ,所以,∠APB即为直线AP与平面所成的角。 …………………………2分
,由得.…………………4分
又因为,所以是异面直线和AP所成的角. ………………………………5分
在中,,,,…………………6分
所以,,即……………8分
(2)设点到平面的距离为,,
, ……………10分
由,得,
。 ……………12分
21、(本题满分14分)
(1)
……………2分
又∵为锐角
, ,……………4分
, ……………6分
(2)由(1)得A=,而,
根据正弦定理得, ……………8分
求得 ……………10分
, ……………12分
从而求得的面积。………14分
22、(本题满分18分)
解(1)∵f(x)是定义域为R的奇函数,
∴f(0)=0, …………………… 2分
∴1-(k-1)=0,∴k=2, …………………… 4分
(2)(文)
,单调递减,单调递增,故f(x)在R上单调递减。
…………………… 6分
原不等式化为:f(x2+2x)>f(4-x)
∴x2+2x<4-x,即x2+3x-4<0 …………………… 8分
∴,
∴不等式的解集为{x|}. …………………………10分
(2)(理)
………………6分
单调递减,单调递增,故f(x)在R上单调递减。 ………………7分
不等式化为
恒成立,…………… 8分
,解得。…………………… 10分
(3)∵f(1)=,,即
……………………………………12分
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,
由(1)可知f(x)=2x-2-x为增函数
∵x≥1,∴t≥f(1)=,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥)………………15分
若m≥,当t=m时,h(t)min=2-m2=-2,∴m=2………… 16分
若m<,当t=时,h(t)min=-3m=-2,解得m=>,舍去……17分
综上可知m=2. ………………………………18分
23、(本题满分18分)
(文)(1),不是等比数列;………2分
,及成等比数列,
公比为2, ……………6分
(2),
当为偶数时,
;……………8分
当为奇数时,
.……………10分
因此,……………12分
(3)
。 ……………13分
, ……………14分
因此不等式为 3(1-k2)3(-1)2,
k,即k-(2-1),
……………16分
F(n)=-(2-1)单调递减;F(1)= 最大,
,即的最小值为。……………18分
(理)
(1)等,答案不唯一;……………4分
(2),当时最小值为9,;……………6分
,则,
因此,时,最大值为6,……………9分
所以,,数列是数列的“下界数列”;……………10分
(3),…11分
, ……………12分
不等式为,,,…13分
设,则,…………15分
当时,单调递增,时,取得最小值,因此, ……………17分
的最小值为 ……………18分
x
0
y
1
2
3
y=f(x)
y=g(x)
第10题理
数学试卷(文、理)
考生注意:本试卷共有23道试题,满分150分.考试时间120分钟.解答必须写在答题纸上的规定区域,写在试卷或草稿纸上的答案一律不予评分.
一.填空题(本大题满分56分)本大题共有14题,考生应在答题纸的相应编号的空格内填写结果,每题填对得4分,否则一律得零分.
1.不等式的解集是.
2.行列式中的代数余子式的值为.
3.从总体中抽取一个样本是5,6,7,8,9,则该样本的方差是 .
4.等比数列的首项与公比分别是复数(是虚数单位的实部与虚部,
则数列的各项和的值为 。
5. 随机抽取10个同学中至少有2个同学在同一月份生日的概率为
(精确到0.001).
6.(文)中,为所对的边,且,则
(理)如图,测量河对岸的塔高时,可以选与塔底在同一水平面内的两个测点与,测得.,米,并在点测得塔顶的仰角为,则塔高=_________.
7.某程序框图如图所示,该程序运行后输出的n值是8,则从集合中所有满足条件的S0值为
第6题图
8. (文)已知是等差数列,,其前10项和,则其公差
(理)圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为______.
9.(文)圆锥和圆柱的底面半径和高都是R,则圆锥的全面积与圆柱的全面积之比为______.
(理)设为 的展开式中含 项的系数,为 的展开式中二项式系数的和,,则能使 成立的n的最大值是________.
10. (文)若的展开式中的第项为,则___________.
(理)已知是偶函数,是奇函数,它们的定义域均为[3,3],且它们在上的图像如图所示,则不等式的解集是_________.
11.(文)同理科第10题
(理)等比数列的前项和为,已知,,成等差数列,则公比为
12. (文)右数表为一组等式,如果能够猜测,则 .
(理),,,则的
最小值是 .
13.已知函数 的定义域为R,且对任意
,都有。
若,,则 .
14.(文)已知函数 的定义域为R,且对任意 ,都有。若,,则 .
(理)把正整数排列成如图甲三角形数阵,然后擦去第偶数行中的奇数和第奇数行中的偶数,得到如图乙的三角形数阵,再把图乙中的数按从小到大的顺序排成一列,得到一个数列,若,则__________.
二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,每题选对得5分,否则一律得零分.
15.下列命题正确的是 ( )
A.若,则且
B.中,是的充要条件
C.若,则
D.命题“若,则”的否命题是“若,则”
16.已知平面向量=(1,-3),=(4,-2),与垂直,则是( )
A. 1 B. 2 C. -2 D. -1
17.下列命题中 ( )
① 三点确定一个平面;
② 若一条直线垂直于平面内的无数条直线,则该直线与平面垂直;
③ 同时垂直于一条直线的两条直线平行;
④ 底面边长为2,侧棱长为的正四棱锥的表面积为12.
正确的个数为 ( )
A. 0 B. 1 C. 2 D. 3
18.已知,为的反函数.若,那么与在同一坐标系内的图像可能是 ( )
A B C D
三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸的相应编号规定区域内写出必须的步骤.
19.(本题满分12分)
设(其中是虚数单位)是实系数方程的一个根,求的值.
20.(本题满分12分)本题共有2个小题,第1小题满分8分,第2小题满分4分.
在正四棱柱中,已知底面的边长为2,点P是的中点,直线AP与平面成角.
(文)(1)求的长;
(2)求异面直线和AP所成角的大小.(结果用
反三角函数值表示);
(理)(1)求异面直线和AP所成角的大小.(结果用
反三角函数值表示) ;
(2)求点到平面的距离.
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知为锐角,且.
(1)设,若,求的值;
(2)在中,若,,,求的面积.
22.(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数是定义域为R的奇函数.
(1)求k值;
(2)(文)当时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式恒成立的的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.
23.(本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)已知数列中,
(1)求证数列不是等比数列,并求该数列的通项公式;
(2)求数列的前项和;
(3)设数列的前项和为,若对任意恒成立,求的最小值.
(理)对数列和,若对任意正整数,恒有,则称数列是数列的“下界数列”.
(1)设数列,请写出一个公比不为1的等比数列,使数列是数列的“下界数列”;
(2)设数列,求证数列是数列的“下界数列”;
(3)设数列,构造,,求使对恒成立的的最小值.
长宁区2011学年第一学期高三教学质量检测
数学试卷评分标准
填空题(每小题4分,一共56分)
题号 1 2 3 4 5 6 7
答案 2 3 (文)(理) 0
8 9 10 11 12 13 14
(文)(理) (文)(理)4 (文)1(理) (文)(理) (文)4(理) (文)(理) (文)(理)1028
选择题(每小题5分,一共20分)
题号 15 16 17 18
答案 B D B C
解答题
19、(本题满分12分)
解:………………2分
, ………………4分
因此解得,………………6分
又解得,………………8分
因此,………………12分
20、(本题满分12分)
(文)解: (1)连结BP,设长方体的高为h ,因为AB⊥平面 ,
所以,∠APB即为直线AP与平面所成的角。 …………………………3分
,由得.……………………6分
(2)又因为,
所以是异面直线和AP所成的角. ………………………………8分
在中,,,,…………………10分
所以,,即……………12分
(理)解: (1)连结BP,设长方体的高为h ,
因为AB⊥平面 ,所以,∠APB即为直线AP与平面所成的角。 …………………………2分
,由得.…………………4分
又因为,所以是异面直线和AP所成的角. ………………………………5分
在中,,,,…………………6分
所以,,即……………8分
(2)设点到平面的距离为,,
, ……………10分
由,得,
。 ……………12分
21、(本题满分14分)
(1)
……………2分
又∵为锐角
, ,……………4分
, ……………6分
(2)由(1)得A=,而,
根据正弦定理得, ……………8分
求得 ……………10分
, ……………12分
从而求得的面积。………14分
22、(本题满分18分)
解(1)∵f(x)是定义域为R的奇函数,
∴f(0)=0, …………………… 2分
∴1-(k-1)=0,∴k=2, …………………… 4分
(2)(文)
,单调递减,单调递增,故f(x)在R上单调递减。
…………………… 6分
原不等式化为:f(x2+2x)>f(4-x)
∴x2+2x<4-x,即x2+3x-4<0 …………………… 8分
∴,
∴不等式的解集为{x|}. …………………………10分
(2)(理)
………………6分
单调递减,单调递增,故f(x)在R上单调递减。 ………………7分
不等式化为
恒成立,…………… 8分
,解得。…………………… 10分
(3)∵f(1)=,,即
……………………………………12分
∴g(x)=22x+2-2x-2m(2x-2-x)=(2x-2-x)2-2m(2x-2-x)+2.
令t=f(x)=2x-2-x,
由(1)可知f(x)=2x-2-x为增函数
∵x≥1,∴t≥f(1)=,
令h(t)=t2-2mt+2=(t-m)2+2-m2 (t≥)………………15分
若m≥,当t=m时,h(t)min=2-m2=-2,∴m=2………… 16分
若m<,当t=时,h(t)min=-3m=-2,解得m=>,舍去……17分
综上可知m=2. ………………………………18分
23、(本题满分18分)
(文)(1),不是等比数列;………2分
,及成等比数列,
公比为2, ……………6分
(2),
当为偶数时,
;……………8分
当为奇数时,
.……………10分
因此,……………12分
(3)
。 ……………13分
, ……………14分
因此不等式为 3(1-k2)3(-1)2,
k,即k-(2-1),
……………16分
F(n)=-(2-1)单调递减;F(1)= 最大,
,即的最小值为。……………18分
(理)
(1)等,答案不唯一;……………4分
(2),当时最小值为9,;……………6分
,则,
因此,时,最大值为6,……………9分
所以,,数列是数列的“下界数列”;……………10分
(3),…11分
, ……………12分
不等式为,,,…13分
设,则,…………15分
当时,单调递增,时,取得最小值,因此, ……………17分
的最小值为 ……………18分
x
0
y
1
2
3
y=f(x)
y=g(x)
第10题理
同课章节目录
