6.3向心加速度 20张PPT
文档属性
| 名称 | 6.3向心加速度 20张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-08 00:00:00 | ||
图片预览






文档简介
第六章 圆周运动
6.3 向心加速度
如何确定天宫二号空间实验室在轨飞行时加速度的方向和大小呢?
教学目标
1.理解向心加速度的概念。
2.知道向心加速度和线速度、角速度的关系式。
3.能够运用向心加速度公式求解有关问题。
新课导入
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。
尽管线速度大小不变,但方向
却时刻变化,因此,它运动的
加速度一定不为0。那么,该如
何确定它在轨飞行时加速度的方
向和大小呢?
匀速圆周运动的加速度方向
物体做匀速圆周运动时,所受合力提供向心力,合力的方向总是指向圆心,如图 6.3-1 所示。根据牛顿第二定律,物体运动的加速度方向与它所受合力的方向相同。
定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
物理意义:描述线速度改变的快慢,只改变线速度方向,不改变其大小。
方向:总是沿着圆周运动的半径指向圆心,即方向始终与运动方向垂直,方向时刻改变。不论加速度an的大小是否变化,an的方向总是时刻改变的,所以圆周运动一定是变加速运动。
1.向心加速度
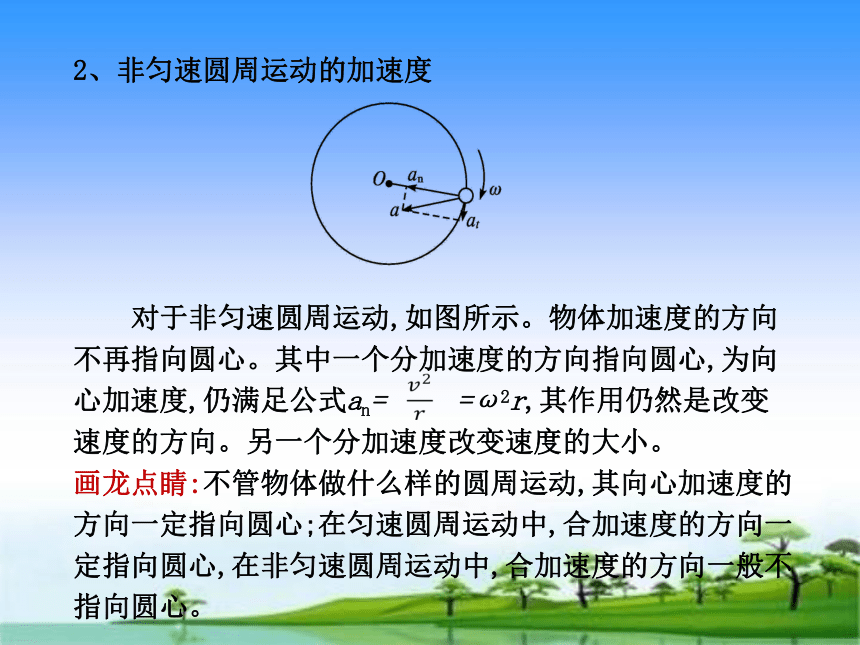
2、非匀速圆周运动的加速度
对于非匀速圆周运动,如图所示。物体加速度的方向不再指向圆心。其中一个分加速度的方向指向圆心,为向心加速度,仍满足公式an= =ω2r,其作用仍然是改变速度的方向。另一个分加速度改变速度的大小。
画龙点睛:不管物体做什么样的圆周运动,其向心加速度的方向一定指向圆心;在匀速圆周运动中,合加速度的方向一定指向圆心,在非匀速圆周运动中,合加速度的方向一般不指向圆心。
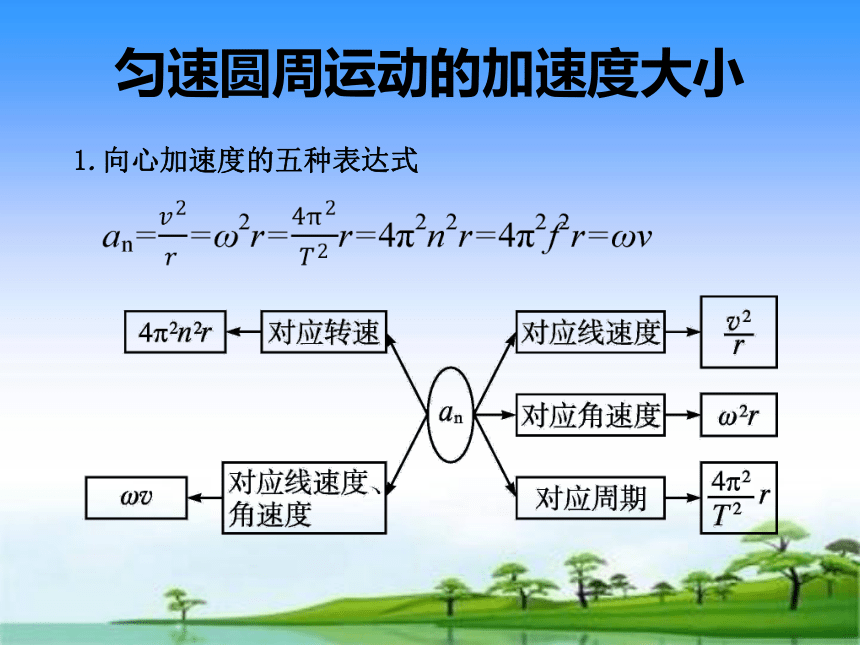
1.向心加速度的五种表达式
匀速圆周运动的加速度大小
2.公式推导:
法一:牛顿第二定律
已知向心力表达式:Fn= m ,Fn=mω2r。
(1)根据牛顿第二定律Fn=man得到向心加速度的基本表达式:an= ,an=ω2r;
(2)由于v=ωr,所以向心加速度也可以写成an=ωv;
(3)由于ω= =2πf,所以向心加速度也可以写成
an= r=4π2f2r。
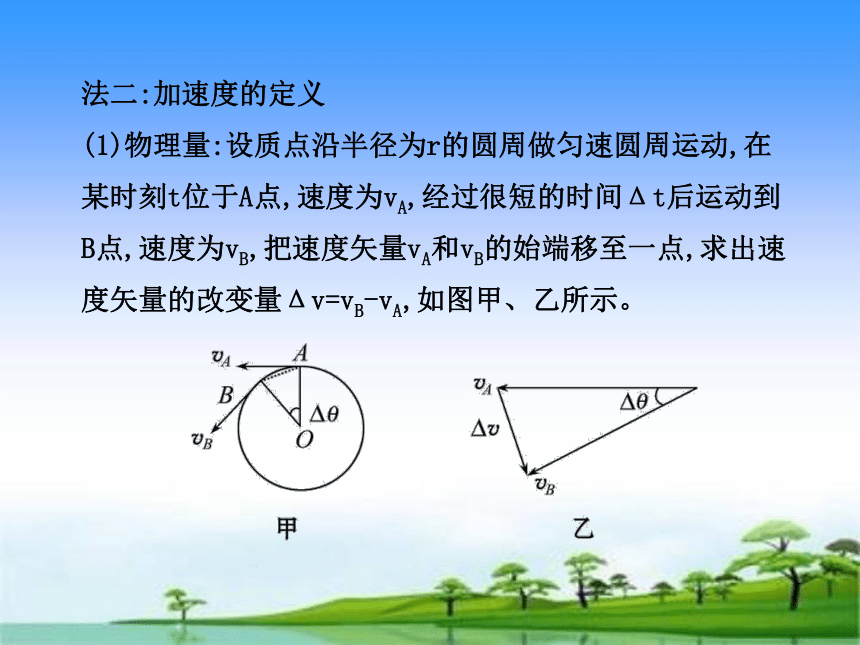
法二:加速度的定义
(1)物理量:设质点沿半径为r的圆周做匀速圆周运动,在某时刻t位于A点,速度为vA,经过很短的时间Δt后运动到B点,速度为vB,把速度矢量vA和vB的始端移至一点,求出速度矢量的改变量Δv=vB-vA,如图甲、乙所示。
(2)推导过程:图乙中的矢量三角形与图甲中的△OAB是相似三角形,用v表示vA和vB的大小,用Δl表示弦AB的长度,则有:????????? =???????????,故Δv= ?????????v。
所以加速度an= ??????????=?????????????? 。
而当Δt趋近于零时,?????????? 表示线速度的大小v,于是得到an= ???????????? 。再由v=rω得an=ω2r。
?
3.向心加速度与半径的关系:
从公式 看,线速度一定时,向心加速度与圆周运动的半径成反比;从公式 an=ω2r 看,角速度一定时,向心加速度与半径成正比。
自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点 A、B、C,如图
6.3-2 所示。其中哪两点向心加
速度的关系适用于“向心加速度
与半径成正比”,哪两点适用于
“向心加速度与半径成反比”?
给出解释。
思考与讨论
1、 B、C两点在同一轮上,同轴传动时,这两点的角速度相同,由公式
2、 A、B两点在同一个链条上,两点的线速度大小相同,由
an =
v2
r
an = ω2r
知ω一定时,向心加速度与半径成正比。
o
r
ω一定
v一定
a
知v一定时,向心加速度与半径成反比。
例:如图6.3-3所示,在长为l的细绳下端拴一个质量为m的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这
样就成了一个圆锥摆。当绳子跟
竖直方向的夹角为θ时,小球运
动的向心加速度an的大小为多
少?通过计算说明:要增大夹角θ,
应该增大小球运动的角速度。
θ
r
O
G
Fn
F
解 根据对小球的受力分析,可得小球的向心力
Fn=mgtanθ
根据牛顿第二定律可得小球运动向心加速度
an=
=gtanθ
根据几何关系可知小球圆周运动半径
r=lsinθ
又an=ω2r,得cosθ=
从此式可以看出,当小球运动角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
1.如图所示,质量为m的木块从半径为R的半球形碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使木块的速率不变,那么 ( )
A.加速度为零
B.加速度恒定
C.加速度大小不变,方向时刻改变,但不一定指向圆心
D.加速度大小不变,方向时刻指向圆心
解析:由题意知,木块做匀速圆周运动,木块的加速度大小不变,方向时刻指向圆心,D正确,A、B、C错误。
D
随堂练习
2、如图所示,一个大轮通过皮带拉着小轮转动,皮带和两轮之间无滑动,大轮的半径是小轮的2倍,大轮上的一点S与转轴的距离是半径的13。当大轮边缘上P点的向心加速度是12 m/s2时,大轮上的S点和小轮边缘上的Q点的向心加速度各为多大?
思路引导:先根据皮带传动或同轴转动分析出研究点的线速度关系或角速度关系,然后再利用向心加速度公式分析。
答案:aS=4 m/s2 aQ=24 m/s2
课堂小结
6.3 向心加速度
如何确定天宫二号空间实验室在轨飞行时加速度的方向和大小呢?
教学目标
1.理解向心加速度的概念。
2.知道向心加速度和线速度、角速度的关系式。
3.能够运用向心加速度公式求解有关问题。
新课导入
天宫二号空间实验室在轨飞行时,可认为它绕地球做匀速圆周运动。
尽管线速度大小不变,但方向
却时刻变化,因此,它运动的
加速度一定不为0。那么,该如
何确定它在轨飞行时加速度的方
向和大小呢?
匀速圆周运动的加速度方向
物体做匀速圆周运动时,所受合力提供向心力,合力的方向总是指向圆心,如图 6.3-1 所示。根据牛顿第二定律,物体运动的加速度方向与它所受合力的方向相同。
定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度
物理意义:描述线速度改变的快慢,只改变线速度方向,不改变其大小。
方向:总是沿着圆周运动的半径指向圆心,即方向始终与运动方向垂直,方向时刻改变。不论加速度an的大小是否变化,an的方向总是时刻改变的,所以圆周运动一定是变加速运动。
1.向心加速度
2、非匀速圆周运动的加速度
对于非匀速圆周运动,如图所示。物体加速度的方向不再指向圆心。其中一个分加速度的方向指向圆心,为向心加速度,仍满足公式an= =ω2r,其作用仍然是改变速度的方向。另一个分加速度改变速度的大小。
画龙点睛:不管物体做什么样的圆周运动,其向心加速度的方向一定指向圆心;在匀速圆周运动中,合加速度的方向一定指向圆心,在非匀速圆周运动中,合加速度的方向一般不指向圆心。
1.向心加速度的五种表达式
匀速圆周运动的加速度大小
2.公式推导:
法一:牛顿第二定律
已知向心力表达式:Fn= m ,Fn=mω2r。
(1)根据牛顿第二定律Fn=man得到向心加速度的基本表达式:an= ,an=ω2r;
(2)由于v=ωr,所以向心加速度也可以写成an=ωv;
(3)由于ω= =2πf,所以向心加速度也可以写成
an= r=4π2f2r。
法二:加速度的定义
(1)物理量:设质点沿半径为r的圆周做匀速圆周运动,在某时刻t位于A点,速度为vA,经过很短的时间Δt后运动到B点,速度为vB,把速度矢量vA和vB的始端移至一点,求出速度矢量的改变量Δv=vB-vA,如图甲、乙所示。
(2)推导过程:图乙中的矢量三角形与图甲中的△OAB是相似三角形,用v表示vA和vB的大小,用Δl表示弦AB的长度,则有:????????? =???????????,故Δv= ?????????v。
所以加速度an= ??????????=?????????????? 。
而当Δt趋近于零时,?????????? 表示线速度的大小v,于是得到an= ???????????? 。再由v=rω得an=ω2r。
?
3.向心加速度与半径的关系:
从公式 看,线速度一定时,向心加速度与圆周运动的半径成反比;从公式 an=ω2r 看,角速度一定时,向心加速度与半径成正比。
自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点 A、B、C,如图
6.3-2 所示。其中哪两点向心加
速度的关系适用于“向心加速度
与半径成正比”,哪两点适用于
“向心加速度与半径成反比”?
给出解释。
思考与讨论
1、 B、C两点在同一轮上,同轴传动时,这两点的角速度相同,由公式
2、 A、B两点在同一个链条上,两点的线速度大小相同,由
an =
v2
r
an = ω2r
知ω一定时,向心加速度与半径成正比。
o
r
ω一定
v一定
a
知v一定时,向心加速度与半径成反比。
例:如图6.3-3所示,在长为l的细绳下端拴一个质量为m的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这
样就成了一个圆锥摆。当绳子跟
竖直方向的夹角为θ时,小球运
动的向心加速度an的大小为多
少?通过计算说明:要增大夹角θ,
应该增大小球运动的角速度。
θ
r
O
G
Fn
F
解 根据对小球的受力分析,可得小球的向心力
Fn=mgtanθ
根据牛顿第二定律可得小球运动向心加速度
an=
=gtanθ
根据几何关系可知小球圆周运动半径
r=lsinθ
又an=ω2r,得cosθ=
从此式可以看出,当小球运动角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
1.如图所示,质量为m的木块从半径为R的半球形碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使木块的速率不变,那么 ( )
A.加速度为零
B.加速度恒定
C.加速度大小不变,方向时刻改变,但不一定指向圆心
D.加速度大小不变,方向时刻指向圆心
解析:由题意知,木块做匀速圆周运动,木块的加速度大小不变,方向时刻指向圆心,D正确,A、B、C错误。
D
随堂练习
2、如图所示,一个大轮通过皮带拉着小轮转动,皮带和两轮之间无滑动,大轮的半径是小轮的2倍,大轮上的一点S与转轴的距离是半径的13。当大轮边缘上P点的向心加速度是12 m/s2时,大轮上的S点和小轮边缘上的Q点的向心加速度各为多大?
思路引导:先根据皮带传动或同轴转动分析出研究点的线速度关系或角速度关系,然后再利用向心加速度公式分析。
答案:aS=4 m/s2 aQ=24 m/s2
课堂小结
