2020-2021学年高一数学人教A版必修4第一章1.4.2 正弦函数、余弦函数的性质 课件(共16张PPT)
文档属性
| 名称 | 2020-2021学年高一数学人教A版必修4第一章1.4.2 正弦函数、余弦函数的性质 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 890.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
1.4.2
正、余弦函数的性质(二)
学习目标:
【基础目标】借助图象理解正弦函数、余弦函数的基本性质.
【提高目标】求复合函数的单调区间,体会数形结合思想及整体换元思想.
重点:通过正弦函数、余弦函数的图象归纳其性质.
难点:整体换元思想的渗透,复合函数单调性的求法.
整体感知,明标定径
____
____
____
_______
____
_______
____
____
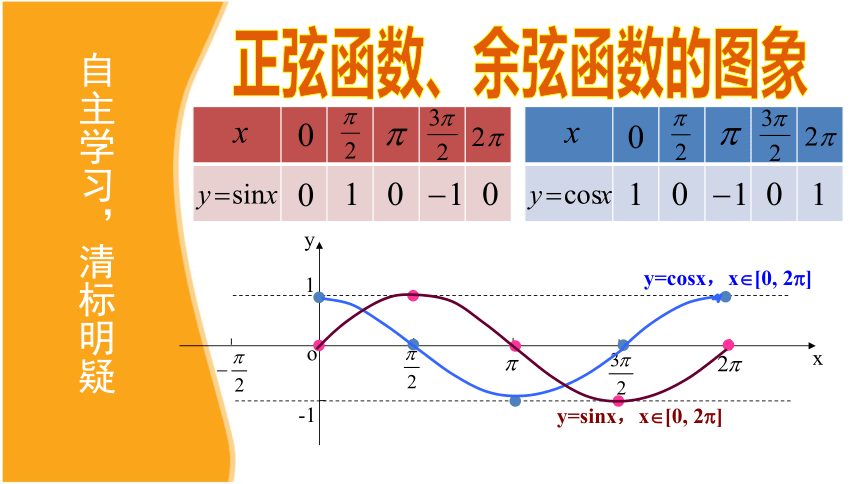
自主学习,清标明疑
y
x
o
1
-1
y=sinx,x?[0,
2?]
y=cosx,x?[0,
2?]
正弦函数、余弦函数的图象
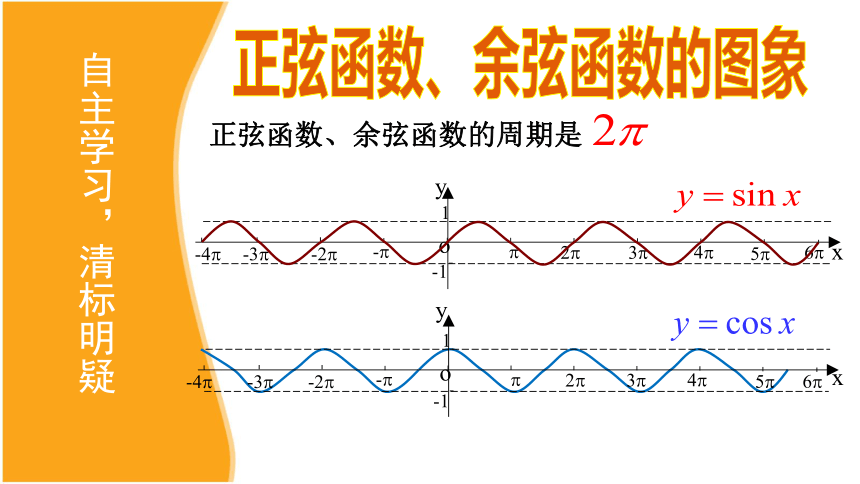
自主学习,清标明疑
正弦函数、余弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
x
6?
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
正弦函数、余弦函数的周期是
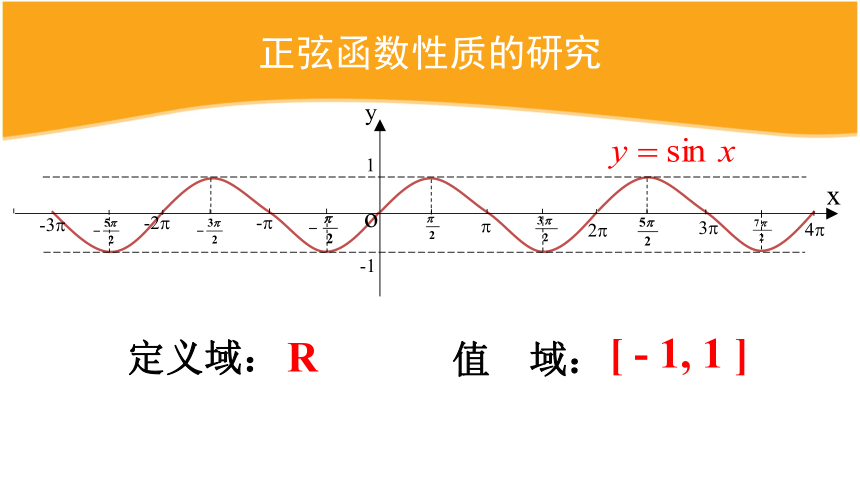
正弦函数性质的研究
定义域:
R
值
域:
[
-
1,
1
]
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
正弦函数性质的研究
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
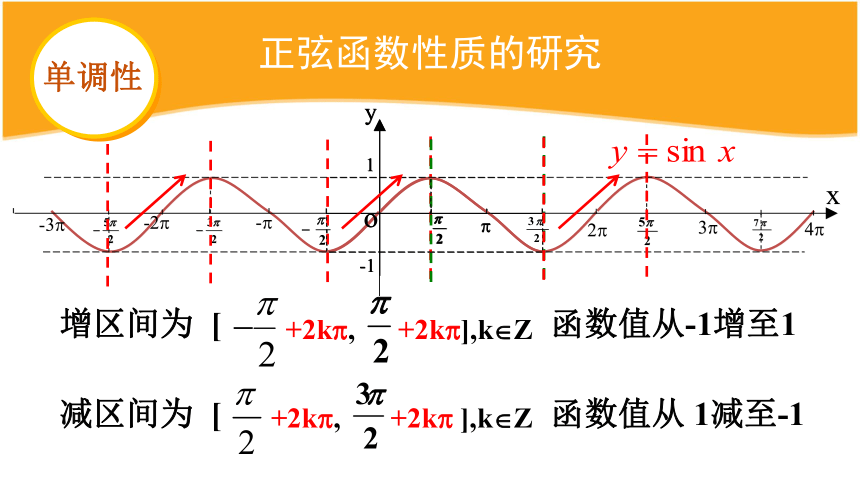
增区间为
[
,
]
函数值从-1增至1
减区间为
[
,
]
函数值从
1减至-1
+2k?,
+2k?],k?Z
+2k?,
+2k?
],k?Z
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
单调性
正弦函数性质的研究
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
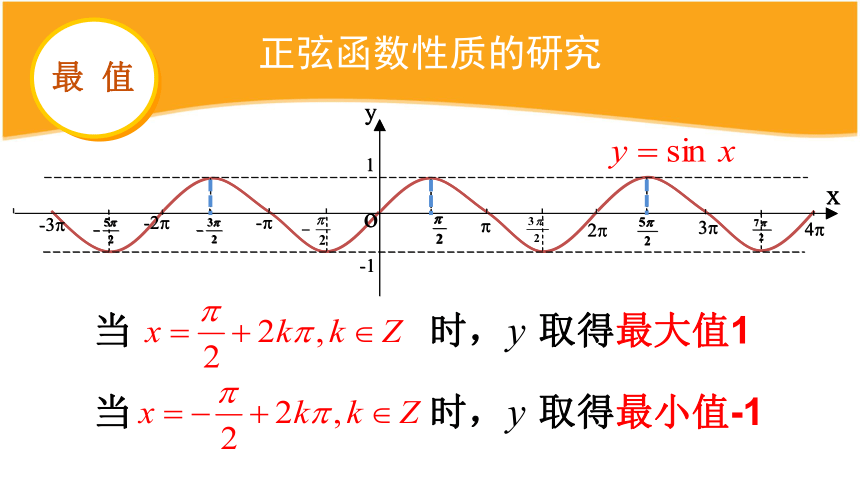
当
时,
取得最大值1
当
时,
取得最小值-1
最
值
正弦函数性质的研究
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
图象关于原点对称
【奇函数】
奇偶性
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
正弦函数性质的研究
对称轴:
对称中心:
对称性
交流思辨,释疑解惑
定义域:
R
值
域:
[
-
1,
1
]
增区间:
减区间:
奇偶性:
对称轴:
对称中心:
最
值:
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
小组讨论:
余弦函数的性质
典例分析
【例1】求函数
的最值,并写出取得最大值、最小值时自变量
的集合.
t
典例分析
【例2】求函数
的单调递增区间.
【例2】求函数
的单调递增区间.
【变式1】求函数
,
的单调递增区间.
【变式2】求函数
的单调递增区间.
梳理归纳,筑构建模
学到了哪些数学知识?
掌握了哪些数学方法?
定义域
值
域
单调性
增区间
减区间
最值
奇偶性
对称轴
对称中心
梳理归纳,筑构建模
R
R
[
-
1,
1
]
[
-
1,
1
]
偶函数
奇函数
课后作业
A级:教材P46-A组第5题
B级:求函数
的单调递增区间.
拾遗巩固,拓展提升
1.4.2
正、余弦函数的性质(二)
学习目标:
【基础目标】借助图象理解正弦函数、余弦函数的基本性质.
【提高目标】求复合函数的单调区间,体会数形结合思想及整体换元思想.
重点:通过正弦函数、余弦函数的图象归纳其性质.
难点:整体换元思想的渗透,复合函数单调性的求法.
整体感知,明标定径
____
____
____
_______
____
_______
____
____
自主学习,清标明疑
y
x
o
1
-1
y=sinx,x?[0,
2?]
y=cosx,x?[0,
2?]
正弦函数、余弦函数的图象
自主学习,清标明疑
正弦函数、余弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
x
6?
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y
正弦函数、余弦函数的周期是
正弦函数性质的研究
定义域:
R
值
域:
[
-
1,
1
]
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
正弦函数性质的研究
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
增区间为
[
,
]
函数值从-1增至1
减区间为
[
,
]
函数值从
1减至-1
+2k?,
+2k?],k?Z
+2k?,
+2k?
],k?Z
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
单调性
正弦函数性质的研究
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
当
时,
取得最大值1
当
时,
取得最小值-1
最
值
正弦函数性质的研究
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
图象关于原点对称
【奇函数】
奇偶性
x
y
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
正弦函数性质的研究
对称轴:
对称中心:
对称性
交流思辨,释疑解惑
定义域:
R
值
域:
[
-
1,
1
]
增区间:
减区间:
奇偶性:
对称轴:
对称中心:
最
值:
y
x
o
-?
-1
2?
3?
4?
-2?
-3?
1
?
小组讨论:
余弦函数的性质
典例分析
【例1】求函数
的最值,并写出取得最大值、最小值时自变量
的集合.
t
典例分析
【例2】求函数
的单调递增区间.
【例2】求函数
的单调递增区间.
【变式1】求函数
,
的单调递增区间.
【变式2】求函数
的单调递增区间.
梳理归纳,筑构建模
学到了哪些数学知识?
掌握了哪些数学方法?
定义域
值
域
单调性
增区间
减区间
最值
奇偶性
对称轴
对称中心
梳理归纳,筑构建模
R
R
[
-
1,
1
]
[
-
1,
1
]
偶函数
奇函数
课后作业
A级:教材P46-A组第5题
B级:求函数
的单调递增区间.
拾遗巩固,拓展提升
