2020-2021学年高一下学期数学人教A版必修4第一章1.4.1 正弦函数、余弦函数的图象 教案Word
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版必修4第一章1.4.1 正弦函数、余弦函数的图象 教案Word |  | |
| 格式 | zip | ||
| 文件大小 | 574.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 11:13:03 | ||
图片预览



文档简介
人
教
A
版
数
学
必
修4
P30—34
1.4.1?
正弦函数、余弦函数的图象
(一)教学具准备
直尺、圆规、投影仪.
(二)教学目标
1.了解作正、余弦函数图象的转化过程.
2.掌握五点作图法,并会用此方法作出
上的正弦曲线、余弦曲线.
3.体会转化与化归思想在本节课的应用.
(三)教学设计的基本构想
通过诱导公式对正弦函数基本性质进行研究,利用转化与化归的数学思想方法,将问题由大变小,逐步降低研究问题的难度,达到本节课给出正余弦函数的目的.具体流程如下:
(四)教学过程
1.设置情境
引进弧度制以后,
就可以看做是定义域为R
的实变量函数.作为函数,我们首先要关注其图像特征.本节课我们一起来学习作正、余弦函数图像的方法.
2.探索研究
(1)复习诱导公式
前面我们已经学习过三角函数的诱导公式,即将
的三角函数化为角的某种三角函数值的方法,请同学们回顾:
一、奇变偶不变、符号看象限.
二、负化正、大化小、化到锐角就“算了”.
三、关注和、关注差、化到已知就“到家”.
师:通过前三节的学习,我们掌握了诱导公式,熟悉如何将一个未知,陌生的问题转化为已知,熟悉的问题的方法,其中蕴含着数学中重要的思想方法:转化与化归的思想。
(2)导入新课,确定研究目标:
今天我们要有请今天的主角隆重登场:和
我们先进行第一次转化:
因此由函数的图象变换法,我们只需研究如何画即可.
除此之外,我们还可以研究正弦函数的哪些性质,以帮助我们减少画图的工作量?
引导学生回答:
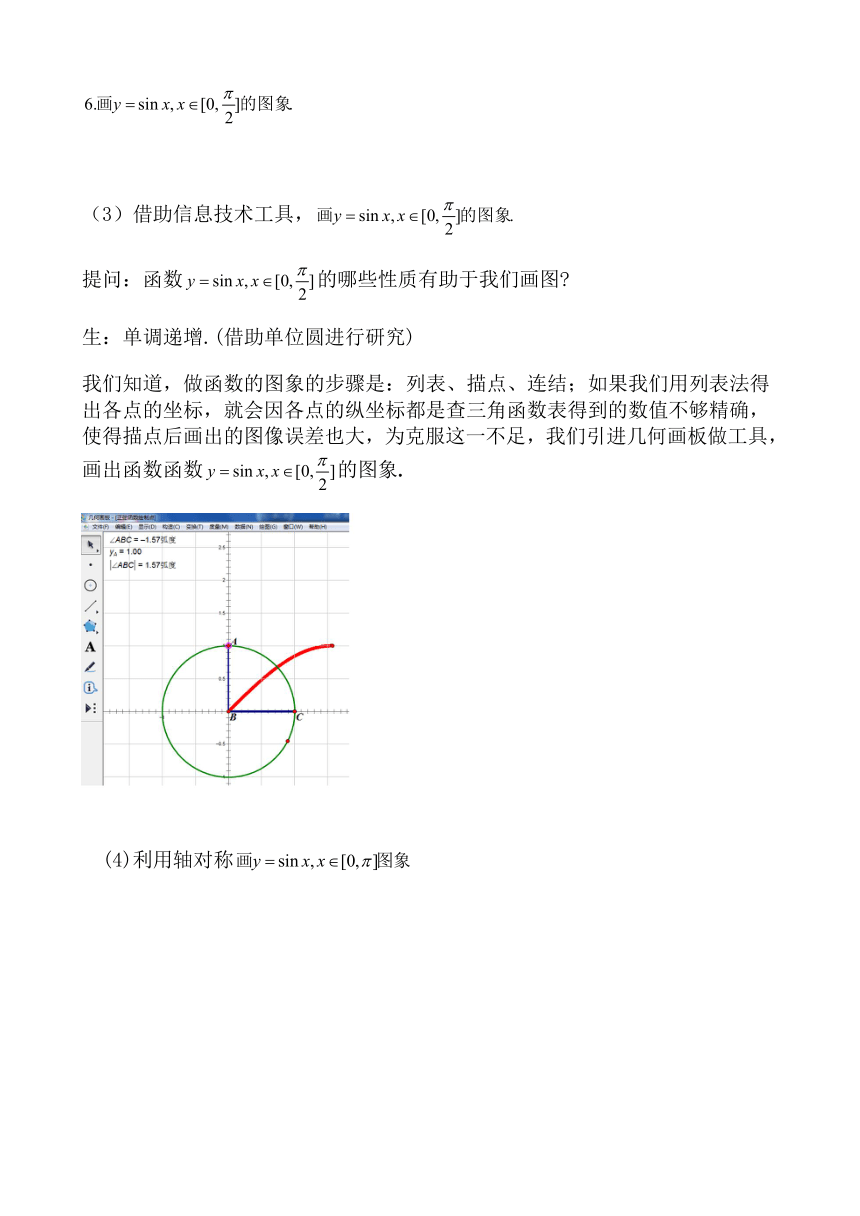
(3)借助信息技术工具,
提问:函数的哪些性质有助于我们画图?
生:单调递增.(借助单位圆进行研究)
我们知道,做函数的图象的步骤是:列表、描点、连结;如果我们用列表法得出各点的坐标,就会因各点的纵坐标都是查三角函数表得到的数值不够精确,使得描点后画出的图像误差也大,为克服这一不足,我们引进几何画板做工具,画出函数函数的图象.
(4)利用轴对称
(5)利用中心对称
(6)利用周期性和中心对称
正弦函数叫做正弦曲线.
(7)五点法作的简图
师:在作正弦函数的图象时,我们描了很多点,但其中起关键作用的是函数
与
轴的交点及最高点和最低点这五个点,你能依次它们的坐标吗?
生:(0,0),
,
,
,
师:事实上,只要指出这五个点,
的图象的形状就基本确定了,以后我们常先找出这五个关键点,然后用光滑的曲线将它们连结起来,就得到函数的简图,这种作图的方法称为“五点法”作图.
(8)用变换法作余弦函数
的图象
因为,所以
与
是同一个函数,即余弦函数的图像可以通过正弦曲线向左平移
个长度单位角得到,余弦函数的图像叫做余弦曲线,如图2,师:请同学们说出在函数
,
的图像上,起关键作用的五个点的坐标.
生:(0,1),
,
,
,
3.例题分析
【例1】画出下列函数的简图:
(1)
,
;
(2)
,
.
解:(1)按五个关键点列表
0
0
1
0
-1
0
1
2
1
0
1
利用五点法作出简图3
师:请说出函数
与
的图像之间有何联系?
生:函数
,
的图像可由
,
的图像向上平移1个单位得到.
(2)按五个关键点列表
0
?
?
?
1
0
-1
0
1
?
-1
0
1
0
-1
利用五点法作出简图4
师:
,
与
,
的图像有何联系?
生:它们的图像关于
轴对称.
4.课后练习
在同一坐标系内,用五点法分别画出函数
和的简图:
5.总结提炼
(1)本课介绍了四种作
,
图像的方法,其中五点作图法最常用,要牢记五个关键点的选取特点.
(2)体会转化与化归思想在本节课的体现,并在其他的数学活动中慢慢体会.
(五)评价分析与课后反思
日本著名数学教育家米山国藏指出:“作为知识的数学出校门不到两年可能就忘了,唯有深深铭记在头脑中的是数学的精神,数学的思想、研究的方法和着眼点等,这些随时随地发生作用,使他们终身受益。”
本节课在教学设计上,不只是让学生接受一个正余弦函数概念知识或简单地记住它们的图象,不只是注重数学形式层面的教学,而是更重视数学发现层面的教学,即让学生在经历“数学家”解决问题的过程中去理解、去感受一种数学的思想和观念──把未知化已知,把陌生化熟悉的数学思想方法——转化与化归的数学思想方法。?
??????
PAGE
教
A
版
数
学
必
修4
P30—34
1.4.1?
正弦函数、余弦函数的图象
(一)教学具准备
直尺、圆规、投影仪.
(二)教学目标
1.了解作正、余弦函数图象的转化过程.
2.掌握五点作图法,并会用此方法作出
上的正弦曲线、余弦曲线.
3.体会转化与化归思想在本节课的应用.
(三)教学设计的基本构想
通过诱导公式对正弦函数基本性质进行研究,利用转化与化归的数学思想方法,将问题由大变小,逐步降低研究问题的难度,达到本节课给出正余弦函数的目的.具体流程如下:
(四)教学过程
1.设置情境
引进弧度制以后,
就可以看做是定义域为R
的实变量函数.作为函数,我们首先要关注其图像特征.本节课我们一起来学习作正、余弦函数图像的方法.
2.探索研究
(1)复习诱导公式
前面我们已经学习过三角函数的诱导公式,即将
的三角函数化为角的某种三角函数值的方法,请同学们回顾:
一、奇变偶不变、符号看象限.
二、负化正、大化小、化到锐角就“算了”.
三、关注和、关注差、化到已知就“到家”.
师:通过前三节的学习,我们掌握了诱导公式,熟悉如何将一个未知,陌生的问题转化为已知,熟悉的问题的方法,其中蕴含着数学中重要的思想方法:转化与化归的思想。
(2)导入新课,确定研究目标:
今天我们要有请今天的主角隆重登场:和
我们先进行第一次转化:
因此由函数的图象变换法,我们只需研究如何画即可.
除此之外,我们还可以研究正弦函数的哪些性质,以帮助我们减少画图的工作量?
引导学生回答:
(3)借助信息技术工具,
提问:函数的哪些性质有助于我们画图?
生:单调递增.(借助单位圆进行研究)
我们知道,做函数的图象的步骤是:列表、描点、连结;如果我们用列表法得出各点的坐标,就会因各点的纵坐标都是查三角函数表得到的数值不够精确,使得描点后画出的图像误差也大,为克服这一不足,我们引进几何画板做工具,画出函数函数的图象.
(4)利用轴对称
(5)利用中心对称
(6)利用周期性和中心对称
正弦函数叫做正弦曲线.
(7)五点法作的简图
师:在作正弦函数的图象时,我们描了很多点,但其中起关键作用的是函数
与
轴的交点及最高点和最低点这五个点,你能依次它们的坐标吗?
生:(0,0),
,
,
,
师:事实上,只要指出这五个点,
的图象的形状就基本确定了,以后我们常先找出这五个关键点,然后用光滑的曲线将它们连结起来,就得到函数的简图,这种作图的方法称为“五点法”作图.
(8)用变换法作余弦函数
的图象
因为,所以
与
是同一个函数,即余弦函数的图像可以通过正弦曲线向左平移
个长度单位角得到,余弦函数的图像叫做余弦曲线,如图2,师:请同学们说出在函数
,
的图像上,起关键作用的五个点的坐标.
生:(0,1),
,
,
,
3.例题分析
【例1】画出下列函数的简图:
(1)
,
;
(2)
,
.
解:(1)按五个关键点列表
0
0
1
0
-1
0
1
2
1
0
1
利用五点法作出简图3
师:请说出函数
与
的图像之间有何联系?
生:函数
,
的图像可由
,
的图像向上平移1个单位得到.
(2)按五个关键点列表
0
?
?
?
1
0
-1
0
1
?
-1
0
1
0
-1
利用五点法作出简图4
师:
,
与
,
的图像有何联系?
生:它们的图像关于
轴对称.
4.课后练习
在同一坐标系内,用五点法分别画出函数
和的简图:
5.总结提炼
(1)本课介绍了四种作
,
图像的方法,其中五点作图法最常用,要牢记五个关键点的选取特点.
(2)体会转化与化归思想在本节课的体现,并在其他的数学活动中慢慢体会.
(五)评价分析与课后反思
日本著名数学教育家米山国藏指出:“作为知识的数学出校门不到两年可能就忘了,唯有深深铭记在头脑中的是数学的精神,数学的思想、研究的方法和着眼点等,这些随时随地发生作用,使他们终身受益。”
本节课在教学设计上,不只是让学生接受一个正余弦函数概念知识或简单地记住它们的图象,不只是注重数学形式层面的教学,而是更重视数学发现层面的教学,即让学生在经历“数学家”解决问题的过程中去理解、去感受一种数学的思想和观念──把未知化已知,把陌生化熟悉的数学思想方法——转化与化归的数学思想方法。?
??????
PAGE
