7.3.2离散型随机变量的方差练习题2020-2021学年高二数学人教A版(2019)选择性必修第三册第七章随机变量及其分布Word含答案解析
文档属性
| 名称 | 7.3.2离散型随机变量的方差练习题2020-2021学年高二数学人教A版(2019)选择性必修第三册第七章随机变量及其分布Word含答案解析 |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 16:06:10 | ||
图片预览




文档简介
离散型随机变量的方差
1.(多选题)已知随机变量X的分布列为
X -1 0 1
P
a
则下列式子正确的是( )
A.P(X=0)= B.a=
C.E(X)=- D.D(X)=
2.设随机变量X的分布列为
X -1 0 1
P
若Y=2X+2,则D(Y)等于( )
A.- B. C. D.
3.抛掷一枚硬币,规定正面向上得1分,反面向上得-1分,则得分X的均值与方差分别为( )
A.E(X)=0,D(X)=1 B.E(X)=,D(X)=
C.E(X)=0,D(X)= D.E(X)=,D(X)=1
4.(多选题)编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的人数是ξ,则( )
A.ξ的所有取值是1,2,3 B.P(ξ=1)=
C.E(ξ)=1 D.D(ξ)=1
5.若某事件在一次试验中发生次数的方差等于0.25,则该事件在一次试验中发生的概率为________.?
6.有10张卡片,其中8张标有数字2,2张标有数字5,若从中随机抽出3张,设这3张卡片上的数字和为X,则D(X)=________.?
7.根据以往经验,一辆从北京开往天津的长途汽车在无雨天盈利230元,小雨天盈利163元,中雨天盈利90元.根据天气预报,明天无雨的概率是0.2,有小雨的概率是0.3,有中雨的概率是0.5.问:明天发一辆长途汽车盈利的期望是多少元?方差和标准差各是多少?
8.设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,若以X和Y分别表示取出次品和正品的个数.
(1)求X的分布列、均值及方差;
(2)求Y的分布列、均值及方差.
扩展练习
1.某同学上学路上要经过3个路口,在每个路口遇到红灯的概率都是,且在各路口是否遇到红灯是相互独立的,记X为遇到红灯的次数,若Y=3X+5,则Y的标准差为( )
A. B.3 C. D.2
2.若X是离散型随机变量,P(X=x1)=,P(X=x2)=,且x1A. B. C.3 D.
3.已知离散型随机变量X的可能取值为x1=-1,x2=0,x3=1,且E(X)=0.1,
D(X)=0.89,则对应x1,x2,x3的概率p1,p2,p3分别为________,_______,_______.
4.一个口袋中装有大小相同的2个白球和4个黑球.若采取放回抽样方式,从中摸出两个球,则两球恰好颜色不同的概率为________,若采取不放回抽样方式,从中摸出两个球,则摸出白球的个数的方差为________.?
5.已知随机变量X的分布列为:
X 0 1 x
P
p
若E(X)=.
(1)求D(X)的值;
(2)若Y=3X-2,求的值.
6.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数大于6环,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的均值与方差,并以此比较甲、乙的射击技术.
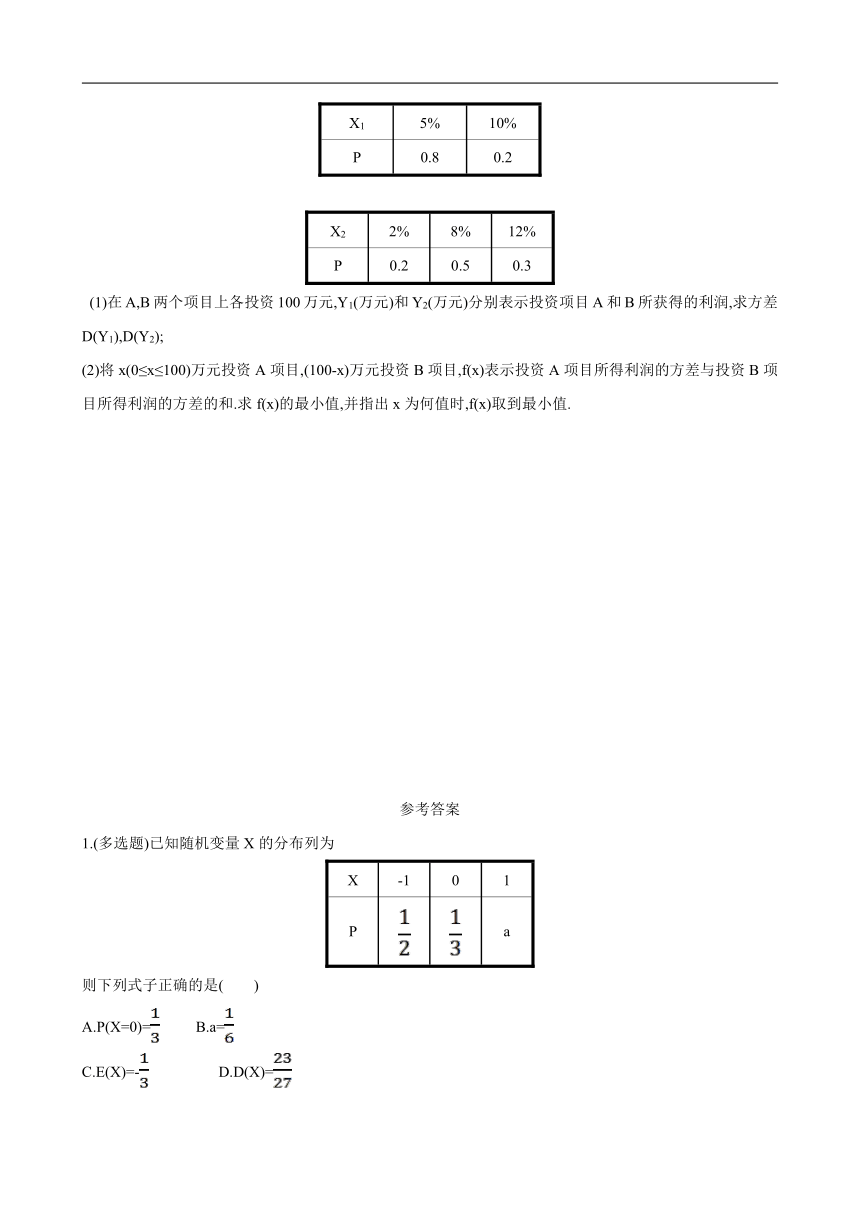
7.A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为
X1 5% 10%
P 0.8 0.2
X2 2% 8% 12%
P 0.2 0.5 0.3
(1)在A,B两个项目上各投资100万元,Y1(万元)和Y2(万元)分别表示投资项目A和B所获得的利润,求方差D(Y1),D(Y2);
(2)将x(0≤x≤100)万元投资A项目,(100-x)万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
参考答案
1.(多选题)已知随机变量X的分布列为
X -1 0 1
P
a
则下列式子正确的是( )
A.P(X=0)= B.a=
C.E(X)=- D.D(X)=
分析:选ABC.由分布列可知,P(X=0)=,a=1--=,
E(X)=(-1)×+0×+1×=-;
D(X)=×+×+×=.
2.设随机变量X的分布列为
X -1 0 1
P
若Y=2X+2,则D(Y)等于( )
A.- B. C. D.
分析:选D.由题意知,E(X)=-1×+0×+1×=-,故D(X)=×+×+×=,
D(Y)=D(2X+2)=4D(X)=4×=.
3.抛掷一枚硬币,规定正面向上得1分,反面向上得-1分,则得分X的均值与方差分别为( )
A.E(X)=0,D(X)=1 B.E(X)=,D(X)=
C.E(X)=0,D(X)= D.E(X)=,D(X)=1
分析:选A.抛掷一枚硬币,规定正面向上得1分,反面向上得-1分,则得分X的分布列为
X 1 -1
P 0.5 0.5
所以E(X)=1×0.5+(-1)×0.5=0,
D(X)=(1-0)2×0.5+(-1-0)2×0.5=1.
4.(多选题)编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的人数是ξ,则( )
A.ξ的所有取值是1,2,3 B.P(ξ=1)=
C.E(ξ)=1 D.D(ξ)=1
分析:选BCD.ξ的所有可能取值为0,1,3,ξ=0表示三位同学全坐错了,有2种情况,即编号为1,2,3的座位上分别坐了编号为2,3,1或3,1,2的学生,
则P(ξ=0)==;ξ=1表示三位同学只有1位同学坐对了,则P(ξ=1)==;
ξ=3表示三位同学全坐对了,即对号入座,
则P(ξ=3)==.所以ξ的分布列为
ξ 0 1 3
P
E(ξ)=0×+1×+3×=1.
D(ξ)=×(0-1)2+×(1-1)2+×(3-1)2=1.
5.若某事件在一次试验中发生次数的方差等于0.25,则该事件在一次试验中发生的概率为________.?
分析:事件在一次试验中发生次数记为X,则X服从两点分布,则D(X)=p(1-p),所以p(1-p)=0.25,解得p=0.5.
答案:0.5
6.有10张卡片,其中8张标有数字2,2张标有数字5,若从中随机抽出3张,设这3张卡片上的数字和为X,则D(X)=________.?
分析:由题意得,随机变量X的可能取值为6,9,12.
P(X=6)==,P(X=9)==,P(X=12)==,
则E(X)=6×+9×+12×=7.8,
D(X)=×(6-7.8)2+×(9-7.8)2+×(12-7.8)2=3.36.
答案:3.36
7.根据以往经验,一辆从北京开往天津的长途汽车在无雨天盈利230元,小雨天盈利163元,中雨天盈利90元.根据天气预报,明天无雨的概率是0.2,有小雨的概率是0.3,有中雨的概率是0.5.问:明天发一辆长途汽车盈利的期望是多少元?方差和标准差各是多少?
分析:用X表示明天发一辆车的盈利,由题意知
P(X=230)=0.2,P(X=163)=0.3,P(X=90)=0.5,
所以E(X)=230×0.2+163×0.3+90×0.5=139.9(元).
所以明天发一辆长途汽车盈利的期望是139.9元.
方差D(X)=(230-139.9)2×0.2+(163-139.9)2×0.3+(90-139.9)2×0.5
=3 028.69,
标准差=≈55.
所以方差和标准差各是3 028.69,55.
8.设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,若以X和Y分别表示取出次品和正品的个数.
(1)求X的分布列、均值及方差;
(2)求Y的分布列、均值及方差.
分析:(1)X的可能值为0,1,2.若X=0,表示没有取出次品,其概率为P(X=0)==,
同理,有P(X=1)==,P(X=2)==.
所以X的分布列为
X 0 1 2
P
所以E(X)=0×+1×+2×=.
D(X)=×+×+×=.
(2)Y的可能值为1,2,3,显然X+Y=3.
P(Y=1)=P(X=2)=,P(Y=2)=P(X=1)=,
P(Y=3)=P(X=0)=.所以Y的分布列为
Y 1 2 3
P
所以Y=-X+3,所以E(Y)=E(3-X)=3-E(X)=3-=,D(Y)=(-1)2D(X)=.
扩展练习
1.某同学上学路上要经过3个路口,在每个路口遇到红灯的概率都是,且在各路口是否遇到红灯是相互独立的,记X为遇到红灯的次数,若Y=3X+5,则Y的标准差为( )
A. B.3 C. D.2
分析:选A.因为该同学经过每个路口时,是否遇到红灯互不影响,所以可看成3次独立重复试验,
即X~B,则X的方差D(X)=3××=,所以Y的方差D(Y)=32·D(X)=9×=6,所以Y的标准差为=.
2.若X是离散型随机变量,P(X=x1)=,P(X=x2)=,且x1A. B. C.3 D.
分析:选C.
x1,x2满足
解得或
因为x13.已知离散型随机变量X的可能取值为x1=-1,x2=0,x3=1,且E(X)=0.1,
D(X)=0.89,则对应x1,x2,x3的概率p1,p2,p3分别为________,_______,_______.
分析:由题意知,-p1+p3=0.1,1.21p1+0.01p2+0.81p3=0.89.
又p1+p2+p3=1,解得p1=0.4,p2=0.1,p3=0.5.
答案:0.4 0.1 0.5
4.一个口袋中装有大小相同的2个白球和4个黑球.若采取放回抽样方式,从中摸出两个球,则两球恰好颜色不同的概率为________,若采取不放回抽样方式,从中摸出两个球,则摸出白球的个数的方差为________.?
分析:“有放回摸取”可看作独立重复试验,
每次摸出一球是白球的概率为p==.
所以“有放回摸两次,颜色不同”的概率为××=.“不放回抽取”时,设摸出白球的个数为X,依题意得P(X=0)==,
P(X=1)==,P(X=2)==.
所以E(X)=0×+1×+2×=,
D(X)=×+×+×=.
答案:
5.已知随机变量X的分布列为:
X 0 1 x
P
p
若E(X)=.
(1)求D(X)的值;
(2)若Y=3X-2,求的值.
分析:由分布列的性质,得++p=1,解得p=,
因为E(X)=0×+1×+x=,所以x=2.
(1)D(X)=×+×+×==.
(2)因为Y=3X-2,所以D(Y)=D(3X-2)=9D(X)=5,所以=.
6.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数大于6环,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的均值与方差,并以此比较甲、乙的射击技术.
分析:(1)由题意得:0.5+3a+a+0.1=1,解得a=0.1.因为乙射中10,9,8环的概率分别为0.3,0.3,0.2.
所以乙射中7环的概率为1-(0.3+0.3+0.2)=0.2.
所以ξ,η的分布列分别为
ξ 10 9 8 7
P 0.5 0.3 0.1 0.1
η 10 9 8 7
P 0.3 0.3 0.2 0.2
(2)由(1)得E(ξ)=10×0.5+9×0.3+8×0.1+7×0.1=9.2;E(η)=10×0.3+9×0.3+8×0.2+7×0.2=8.7;
D(ξ)=(10-9.2)2×0.5+(9-9.2)2×0.3+(8-9.2)2×0.1+(7-9.2)2×0.1=0.96;
D(η)=(10-8.7)2×0.3+(9-8.7)2×0.3+(8-8.7)2×0.2+(7-8.7)2×0.2=1.21.由于E(ξ)>E(η),D(ξ)7.A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为
X1 5% 10%
P 0.8 0.2
X2 2% 8% 12%
P 0.2 0.5 0.3
(1)在A,B两个项目上各投资100万元,Y1(万元)和Y2(万元)分别表示投资项目A和B所获得的利润,求方差D(Y1),D(Y2);
(2)将x(0≤x≤100)万元投资A项目,(100-x)万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
分析:(1)由题设可知Y1和Y2的分布列分别为
Y1 5 10
P 0.8 0.2
Y2 2 8 12
P 0.2 0.5 0.3
E(Y1)=5×0.8+10×0.2=6,
D(Y1)=(5-6)2×0.8+(10-6)2×0.2=4;
E(Y2)=2×0.2+8×0.5+12×0.3=8,
D(Y2)=(2-8)2×0.2+(8-8)2×0.5+(12-8)2×0.3=12.
(2)f(x)=D+D
=D(Y1)+D(Y2)=[x2+3(100-x)2]=(4x2-600x+3×1002).
所以当x==75时,f(x)取最小值3.
1.(多选题)已知随机变量X的分布列为
X -1 0 1
P
a
则下列式子正确的是( )
A.P(X=0)= B.a=
C.E(X)=- D.D(X)=
2.设随机变量X的分布列为
X -1 0 1
P
若Y=2X+2,则D(Y)等于( )
A.- B. C. D.
3.抛掷一枚硬币,规定正面向上得1分,反面向上得-1分,则得分X的均值与方差分别为( )
A.E(X)=0,D(X)=1 B.E(X)=,D(X)=
C.E(X)=0,D(X)= D.E(X)=,D(X)=1
4.(多选题)编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的人数是ξ,则( )
A.ξ的所有取值是1,2,3 B.P(ξ=1)=
C.E(ξ)=1 D.D(ξ)=1
5.若某事件在一次试验中发生次数的方差等于0.25,则该事件在一次试验中发生的概率为________.?
6.有10张卡片,其中8张标有数字2,2张标有数字5,若从中随机抽出3张,设这3张卡片上的数字和为X,则D(X)=________.?
7.根据以往经验,一辆从北京开往天津的长途汽车在无雨天盈利230元,小雨天盈利163元,中雨天盈利90元.根据天气预报,明天无雨的概率是0.2,有小雨的概率是0.3,有中雨的概率是0.5.问:明天发一辆长途汽车盈利的期望是多少元?方差和标准差各是多少?
8.设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,若以X和Y分别表示取出次品和正品的个数.
(1)求X的分布列、均值及方差;
(2)求Y的分布列、均值及方差.
扩展练习
1.某同学上学路上要经过3个路口,在每个路口遇到红灯的概率都是,且在各路口是否遇到红灯是相互独立的,记X为遇到红灯的次数,若Y=3X+5,则Y的标准差为( )
A. B.3 C. D.2
2.若X是离散型随机变量,P(X=x1)=,P(X=x2)=,且x1
3.已知离散型随机变量X的可能取值为x1=-1,x2=0,x3=1,且E(X)=0.1,
D(X)=0.89,则对应x1,x2,x3的概率p1,p2,p3分别为________,_______,_______.
4.一个口袋中装有大小相同的2个白球和4个黑球.若采取放回抽样方式,从中摸出两个球,则两球恰好颜色不同的概率为________,若采取不放回抽样方式,从中摸出两个球,则摸出白球的个数的方差为________.?
5.已知随机变量X的分布列为:
X 0 1 x
P
p
若E(X)=.
(1)求D(X)的值;
(2)若Y=3X-2,求的值.
6.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数大于6环,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的均值与方差,并以此比较甲、乙的射击技术.
7.A,B两个投资项目的利润率分别为随机变量X1和X2.根据市场分析,X1和X2的分布列分别为
X1 5% 10%
P 0.8 0.2
X2 2% 8% 12%
P 0.2 0.5 0.3
(1)在A,B两个项目上各投资100万元,Y1(万元)和Y2(万元)分别表示投资项目A和B所获得的利润,求方差D(Y1),D(Y2);
(2)将x(0≤x≤100)万元投资A项目,(100-x)万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
参考答案
1.(多选题)已知随机变量X的分布列为
X -1 0 1
P
a
则下列式子正确的是( )
A.P(X=0)= B.a=
C.E(X)=- D.D(X)=
分析:选ABC.由分布列可知,P(X=0)=,a=1--=,
E(X)=(-1)×+0×+1×=-;
D(X)=×+×+×=.
2.设随机变量X的分布列为
X -1 0 1
P
若Y=2X+2,则D(Y)等于( )
A.- B. C. D.
分析:选D.由题意知,E(X)=-1×+0×+1×=-,故D(X)=×+×+×=,
D(Y)=D(2X+2)=4D(X)=4×=.
3.抛掷一枚硬币,规定正面向上得1分,反面向上得-1分,则得分X的均值与方差分别为( )
A.E(X)=0,D(X)=1 B.E(X)=,D(X)=
C.E(X)=0,D(X)= D.E(X)=,D(X)=1
分析:选A.抛掷一枚硬币,规定正面向上得1分,反面向上得-1分,则得分X的分布列为
X 1 -1
P 0.5 0.5
所以E(X)=1×0.5+(-1)×0.5=0,
D(X)=(1-0)2×0.5+(-1-0)2×0.5=1.
4.(多选题)编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的人数是ξ,则( )
A.ξ的所有取值是1,2,3 B.P(ξ=1)=
C.E(ξ)=1 D.D(ξ)=1
分析:选BCD.ξ的所有可能取值为0,1,3,ξ=0表示三位同学全坐错了,有2种情况,即编号为1,2,3的座位上分别坐了编号为2,3,1或3,1,2的学生,
则P(ξ=0)==;ξ=1表示三位同学只有1位同学坐对了,则P(ξ=1)==;
ξ=3表示三位同学全坐对了,即对号入座,
则P(ξ=3)==.所以ξ的分布列为
ξ 0 1 3
P
E(ξ)=0×+1×+3×=1.
D(ξ)=×(0-1)2+×(1-1)2+×(3-1)2=1.
5.若某事件在一次试验中发生次数的方差等于0.25,则该事件在一次试验中发生的概率为________.?
分析:事件在一次试验中发生次数记为X,则X服从两点分布,则D(X)=p(1-p),所以p(1-p)=0.25,解得p=0.5.
答案:0.5
6.有10张卡片,其中8张标有数字2,2张标有数字5,若从中随机抽出3张,设这3张卡片上的数字和为X,则D(X)=________.?
分析:由题意得,随机变量X的可能取值为6,9,12.
P(X=6)==,P(X=9)==,P(X=12)==,
则E(X)=6×+9×+12×=7.8,
D(X)=×(6-7.8)2+×(9-7.8)2+×(12-7.8)2=3.36.
答案:3.36
7.根据以往经验,一辆从北京开往天津的长途汽车在无雨天盈利230元,小雨天盈利163元,中雨天盈利90元.根据天气预报,明天无雨的概率是0.2,有小雨的概率是0.3,有中雨的概率是0.5.问:明天发一辆长途汽车盈利的期望是多少元?方差和标准差各是多少?
分析:用X表示明天发一辆车的盈利,由题意知
P(X=230)=0.2,P(X=163)=0.3,P(X=90)=0.5,
所以E(X)=230×0.2+163×0.3+90×0.5=139.9(元).
所以明天发一辆长途汽车盈利的期望是139.9元.
方差D(X)=(230-139.9)2×0.2+(163-139.9)2×0.3+(90-139.9)2×0.5
=3 028.69,
标准差=≈55.
所以方差和标准差各是3 028.69,55.
8.设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,若以X和Y分别表示取出次品和正品的个数.
(1)求X的分布列、均值及方差;
(2)求Y的分布列、均值及方差.
分析:(1)X的可能值为0,1,2.若X=0,表示没有取出次品,其概率为P(X=0)==,
同理,有P(X=1)==,P(X=2)==.
所以X的分布列为
X 0 1 2
P
所以E(X)=0×+1×+2×=.
D(X)=×+×+×=.
(2)Y的可能值为1,2,3,显然X+Y=3.
P(Y=1)=P(X=2)=,P(Y=2)=P(X=1)=,
P(Y=3)=P(X=0)=.所以Y的分布列为
Y 1 2 3
P
所以Y=-X+3,所以E(Y)=E(3-X)=3-E(X)=3-=,D(Y)=(-1)2D(X)=.
扩展练习
1.某同学上学路上要经过3个路口,在每个路口遇到红灯的概率都是,且在各路口是否遇到红灯是相互独立的,记X为遇到红灯的次数,若Y=3X+5,则Y的标准差为( )
A. B.3 C. D.2
分析:选A.因为该同学经过每个路口时,是否遇到红灯互不影响,所以可看成3次独立重复试验,
即X~B,则X的方差D(X)=3××=,所以Y的方差D(Y)=32·D(X)=9×=6,所以Y的标准差为=.
2.若X是离散型随机变量,P(X=x1)=,P(X=x2)=,且x1
分析:选C.
x1,x2满足
解得或
因为x1
D(X)=0.89,则对应x1,x2,x3的概率p1,p2,p3分别为________,_______,_______.
分析:由题意知,-p1+p3=0.1,1.21p1+0.01p2+0.81p3=0.89.
又p1+p2+p3=1,解得p1=0.4,p2=0.1,p3=0.5.
答案:0.4 0.1 0.5
4.一个口袋中装有大小相同的2个白球和4个黑球.若采取放回抽样方式,从中摸出两个球,则两球恰好颜色不同的概率为________,若采取不放回抽样方式,从中摸出两个球,则摸出白球的个数的方差为________.?
分析:“有放回摸取”可看作独立重复试验,
每次摸出一球是白球的概率为p==.
所以“有放回摸两次,颜色不同”的概率为××=.“不放回抽取”时,设摸出白球的个数为X,依题意得P(X=0)==,
P(X=1)==,P(X=2)==.
所以E(X)=0×+1×+2×=,
D(X)=×+×+×=.
答案:
5.已知随机变量X的分布列为:
X 0 1 x
P
p
若E(X)=.
(1)求D(X)的值;
(2)若Y=3X-2,求的值.
分析:由分布列的性质,得++p=1,解得p=,
因为E(X)=0×+1×+x=,所以x=2.
(1)D(X)=×+×+×==.
(2)因为Y=3X-2,所以D(Y)=D(3X-2)=9D(X)=5,所以=.
6.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数大于6环,且甲射中10,9,8,7环的概率分别为0.5,3a,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.
(1)求ξ,η的分布列;
(2)求ξ,η的均值与方差,并以此比较甲、乙的射击技术.
分析:(1)由题意得:0.5+3a+a+0.1=1,解得a=0.1.因为乙射中10,9,8环的概率分别为0.3,0.3,0.2.
所以乙射中7环的概率为1-(0.3+0.3+0.2)=0.2.
所以ξ,η的分布列分别为
ξ 10 9 8 7
P 0.5 0.3 0.1 0.1
η 10 9 8 7
P 0.3 0.3 0.2 0.2
(2)由(1)得E(ξ)=10×0.5+9×0.3+8×0.1+7×0.1=9.2;E(η)=10×0.3+9×0.3+8×0.2+7×0.2=8.7;
D(ξ)=(10-9.2)2×0.5+(9-9.2)2×0.3+(8-9.2)2×0.1+(7-9.2)2×0.1=0.96;
D(η)=(10-8.7)2×0.3+(9-8.7)2×0.3+(8-8.7)2×0.2+(7-8.7)2×0.2=1.21.由于E(ξ)>E(η),D(ξ)
X1 5% 10%
P 0.8 0.2
X2 2% 8% 12%
P 0.2 0.5 0.3
(1)在A,B两个项目上各投资100万元,Y1(万元)和Y2(万元)分别表示投资项目A和B所获得的利润,求方差D(Y1),D(Y2);
(2)将x(0≤x≤100)万元投资A项目,(100-x)万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
分析:(1)由题设可知Y1和Y2的分布列分别为
Y1 5 10
P 0.8 0.2
Y2 2 8 12
P 0.2 0.5 0.3
E(Y1)=5×0.8+10×0.2=6,
D(Y1)=(5-6)2×0.8+(10-6)2×0.2=4;
E(Y2)=2×0.2+8×0.5+12×0.3=8,
D(Y2)=(2-8)2×0.2+(8-8)2×0.5+(12-8)2×0.3=12.
(2)f(x)=D+D
=D(Y1)+D(Y2)=[x2+3(100-x)2]=(4x2-600x+3×1002).
所以当x==75时,f(x)取最小值3.
