8.1成对数据的统计相关性练习题2020-2021学年高二数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析
文档属性
| 名称 | 8.1成对数据的统计相关性练习题2020-2021学年高二数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览





文档简介
成对数据的统计相关性
1.(多选题)以下各对变量成正相关的是( )
A.学生的学籍号与学生的数学成绩
B.坚持每天吃早餐的人数与患胃病的人数
C.气温与冷饮销售量
D.电瓶车的重量和行驶每千米的耗电量
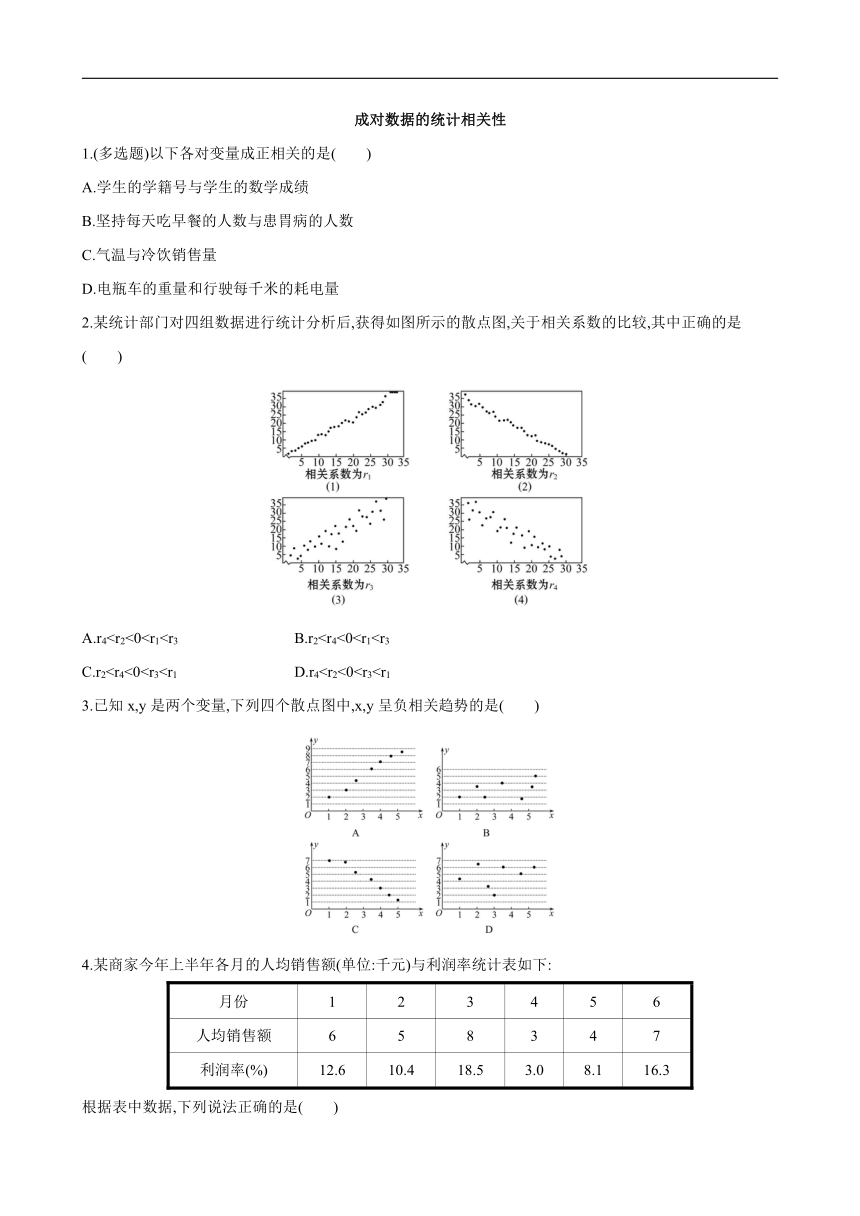
2.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A.r4C.r23.已知x,y是两个变量,下列四个散点图中,x,y呈负相关趋势的是( )
4.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
5.对于线性相关系数r,叙述正确的是( )
A.|r|∈(0,+∞),|r|越大相关程度越大,反之相关程度越小
B.r∈(-∞,+∞),r越大相关程度越大,反之相关程度越小
C.|r|≤1,且|r|越接近1相关程度越大,|r|越接近0,相关程度越小
D.以上说法都不对
6.下列两个变量之间具有相关关系的是________.(填序号)?
①正方形的边长a和面积S;
②一个人的身高h和右手一拃长x;
③真空中的自由落体运动其下落的距离h和下落的时间t;
④一个人的身高h和体重x.
7.下列说法中正确的是________(填序号).?
①变量间的线性相关系数r的取值范围为[-1,1];
②变量间的线性相关系数r的绝对值越接近0,则变量间的线性相关程度越低;
③变量间的相关系数越小,变量间的相关程度越小.
8.某厂的生产原料耗费x(单位:百万元)与销售额Y(单位:百万元)之间有如下的对应关系:
x 2 4 6 8
Y 30 40 50 70
x与Y之间是否具有线性相关关系?若有,判断相关性的强弱.
9.为分析肥胖程度对总胆固醇与空腹血糖的影响,在肥胖人群中随机抽出8人,他们的肥胖指数BMI值、总胆固醇TC指标值(单位:mmol/L)、空腹血糖CLU指标值(单位:mmol/L)如表所示.
人员 编号 1 2 3 4 5 6 7 8
BMI 值x 25 27 30 32 33 35 40 42
TC指标 值y 5.3 5.4 5.5 5.6 5.7 6.5 6.9 7.1
CLU指 标值z 6.7 7.2 7.3 8.0 8.1 8.6 9.0 9.1
用变量y与x,z与x的相关系数,分别说明TC指标值与BMI值、CLU指标值与BMI值的相关程度;
参考公式:
相关系数r=
参考数据:=33,=6,=8,(xi-)2=244,(yi-)2≈3.6,(zi-)2=5.4,(xi-)(yi-)=28.3,
(xi-)(zi-)=35.4,≈15.6,≈1.9,≈2.3.
扩展练习
1.对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断正确的是
( )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C.变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D.变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
2.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,则这组样本数据的样本相关系数为( )
A.-1 B.1 C.- D.
3.在一组数据为(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若这组样本数据的相关系数为-1,则所有的样本点(xi,yi)(i=1,2,…,n)满足的方程可以是( )
A.y=-x-1 B.y=x-1
C.y=x+1 D.y=-x2
4.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数.r2表示变量V与U之间的线性相关系数,则r1,r2,0的大小关系为________.?
5.炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料熔化完毕时钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一组数据,如表所示:
x(0.01%) 104 180 190 177 147 134 150 191 204 121
y(min) 100 200 210 185 155 135 170 205 235 125
判断含碳量与冶炼时间的相关关系的强弱.
6.商务部会同海关总署、国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取 次数 1 2 3 4 5 6 7 8
医疗物 资尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取 次数 9 10 11 12 13 14 15 16
医疗物 资尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=xi=9.97,s==≈0.212,≈18.439,≈1 591.137,(xi-)(i-8.5)=-2.78,其中xi为抽取的第i个医疗物资的尺寸,i=1,2,3,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在(-3s,+3s)之外的医疗物资,就认为这条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查?
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=
.
参考答案
1.(多选题)以下各对变量成正相关的是( )
A.学生的学籍号与学生的数学成绩
B.坚持每天吃早餐的人数与患胃病的人数
C.气温与冷饮销售量
D.电瓶车的重量和行驶每千米的耗电量
分析:选CD.对于A,学生的学籍号与学生的数学成绩没有相关关系;对于B,一般情况下,坚持每天吃早餐的人数与患胃病的人数成负相关关系;对于C,一般情况下,气温与冷饮销售量成正相关关系;对于D,一般情况下,电瓶车的重量和行驶每千米的耗电量成正相关关系.
2.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A.r4C.r2分析:选C.根据散点图的特征,数据大致呈增长趋势的是正相关,数据呈递减趋势的是负相关;数据越集中在一条线附近,说明相关性越强,由题中数据可知:(1)(3)为正相关,(2)(4)为负相关;
故r1>0,r3>0;r2<0,r4<0;又(1)与(2)中散点图更接近于一条直线,故r1>r3,r23.已知x,y是两个变量,下列四个散点图中,x,y呈负相关趋势的是( )
分析:选C.对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关关系;对于B,散点图中的点没有明显的相关关系;对于C,散点图中的点从左向右是下降的,且在一条直线附近,是负相关关系;对于D,散点图中的点没有明显的相关关系.
4.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
分析:选C.根据题意,画出利润率与人均销售额的散点图,如图所示:
由散点图知,利润率与人均销售额成正相关关系.
5.对于线性相关系数r,叙述正确的是( )
A.|r|∈(0,+∞),|r|越大相关程度越大,反之相关程度越小
B.r∈(-∞,+∞),r越大相关程度越大,反之相关程度越小
C.|r|≤1,且|r|越接近1相关程度越大,|r|越接近0,相关程度越小
D.以上说法都不对
分析:选C.用相关系数r可以衡量两个变量之间的相关关系的强弱,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值接近于0时,表示两个变量之间几乎不存在相关关系.
6.下列两个变量之间具有相关关系的是________.(填序号)?
①正方形的边长a和面积S;
②一个人的身高h和右手一拃长x;
③真空中的自由落体运动其下落的距离h和下落的时间t;
④一个人的身高h和体重x.
分析:对于①,正方形的边长a和面积S是函数关系,不是相关关系;对于②,一般情况下,一个人的身高h和右手一拃长x是正相关关系;对于③,真空中的自由落体运动其下落的距离h和下落的时间t是函数关系,不是相关关系;对于④,一般情况下,一个人的身高h和他的体重x是正相关关系.
答案:②④
7.下列说法中正确的是________(填序号).?
①变量间的线性相关系数r的取值范围为[-1,1];
②变量间的线性相关系数r的绝对值越接近0,则变量间的线性相关程度越低;
③变量间的相关系数越小,变量间的相关程度越小.
分析:根据题意,依次分析.对于①,相关系数r满足|r|≤1,即相关系数r的取值范围为[-1,1],①正确;
对于②,根据相关系数的性质知|r|≤1,且|r|越接近1,相关程度越大;|r|越接近0,相关程度越小,则②正确;
对于③,当r接近-1时,变量间的相关程度比r接近0时的大,故③错误.
答案:①②
8.某厂的生产原料耗费x(单位:百万元)与销售额Y(单位:百万元)之间有如下的对应关系:
x 2 4 6 8
Y 30 40 50 70
x与Y之间是否具有线性相关关系?若有,判断相关性的强弱.
分析:画出散点图如图所示,由图可知x,Y有线性关系.
=5,=47.5,=120,=9 900,xiyi=1 080,r=
=≈0.982 7.
故x与Y之间具有很强的正相关关系.
9.为分析肥胖程度对总胆固醇与空腹血糖的影响,在肥胖人群中随机抽出8人,他们的肥胖指数BMI值、总胆固醇TC指标值(单位:mmol/L)、空腹血糖CLU指标值(单位:mmol/L)如表所示.
人员 编号 1 2 3 4 5 6 7 8
BMI 值x 25 27 30 32 33 35 40 42
TC指标 值y 5.3 5.4 5.5 5.6 5.7 6.5 6.9 7.1
CLU指 标值z 6.7 7.2 7.3 8.0 8.1 8.6 9.0 9.1
用变量y与x,z与x的相关系数,分别说明TC指标值与BMI值、CLU指标值与BMI值的相关程度;
参考公式:
相关系数r=
参考数据:=33,=6,=8,(xi-)2=244,(yi-)2≈3.6,(zi-)2=5.4,(xi-)(yi-)=28.3,
(xi-)(zi-)=35.4,≈15.6,≈1.9,≈2.3.
分析:变量y与x的相关系数r≈≈0.95,
变量z与x的相关系数r′≈≈0.99,可以看出TC指标值与BMI值、CLU指标值与BMI值都是高度正相关.
扩展练习
1.对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断正确的是
( )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C.变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D.变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
分析:选C.由线性相关系数r1=0.785 9>0知x与y正相关,由线性相关系数r2=-0.956 8<0知u,v负相关,又|r1|<|r2|,所以变量u与v的线性相关性比x与y的线性相关性强.
2.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,则这组样本数据的样本相关系数为( )
A.-1 B.1 C.- D.
分析:选A.因为这组样本数据的所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,
所以这组样本数据完全相关,其相关系数是-1.
3.在一组数据为(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若这组样本数据的相关系数为-1,则所有的样本点(xi,yi)(i=1,2,…,n)满足的方程可以是( )
A.y=-x-1 B.y=x-1
C.y=x+1 D.y=-x2
分析:选A.若这组样本数据的相关系数为-1,则样本数据为线性相关,排除D,又相关系数为-1,所以样本数据为负相关,排除B,C(B,C为正相关).3.(5分)如图所示的五组数据(x,y)中,去掉________后,剩下的四组数据相关性增强.?
分析:去掉点(4,10)后,其余四点大致在一条直线附近,相关性增强.
答案:(4,10)
4.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数.r2表示变量V与U之间的线性相关系数,则r1,r2,0的大小关系为________.?
分析:对于变量X与Y而言,Y随X的增大而增大,故变量Y与X正相关,即r1>0;对于变量U与V而言,V随U的增大而减小,故变量V与U负相关,即r2<0.故r2<0答案:r2<05.炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料熔化完毕时钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一组数据,如表所示:
x(0.01%) 104 180 190 177 147 134 150 191 204 121
y(min) 100 200 210 185 155 135 170 205 235 125
判断含碳量与冶炼时间的相关关系的强弱.
分析:由已知数据列成下表.
i 1 2 3 4 5 6 7 8 9 10
xi 104 180 190 177 147 134 150 191 204 121
yi 100 200 210 185 155 135 170 205 235 125
xiyi 10 400 36 000 39 900 32 745 22 785 18 090 25 500 39 155 47 940 15 125
=159.8,=172, =265 448,=312 350,xiyi=287 640
于是r=≈0.990 6.y与x具有很强的线性相关关系.
6.商务部会同海关总署、国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取 次数 1 2 3 4 5 6 7 8
医疗物 资尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取 次数 9 10 11 12 13 14 15 16
医疗物 资尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=xi=9.97,s==≈0.212,≈18.439,≈1 591.137,(xi-)(i-8.5)=-2.78,其中xi为抽取的第i个医疗物资的尺寸,i=1,2,3,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在(-3s,+3s)之外的医疗物资,就认为这条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查?
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=
.
分析:(1)由样本数据得(x,i)(i=1,2,3,…,16)的相关系数为
r==
≈-0.18;
由于|r|<0.25,因此可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小.
(2)由于=9.97,s≈0.212,
由样本数据可以看出抽取的第13个零件的尺寸在(-3s,+3s)以外,因此需对当天的生产过程进行检查.
1.(多选题)以下各对变量成正相关的是( )
A.学生的学籍号与学生的数学成绩
B.坚持每天吃早餐的人数与患胃病的人数
C.气温与冷饮销售量
D.电瓶车的重量和行驶每千米的耗电量
2.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A.r4
4.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
5.对于线性相关系数r,叙述正确的是( )
A.|r|∈(0,+∞),|r|越大相关程度越大,反之相关程度越小
B.r∈(-∞,+∞),r越大相关程度越大,反之相关程度越小
C.|r|≤1,且|r|越接近1相关程度越大,|r|越接近0,相关程度越小
D.以上说法都不对
6.下列两个变量之间具有相关关系的是________.(填序号)?
①正方形的边长a和面积S;
②一个人的身高h和右手一拃长x;
③真空中的自由落体运动其下落的距离h和下落的时间t;
④一个人的身高h和体重x.
7.下列说法中正确的是________(填序号).?
①变量间的线性相关系数r的取值范围为[-1,1];
②变量间的线性相关系数r的绝对值越接近0,则变量间的线性相关程度越低;
③变量间的相关系数越小,变量间的相关程度越小.
8.某厂的生产原料耗费x(单位:百万元)与销售额Y(单位:百万元)之间有如下的对应关系:
x 2 4 6 8
Y 30 40 50 70
x与Y之间是否具有线性相关关系?若有,判断相关性的强弱.
9.为分析肥胖程度对总胆固醇与空腹血糖的影响,在肥胖人群中随机抽出8人,他们的肥胖指数BMI值、总胆固醇TC指标值(单位:mmol/L)、空腹血糖CLU指标值(单位:mmol/L)如表所示.
人员 编号 1 2 3 4 5 6 7 8
BMI 值x 25 27 30 32 33 35 40 42
TC指标 值y 5.3 5.4 5.5 5.6 5.7 6.5 6.9 7.1
CLU指 标值z 6.7 7.2 7.3 8.0 8.1 8.6 9.0 9.1
用变量y与x,z与x的相关系数,分别说明TC指标值与BMI值、CLU指标值与BMI值的相关程度;
参考公式:
相关系数r=
参考数据:=33,=6,=8,(xi-)2=244,(yi-)2≈3.6,(zi-)2=5.4,(xi-)(yi-)=28.3,
(xi-)(zi-)=35.4,≈15.6,≈1.9,≈2.3.
扩展练习
1.对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断正确的是
( )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C.变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D.变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
2.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,则这组样本数据的样本相关系数为( )
A.-1 B.1 C.- D.
3.在一组数据为(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若这组样本数据的相关系数为-1,则所有的样本点(xi,yi)(i=1,2,…,n)满足的方程可以是( )
A.y=-x-1 B.y=x-1
C.y=x+1 D.y=-x2
4.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数.r2表示变量V与U之间的线性相关系数,则r1,r2,0的大小关系为________.?
5.炼钢是一个氧化降碳的过程,钢水含碳量的多少直接影响冶炼时间的长短,必须掌握钢水含碳量和冶炼时间的关系.如果已测得炉料熔化完毕时钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一组数据,如表所示:
x(0.01%) 104 180 190 177 147 134 150 191 204 121
y(min) 100 200 210 185 155 135 170 205 235 125
判断含碳量与冶炼时间的相关关系的强弱.
6.商务部会同海关总署、国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取 次数 1 2 3 4 5 6 7 8
医疗物 资尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取 次数 9 10 11 12 13 14 15 16
医疗物 资尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=xi=9.97,s==≈0.212,≈18.439,≈1 591.137,(xi-)(i-8.5)=-2.78,其中xi为抽取的第i个医疗物资的尺寸,i=1,2,3,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在(-3s,+3s)之外的医疗物资,就认为这条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查?
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=
.
参考答案
1.(多选题)以下各对变量成正相关的是( )
A.学生的学籍号与学生的数学成绩
B.坚持每天吃早餐的人数与患胃病的人数
C.气温与冷饮销售量
D.电瓶车的重量和行驶每千米的耗电量
分析:选CD.对于A,学生的学籍号与学生的数学成绩没有相关关系;对于B,一般情况下,坚持每天吃早餐的人数与患胃病的人数成负相关关系;对于C,一般情况下,气温与冷饮销售量成正相关关系;对于D,一般情况下,电瓶车的重量和行驶每千米的耗电量成正相关关系.
2.某统计部门对四组数据进行统计分析后,获得如图所示的散点图,关于相关系数的比较,其中正确的是( )
A.r4
故r1>0,r3>0;r2<0,r4<0;又(1)与(2)中散点图更接近于一条直线,故r1>r3,r2
分析:选C.对于A,散点图中的点从左向右是上升的,且在一条直线附近,是正相关关系;对于B,散点图中的点没有明显的相关关系;对于C,散点图中的点从左向右是下降的,且在一条直线附近,是负相关关系;对于D,散点图中的点没有明显的相关关系.
4.某商家今年上半年各月的人均销售额(单位:千元)与利润率统计表如下:
月份 1 2 3 4 5 6
人均销售额 6 5 8 3 4 7
利润率(%) 12.6 10.4 18.5 3.0 8.1 16.3
根据表中数据,下列说法正确的是( )
A.利润率与人均销售额成正比例函数关系
B.利润率与人均销售额成反比例函数关系
C.利润率与人均销售额成正相关关系
D.利润率与人均销售额成负相关关系
分析:选C.根据题意,画出利润率与人均销售额的散点图,如图所示:
由散点图知,利润率与人均销售额成正相关关系.
5.对于线性相关系数r,叙述正确的是( )
A.|r|∈(0,+∞),|r|越大相关程度越大,反之相关程度越小
B.r∈(-∞,+∞),r越大相关程度越大,反之相关程度越小
C.|r|≤1,且|r|越接近1相关程度越大,|r|越接近0,相关程度越小
D.以上说法都不对
分析:选C.用相关系数r可以衡量两个变量之间的相关关系的强弱,r的绝对值越接近于1,表示两个变量的线性相关性越强,r的绝对值接近于0时,表示两个变量之间几乎不存在相关关系.
6.下列两个变量之间具有相关关系的是________.(填序号)?
①正方形的边长a和面积S;
②一个人的身高h和右手一拃长x;
③真空中的自由落体运动其下落的距离h和下落的时间t;
④一个人的身高h和体重x.
分析:对于①,正方形的边长a和面积S是函数关系,不是相关关系;对于②,一般情况下,一个人的身高h和右手一拃长x是正相关关系;对于③,真空中的自由落体运动其下落的距离h和下落的时间t是函数关系,不是相关关系;对于④,一般情况下,一个人的身高h和他的体重x是正相关关系.
答案:②④
7.下列说法中正确的是________(填序号).?
①变量间的线性相关系数r的取值范围为[-1,1];
②变量间的线性相关系数r的绝对值越接近0,则变量间的线性相关程度越低;
③变量间的相关系数越小,变量间的相关程度越小.
分析:根据题意,依次分析.对于①,相关系数r满足|r|≤1,即相关系数r的取值范围为[-1,1],①正确;
对于②,根据相关系数的性质知|r|≤1,且|r|越接近1,相关程度越大;|r|越接近0,相关程度越小,则②正确;
对于③,当r接近-1时,变量间的相关程度比r接近0时的大,故③错误.
答案:①②
8.某厂的生产原料耗费x(单位:百万元)与销售额Y(单位:百万元)之间有如下的对应关系:
x 2 4 6 8
Y 30 40 50 70
x与Y之间是否具有线性相关关系?若有,判断相关性的强弱.
分析:画出散点图如图所示,由图可知x,Y有线性关系.
=5,=47.5,=120,=9 900,xiyi=1 080,r=
=≈0.982 7.
故x与Y之间具有很强的正相关关系.
9.为分析肥胖程度对总胆固醇与空腹血糖的影响,在肥胖人群中随机抽出8人,他们的肥胖指数BMI值、总胆固醇TC指标值(单位:mmol/L)、空腹血糖CLU指标值(单位:mmol/L)如表所示.
人员 编号 1 2 3 4 5 6 7 8
BMI 值x 25 27 30 32 33 35 40 42
TC指标 值y 5.3 5.4 5.5 5.6 5.7 6.5 6.9 7.1
CLU指 标值z 6.7 7.2 7.3 8.0 8.1 8.6 9.0 9.1
用变量y与x,z与x的相关系数,分别说明TC指标值与BMI值、CLU指标值与BMI值的相关程度;
参考公式:
相关系数r=
参考数据:=33,=6,=8,(xi-)2=244,(yi-)2≈3.6,(zi-)2=5.4,(xi-)(yi-)=28.3,
(xi-)(zi-)=35.4,≈15.6,≈1.9,≈2.3.
分析:变量y与x的相关系数r≈≈0.95,
变量z与x的相关系数r′≈≈0.99,可以看出TC指标值与BMI值、CLU指标值与BMI值都是高度正相关.
扩展练习
1.对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断正确的是
( )
A.变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B.变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C.变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D.变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
分析:选C.由线性相关系数r1=0.785 9>0知x与y正相关,由线性相关系数r2=-0.956 8<0知u,v负相关,又|r1|<|r2|,所以变量u与v的线性相关性比x与y的线性相关性强.
2.在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,则这组样本数据的样本相关系数为( )
A.-1 B.1 C.- D.
分析:选A.因为这组样本数据的所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+1上,
所以这组样本数据完全相关,其相关系数是-1.
3.在一组数据为(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不全相等)的散点图中,若这组样本数据的相关系数为-1,则所有的样本点(xi,yi)(i=1,2,…,n)满足的方程可以是( )
A.y=-x-1 B.y=x-1
C.y=x+1 D.y=-x2
分析:选A.若这组样本数据的相关系数为-1,则样本数据为线性相关,排除D,又相关系数为-1,所以样本数据为负相关,排除B,C(B,C为正相关).3.(5分)如图所示的五组数据(x,y)中,去掉________后,剩下的四组数据相关性增强.?
分析:去掉点(4,10)后,其余四点大致在一条直线附近,相关性增强.
答案:(4,10)
4.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数.r2表示变量V与U之间的线性相关系数,则r1,r2,0的大小关系为________.?
分析:对于变量X与Y而言,Y随X的增大而增大,故变量Y与X正相关,即r1>0;对于变量U与V而言,V随U的增大而减小,故变量V与U负相关,即r2<0.故r2<0
x(0.01%) 104 180 190 177 147 134 150 191 204 121
y(min) 100 200 210 185 155 135 170 205 235 125
判断含碳量与冶炼时间的相关关系的强弱.
分析:由已知数据列成下表.
i 1 2 3 4 5 6 7 8 9 10
xi 104 180 190 177 147 134 150 191 204 121
yi 100 200 210 185 155 135 170 205 235 125
xiyi 10 400 36 000 39 900 32 745 22 785 18 090 25 500 39 155 47 940 15 125
=159.8,=172, =265 448,=312 350,xiyi=287 640
于是r=≈0.990 6.y与x具有很强的线性相关关系.
6.商务部会同海关总署、国家药监局于3月31日发布关于有序开展医疗物资出口的公告.如医疗物资出口中出现质量问题,将认真调查,发现一起,查处一起,切实维护“中国制造”的形象,更好地发挥医疗物资对支持全球疫情防控的重要作用.为了监控某种医疗物资的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个医疗物资,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个医疗物资的尺寸:
抽取 次数 1 2 3 4 5 6 7 8
医疗物 资尺寸 9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04
抽取 次数 9 10 11 12 13 14 15 16
医疗物 资尺寸 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95
经计算得=xi=9.97,s==≈0.212,≈18.439,≈1 591.137,(xi-)(i-8.5)=-2.78,其中xi为抽取的第i个医疗物资的尺寸,i=1,2,3,…,16.
(1)求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为医疗物资尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检医疗物资中,如果出现了尺寸在(-3s,+3s)之外的医疗物资,就认为这条生产线在这一天的生产过程中可能出现了异常情况,需对当天的生产过程进行检查.从这一天抽检的结果看,是否需对当天的生产过程进行检查?
附:样本(xi,yi)(i=1,2,…,n)的相关系数r=
.
分析:(1)由样本数据得(x,i)(i=1,2,3,…,16)的相关系数为
r==
≈-0.18;
由于|r|<0.25,因此可以认为这一天生产的医疗物资尺寸不随生产过程的进行而系统地变大或变小.
(2)由于=9.97,s≈0.212,
由样本数据可以看出抽取的第13个零件的尺寸在(-3s,+3s)以外,因此需对当天的生产过程进行检查.
