8.3.1列联表与独立性检验练习题2020-2021学年高二数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析
文档属性
| 名称 | 8.3.1列联表与独立性检验练习题2020-2021学年高二数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析 |
|
|
| 格式 | doc | ||
| 文件大小 | 756.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 16:56:17 | ||
图片预览




文档简介
列联表与独立性检验
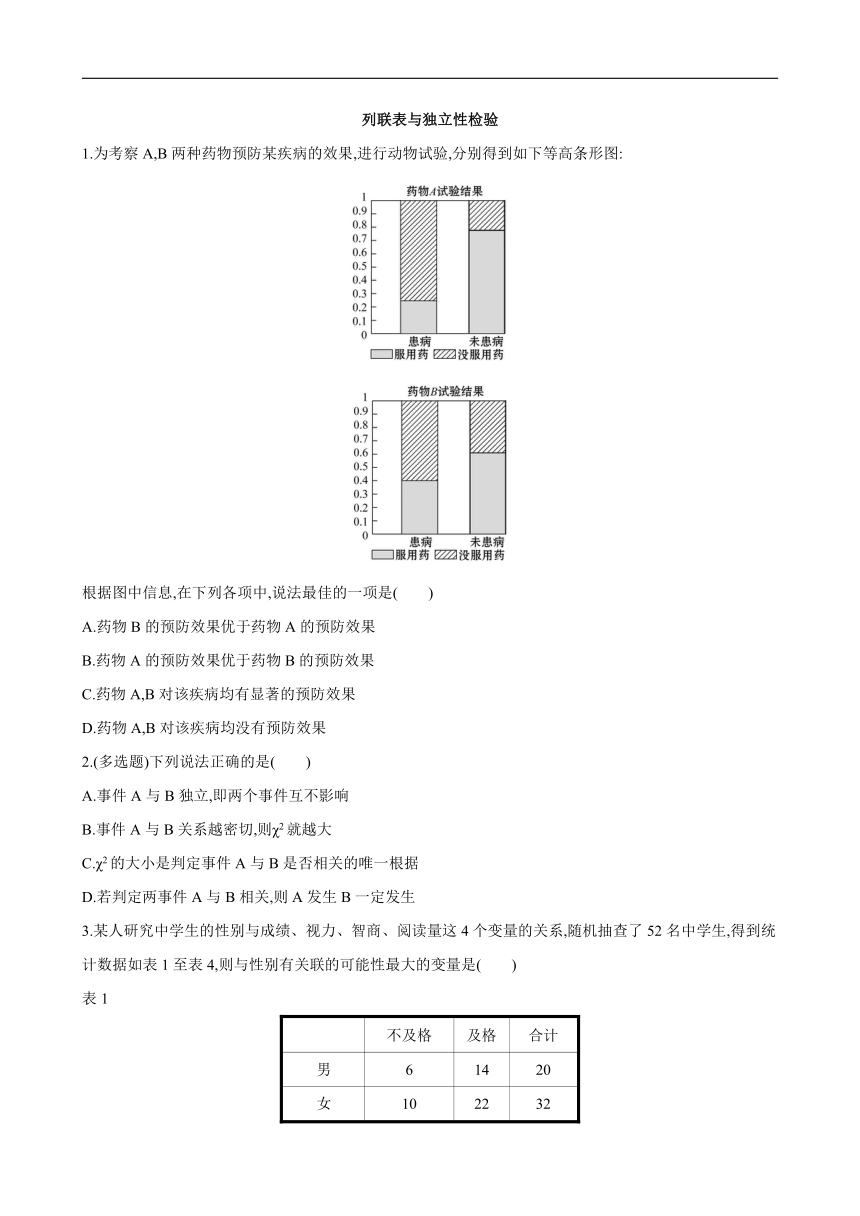
1.为考察A,B两种药物预防某疾病的效果,进行动物试验,分别得到如下等高条形图:
根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物B的预防效果优于药物A的预防效果
B.药物A的预防效果优于药物B的预防效果
C.药物A,B对该疾病均有显著的预防效果
D.药物A,B对该疾病均没有预防效果
2.(多选题)下列说法正确的是( )
A.事件A与B独立,即两个事件互不影响
B.事件A与B关系越密切,则χ2就越大
C.χ2的大小是判定事件A与B是否相关的唯一根据
D.若判定两事件A与B相关,则A发生B一定发生
3.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )
表1
不及格 及格 合计
男 6 14 20
女 10 22 32
合计 16 36 52
表2
好 差 合计
男 4 16 20
女 12 20 32
合计 16 36 52
表3
偏高 正常 合计
男 8 12 20
女 8 24 32
合计 16 36 52
表4
丰富 不丰富 合计
男 14 6 20
女 2 30 32
合计 16 36 52
A.成绩 B.视力 C.智商 D.阅读量
4.有两个分类变量X,Y,其列联表如下所示,
Y1 Y2
X1 a 20-a
X2 15-a 30+a
其中a,15-a均为大于5的整数,若在犯错误的概率不超过0.05的前提下认为X,Y有关,则a的值为( )
A.8 B.9 C.8或9 D.6或8
5.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算χ2=7.63,根据这一数据分析,是否有99.9%的把握说,打鼾与患心脏病是有关的:________.(填“是”或“否”)?
6.如果根据性别与是否爱好运动的列联表得到χ2≈3.852>3.841,则判断性别与是否爱好运动有关,那么这种判断犯错误的可能性不超过________.?
7.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共60人,患胃病者生活规律的共20人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共200人.
(1)根据以上数据列出2×2列联表;
(2)在犯错误的概率不超过0.01的前提下能否认为40岁以上的人患胃病与否和生活规律有关系?为什么?
8.“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1)写出2×2列联表;
(2)能否在犯错误的概率不超过0.1的前提下认为猜对歌曲名称与年龄有关系?说明你的理由.(下面的临界值表供参考)
α 0.1 0.05 0.01 0.005
xα 2.706 3.841 6.635 7.879
扩展练习
1.想要检验是否喜欢参加体育活动是不是与性别有关,应该检验( )
A.H0:男性喜欢参加体育活动
B.H0:女性不喜欢参加体育活动
C.H0:喜欢参加体育活动与性别有关
D.H0:喜欢参加体育活动与性别无关
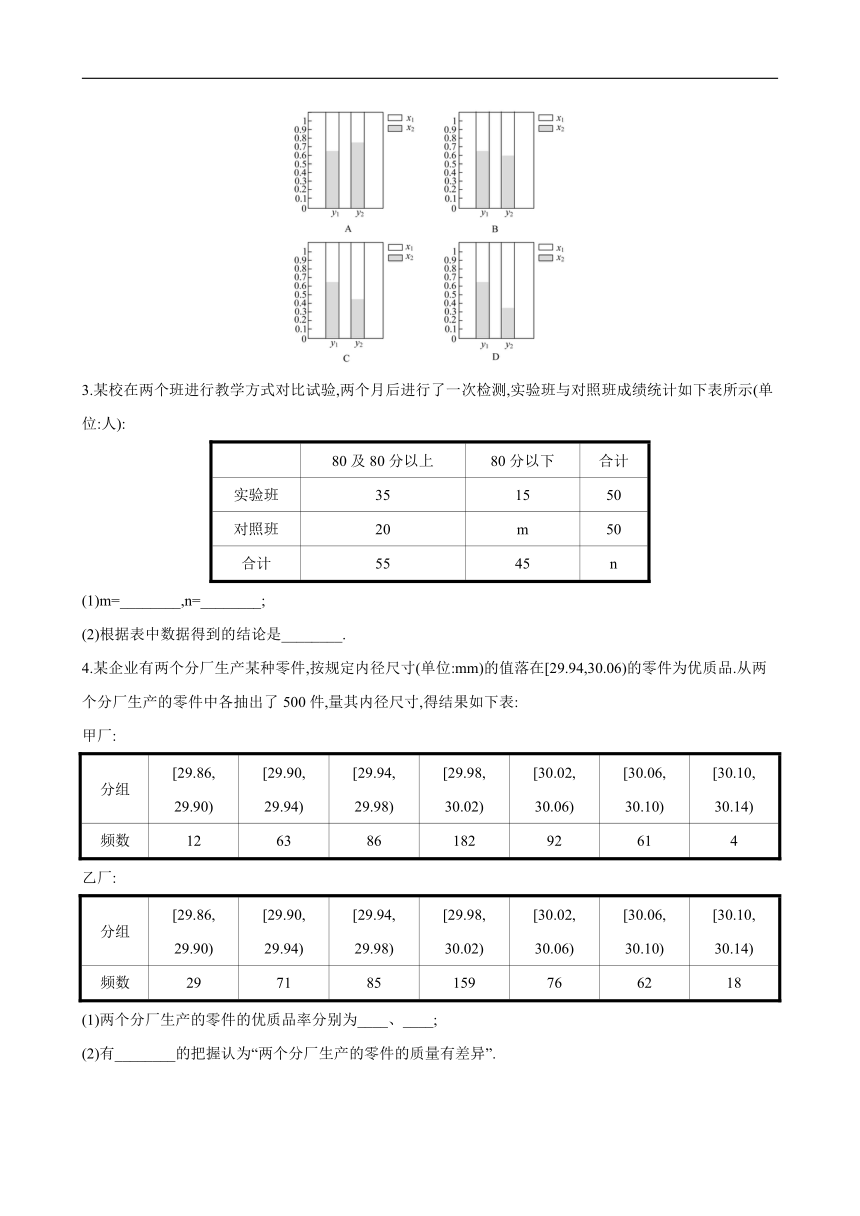
2.用等高条形图粗略估计两个分类变量是否相关,观察下列各图,其中两个分类变量关系最强的是( )
3.某校在两个班进行教学方式对比试验,两个月后进行了一次检测,实验班与对照班成绩统计如下表所示(单位:人):
80及80分以上 80分以下 合计
实验班 35 15 50
对照班 20 m 50
合计 55 45 n
(1)m=________,n=________;?
(2)根据表中数据得到的结论是________.?
4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 12 63 86 182 92 61 4
乙厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 29 71 85 159 76 62 18
(1)两个分厂生产的零件的优质品率分别为____、____;?
(2)有________的把握认为“两个分厂生产的零件的质量有差异”.?
5.近年电子商务蓬勃发展,2020年某网购平台“双11”一天的销售业绩高达1 682亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.
(1)根据已知条件完成下面的2×2列联表,并回答能否在犯错误的概率不超过0.01的前提下认为“网购者对商品满意与对快递满意之间有关系”.
对快递满意 对快递不满意 合计
对商品满意 80
对商品不满意
合计
200
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.
附:χ2=(其中n=a+b+c+d为样本容量)
P(χ2≥xα) 0.10 0.05 0.025 0.010
xα 2.706 3.841 5.024 6.635
6.为调查某社区居民的业余生活状况,研究这一社区居民在20:00~22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
看电视 看书 合计
男 10 50 60
女 10 10 20
合计 20 60 80
(1)根据以上数据,能否在犯错误的概率不超过0.01的前提下认为“在20:00~22:00时间段居民的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,在该社区的所有男性中随机调查3人,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的数学期望和方差.
参考答案
1.为考察A,B两种药物预防某疾病的效果,进行动物试验,分别得到如下等高条形图:
根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物B的预防效果优于药物A的预防效果
B.药物A的预防效果优于药物B的预防效果
C.药物A,B对该疾病均有显著的预防效果
D.药物A,B对该疾病均没有预防效果
分析:选B.从等高条形图可以看出,服用药物A后未患病的比例比服用药物B后未患病的比例大得多,预防效果更好.
2.(多选题)下列说法正确的是( )
A.事件A与B独立,即两个事件互不影响
B.事件A与B关系越密切,则χ2就越大
C.χ2的大小是判定事件A与B是否相关的唯一根据
D.若判定两事件A与B相关,则A发生B一定发生
分析:选AB.由事件的独立性知,A选项正确;由独立性检验的意义知,B选项正确;χ2的大小是判定事件A与B是否相关的一种方法,不是唯一依据,C选项不正确;若事件A与B相关,则A发生B可能发生,也可能不发生,D选项不正确.
3.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )
表1
不及格 及格 合计
男 6 14 20
女 10 22 32
合计 16 36 52
表2
好 差 合计
男 4 16 20
女 12 20 32
合计 16 36 52
表3
偏高 正常 合计
男 8 12 20
女 8 24 32
合计 16 36 52
表4
丰富 不丰富 合计
男 14 6 20
女 2 30 32
合计 16 36 52
A.成绩 B.视力 C.智商 D.阅读量
分析:选D.因为=
=,
==,
==,
==,
则有>>>,
所以阅读量与性别有关联的可能性最大.
4.有两个分类变量X,Y,其列联表如下所示,
Y1 Y2
X1 a 20-a
X2 15-a 30+a
其中a,15-a均为大于5的整数,若在犯错误的概率不超过0.05的前提下认为X,Y有关,则a的值为( )
A.8 B.9 C.8或9 D.6或8
分析:选C.根据公式,得
χ2=
=>3.841,根据a>5且15-a>5,a∈Z,求得当a=8或9时满足题意.
5.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算χ2=7.63,根据这一数据分析,是否有99.9%的把握说,打鼾与患心脏病是有关的:________.(填“是”或“否”)?
分析:因为χ2=7.63<10.828=x0.001,
因此,没有99.9%的把握说,打鼾与患心脏病是有关的.
答案:否
6.如果根据性别与是否爱好运动的列联表得到χ2≈3.852>3.841,则判断性别与是否爱好运动有关,那么这种判断犯错误的可能性不超过________.?
分析:因为P(χ2≥3.841)≈0.05.
所以判断性别与是否爱好运动有关,出错的可能性不超过5%.
答案:5%
7.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共60人,患胃病者生活规律的共20人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共200人.
(1)根据以上数据列出2×2列联表;
(2)在犯错误的概率不超过0.01的前提下能否认为40岁以上的人患胃病与否和生活规律有关系?为什么?
分析:(1)由已知可列2×2列联表:
患胃病 未患胃病 合计
生活规律 20 200 220
生活不规律 60 260 320
合计 80 460 540
(2)根据列联表中的数据,由计算公式得
χ2=≈9.638>6.635=x0.01,
因此在犯错误的概率不超过0.01的前提下认为40岁以上的人患胃病与否和生活规律有关.
8.“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1)写出2×2列联表;
(2)能否在犯错误的概率不超过0.1的前提下认为猜对歌曲名称与年龄有关系?说明你的理由.(下面的临界值表供参考)
α 0.1 0.05 0.01 0.005
xα 2.706 3.841 6.635 7.879
分析:(1)根据所给的二维条形图得到列联表:
正确 错误 合计
20~30岁 10 30 40
30~40岁 10 70 80
合计 20 100 120
(2)根据列联表所给的数据计算得χ2==3>2.706=x0.1,
所以在犯错误的概率不超过0.1的前提下认为猜对歌曲名称与年龄有关系.
扩展练习
1.想要检验是否喜欢参加体育活动是不是与性别有关,应该检验( )
A.H0:男性喜欢参加体育活动
B.H0:女性不喜欢参加体育活动
C.H0:喜欢参加体育活动与性别有关
D.H0:喜欢参加体育活动与性别无关
分析:选D.独立性检验假设有反证法的意味,应假设两类变量(而非变量的属性)无关,这时的χ2应该很小,如果χ2很大,则可以否定假设,如果χ2很小,则不能够肯定或者否定假设.
2.用等高条形图粗略估计两个分类变量是否相关,观察下列各图,其中两个分类变量关系最强的是( )
分析:选D.由等高条形图易知,D选项两个分类变量关系最强.
3.某校在两个班进行教学方式对比试验,两个月后进行了一次检测,实验班与对照班成绩统计如下表所示(单位:人):
80及80分以上 80分以下 合计
实验班 35 15 50
对照班 20 m 50
合计 55 45 n
(1)m=________,n=________;?
(2)根据表中数据得到的结论是________.?
分析:(1)m=45-15=30,n=50+50=100.
(2)由表中的数据得χ2=≈9.091.因为9.091>7.879,
所以有99.5%的把握说“教学方式与成绩有关系”.
答案:(1)30 100
(2)有99.5%的把握说“教学方式与成绩有关系”
4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 12 63 86 182 92 61 4
乙厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 29 71 85 159 76 62 18
(1)两个分厂生产的零件的优质品率分别为____、____;?
(2)有________的把握认为“两个分厂生产的零件的质量有差异”.?
分析:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为=64%.
(2)
甲厂 乙厂 合计
优质品 360 320 680
非优质品 140 180 320
合计 500 500 1 000
χ2=≈7.35>6.635,
所以有99%的把握认为“两个分厂生产的零件的质量有差异”.
答案:(1)72% 64% (2)99%
5.近年电子商务蓬勃发展,2020年某网购平台“双11”一天的销售业绩高达1 682亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.
(1)根据已知条件完成下面的2×2列联表,并回答能否在犯错误的概率不超过0.01的前提下认为“网购者对商品满意与对快递满意之间有关系”.
对快递满意 对快递不满意 合计
对商品满意 80
对商品不满意
合计
200
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.
附:χ2=(其中n=a+b+c+d为样本容量)
P(χ2≥xα) 0.10 0.05 0.025 0.010
xα 2.706 3.841 5.024 6.635
分析:(1)2×2列联表:
对快递满意 对快递不满意 合计
对商品满意 80 60 140
对商品不满意 40 20 60
合计 120 80 200
χ2=≈1.59,
由于1.59<6.635=x0.01,
所以不能在犯错误的概率不超过0.01的前提下认为“网购者对商品满意与对快递满意之间有关系”.
(2)根据题意,抽取的10次交易中,对商品和快递都满意的交易有4次,记为A,B,C,D,其余6次不是都满意的交易记为123456.那么抽取2次交易一共有45种可能:AB,AC,AD,A1,A2,A3,A4,A5,A6,BC,BD,B1,B2,……,56.其中2次交易对商品和快递不是都满意的有15种:12,13,……,56.
所以在抽取的2次交易中,至少一次对商品和快递都满意的概率是P==.
6.为调查某社区居民的业余生活状况,研究这一社区居民在20:00~22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
看电视 看书 合计
男 10 50 60
女 10 10 20
合计 20 60 80
(1)根据以上数据,能否在犯错误的概率不超过0.01的前提下认为“在20:00~22:00时间段居民的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,在该社区的所有男性中随机调查3人,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的数学期望和方差.
分析:(1)根据2×2列联表得,χ2=≈8.889>6.635,
所以能在犯错误的概率不超过0.01的前提下认为“在20:00~22:00时间段居民的休闲方式与性别有关系”.
(2)由题意得X~B,
E(X)=3×=,D(X)=3××=.
1.为考察A,B两种药物预防某疾病的效果,进行动物试验,分别得到如下等高条形图:
根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物B的预防效果优于药物A的预防效果
B.药物A的预防效果优于药物B的预防效果
C.药物A,B对该疾病均有显著的预防效果
D.药物A,B对该疾病均没有预防效果
2.(多选题)下列说法正确的是( )
A.事件A与B独立,即两个事件互不影响
B.事件A与B关系越密切,则χ2就越大
C.χ2的大小是判定事件A与B是否相关的唯一根据
D.若判定两事件A与B相关,则A发生B一定发生
3.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )
表1
不及格 及格 合计
男 6 14 20
女 10 22 32
合计 16 36 52
表2
好 差 合计
男 4 16 20
女 12 20 32
合计 16 36 52
表3
偏高 正常 合计
男 8 12 20
女 8 24 32
合计 16 36 52
表4
丰富 不丰富 合计
男 14 6 20
女 2 30 32
合计 16 36 52
A.成绩 B.视力 C.智商 D.阅读量
4.有两个分类变量X,Y,其列联表如下所示,
Y1 Y2
X1 a 20-a
X2 15-a 30+a
其中a,15-a均为大于5的整数,若在犯错误的概率不超过0.05的前提下认为X,Y有关,则a的值为( )
A.8 B.9 C.8或9 D.6或8
5.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算χ2=7.63,根据这一数据分析,是否有99.9%的把握说,打鼾与患心脏病是有关的:________.(填“是”或“否”)?
6.如果根据性别与是否爱好运动的列联表得到χ2≈3.852>3.841,则判断性别与是否爱好运动有关,那么这种判断犯错误的可能性不超过________.?
7.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共60人,患胃病者生活规律的共20人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共200人.
(1)根据以上数据列出2×2列联表;
(2)在犯错误的概率不超过0.01的前提下能否认为40岁以上的人患胃病与否和生活规律有关系?为什么?
8.“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1)写出2×2列联表;
(2)能否在犯错误的概率不超过0.1的前提下认为猜对歌曲名称与年龄有关系?说明你的理由.(下面的临界值表供参考)
α 0.1 0.05 0.01 0.005
xα 2.706 3.841 6.635 7.879
扩展练习
1.想要检验是否喜欢参加体育活动是不是与性别有关,应该检验( )
A.H0:男性喜欢参加体育活动
B.H0:女性不喜欢参加体育活动
C.H0:喜欢参加体育活动与性别有关
D.H0:喜欢参加体育活动与性别无关
2.用等高条形图粗略估计两个分类变量是否相关,观察下列各图,其中两个分类变量关系最强的是( )
3.某校在两个班进行教学方式对比试验,两个月后进行了一次检测,实验班与对照班成绩统计如下表所示(单位:人):
80及80分以上 80分以下 合计
实验班 35 15 50
对照班 20 m 50
合计 55 45 n
(1)m=________,n=________;?
(2)根据表中数据得到的结论是________.?
4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 12 63 86 182 92 61 4
乙厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 29 71 85 159 76 62 18
(1)两个分厂生产的零件的优质品率分别为____、____;?
(2)有________的把握认为“两个分厂生产的零件的质量有差异”.?
5.近年电子商务蓬勃发展,2020年某网购平台“双11”一天的销售业绩高达1 682亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.
(1)根据已知条件完成下面的2×2列联表,并回答能否在犯错误的概率不超过0.01的前提下认为“网购者对商品满意与对快递满意之间有关系”.
对快递满意 对快递不满意 合计
对商品满意 80
对商品不满意
合计
200
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.
附:χ2=(其中n=a+b+c+d为样本容量)
P(χ2≥xα) 0.10 0.05 0.025 0.010
xα 2.706 3.841 5.024 6.635
6.为调查某社区居民的业余生活状况,研究这一社区居民在20:00~22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
看电视 看书 合计
男 10 50 60
女 10 10 20
合计 20 60 80
(1)根据以上数据,能否在犯错误的概率不超过0.01的前提下认为“在20:00~22:00时间段居民的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,在该社区的所有男性中随机调查3人,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的数学期望和方差.
参考答案
1.为考察A,B两种药物预防某疾病的效果,进行动物试验,分别得到如下等高条形图:
根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物B的预防效果优于药物A的预防效果
B.药物A的预防效果优于药物B的预防效果
C.药物A,B对该疾病均有显著的预防效果
D.药物A,B对该疾病均没有预防效果
分析:选B.从等高条形图可以看出,服用药物A后未患病的比例比服用药物B后未患病的比例大得多,预防效果更好.
2.(多选题)下列说法正确的是( )
A.事件A与B独立,即两个事件互不影响
B.事件A与B关系越密切,则χ2就越大
C.χ2的大小是判定事件A与B是否相关的唯一根据
D.若判定两事件A与B相关,则A发生B一定发生
分析:选AB.由事件的独立性知,A选项正确;由独立性检验的意义知,B选项正确;χ2的大小是判定事件A与B是否相关的一种方法,不是唯一依据,C选项不正确;若事件A与B相关,则A发生B可能发生,也可能不发生,D选项不正确.
3.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系,随机抽查了52名中学生,得到统计数据如表1至表4,则与性别有关联的可能性最大的变量是( )
表1
不及格 及格 合计
男 6 14 20
女 10 22 32
合计 16 36 52
表2
好 差 合计
男 4 16 20
女 12 20 32
合计 16 36 52
表3
偏高 正常 合计
男 8 12 20
女 8 24 32
合计 16 36 52
表4
丰富 不丰富 合计
男 14 6 20
女 2 30 32
合计 16 36 52
A.成绩 B.视力 C.智商 D.阅读量
分析:选D.因为=
=,
==,
==,
==,
则有>>>,
所以阅读量与性别有关联的可能性最大.
4.有两个分类变量X,Y,其列联表如下所示,
Y1 Y2
X1 a 20-a
X2 15-a 30+a
其中a,15-a均为大于5的整数,若在犯错误的概率不超过0.05的前提下认为X,Y有关,则a的值为( )
A.8 B.9 C.8或9 D.6或8
分析:选C.根据公式,得
χ2=
=>3.841,根据a>5且15-a>5,a∈Z,求得当a=8或9时满足题意.
5.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算χ2=7.63,根据这一数据分析,是否有99.9%的把握说,打鼾与患心脏病是有关的:________.(填“是”或“否”)?
分析:因为χ2=7.63<10.828=x0.001,
因此,没有99.9%的把握说,打鼾与患心脏病是有关的.
答案:否
6.如果根据性别与是否爱好运动的列联表得到χ2≈3.852>3.841,则判断性别与是否爱好运动有关,那么这种判断犯错误的可能性不超过________.?
分析:因为P(χ2≥3.841)≈0.05.
所以判断性别与是否爱好运动有关,出错的可能性不超过5%.
答案:5%
7.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共60人,患胃病者生活规律的共20人,未患胃病者生活不规律的共260人,未患胃病者生活规律的共200人.
(1)根据以上数据列出2×2列联表;
(2)在犯错误的概率不超过0.01的前提下能否认为40岁以上的人患胃病与否和生活规律有关系?为什么?
分析:(1)由已知可列2×2列联表:
患胃病 未患胃病 合计
生活规律 20 200 220
生活不规律 60 260 320
合计 80 460 540
(2)根据列联表中的数据,由计算公式得
χ2=≈9.638>6.635=x0.01,
因此在犯错误的概率不超过0.01的前提下认为40岁以上的人患胃病与否和生活规律有关.
8.“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1)写出2×2列联表;
(2)能否在犯错误的概率不超过0.1的前提下认为猜对歌曲名称与年龄有关系?说明你的理由.(下面的临界值表供参考)
α 0.1 0.05 0.01 0.005
xα 2.706 3.841 6.635 7.879
分析:(1)根据所给的二维条形图得到列联表:
正确 错误 合计
20~30岁 10 30 40
30~40岁 10 70 80
合计 20 100 120
(2)根据列联表所给的数据计算得χ2==3>2.706=x0.1,
所以在犯错误的概率不超过0.1的前提下认为猜对歌曲名称与年龄有关系.
扩展练习
1.想要检验是否喜欢参加体育活动是不是与性别有关,应该检验( )
A.H0:男性喜欢参加体育活动
B.H0:女性不喜欢参加体育活动
C.H0:喜欢参加体育活动与性别有关
D.H0:喜欢参加体育活动与性别无关
分析:选D.独立性检验假设有反证法的意味,应假设两类变量(而非变量的属性)无关,这时的χ2应该很小,如果χ2很大,则可以否定假设,如果χ2很小,则不能够肯定或者否定假设.
2.用等高条形图粗略估计两个分类变量是否相关,观察下列各图,其中两个分类变量关系最强的是( )
分析:选D.由等高条形图易知,D选项两个分类变量关系最强.
3.某校在两个班进行教学方式对比试验,两个月后进行了一次检测,实验班与对照班成绩统计如下表所示(单位:人):
80及80分以上 80分以下 合计
实验班 35 15 50
对照班 20 m 50
合计 55 45 n
(1)m=________,n=________;?
(2)根据表中数据得到的结论是________.?
分析:(1)m=45-15=30,n=50+50=100.
(2)由表中的数据得χ2=≈9.091.因为9.091>7.879,
所以有99.5%的把握说“教学方式与成绩有关系”.
答案:(1)30 100
(2)有99.5%的把握说“教学方式与成绩有关系”
4.某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 12 63 86 182 92 61 4
乙厂:
分组 [29.86,
29.90) [29.90,
29.94) [29.94,
29.98) [29.98,
30.02) [30.02,
30.06) [30.06,
30.10) [30.10,
30.14)
频数 29 71 85 159 76 62 18
(1)两个分厂生产的零件的优质品率分别为____、____;?
(2)有________的把握认为“两个分厂生产的零件的质量有差异”.?
分析:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为=72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为=64%.
(2)
甲厂 乙厂 合计
优质品 360 320 680
非优质品 140 180 320
合计 500 500 1 000
χ2=≈7.35>6.635,
所以有99%的把握认为“两个分厂生产的零件的质量有差异”.
答案:(1)72% 64% (2)99%
5.近年电子商务蓬勃发展,2020年某网购平台“双11”一天的销售业绩高达1 682亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.70,对快递的满意率为0.60,其中对商品和快递都满意的交易为80次.
(1)根据已知条件完成下面的2×2列联表,并回答能否在犯错误的概率不超过0.01的前提下认为“网购者对商品满意与对快递满意之间有关系”.
对快递满意 对快递不满意 合计
对商品满意 80
对商品不满意
合计
200
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取10次交易进行问卷调查,详细了解满意与否的具体原因,并在这10次交易中再随机抽取2次进行电话回访,听取购物者意见.求电话回访的2次交易至少有一次对商品和快递都满意的概率.
附:χ2=(其中n=a+b+c+d为样本容量)
P(χ2≥xα) 0.10 0.05 0.025 0.010
xα 2.706 3.841 5.024 6.635
分析:(1)2×2列联表:
对快递满意 对快递不满意 合计
对商品满意 80 60 140
对商品不满意 40 20 60
合计 120 80 200
χ2=≈1.59,
由于1.59<6.635=x0.01,
所以不能在犯错误的概率不超过0.01的前提下认为“网购者对商品满意与对快递满意之间有关系”.
(2)根据题意,抽取的10次交易中,对商品和快递都满意的交易有4次,记为A,B,C,D,其余6次不是都满意的交易记为123456.那么抽取2次交易一共有45种可能:AB,AC,AD,A1,A2,A3,A4,A5,A6,BC,BD,B1,B2,……,56.其中2次交易对商品和快递不是都满意的有15种:12,13,……,56.
所以在抽取的2次交易中,至少一次对商品和快递都满意的概率是P==.
6.为调查某社区居民的业余生活状况,研究这一社区居民在20:00~22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
看电视 看书 合计
男 10 50 60
女 10 10 20
合计 20 60 80
(1)根据以上数据,能否在犯错误的概率不超过0.01的前提下认为“在20:00~22:00时间段居民的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,在该社区的所有男性中随机调查3人,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的数学期望和方差.
分析:(1)根据2×2列联表得,χ2=≈8.889>6.635,
所以能在犯错误的概率不超过0.01的前提下认为“在20:00~22:00时间段居民的休闲方式与性别有关系”.
(2)由题意得X~B,
E(X)=3×=,D(X)=3××=.
