第八章成对数据的统计分析测试题2020-2021学年高二数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析
文档属性
| 名称 | 第八章成对数据的统计分析测试题2020-2021学年高二数学人教A版(2019)选择性必修第三册第八章成对数据的统计分析 |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 16:56:44 | ||
图片预览




文档简介
第八章测试题
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列两个量之间的关系是相关关系的为( )
A.匀速直线运动的物体时间与位移的关系
B.学生的成绩和体重
C.路上酒后驾驶的人数和交通事故发生的多少
D.水的体积和重量
2.如图2×2列联表中a,b的值分别为( )
Y1 Y2 总计
X1 c a e
X2 23 d 48
总计 b 78 121
A.54,43 B.53,43
C.53,42 D.54,42
3.根据如下样本数据:
x 3 4 5 6 7 8
y 4 2.5 -0.5 0.5 -2 -3
得到的回归直线方程为=x+,则( )
A.>0,<0 B.>0,>0
C.<0,>0 D.<0,<0
4.设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的斜率是b,纵轴上的截距是a,那么必有( )
A.b与r的符号相同 B.a与r的符号相同
C.b与r的符号相反 D.a与r的符号相反
5.对某同学7次考试的数学成绩x和物理成绩y进行分析,下面是该生7次考试的成绩.
数学 88 83 117 92 108 100 112
物理 94 91 108 96 104 101 106
发现他的物理成绩y与数学成绩x是线性相关的,利用最小二乘法得到线性回归方程为=0.5x+a,若该生的数学成绩达到130分,估计他的物理成绩大约是
( )
A.114.5 B.115 C.115.5 D.116
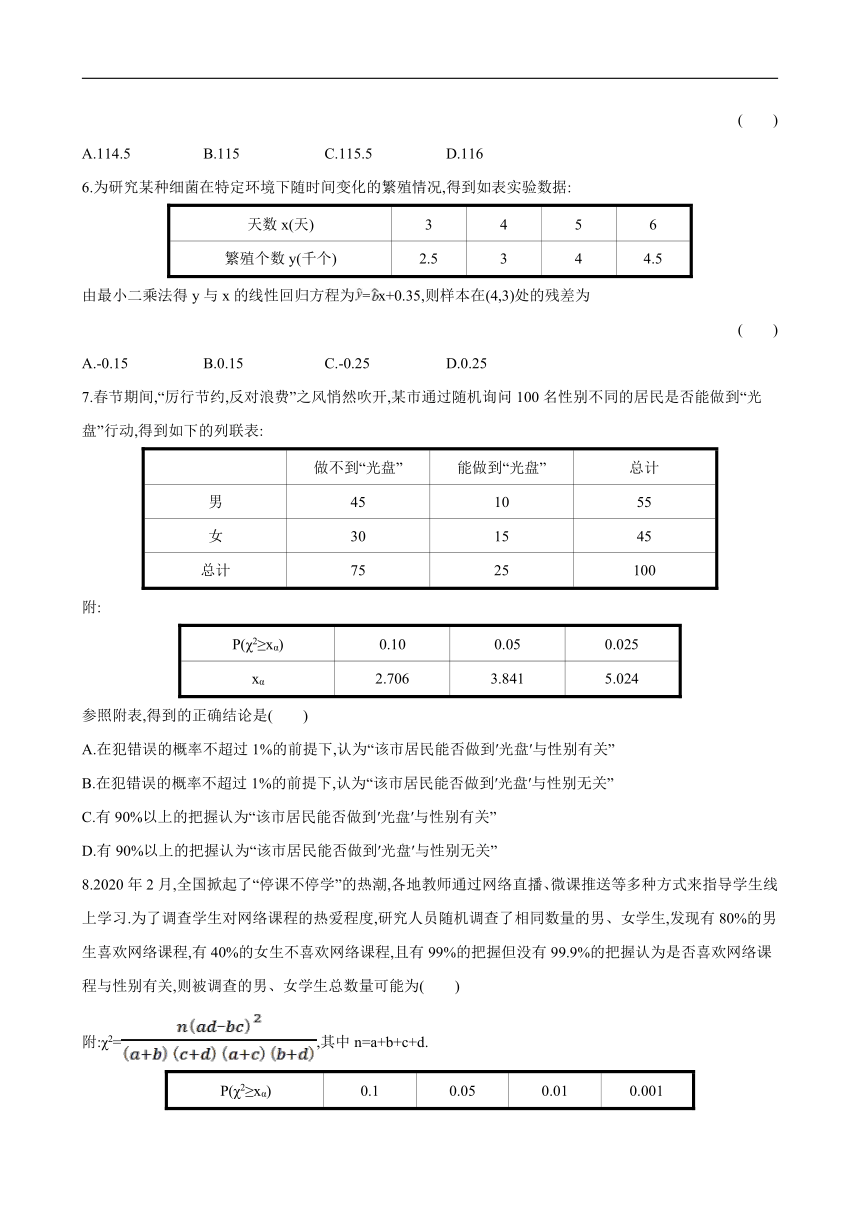
6.为研究某种细菌在特定环境下随时间变化的繁殖情况,得到如表实验数据:
天数x(天) 3 4 5 6
繁殖个数y(千个) 2.5 3 4 4.5
由最小二乘法得y与x的线性回归方程为=x+0.35,则样本在(4,3)处的残差为
( )
A.-0.15 B.0.15 C.-0.25 D.0.25
7.春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘” 总计
男 45 10 55
女 30 15 45
总计 75 25 100
附:
P(χ2≥xα) 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别无关”
C.有90%以上的把握认为“该市居民能否做到′光盘′与性别有关”
D.有90%以上的把握认为“该市居民能否做到′光盘′与性别无关”
8.2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有80%的男生喜欢网络课程,有40%的女生不喜欢网络课程,且有99%的把握但没有99.9%的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥xα) 0.1 0.05 0.01 0.001
xα 2.706 3.841 6.635 10.828
A.130 B.190 C.240 D.250
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.对于回归直线方程=x+,下列说法正确的是( )
A.直线必经过点(,)
B.x增加1个单位时,y平均增加个单位
C.样本数据中x=0时,可能有y=
D.样本数据中x=0时,一定有y=
10.根据下面的2×2列联表得到如下,4个判断正确的为( )
嗜酒 不嗜酒 总计
患肝病 700 60 760
未患肝病 200 32 232
总计 900 92 992
A.至少有99.9%的把握认为“患肝病与嗜酒有关”
B.至少有99%的把握认为“患肝病与嗜酒有关”
C.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关”
D.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒无关”
11.对两个变量x与y进行线性相关性和回归效果分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法正确的是( )
A.残差平方和越小的模型,拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心(,)
C.若变量x与y之间的相关系数r=0.80,则变量x与y之间具有很强的线性相关性
D.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
12.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在A地区的100天日落和夜晚天气,得到如下2×2列联表:
下雨 未下雨
出现 25 5
未出现 25 45
临界值表
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
并计算得到χ2≈19.05,下列小波对A地区天气判断正确的是( )
A.夜晚下雨的概率约为
B.未出现“日落云里走”夜晚下雨的概率约为
C.有99.9%的把握认为“′日落云里走′是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有99.9%的把握认为夜晚会下雨
三、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.如表提供的x和y是两组具有线性相关关系的数据,已知其回归方程为=0.65x+0.6,则m=________.?
x 3 5 7 9
y 2.5 4 m 6.5
14.某高校有10 000名学生,其中女生3 000名,男生7 000名.为调查爱好体育运动是否与性别有关,用分层抽样的方法抽取120名学生,制成独立性检验的2×2列表如表,则a-b=________.(用数字作答)?
男 女 合计
爱好体育运动 a 9 ####
不爱好体育运动 28 b ####
合计 #### #### 120
15.若对甲、乙、丙3组不同的数据作线性相关性检验,得到这3组数据的线性相关系数依次为0.93,0.42,-0.95,则线性相关程度最强的一组是________.(填甲、乙、丙中的一个)?
16.某产品在某零售摊位上的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如表所示:
x 16 17 18 19
y 50 44 41 31
由上表可得回归直线方程=x+中的=-6,则=__________,据此模型预计零售价定为15元时,每天的销售量为________.(第1空2分,第2空3分)?
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(10分)针对某新型病毒,某科研机构已研发出甲、乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占.
(1)根据题中数据,完成下面的列联表;
产生抗体 未产生抗体 合计
甲
乙
合计
(2)根据(1)中的列联表,判断能否有95%的把握认为甲、乙两种疫苗的效果有差异.
参考公式:χ2=,其中n=a+b+c+d.
参考数据:
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
18.(12分)在3+1+2的新高考模式下,某学校计划在高一下学期开设“物理”和“历史”两个选修科目.为了了解学生对这两个科目的选课意向,以便提前规划教育资源,教务处从高一年级500名学生(其中男生200人,女生300人)中,采用分层抽样的方法从中抽取部分学生进行调查.其中,女生比男生多抽取20人.
(1)请问总共抽取了多少名学生进行调查;
(2)新高考模式要求每名学生在“物理”和“历史”这两个科目中必须选择一个科目且只能选择一个科目,下表是根据调查结果得到的一个不完整的列联表,请将下面的列联表补充完整,并判断是否有99.9%的把握认为选择科目与性别有关?
选择“物理” 选择“历史” 总计
男生
女生 25
总计 55
附:χ2=,n=a+b+c+d.
P(χ2≥xα) 0.05 0.01 0.005 0.001
xα 3.841 6.635 7.879 10.828
19.(12分)为了了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如表:
患心肺疾病 不患心肺疾病 总计
大于40岁 16
小于等于40岁
12
总计
40
已知在40人中随机抽取1人,抽到不患心肺疾病的市民的概率为.
(1)请将2×2列联表补充完整;
(2)已知在大于40岁且患心肺疾病的市民中,有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出2人,记需住院治疗的人数为ξ,求ξ的分布列和数学期望;
(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
20.(12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得xi=60,yi=1 200,
(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
21.(12分)PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 周一 周二 周三 周四 周五
车流量x(万辆) 50 51 54 57 58
PM2.5的浓度y (微克/立方米) 69 70 74 78 79
(1)请根据表格数据,在如图所示的平面直角坐标系中画出散点图;
(2)根据表格数据,用最小二乘法求出y关于x的回归直线方程=x+;
(3)若周六同一时间的车流量是25万辆,试根据(2)中求出的回归直线方程预测此时PM2.5的浓度为多少(保留整数).
22.(12分)某城市9年前分别同时开始建设物流城和湿地公园,物流城3年建设完成,建成后若年投入x亿元,该年产生的经济净效益为(2ln x+5)亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为(x+3)亿元.
(1)对湿地公园,请在x=kn+b,x=kn2+b中选择一个合适模型,求投入额x与投入年份n的回归方程;
(2)从建设开始的第10年,若对物流城投入0.25亿元,预测这一年物流城和湿地公园哪个产生的年经济净效益高?请说明理由.
参考数据及公式:=0.336,nixi=6.22;当t=n2时,=11,=979,回归方程中的tixi=29.7;回归方程=s+斜率与截距=,=-s.
参考答案
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列两个量之间的关系是相关关系的为( )
A.匀速直线运动的物体时间与位移的关系
B.学生的成绩和体重
C.路上酒后驾驶的人数和交通事故发生的多少
D.水的体积和重量
分析:选C.由匀速直线运动的物体时间与位移的关系公式知,是确定的函数关系,故A不对;学生的成绩和体重没有什么关系,故B不对;路上酒后驾驶的人数会影响交通事故发生的多少,但不是唯一因素,它们之间有相关性,故C对;水的体积V和重量x的关系为:V=k·x,是确定的函数关系,故D不对.
2.如图2×2列联表中a,b的值分别为( )
Y1 Y2 总计
X1 c a e
X2 23 d 48
总计 b 78 121
A.54,43 B.53,43
C.53,42 D.54,42
分析:选B.由2×2列联表可知,d=48-23=25,e=121-48=73,
所以a=78-d=78-25=53,c=e-a=73-53=20,
所以b=c+23=43.
3.根据如下样本数据:
x 3 4 5 6 7 8
y 4 2.5 -0.5 0.5 -2 -3
得到的回归直线方程为=x+,则( )
A.>0,<0 B.>0,>0
C.<0,>0 D.<0,<0
分析:选A.根据题意,画出散点图.
根据散点图,知两个变量为负相关,且回归直线与y轴的交点在y轴正半轴,
所以>0,<0.
4.设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的斜率是b,纵轴上的截距是a,那么必有( )
A.b与r的符号相同 B.a与r的符号相同
C.b与r的符号相反 D.a与r的符号相反
分析:选A.因为b>0时,两变量正相关,此时r>0;b<0时,两变量负相关,此时r<0.
5.对某同学7次考试的数学成绩x和物理成绩y进行分析,下面是该生7次考试的成绩.
数学 88 83 117 92 108 100 112
物理 94 91 108 96 104 101 106
发现他的物理成绩y与数学成绩x是线性相关的,利用最小二乘法得到线性回归方程为=0.5x+a,若该生的数学成绩达到130分,估计他的物理成绩大约是
( )
A.114.5 B.115 C.115.5 D.116
分析:选B.由题意可知
==100,
==100,
因为回归直线经过样本中心,
所以100=0.5×100+a,解得a=50,
线性回归方程为=0.5x+50,
该生的数学成绩达到130分,估计他的物理成绩大约是:0.5×130+50=115.
6.为研究某种细菌在特定环境下随时间变化的繁殖情况,得到如表实验数据:
天数x(天) 3 4 5 6
繁殖个数y(千个) 2.5 3 4 4.5
由最小二乘法得y与x的线性回归方程为=x+0.35,则样本在(4,3)处的残差为
( )
A.-0.15 B.0.15 C.-0.25 D.0.25
分析:选A.因为=×(3+4+5+6)=4.5,
=(2.5+3+4+4.5)=3.5,
因为回归直线经过样本中心,所以3.5=4.5+0.35,
解得=0.7,
线性回归方程为=0.7x+0.35,
x=4时,=0.7×4+0.35=3.15.
所以样本在(4,3)处的残差为:3-3.15=-0.15.
7.春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘” 总计
男 45 10 55
女 30 15 45
总计 75 25 100
附:
P(χ2≥xα) 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别无关”
C.有90%以上的把握认为“该市居民能否做到′光盘′与性别有关”
D.有90%以上的把握认为“该市居民能否做到′光盘′与性别无关”
分析:选C.由公式可计算
χ2=≈3.03>2.706,
所以有90%以上的把握认为“该市居民能否做到′光盘′与性别有关”.
8.2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有80%的男生喜欢网络课程,有40%的女生不喜欢网络课程,且有99%的把握但没有99.9%的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥xα) 0.1 0.05 0.01 0.001
xα 2.706 3.841 6.635 10.828
A.130 B.190 C.240 D.250
分析:选B.依题意,设男、女生的人数各为5x,建立2×2列联表如表所示:
喜欢网络课程 不喜欢网络课程 总计
男生 4x x 5x
女生 3x 2x 5x
总计 7x 3x 10x
故χ2==,由题可知6.635<<10.828,
所以139.335<10x<227.388.只有B符合题意.
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.对于回归直线方程=x+,下列说法正确的是( )
A.直线必经过点(,)
B.x增加1个单位时,y平均增加个单位
C.样本数据中x=0时,可能有y=
D.样本数据中x=0时,一定有y=
分析:选ABC.回归直线方程是根据样本数据得到的一个近似曲线,故由它得到的值也是一个近似值,D选项错误,其他选项均正确.
10.根据下面的2×2列联表得到如下,4个判断正确的为( )
嗜酒 不嗜酒 总计
患肝病 700 60 760
未患肝病 200 32 232
总计 900 92 992
A.至少有99.9%的把握认为“患肝病与嗜酒有关”
B.至少有99%的把握认为“患肝病与嗜酒有关”
C.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关”
D.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒无关”
分析:选BC.由2×2列联表中数据可求得χ2=≈7.349>6.635,
所以在犯错误的概率不超过0.01的前提下,认为“患肝病与嗜酒有关”,
即至少有99%的把握认为“患肝病与嗜酒有关”.因此BC正确.
11.对两个变量x与y进行线性相关性和回归效果分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法正确的是( )
A.残差平方和越小的模型,拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心(,)
C.若变量x与y之间的相关系数r=0.80,则变量x与y之间具有很强的线性相关性
D.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
分析:选ABC.对两个变量x与y进行线性相关性和回归效果分析,得到一组样本数据.残差平方和越小的模型,拟合的效果越好,故A正确;由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心(,),故B正确;若变量x与y之间的相关系数r=0.80>0.75,则变量x与y之间具有很强的线性相关性,故C正确;用相关指数R2来刻画回归效果,R2越大,说明模型的拟合效果越好,故D错误.
12.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在A地区的100天日落和夜晚天气,得到如下2×2列联表:
下雨 未下雨
出现 25 5
未出现 25 45
临界值表
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
并计算得到χ2≈19.05,下列小波对A地区天气判断正确的是( )
A.夜晚下雨的概率约为
B.未出现“日落云里走”夜晚下雨的概率约为
C.有99.9%的把握认为“′日落云里走′是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有99.9%的把握认为夜晚会下雨
分析:选ABC.对于选项A:因为夜晚下雨的天数一共有25+25=50(天),所以夜晚下雨的概率约为=,故A正确;对于选项B:未出现“日落云里走”夜晚下雨的有25天,未出现“日落云里走”的一共25+45=70(天),所以未出现“日落云里走”夜晚下雨的概率约为=,故B正确;
对于选项C:因为χ2≈19.05>10.828,所以有99.9%的把握认为“‘日落云里走’′是否出现”与“当晚是否下雨”有关,故C正确,D错误.
三、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.如表提供的x和y是两组具有线性相关关系的数据,已知其回归方程为=0.65x+0.6,则m=________.?
x 3 5 7 9
y 2.5 4 m 6.5
分析:==6,==,
所以样本点的中心为,
代入=0.65x+0.6,得=0.65×6+0.6,
解得m=5.
答案:5
14.某高校有10 000名学生,其中女生3 000名,男生7 000名.为调查爱好体育运动是否与性别有关,用分层抽样的方法抽取120名学生,制成独立性检验的2×2列表如表,则a-b=________.(用数字作答)?
男 女 合计
爱好体育运动 a 9 ####
不爱好体育运动 28 b ####
合计 #### #### 120
分析:根据分层抽样原理,计算抽取男生120×=84(人),
女生120×=36(人),
所以a=84-28=56(人),b=36-9=27(人),
所以a-b=56-27=29(人).
答案:29
15.若对甲、乙、丙3组不同的数据作线性相关性检验,得到这3组数据的线性相关系数依次为0.93,0.42,-0.95,则线性相关程度最强的一组是________.(填甲、乙、丙中的一个)?
分析:两个变量y与x的回归模型中,它们的相关系数|r|越接近于1,这个模型的两个变量线性相关程度就越强,在甲、乙、丙中,所给的数值中-0.95的绝对值最接近1,所以丙的线性相关程度最强.
答案:丙
16.某产品在某零售摊位上的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如表所示:
x 16 17 18 19
y 50 44 41 31
由上表可得回归直线方程=x+中的=-6,则=__________,据此模型预计零售价定为15元时,每天的销售量为________.(第1空2分,第2空3分)?
分析:由题意知=17.5,=41.5,代入回归直线方程得=146.5,所以回归直线方程为=-6x+146.5,当x=15时,=146.5-15×6=56.5.
答案:146.5 56.5
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(10分)针对某新型病毒,某科研机构已研发出甲、乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占.
(1)根据题中数据,完成下面的列联表;
产生抗体 未产生抗体 合计
甲
乙
合计
(2)根据(1)中的列联表,判断能否有95%的把握认为甲、乙两种疫苗的效果有差异.
参考公式:χ2=,其中n=a+b+c+d.
参考数据:
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
分析:(1)由题意可得未产生该新型病毒抗体的志愿者的人数为100×=10,
则注射甲种疫苗的志愿者中未产生抗体的人数为10×=2,产生抗体的人数为50-2=48;
注射乙种疫苗的志愿者中未产生抗体的人数为10-2=8,产生抗体的人数为50-8=42.
产生抗体 未产生抗体 合计
甲 48 2 50
乙 42 8 50
合计 90 10 100
(2)计算χ2===4,
因为4>3.841,所以有95%的把握认为甲、乙两种疫苗的效果有差异.
18.(12分)在3+1+2的新高考模式下,某学校计划在高一下学期开设“物理”和“历史”两个选修科目.为了了解学生对这两个科目的选课意向,以便提前规划教育资源,教务处从高一年级500名学生(其中男生200人,女生300人)中,采用分层抽样的方法从中抽取部分学生进行调查.其中,女生比男生多抽取20人.
(1)请问总共抽取了多少名学生进行调查;
(2)新高考模式要求每名学生在“物理”和“历史”这两个科目中必须选择一个科目且只能选择一个科目,下表是根据调查结果得到的一个不完整的列联表,请将下面的列联表补充完整,并判断是否有99.9%的把握认为选择科目与性别有关?
选择“物理” 选择“历史” 总计
男生
女生 25
总计 55
附:χ2=,n=a+b+c+d.
P(χ2≥xα) 0.05 0.01 0.005 0.001
xα 3.841 6.635 7.879 10.828
分析:(1)设女生抽取x人,则男生抽取(x-20)人,
则x∶(x-20)=3∶2,解得x=60,
所以总共抽取了60+(60-20)=100(人).
(2)根据题意补充完整列联表如表.
选择“物理” 选择“历史” 总计
男生 30 10 40
女生 25 35 60
总计 55 45 100
由表中数据,
计算χ2==≈10.774<10.828,
所以没有99.9%的把握认为选择科目与性别有关.
19.(12分)为了了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如表:
患心肺疾病 不患心肺疾病 总计
大于40岁 16
小于等于40岁
12
总计
40
已知在40人中随机抽取1人,抽到不患心肺疾病的市民的概率为.
(1)请将2×2列联表补充完整;
(2)已知在大于40岁且患心肺疾病的市民中,有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出2人,记需住院治疗的人数为ξ,求ξ的分布列和数学期望;
(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
分析:(1)将2×2列联表补充完整:
患心肺疾病 不患心肺疾病 总计
大于40岁 16 4 20
小于等于40岁 8 12 20
总计 24 16 40
(2)ξ的可能取值为0,1,2.
P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,
所以随机变量ξ的分布列为
ξ 0 1 2
P
故ξ的数学期望E(ξ)=0×+1×+2×=.
(3)χ2==>6.635,
所以能在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关.
20.(12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得xi=60,yi=1 200,
(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
分析:(1)由已知,yi=1 200,
所以20个样区野生动物数量的平均数为yi=1 200=60,
所以该地区这种野生动物数量的估计值为60×200=12 000;
(2)因为(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800,
所以r====≈0.94;
(3)更合理的抽样方法是分层抽样,根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.
理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.
21.(12分)PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 周一 周二 周三 周四 周五
车流量x(万辆) 50 51 54 57 58
PM2.5的浓度y (微克/立方米) 69 70 74 78 79
(1)请根据表格数据,在如图所示的平面直角坐标系中画出散点图;
(2)根据表格数据,用最小二乘法求出y关于x的回归直线方程=x+;
(3)若周六同一时间的车流量是25万辆,试根据(2)中求出的回归直线方程预测此时PM2.5的浓度为多少(保留整数).
分析:(1)散点图如图.
(2)因为==54,
==74.
(xi-)(yi-)=4×5+3×4+3×4+4×5=64,
(xi-)2=(-4)2+(-3)2+32+42=50,
所以===1.28,
=-=74-1.28×54=4.88,
故y关于x的回归直线方程为=1.28x+4.88.
(3)当x=25时,y=1.28×25+4.88=36.88≈37,
所以可以预测此时PM2.5的浓度约为37微克/立方米.
22.(12分)某城市9年前分别同时开始建设物流城和湿地公园,物流城3年建设完成,建成后若年投入x亿元,该年产生的经济净效益为(2ln x+5)亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为(x+3)亿元.
(1)对湿地公园,请在x=kn+b,x=kn2+b中选择一个合适模型,求投入额x与投入年份n的回归方程;
(2)从建设开始的第10年,若对物流城投入0.25亿元,预测这一年物流城和湿地公园哪个产生的年经济净效益高?请说明理由.
参考数据及公式:=0.336,nixi=6.22;当t=n2时,=11,=979,回归方程中的tixi=29.7;回归方程=s+斜率与截距=,=-s.
分析:(1)根据散点图,应该选择模型x=kn2+b.
令t=n2,
则===0.03,
所以=-=0.336-0.03×11=0.006,
所以所求回归方程是=0.03t+0.006,即=0.03n2+0.006.
(2)若年投入x亿元,该年产生的经济净效益为(2ln x+5)亿元;即物流城第10年的年经济净效益为2ln 0.25+5=5-4ln 2亿元;根据回归方程可估计湿地公园第10年的投入约为0.03×62+0.006=1.086
亿元,该年的经济效益为1.086+3=4.086亿元.
因为4.086>5-4ln 2,
所以该年湿地公园产生的年经济净效益高.
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列两个量之间的关系是相关关系的为( )
A.匀速直线运动的物体时间与位移的关系
B.学生的成绩和体重
C.路上酒后驾驶的人数和交通事故发生的多少
D.水的体积和重量
2.如图2×2列联表中a,b的值分别为( )
Y1 Y2 总计
X1 c a e
X2 23 d 48
总计 b 78 121
A.54,43 B.53,43
C.53,42 D.54,42
3.根据如下样本数据:
x 3 4 5 6 7 8
y 4 2.5 -0.5 0.5 -2 -3
得到的回归直线方程为=x+,则( )
A.>0,<0 B.>0,>0
C.<0,>0 D.<0,<0
4.设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的斜率是b,纵轴上的截距是a,那么必有( )
A.b与r的符号相同 B.a与r的符号相同
C.b与r的符号相反 D.a与r的符号相反
5.对某同学7次考试的数学成绩x和物理成绩y进行分析,下面是该生7次考试的成绩.
数学 88 83 117 92 108 100 112
物理 94 91 108 96 104 101 106
发现他的物理成绩y与数学成绩x是线性相关的,利用最小二乘法得到线性回归方程为=0.5x+a,若该生的数学成绩达到130分,估计他的物理成绩大约是
( )
A.114.5 B.115 C.115.5 D.116
6.为研究某种细菌在特定环境下随时间变化的繁殖情况,得到如表实验数据:
天数x(天) 3 4 5 6
繁殖个数y(千个) 2.5 3 4 4.5
由最小二乘法得y与x的线性回归方程为=x+0.35,则样本在(4,3)处的残差为
( )
A.-0.15 B.0.15 C.-0.25 D.0.25
7.春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘” 总计
男 45 10 55
女 30 15 45
总计 75 25 100
附:
P(χ2≥xα) 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别无关”
C.有90%以上的把握认为“该市居民能否做到′光盘′与性别有关”
D.有90%以上的把握认为“该市居民能否做到′光盘′与性别无关”
8.2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有80%的男生喜欢网络课程,有40%的女生不喜欢网络课程,且有99%的把握但没有99.9%的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥xα) 0.1 0.05 0.01 0.001
xα 2.706 3.841 6.635 10.828
A.130 B.190 C.240 D.250
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.对于回归直线方程=x+,下列说法正确的是( )
A.直线必经过点(,)
B.x增加1个单位时,y平均增加个单位
C.样本数据中x=0时,可能有y=
D.样本数据中x=0时,一定有y=
10.根据下面的2×2列联表得到如下,4个判断正确的为( )
嗜酒 不嗜酒 总计
患肝病 700 60 760
未患肝病 200 32 232
总计 900 92 992
A.至少有99.9%的把握认为“患肝病与嗜酒有关”
B.至少有99%的把握认为“患肝病与嗜酒有关”
C.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关”
D.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒无关”
11.对两个变量x与y进行线性相关性和回归效果分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法正确的是( )
A.残差平方和越小的模型,拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心(,)
C.若变量x与y之间的相关系数r=0.80,则变量x与y之间具有很强的线性相关性
D.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
12.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在A地区的100天日落和夜晚天气,得到如下2×2列联表:
下雨 未下雨
出现 25 5
未出现 25 45
临界值表
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
并计算得到χ2≈19.05,下列小波对A地区天气判断正确的是( )
A.夜晚下雨的概率约为
B.未出现“日落云里走”夜晚下雨的概率约为
C.有99.9%的把握认为“′日落云里走′是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有99.9%的把握认为夜晚会下雨
三、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.如表提供的x和y是两组具有线性相关关系的数据,已知其回归方程为=0.65x+0.6,则m=________.?
x 3 5 7 9
y 2.5 4 m 6.5
14.某高校有10 000名学生,其中女生3 000名,男生7 000名.为调查爱好体育运动是否与性别有关,用分层抽样的方法抽取120名学生,制成独立性检验的2×2列表如表,则a-b=________.(用数字作答)?
男 女 合计
爱好体育运动 a 9 ####
不爱好体育运动 28 b ####
合计 #### #### 120
15.若对甲、乙、丙3组不同的数据作线性相关性检验,得到这3组数据的线性相关系数依次为0.93,0.42,-0.95,则线性相关程度最强的一组是________.(填甲、乙、丙中的一个)?
16.某产品在某零售摊位上的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如表所示:
x 16 17 18 19
y 50 44 41 31
由上表可得回归直线方程=x+中的=-6,则=__________,据此模型预计零售价定为15元时,每天的销售量为________.(第1空2分,第2空3分)?
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(10分)针对某新型病毒,某科研机构已研发出甲、乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占.
(1)根据题中数据,完成下面的列联表;
产生抗体 未产生抗体 合计
甲
乙
合计
(2)根据(1)中的列联表,判断能否有95%的把握认为甲、乙两种疫苗的效果有差异.
参考公式:χ2=,其中n=a+b+c+d.
参考数据:
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
18.(12分)在3+1+2的新高考模式下,某学校计划在高一下学期开设“物理”和“历史”两个选修科目.为了了解学生对这两个科目的选课意向,以便提前规划教育资源,教务处从高一年级500名学生(其中男生200人,女生300人)中,采用分层抽样的方法从中抽取部分学生进行调查.其中,女生比男生多抽取20人.
(1)请问总共抽取了多少名学生进行调查;
(2)新高考模式要求每名学生在“物理”和“历史”这两个科目中必须选择一个科目且只能选择一个科目,下表是根据调查结果得到的一个不完整的列联表,请将下面的列联表补充完整,并判断是否有99.9%的把握认为选择科目与性别有关?
选择“物理” 选择“历史” 总计
男生
女生 25
总计 55
附:χ2=,n=a+b+c+d.
P(χ2≥xα) 0.05 0.01 0.005 0.001
xα 3.841 6.635 7.879 10.828
19.(12分)为了了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如表:
患心肺疾病 不患心肺疾病 总计
大于40岁 16
小于等于40岁
12
总计
40
已知在40人中随机抽取1人,抽到不患心肺疾病的市民的概率为.
(1)请将2×2列联表补充完整;
(2)已知在大于40岁且患心肺疾病的市民中,有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出2人,记需住院治疗的人数为ξ,求ξ的分布列和数学期望;
(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
20.(12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得xi=60,yi=1 200,
(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
21.(12分)PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 周一 周二 周三 周四 周五
车流量x(万辆) 50 51 54 57 58
PM2.5的浓度y (微克/立方米) 69 70 74 78 79
(1)请根据表格数据,在如图所示的平面直角坐标系中画出散点图;
(2)根据表格数据,用最小二乘法求出y关于x的回归直线方程=x+;
(3)若周六同一时间的车流量是25万辆,试根据(2)中求出的回归直线方程预测此时PM2.5的浓度为多少(保留整数).
22.(12分)某城市9年前分别同时开始建设物流城和湿地公园,物流城3年建设完成,建成后若年投入x亿元,该年产生的经济净效益为(2ln x+5)亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为(x+3)亿元.
(1)对湿地公园,请在x=kn+b,x=kn2+b中选择一个合适模型,求投入额x与投入年份n的回归方程;
(2)从建设开始的第10年,若对物流城投入0.25亿元,预测这一年物流城和湿地公园哪个产生的年经济净效益高?请说明理由.
参考数据及公式:=0.336,nixi=6.22;当t=n2时,=11,=979,回归方程中的tixi=29.7;回归方程=s+斜率与截距=,=-s.
参考答案
一、选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列两个量之间的关系是相关关系的为( )
A.匀速直线运动的物体时间与位移的关系
B.学生的成绩和体重
C.路上酒后驾驶的人数和交通事故发生的多少
D.水的体积和重量
分析:选C.由匀速直线运动的物体时间与位移的关系公式知,是确定的函数关系,故A不对;学生的成绩和体重没有什么关系,故B不对;路上酒后驾驶的人数会影响交通事故发生的多少,但不是唯一因素,它们之间有相关性,故C对;水的体积V和重量x的关系为:V=k·x,是确定的函数关系,故D不对.
2.如图2×2列联表中a,b的值分别为( )
Y1 Y2 总计
X1 c a e
X2 23 d 48
总计 b 78 121
A.54,43 B.53,43
C.53,42 D.54,42
分析:选B.由2×2列联表可知,d=48-23=25,e=121-48=73,
所以a=78-d=78-25=53,c=e-a=73-53=20,
所以b=c+23=43.
3.根据如下样本数据:
x 3 4 5 6 7 8
y 4 2.5 -0.5 0.5 -2 -3
得到的回归直线方程为=x+,则( )
A.>0,<0 B.>0,>0
C.<0,>0 D.<0,<0
分析:选A.根据题意,画出散点图.
根据散点图,知两个变量为负相关,且回归直线与y轴的交点在y轴正半轴,
所以>0,<0.
4.设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的斜率是b,纵轴上的截距是a,那么必有( )
A.b与r的符号相同 B.a与r的符号相同
C.b与r的符号相反 D.a与r的符号相反
分析:选A.因为b>0时,两变量正相关,此时r>0;b<0时,两变量负相关,此时r<0.
5.对某同学7次考试的数学成绩x和物理成绩y进行分析,下面是该生7次考试的成绩.
数学 88 83 117 92 108 100 112
物理 94 91 108 96 104 101 106
发现他的物理成绩y与数学成绩x是线性相关的,利用最小二乘法得到线性回归方程为=0.5x+a,若该生的数学成绩达到130分,估计他的物理成绩大约是
( )
A.114.5 B.115 C.115.5 D.116
分析:选B.由题意可知
==100,
==100,
因为回归直线经过样本中心,
所以100=0.5×100+a,解得a=50,
线性回归方程为=0.5x+50,
该生的数学成绩达到130分,估计他的物理成绩大约是:0.5×130+50=115.
6.为研究某种细菌在特定环境下随时间变化的繁殖情况,得到如表实验数据:
天数x(天) 3 4 5 6
繁殖个数y(千个) 2.5 3 4 4.5
由最小二乘法得y与x的线性回归方程为=x+0.35,则样本在(4,3)处的残差为
( )
A.-0.15 B.0.15 C.-0.25 D.0.25
分析:选A.因为=×(3+4+5+6)=4.5,
=(2.5+3+4+4.5)=3.5,
因为回归直线经过样本中心,所以3.5=4.5+0.35,
解得=0.7,
线性回归方程为=0.7x+0.35,
x=4时,=0.7×4+0.35=3.15.
所以样本在(4,3)处的残差为:3-3.15=-0.15.
7.春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到“光盘” 能做到“光盘” 总计
男 45 10 55
女 30 15 45
总计 75 25 100
附:
P(χ2≥xα) 0.10 0.05 0.025
xα 2.706 3.841 5.024
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别有关”
B.在犯错误的概率不超过1%的前提下,认为“该市居民能否做到′光盘′与性别无关”
C.有90%以上的把握认为“该市居民能否做到′光盘′与性别有关”
D.有90%以上的把握认为“该市居民能否做到′光盘′与性别无关”
分析:选C.由公式可计算
χ2=≈3.03>2.706,
所以有90%以上的把握认为“该市居民能否做到′光盘′与性别有关”.
8.2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播、微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男、女学生,发现有80%的男生喜欢网络课程,有40%的女生不喜欢网络课程,且有99%的把握但没有99.9%的把握认为是否喜欢网络课程与性别有关,则被调查的男、女学生总数量可能为( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥xα) 0.1 0.05 0.01 0.001
xα 2.706 3.841 6.635 10.828
A.130 B.190 C.240 D.250
分析:选B.依题意,设男、女生的人数各为5x,建立2×2列联表如表所示:
喜欢网络课程 不喜欢网络课程 总计
男生 4x x 5x
女生 3x 2x 5x
总计 7x 3x 10x
故χ2==,由题可知6.635<<10.828,
所以139.335<10x<227.388.只有B符合题意.
二、多项选择题(本大题共4小题,每小题5分,共20分,全部选对得5分,选对但不全的得3分,有选错的得0分)
9.对于回归直线方程=x+,下列说法正确的是( )
A.直线必经过点(,)
B.x增加1个单位时,y平均增加个单位
C.样本数据中x=0时,可能有y=
D.样本数据中x=0时,一定有y=
分析:选ABC.回归直线方程是根据样本数据得到的一个近似曲线,故由它得到的值也是一个近似值,D选项错误,其他选项均正确.
10.根据下面的2×2列联表得到如下,4个判断正确的为( )
嗜酒 不嗜酒 总计
患肝病 700 60 760
未患肝病 200 32 232
总计 900 92 992
A.至少有99.9%的把握认为“患肝病与嗜酒有关”
B.至少有99%的把握认为“患肝病与嗜酒有关”
C.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关”
D.在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒无关”
分析:选BC.由2×2列联表中数据可求得χ2=≈7.349>6.635,
所以在犯错误的概率不超过0.01的前提下,认为“患肝病与嗜酒有关”,
即至少有99%的把握认为“患肝病与嗜酒有关”.因此BC正确.
11.对两个变量x与y进行线性相关性和回归效果分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法正确的是( )
A.残差平方和越小的模型,拟合的效果越好
B.由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心(,)
C.若变量x与y之间的相关系数r=0.80,则变量x与y之间具有很强的线性相关性
D.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
分析:选ABC.对两个变量x与y进行线性相关性和回归效果分析,得到一组样本数据.残差平方和越小的模型,拟合的效果越好,故A正确;由样本数据利用最小二乘法得到的回归方程表示的直线必过样本点的中心(,),故B正确;若变量x与y之间的相关系数r=0.80>0.75,则变量x与y之间具有很强的线性相关性,故C正确;用相关指数R2来刻画回归效果,R2越大,说明模型的拟合效果越好,故D错误.
12.千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在A地区的100天日落和夜晚天气,得到如下2×2列联表:
下雨 未下雨
出现 25 5
未出现 25 45
临界值表
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
并计算得到χ2≈19.05,下列小波对A地区天气判断正确的是( )
A.夜晚下雨的概率约为
B.未出现“日落云里走”夜晚下雨的概率约为
C.有99.9%的把握认为“′日落云里走′是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有99.9%的把握认为夜晚会下雨
分析:选ABC.对于选项A:因为夜晚下雨的天数一共有25+25=50(天),所以夜晚下雨的概率约为=,故A正确;对于选项B:未出现“日落云里走”夜晚下雨的有25天,未出现“日落云里走”的一共25+45=70(天),所以未出现“日落云里走”夜晚下雨的概率约为=,故B正确;
对于选项C:因为χ2≈19.05>10.828,所以有99.9%的把握认为“‘日落云里走’′是否出现”与“当晚是否下雨”有关,故C正确,D错误.
三、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.如表提供的x和y是两组具有线性相关关系的数据,已知其回归方程为=0.65x+0.6,则m=________.?
x 3 5 7 9
y 2.5 4 m 6.5
分析:==6,==,
所以样本点的中心为,
代入=0.65x+0.6,得=0.65×6+0.6,
解得m=5.
答案:5
14.某高校有10 000名学生,其中女生3 000名,男生7 000名.为调查爱好体育运动是否与性别有关,用分层抽样的方法抽取120名学生,制成独立性检验的2×2列表如表,则a-b=________.(用数字作答)?
男 女 合计
爱好体育运动 a 9 ####
不爱好体育运动 28 b ####
合计 #### #### 120
分析:根据分层抽样原理,计算抽取男生120×=84(人),
女生120×=36(人),
所以a=84-28=56(人),b=36-9=27(人),
所以a-b=56-27=29(人).
答案:29
15.若对甲、乙、丙3组不同的数据作线性相关性检验,得到这3组数据的线性相关系数依次为0.93,0.42,-0.95,则线性相关程度最强的一组是________.(填甲、乙、丙中的一个)?
分析:两个变量y与x的回归模型中,它们的相关系数|r|越接近于1,这个模型的两个变量线性相关程度就越强,在甲、乙、丙中,所给的数值中-0.95的绝对值最接近1,所以丙的线性相关程度最强.
答案:丙
16.某产品在某零售摊位上的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如表所示:
x 16 17 18 19
y 50 44 41 31
由上表可得回归直线方程=x+中的=-6,则=__________,据此模型预计零售价定为15元时,每天的销售量为________.(第1空2分,第2空3分)?
分析:由题意知=17.5,=41.5,代入回归直线方程得=146.5,所以回归直线方程为=-6x+146.5,当x=15时,=146.5-15×6=56.5.
答案:146.5 56.5
四、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(10分)针对某新型病毒,某科研机构已研发出甲、乙两种疫苗,为比较两种疫苗的效果,选取100名志愿者,将他们随机分成两组,每组50人.第一组志愿者注射甲种疫苗,第二组志愿者注射乙种疫苗,经过一段时间后,对这100名志愿者进行该新型病毒抗体检测,发现有的志愿者未产生该新型病毒抗体,在未产生该新型病毒抗体的志愿者中,注射甲种疫苗的志愿者占.
(1)根据题中数据,完成下面的列联表;
产生抗体 未产生抗体 合计
甲
乙
合计
(2)根据(1)中的列联表,判断能否有95%的把握认为甲、乙两种疫苗的效果有差异.
参考公式:χ2=,其中n=a+b+c+d.
参考数据:
P(χ2≥xα) 0.10 0.05 0.010 0.001
xα 2.706 3.841 6.635 10.828
分析:(1)由题意可得未产生该新型病毒抗体的志愿者的人数为100×=10,
则注射甲种疫苗的志愿者中未产生抗体的人数为10×=2,产生抗体的人数为50-2=48;
注射乙种疫苗的志愿者中未产生抗体的人数为10-2=8,产生抗体的人数为50-8=42.
产生抗体 未产生抗体 合计
甲 48 2 50
乙 42 8 50
合计 90 10 100
(2)计算χ2===4,
因为4>3.841,所以有95%的把握认为甲、乙两种疫苗的效果有差异.
18.(12分)在3+1+2的新高考模式下,某学校计划在高一下学期开设“物理”和“历史”两个选修科目.为了了解学生对这两个科目的选课意向,以便提前规划教育资源,教务处从高一年级500名学生(其中男生200人,女生300人)中,采用分层抽样的方法从中抽取部分学生进行调查.其中,女生比男生多抽取20人.
(1)请问总共抽取了多少名学生进行调查;
(2)新高考模式要求每名学生在“物理”和“历史”这两个科目中必须选择一个科目且只能选择一个科目,下表是根据调查结果得到的一个不完整的列联表,请将下面的列联表补充完整,并判断是否有99.9%的把握认为选择科目与性别有关?
选择“物理” 选择“历史” 总计
男生
女生 25
总计 55
附:χ2=,n=a+b+c+d.
P(χ2≥xα) 0.05 0.01 0.005 0.001
xα 3.841 6.635 7.879 10.828
分析:(1)设女生抽取x人,则男生抽取(x-20)人,
则x∶(x-20)=3∶2,解得x=60,
所以总共抽取了60+(60-20)=100(人).
(2)根据题意补充完整列联表如表.
选择“物理” 选择“历史” 总计
男生 30 10 40
女生 25 35 60
总计 55 45 100
由表中数据,
计算χ2==≈10.774<10.828,
所以没有99.9%的把握认为选择科目与性别有关.
19.(12分)为了了解心肺疾病是否与年龄相关,现随机抽取了40名市民,得到数据如表:
患心肺疾病 不患心肺疾病 总计
大于40岁 16
小于等于40岁
12
总计
40
已知在40人中随机抽取1人,抽到不患心肺疾病的市民的概率为.
(1)请将2×2列联表补充完整;
(2)已知在大于40岁且患心肺疾病的市民中,有4名重症患者,专家建议重症患者住院治疗,现从这16名患者中选出2人,记需住院治疗的人数为ξ,求ξ的分布列和数学期望;
(3)能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关?
分析:(1)将2×2列联表补充完整:
患心肺疾病 不患心肺疾病 总计
大于40岁 16 4 20
小于等于40岁 8 12 20
总计 24 16 40
(2)ξ的可能取值为0,1,2.
P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,
所以随机变量ξ的分布列为
ξ 0 1 2
P
故ξ的数学期望E(ξ)=0×+1×+2×=.
(3)χ2==>6.635,
所以能在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关.
20.(12分)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中xi和yi分别表示第i个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得xi=60,yi=1 200,
(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800.
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数r=,≈1.414.
分析:(1)由已知,yi=1 200,
所以20个样区野生动物数量的平均数为yi=1 200=60,
所以该地区这种野生动物数量的估计值为60×200=12 000;
(2)因为(xi-)2=80,(yi-)2=9 000,(xi-)(yi-)=800,
所以r====≈0.94;
(3)更合理的抽样方法是分层抽样,根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.
理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.
21.(12分)PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 周一 周二 周三 周四 周五
车流量x(万辆) 50 51 54 57 58
PM2.5的浓度y (微克/立方米) 69 70 74 78 79
(1)请根据表格数据,在如图所示的平面直角坐标系中画出散点图;
(2)根据表格数据,用最小二乘法求出y关于x的回归直线方程=x+;
(3)若周六同一时间的车流量是25万辆,试根据(2)中求出的回归直线方程预测此时PM2.5的浓度为多少(保留整数).
分析:(1)散点图如图.
(2)因为==54,
==74.
(xi-)(yi-)=4×5+3×4+3×4+4×5=64,
(xi-)2=(-4)2+(-3)2+32+42=50,
所以===1.28,
=-=74-1.28×54=4.88,
故y关于x的回归直线方程为=1.28x+4.88.
(3)当x=25时,y=1.28×25+4.88=36.88≈37,
所以可以预测此时PM2.5的浓度约为37微克/立方米.
22.(12分)某城市9年前分别同时开始建设物流城和湿地公园,物流城3年建设完成,建成后若年投入x亿元,该年产生的经济净效益为(2ln x+5)亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为(x+3)亿元.
(1)对湿地公园,请在x=kn+b,x=kn2+b中选择一个合适模型,求投入额x与投入年份n的回归方程;
(2)从建设开始的第10年,若对物流城投入0.25亿元,预测这一年物流城和湿地公园哪个产生的年经济净效益高?请说明理由.
参考数据及公式:=0.336,nixi=6.22;当t=n2时,=11,=979,回归方程中的tixi=29.7;回归方程=s+斜率与截距=,=-s.
分析:(1)根据散点图,应该选择模型x=kn2+b.
令t=n2,
则===0.03,
所以=-=0.336-0.03×11=0.006,
所以所求回归方程是=0.03t+0.006,即=0.03n2+0.006.
(2)若年投入x亿元,该年产生的经济净效益为(2ln x+5)亿元;即物流城第10年的年经济净效益为2ln 0.25+5=5-4ln 2亿元;根据回归方程可估计湿地公园第10年的投入约为0.03×62+0.006=1.086
亿元,该年的经济效益为1.086+3=4.086亿元.
因为4.086>5-4ln 2,
所以该年湿地公园产生的年经济净效益高.
