1.4二次函数与一元二次方程的联系 同步练习(含解析)
文档属性
| 名称 | 1.4二次函数与一元二次方程的联系 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 06:56:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学湘教版九年级下册1.4二次函数与一元二次方程的联系 同步练习
一、单选题
1. 抛物线 与y轴交点的坐标是(??? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
2.二次函数 的顶点坐标为 ,其部分图象如图所示.以下结论错误的是(?? )
A.?????????
B.?????????
C.?????????
D.?关于x的方程 无实数根
3.根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0)的一个根x的大致范围是(??? )
x 6.17 6.18 6.19 6.20
ax2+bx+c ?0.03 ?0.01 0.02 0.04
A.?6.194.若二次函数 的图象与 轴有两个交点,则关于 的一元二次方程 的根的情况是(? )
A.?有两个不相等的实数根?????????????
B.?有两个相等的实数根?????????????
C.?没有实数根?????????????
D.?不能确定
5.已知抛物线y=- x2+ x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( ??)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
6.已知抛物线 与x轴的两个交点坐标是(-2,0),(5,0),则一元二次方程 的两个解是(??? )
A.???????????B.??????????????C.??????????????D.?
7.已知二次函数y=x2-2ax+a2-2a-4(a为常数)的图象与x轴有交点,则a的取值范围是(?????? )
A.?a>-2????????????????????????????????B.?a≥-2????????????????????????????????C.?a<-2????????????????????????????????D.?a≤-2
8.若函数y=(m﹣1)x2﹣6x+ m的图象与x轴有且只有一个交点,则m的值为( )
A.?﹣2或3?????????????????????????B.?﹣2或﹣3?????????????????????????C.?1或﹣2或3?????????????????????????D.?1或﹣2或﹣3
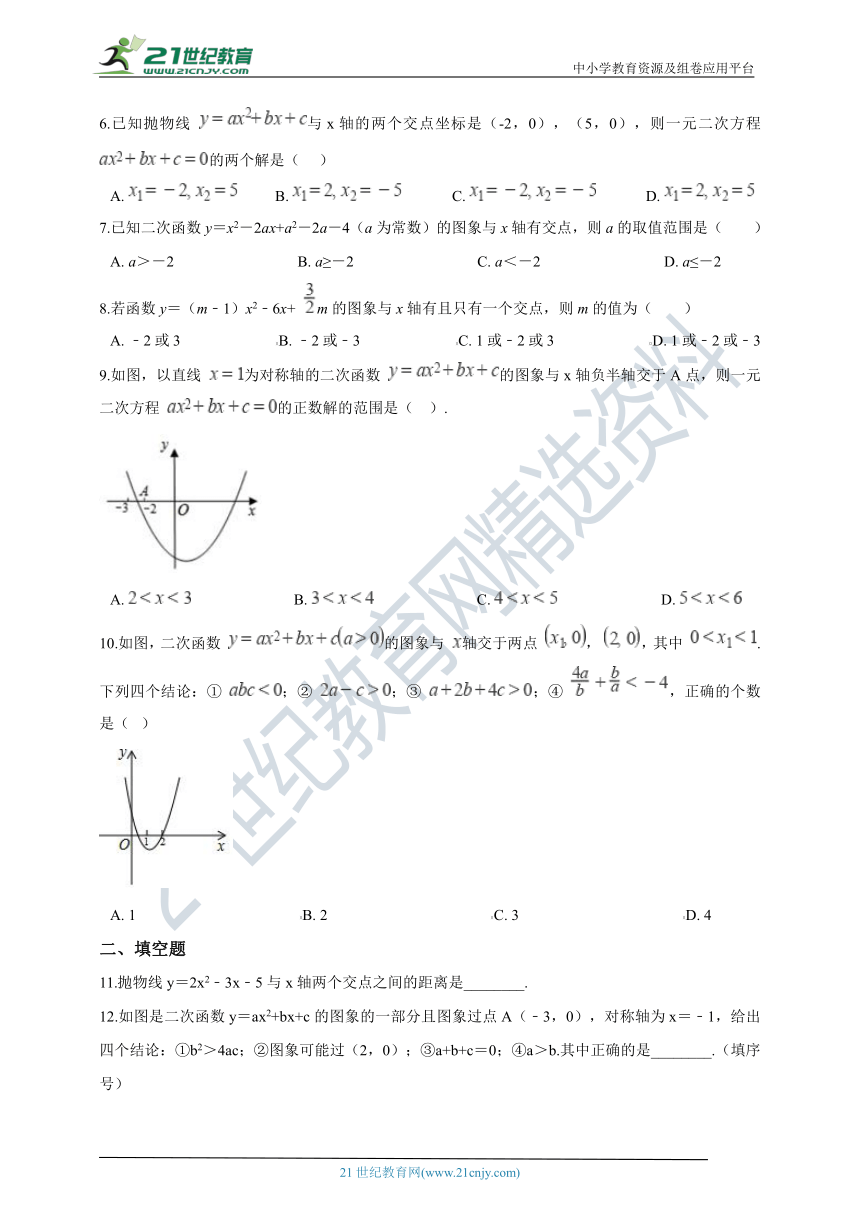
9.如图,以直线 为对称轴的二次函数 的图象与x轴负半轴交于A点,则一元二次方程 的正数解的范围是(?? ).
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
10.如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是(? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
11.抛物线y=2x2﹣3x﹣5与x轴两个交点之间的距离是________.
12.如图是二次函数y=ax2+bx+c的图象的一部分且图象过点A(﹣3,0),对称轴为x=﹣1,给出四个结论:①b2>4ac;②图象可能过(2,0);③a+b+c=0;④a>b.其中正确的是________.(填序号)
13.若函数 的图象与x轴没有交点,则m的取值范围是________.
14.在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:
… 1 2 3 4 5 6 7 8 …
… -1.78 -3.70 -4.42 -3.91 -2.20
4.88 10.27 …
根据以上信息,关于 的一元二次方程 的两个实数根中,其中的一个实数根约等于________(结果保留小数点后一位).
15.二次函数 与x轴的两个交点的横坐标分别为m和n , 且 ,则a , b , m , n四个数的大小关系是________(用<号连接)
三、解答题
16.已知抛物线的解析式为 ,求证:无论m取何值,抛物线与x轴总有两个交点.
17.已知关于x的二次函数 .
(1)试判断该函数的图象与x轴的交点的个数;
(2)当 时,求该函数图象与x轴的两个交点之间的距离.
18.如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)
(1)写出抛物线的解析式、开口方向、对称轴;
(2)求出图象与x轴的交点A、B的坐标;
(3)在二次函数的图象上是否存在点P , 使S△PAB=S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
19.某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
20.我们可以通过下列步骤估计方程x2﹣2x﹣2=0方程的根所在的范围.
第一步:画出函数y=x2﹣2x﹣2=0的图象,发现函数图象是一条连续不断的曲线,且与x轴的一个交点的横坐标在0,﹣1之间.
第二步:因为当x=0时,y=﹣2<0,当x=﹣1时,y=1>0,
所以可确定方程x2﹣2x﹣2=0的一个根x1所在的范围是﹣1<x1<0
第三步:通过取0和﹣1的平均数缩小x1所在的范围:
取x= ,因为当x= 对,y<0.又因为当x=﹣1时,y>0,所以
(1)请仿照第二步,通过运算验证方程x2﹣2x﹣2=0的另一个根x2所在的范围是2<x2<3
(2)在2<x2<3的基础上,重复应用第三步中取平均数的方法,将x2所在的范围缩小至a<x2<b , 使得 .
答案解析部分
一、单选题
1. B
考点:二次函数图象与坐标轴的交点问题
解:令 ,得 ,故抛物线与y轴交点坐标为 .
故答案为:B.
分析:此题令 ,可确定抛物线与y轴的交点坐标.
2. C
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征
解: 抛物线开口向下,
,
对称轴为直线 ,
,
抛物线与y轴交于正半轴,
,
,
故A正确;
B. 抛物线与x轴有两个交点,
,即 ,
故B正确;
C. 抛物线的对称轴为直线 ,抛物线与x轴的一个交点在 和 之间,
抛物线与x轴的另一个交点在 和 之间,
时, ,
即 ,
,
,
故C错误;
D. 抛物线开口向下,顶点为 ,
函数有最大值n,
抛物线 与直线 无交点,
一元二次方程 无实数根,
故D正确.
故答案为:C
分析:根据抛物线开口方向,对称轴的位置以及与y轴的交点可以对A进行判断;根据抛物线与x轴的交点情况可对B进行判断; 时, ,可对C进行判断;根据抛物线 与直线 无交点,可对D进行判断.
3. B
考点:利用二次函数图象求一元二次方程的近似根
解:∵当x=6.18时,y=?0.01<0;当x=6.19时,y=0.02>0,
∴当x在6.18<x<6.19的范围内取某一值时,对应的函数值为0,即ax2+bx+c=0,
∴方程ax2+bx+c=0(其中a,b,c是常数,且a≠0)的一个根x的大致范围为6.18<x<6.19.
故答案为:B.
分析:观察表中数据得到当x=6.18时,y=?0.01<0;当x=6.19时,y=0.02>0,则可判断当x在6.18<x<6.19的范围内取某一值时,对应的函数值为0,即ax2+bx+c=0,所以可确定方程ax2+bx+c=0的一个根的大致范围为6.18<x<6.19.
4. A
考点:一元二次方程根的判别式及应用,二次函数图象与坐标轴的交点问题
解:∵二次函数y=3x2+2x-2m的图象与x轴有两个交点,
∴当y=0时,3x2+2x-2m=0,
此时使得3x2+2x-2m=0成立的x的值有两个,
∴关于x的一元二次方程3x2+2x=2m的根的情况是有两个不相等的实数根,
故答案为:A.
分析:根据二次函数y=3x2+2x-2m的图象与x轴有两个交点,进行判断作答即可。
5. D
考点:二次函数图象与坐标轴的交点问题,勾股定理
解:把y=0代入
得 ,
解得 ,
∴A(-3,0),B(9,0),即可得AB=15,
∵又因D为AB的中点,
可得AD=BD=7.5,
求得OD=4.5,
在Rt△COD中,由勾股定理可得CD=7.5,故答案选D.
分析:令y=0,即可得到A和B的坐标,根据D为AB的中点,即可得到OD的长度,根据勾股定理求出CD即可。
6. A
考点:利用二次函数图象判断一元二次方程根的情况
解:∵抛物线 与 轴的交点的横坐标就是方程 的根,
∴ ( )的解是 .
故答案为:A.
分析:根据抛物线 与x轴的交点得横坐标就是方程 的根来解决此题.
7. B
考点:二次函数图象与坐标轴的交点问题
解:根据题意可得: ,
解得: .
故答案为:B.
分析:将二次函数图像与x轴的交点个数问题转化为一元二次方程根的判别式求解即可。
8. C
考点:二次函数图象与坐标轴的交点问题
解:当m=1时,函数解析式为:y=﹣6x+ 是一次函数,图象与x轴有且只有一个交点,
当m≠1时,函数为二次函数,
∵函数y=(m﹣1)x2﹣6x+ m的图象与x轴有且只有一个交点,
∴62﹣4×(m﹣1)× m=0,
解得,m=﹣2或3,
故答案为:C .
分析:本题需分类讨论,当m=1时,有且只有一个交点;当m≠1时,利用一元二次方程根的判别式求解即可。
9. C
考点:利用二次函数图象求一元二次方程的近似根
解:∵二次函数 的对称轴为 ,
而对称轴左侧图象与x轴交点横坐标的取值范围是 ,
∴右侧交点横坐标的取值范围是 .
故答案为:C.
分析:先根据图象得出对称轴左侧图象与x轴交点横坐标的取值范围,再利用对称轴 ,可以算出右侧交点横坐标的取值范围.
10. C
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征
解:①∵抛物线开口向上,∴ ,
∵抛物线对称轴在 轴的右侧,∴a,b异号,∴ ,
∵抛物线与 轴的交点在 轴上方,∴ ,
∴ ,所以①正确;
②∵图象与 轴交于两点 , ,其中 ,
∴ ,∴ ,
当 时, ,
∵当 时, ,
∴ ,∴ ,∴ ,故②正确;
③当 时, 值为 ,给 乘以4,即可化为 ,
∵当 时,由图象可知在 和x1之间 为正值,
当 时,在 和x1之间 为负值,
∴ 与0的关系不能确定,故③错误;
④∵ ,∴ ,∴ ,
即 ,∴ ,
∵ , ,∴ ,
∴ ,即 .
所以④正确.
综上,正确的是①②④,共3个,
故答案为:C.
分析:由于抛物线开口向上,可得,由抛物线对称轴在 轴的右侧,可得?,由抛物线与 轴的交点在 轴上方,可得, 据此判断①;由于图象与 轴交于两点 , ,其中 ?,从而可得, 当 时,, 求出, 从而可得,据此求出, 据此判断②;当 时, 值为 ,给 乘以4,即可化为 , 由于, 无法确定当时,所对抛物线上的点在x轴上方还是下方,据此判断③;由, 可得, 即得?,从而得出?,由于, 可得, 据此即可判断④.
二、填空题
11.
考点:二次函数图象与坐标轴的交点问题
解:当y=0时,2x2﹣3x﹣5=0,
解得,x1= ,x2=﹣1,
∵ ﹣(﹣1)= ,
∴抛物线y=2x2﹣3x﹣5与x轴两个交点之间的距离是 ,
故答案为: .
分析:由题意令y=0可得关于x的一元二次方程,解这个方程可求得抛物线与x轴的两个交点的横坐标,再根据数轴上两个点之间的距离等于两点坐标之差的绝对值可求解.
12. ①③④
考点:二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的图象
解:①∵二次函数的图象与x轴有两个交点,
∴b2﹣4ac>0,
即b2>4ac,故①正确;②∵抛物线的一个交点为(﹣3,0))对称轴为x=﹣1,
∴另一个交点为(1,0),
∴图象过点(1,0),不会经过(2,0),故②错误错误;③∵抛物线经过点(1,0),
∴y=a+b+c=0,故③正确;④∵抛物线开口向下,
∴a<0,
∵﹣ =﹣1,
∴b=2a,
∴a﹣b=a﹣2a=﹣a>0,故④正确;
故正确的为①③④,
故答案为①③④.
分析:①观察图像可知,二次函数的图象与x轴有两个交点,于是根据二次函数与一元二次方程的关系可得,b2﹣4ac>0,移项可得b2>4ac;
②由抛物线是轴对称图形可知,抛物线的对称轴与x轴的交点是抛物线与x轴的两个交点的中点,由线段中点得意义可求出抛物线与x轴的另一个交点坐标,结合选项可判断求解;
③由②的计算可知抛物线与x轴的另一个交点坐标为(1,0),把x=1代入解析式计算可求解;
④由图知,抛物线的对称轴是x=-1=-, 整理可求解.
13. m>1
考点:二次函数图象与坐标轴的交点问题
解:∵二次函数y=x2-2x+m的图象与x轴没有交点,
∴方程x2-2x+m=0没有实数根,
∴判别式△=(-2)2-4×1×m<0,
解得:m>1;
故答案为:m>1.
分析:将二次函数图像与x轴交点个数的问题转化为求一元二次方程根的个数的问题,即求根的判别式即可。
14. 5.8
考点:利用二次函数图象求一元二次方程的近似根
解:由表格可知,
当x=5时,y=-2.20<0,当x=6时,y=0.75>0,
则关于x的一元二次方程 的两个实数根中,其中的一个实数根约等于5.8(5.6至5.9均可),
故答案为:5.8.
分析:根据二次函数与一元二次方程近似根的关系,先找y的值,再判断即可。
15. m考点:二次函数与不等式(组)的综合应用
解:二次函数 与 轴交点的横坐标为 、 ,将其图象往下平移2个单位长度可得出二次函数 的图象,如图所示:
观察图象,可知:m故答案为:m
分析:画出函数的草图,结合草图求解即可。
三、解答题
16. 解:令y=0,
∴ >0
∴无论m取何值,抛物线与x轴总有两个交点
考点:二次函数图象与坐标轴的交点问题
分析:将二次函数与x轴的交点问题转化为一元二次方程根的判别式求解即可。
17. (1)解: ,
, ,
二次函数 的图象与x轴有两个交点;
(2)解:当 时,二次函数为 ,令 ,
则 ,
解得 或 , 与x轴交点为 , ,
两交点间的距离为:
考点:二次函数图象与坐标轴的交点问题
分析:(1)利用根的判别式判断二次函数与x轴的交点坐标即可求解;
(2)先求出二次函数与x轴的交点坐标,再求两点之间的距离即可。
18. (1)∵抛物线解析式为y=(x+m)2+k的顶点为M(1,-4)
∴y=(x-1)2-4,抛物线对称轴是直线x=1.
∵a=1>0,
∴抛物线开口方向向上
(2)∵抛物线解析式为y=(x-1)2-4,
令y=0,得(x-1)2-4=0,
解得x1=3,x2=-1,
∴A(-1,0),B(3,0)
(3)∵△PAB与△MAB同底,且S△PAB=S△MAB ,
∴ =4,即yP=±4,
又∵点P在y=(x-1)2-4的图象上,yP≥-4,
∴yP=4,则(x-1)2-4=4,
解得x1= ,x2= ,
∴存在合适的点P,坐标为( ,4)或( ,4).
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征
分析:(1)根据抛物线的顶点坐标可以得到抛物线解析式,结合解析式写出抛物线的开口方向和对称轴;(2)由条件可先求得二次函数的解析式,再令y=0可求得A、B两点的坐标;(3)由条件可先求得P点的纵坐标,再代入解析式可求得P点坐标.
19. (1)解:设增加x棵桔子树.
由题意得
解之得x1=10,x2=130
∵成本最少,∴x=10
答:增加10棵桔子树时收益可以达到6650kg.
(2)设总的收益为W
则W= = =
∵10≤x≤40
∴当x=10时,Wmin=6650
当x=40时,Wmax=8000
答:果园最少产6650kg,最多产8000kg。
考点:二次函数图象与一元二次方程的综合应用,二次函数的其他应用
分析:(1)利用增加桔子树后:树的棵树×每一棵树的产量=6650,列方程即可求解。
(2)根据题意列出W与x的函数解析式,再将函数解析式转化为顶点式,然后利用二次函数的性质求解。
20. (1)解:因为当x=2时,y=﹣2<0,当x=3时,y=1>0,
所以可确定方程x2﹣2x﹣2=0的一个根x2所在的范围是2<x2<3;
(2)解:取x= =2.5,因为当x=2.5时,y<0.
又因为当x=3时,y>0,所以2.5<x2<3,
取x= =2.75,因为当x=2.75时,y>0.
又因为当x=2.5时,y<0,所以2.5<x2<2.75,
因为2.75﹣2.5= .
取x= =2.625,因为当x=2.625时,y<0.
又因为当x=2.75时,y>0,所以2.625<x2<2.75,
因为2,75﹣2,625= < ,
所以2.625<x2<2.75即为所求x2 的范围
考点:利用二次函数图象求一元二次方程的近似根
分析:(1)确定当x=2或 x=3时y的正负由此即可验证;(2)取第三步2和3的平均数x=2.5,计算y的值可得2.5<x2<3,再进一步取2.5和3的平均数x=2.75,计算y的值可得2.5<x2<2.75,再一次取平均数直到 即可
_21?????????è?????(www.21cnjy.com)_
初中数学湘教版九年级下册1.4二次函数与一元二次方程的联系 同步练习
一、单选题
1. 抛物线 与y轴交点的坐标是(??? )
A.?????????????????????????????????B.?????????????????????????????????C.?????????????????????????????????D.?
2.二次函数 的顶点坐标为 ,其部分图象如图所示.以下结论错误的是(?? )
A.?????????
B.?????????
C.?????????
D.?关于x的方程 无实数根
3.根据下列表格的对应值:判断方程ax2+bx+c=0(a≠0)的一个根x的大致范围是(??? )
x 6.17 6.18 6.19 6.20
ax2+bx+c ?0.03 ?0.01 0.02 0.04
A.?6.19
A.?有两个不相等的实数根?????????????
B.?有两个相等的实数根?????????????
C.?没有实数根?????????????
D.?不能确定
5.已知抛物线y=- x2+ x+6与x轴交于点A,点B,与y轴交于点C.若D为AB的中点,则CD的长为( ??)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
6.已知抛物线 与x轴的两个交点坐标是(-2,0),(5,0),则一元二次方程 的两个解是(??? )
A.???????????B.??????????????C.??????????????D.?
7.已知二次函数y=x2-2ax+a2-2a-4(a为常数)的图象与x轴有交点,则a的取值范围是(?????? )
A.?a>-2????????????????????????????????B.?a≥-2????????????????????????????????C.?a<-2????????????????????????????????D.?a≤-2
8.若函数y=(m﹣1)x2﹣6x+ m的图象与x轴有且只有一个交点,则m的值为( )
A.?﹣2或3?????????????????????????B.?﹣2或﹣3?????????????????????????C.?1或﹣2或3?????????????????????????D.?1或﹣2或﹣3
9.如图,以直线 为对称轴的二次函数 的图象与x轴负半轴交于A点,则一元二次方程 的正数解的范围是(?? ).
A.????????????????????????????B.????????????????????????????C.????????????????????????????D.?
10.如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是(? )
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
11.抛物线y=2x2﹣3x﹣5与x轴两个交点之间的距离是________.
12.如图是二次函数y=ax2+bx+c的图象的一部分且图象过点A(﹣3,0),对称轴为x=﹣1,给出四个结论:①b2>4ac;②图象可能过(2,0);③a+b+c=0;④a>b.其中正确的是________.(填序号)
13.若函数 的图象与x轴没有交点,则m的取值范围是________.
14.在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:
… 1 2 3 4 5 6 7 8 …
… -1.78 -3.70 -4.42 -3.91 -2.20
4.88 10.27 …
根据以上信息,关于 的一元二次方程 的两个实数根中,其中的一个实数根约等于________(结果保留小数点后一位).
15.二次函数 与x轴的两个交点的横坐标分别为m和n , 且 ,则a , b , m , n四个数的大小关系是________(用<号连接)
三、解答题
16.已知抛物线的解析式为 ,求证:无论m取何值,抛物线与x轴总有两个交点.
17.已知关于x的二次函数 .
(1)试判断该函数的图象与x轴的交点的个数;
(2)当 时,求该函数图象与x轴的两个交点之间的距离.
18.如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)
(1)写出抛物线的解析式、开口方向、对称轴;
(2)求出图象与x轴的交点A、B的坐标;
(3)在二次函数的图象上是否存在点P , 使S△PAB=S△MAB?若存在,求出点P的坐标;若不存在,请说明理由.
19.某果农在其承包的果园中种植了60棵桔子树,每棵桔子树的产量是100kg,果农想增加桔子树的棵数来增产,但增加果树会导致每棵树的光照减少,使得单棵果树产量减少,试验发现每增加1棵桔子树,单棵桔子树的产量减少0.5kg.
(1)在投入成本最低的情况下,增加多少棵桔子树时,可以使果园总产量达到6650kg?
(2)设增加x棵桔子树,考虑实际增加桔子树的情况,10≤x≤40,请你计算一下,果园总产量最多为多少kg,最少为多少kg?
20.我们可以通过下列步骤估计方程x2﹣2x﹣2=0方程的根所在的范围.
第一步:画出函数y=x2﹣2x﹣2=0的图象,发现函数图象是一条连续不断的曲线,且与x轴的一个交点的横坐标在0,﹣1之间.
第二步:因为当x=0时,y=﹣2<0,当x=﹣1时,y=1>0,
所以可确定方程x2﹣2x﹣2=0的一个根x1所在的范围是﹣1<x1<0
第三步:通过取0和﹣1的平均数缩小x1所在的范围:
取x= ,因为当x= 对,y<0.又因为当x=﹣1时,y>0,所以
(1)请仿照第二步,通过运算验证方程x2﹣2x﹣2=0的另一个根x2所在的范围是2<x2<3
(2)在2<x2<3的基础上,重复应用第三步中取平均数的方法,将x2所在的范围缩小至a<x2<b , 使得 .
答案解析部分
一、单选题
1. B
考点:二次函数图象与坐标轴的交点问题
解:令 ,得 ,故抛物线与y轴交点坐标为 .
故答案为:B.
分析:此题令 ,可确定抛物线与y轴的交点坐标.
2. C
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征
解: 抛物线开口向下,
,
对称轴为直线 ,
,
抛物线与y轴交于正半轴,
,
,
故A正确;
B. 抛物线与x轴有两个交点,
,即 ,
故B正确;
C. 抛物线的对称轴为直线 ,抛物线与x轴的一个交点在 和 之间,
抛物线与x轴的另一个交点在 和 之间,
时, ,
即 ,
,
,
故C错误;
D. 抛物线开口向下,顶点为 ,
函数有最大值n,
抛物线 与直线 无交点,
一元二次方程 无实数根,
故D正确.
故答案为:C
分析:根据抛物线开口方向,对称轴的位置以及与y轴的交点可以对A进行判断;根据抛物线与x轴的交点情况可对B进行判断; 时, ,可对C进行判断;根据抛物线 与直线 无交点,可对D进行判断.
3. B
考点:利用二次函数图象求一元二次方程的近似根
解:∵当x=6.18时,y=?0.01<0;当x=6.19时,y=0.02>0,
∴当x在6.18<x<6.19的范围内取某一值时,对应的函数值为0,即ax2+bx+c=0,
∴方程ax2+bx+c=0(其中a,b,c是常数,且a≠0)的一个根x的大致范围为6.18<x<6.19.
故答案为:B.
分析:观察表中数据得到当x=6.18时,y=?0.01<0;当x=6.19时,y=0.02>0,则可判断当x在6.18<x<6.19的范围内取某一值时,对应的函数值为0,即ax2+bx+c=0,所以可确定方程ax2+bx+c=0的一个根的大致范围为6.18<x<6.19.
4. A
考点:一元二次方程根的判别式及应用,二次函数图象与坐标轴的交点问题
解:∵二次函数y=3x2+2x-2m的图象与x轴有两个交点,
∴当y=0时,3x2+2x-2m=0,
此时使得3x2+2x-2m=0成立的x的值有两个,
∴关于x的一元二次方程3x2+2x=2m的根的情况是有两个不相等的实数根,
故答案为:A.
分析:根据二次函数y=3x2+2x-2m的图象与x轴有两个交点,进行判断作答即可。
5. D
考点:二次函数图象与坐标轴的交点问题,勾股定理
解:把y=0代入
得 ,
解得 ,
∴A(-3,0),B(9,0),即可得AB=15,
∵又因D为AB的中点,
可得AD=BD=7.5,
求得OD=4.5,
在Rt△COD中,由勾股定理可得CD=7.5,故答案选D.
分析:令y=0,即可得到A和B的坐标,根据D为AB的中点,即可得到OD的长度,根据勾股定理求出CD即可。
6. A
考点:利用二次函数图象判断一元二次方程根的情况
解:∵抛物线 与 轴的交点的横坐标就是方程 的根,
∴ ( )的解是 .
故答案为:A.
分析:根据抛物线 与x轴的交点得横坐标就是方程 的根来解决此题.
7. B
考点:二次函数图象与坐标轴的交点问题
解:根据题意可得: ,
解得: .
故答案为:B.
分析:将二次函数图像与x轴的交点个数问题转化为一元二次方程根的判别式求解即可。
8. C
考点:二次函数图象与坐标轴的交点问题
解:当m=1时,函数解析式为:y=﹣6x+ 是一次函数,图象与x轴有且只有一个交点,
当m≠1时,函数为二次函数,
∵函数y=(m﹣1)x2﹣6x+ m的图象与x轴有且只有一个交点,
∴62﹣4×(m﹣1)× m=0,
解得,m=﹣2或3,
故答案为:C .
分析:本题需分类讨论,当m=1时,有且只有一个交点;当m≠1时,利用一元二次方程根的判别式求解即可。
9. C
考点:利用二次函数图象求一元二次方程的近似根
解:∵二次函数 的对称轴为 ,
而对称轴左侧图象与x轴交点横坐标的取值范围是 ,
∴右侧交点横坐标的取值范围是 .
故答案为:C.
分析:先根据图象得出对称轴左侧图象与x轴交点横坐标的取值范围,再利用对称轴 ,可以算出右侧交点横坐标的取值范围.
10. C
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征
解:①∵抛物线开口向上,∴ ,
∵抛物线对称轴在 轴的右侧,∴a,b异号,∴ ,
∵抛物线与 轴的交点在 轴上方,∴ ,
∴ ,所以①正确;
②∵图象与 轴交于两点 , ,其中 ,
∴ ,∴ ,
当 时, ,
∵当 时, ,
∴ ,∴ ,∴ ,故②正确;
③当 时, 值为 ,给 乘以4,即可化为 ,
∵当 时,由图象可知在 和x1之间 为正值,
当 时,在 和x1之间 为负值,
∴ 与0的关系不能确定,故③错误;
④∵ ,∴ ,∴ ,
即 ,∴ ,
∵ , ,∴ ,
∴ ,即 .
所以④正确.
综上,正确的是①②④,共3个,
故答案为:C.
分析:由于抛物线开口向上,可得,由抛物线对称轴在 轴的右侧,可得?,由抛物线与 轴的交点在 轴上方,可得, 据此判断①;由于图象与 轴交于两点 , ,其中 ?,从而可得, 当 时,, 求出, 从而可得,据此求出, 据此判断②;当 时, 值为 ,给 乘以4,即可化为 , 由于, 无法确定当时,所对抛物线上的点在x轴上方还是下方,据此判断③;由, 可得, 即得?,从而得出?,由于, 可得, 据此即可判断④.
二、填空题
11.
考点:二次函数图象与坐标轴的交点问题
解:当y=0时,2x2﹣3x﹣5=0,
解得,x1= ,x2=﹣1,
∵ ﹣(﹣1)= ,
∴抛物线y=2x2﹣3x﹣5与x轴两个交点之间的距离是 ,
故答案为: .
分析:由题意令y=0可得关于x的一元二次方程,解这个方程可求得抛物线与x轴的两个交点的横坐标,再根据数轴上两个点之间的距离等于两点坐标之差的绝对值可求解.
12. ①③④
考点:二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的图象
解:①∵二次函数的图象与x轴有两个交点,
∴b2﹣4ac>0,
即b2>4ac,故①正确;②∵抛物线的一个交点为(﹣3,0))对称轴为x=﹣1,
∴另一个交点为(1,0),
∴图象过点(1,0),不会经过(2,0),故②错误错误;③∵抛物线经过点(1,0),
∴y=a+b+c=0,故③正确;④∵抛物线开口向下,
∴a<0,
∵﹣ =﹣1,
∴b=2a,
∴a﹣b=a﹣2a=﹣a>0,故④正确;
故正确的为①③④,
故答案为①③④.
分析:①观察图像可知,二次函数的图象与x轴有两个交点,于是根据二次函数与一元二次方程的关系可得,b2﹣4ac>0,移项可得b2>4ac;
②由抛物线是轴对称图形可知,抛物线的对称轴与x轴的交点是抛物线与x轴的两个交点的中点,由线段中点得意义可求出抛物线与x轴的另一个交点坐标,结合选项可判断求解;
③由②的计算可知抛物线与x轴的另一个交点坐标为(1,0),把x=1代入解析式计算可求解;
④由图知,抛物线的对称轴是x=-1=-, 整理可求解.
13. m>1
考点:二次函数图象与坐标轴的交点问题
解:∵二次函数y=x2-2x+m的图象与x轴没有交点,
∴方程x2-2x+m=0没有实数根,
∴判别式△=(-2)2-4×1×m<0,
解得:m>1;
故答案为:m>1.
分析:将二次函数图像与x轴交点个数的问题转化为求一元二次方程根的个数的问题,即求根的判别式即可。
14. 5.8
考点:利用二次函数图象求一元二次方程的近似根
解:由表格可知,
当x=5时,y=-2.20<0,当x=6时,y=0.75>0,
则关于x的一元二次方程 的两个实数根中,其中的一个实数根约等于5.8(5.6至5.9均可),
故答案为:5.8.
分析:根据二次函数与一元二次方程近似根的关系,先找y的值,再判断即可。
15. m
解:二次函数 与 轴交点的横坐标为 、 ,将其图象往下平移2个单位长度可得出二次函数 的图象,如图所示:
观察图象,可知:m
分析:画出函数的草图,结合草图求解即可。
三、解答题
16. 解:令y=0,
∴ >0
∴无论m取何值,抛物线与x轴总有两个交点
考点:二次函数图象与坐标轴的交点问题
分析:将二次函数与x轴的交点问题转化为一元二次方程根的判别式求解即可。
17. (1)解: ,
, ,
二次函数 的图象与x轴有两个交点;
(2)解:当 时,二次函数为 ,令 ,
则 ,
解得 或 , 与x轴交点为 , ,
两交点间的距离为:
考点:二次函数图象与坐标轴的交点问题
分析:(1)利用根的判别式判断二次函数与x轴的交点坐标即可求解;
(2)先求出二次函数与x轴的交点坐标,再求两点之间的距离即可。
18. (1)∵抛物线解析式为y=(x+m)2+k的顶点为M(1,-4)
∴y=(x-1)2-4,抛物线对称轴是直线x=1.
∵a=1>0,
∴抛物线开口方向向上
(2)∵抛物线解析式为y=(x-1)2-4,
令y=0,得(x-1)2-4=0,
解得x1=3,x2=-1,
∴A(-1,0),B(3,0)
(3)∵△PAB与△MAB同底,且S△PAB=S△MAB ,
∴ =4,即yP=±4,
又∵点P在y=(x-1)2-4的图象上,yP≥-4,
∴yP=4,则(x-1)2-4=4,
解得x1= ,x2= ,
∴存在合适的点P,坐标为( ,4)或( ,4).
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征
分析:(1)根据抛物线的顶点坐标可以得到抛物线解析式,结合解析式写出抛物线的开口方向和对称轴;(2)由条件可先求得二次函数的解析式,再令y=0可求得A、B两点的坐标;(3)由条件可先求得P点的纵坐标,再代入解析式可求得P点坐标.
19. (1)解:设增加x棵桔子树.
由题意得
解之得x1=10,x2=130
∵成本最少,∴x=10
答:增加10棵桔子树时收益可以达到6650kg.
(2)设总的收益为W
则W= = =
∵10≤x≤40
∴当x=10时,Wmin=6650
当x=40时,Wmax=8000
答:果园最少产6650kg,最多产8000kg。
考点:二次函数图象与一元二次方程的综合应用,二次函数的其他应用
分析:(1)利用增加桔子树后:树的棵树×每一棵树的产量=6650,列方程即可求解。
(2)根据题意列出W与x的函数解析式,再将函数解析式转化为顶点式,然后利用二次函数的性质求解。
20. (1)解:因为当x=2时,y=﹣2<0,当x=3时,y=1>0,
所以可确定方程x2﹣2x﹣2=0的一个根x2所在的范围是2<x2<3;
(2)解:取x= =2.5,因为当x=2.5时,y<0.
又因为当x=3时,y>0,所以2.5<x2<3,
取x= =2.75,因为当x=2.75时,y>0.
又因为当x=2.5时,y<0,所以2.5<x2<2.75,
因为2.75﹣2.5= .
取x= =2.625,因为当x=2.625时,y<0.
又因为当x=2.75时,y>0,所以2.625<x2<2.75,
因为2,75﹣2,625= < ,
所以2.625<x2<2.75即为所求x2 的范围
考点:利用二次函数图象求一元二次方程的近似根
分析:(1)确定当x=2或 x=3时y的正负由此即可验证;(2)取第三步2和3的平均数x=2.5,计算y的值可得2.5<x2<3,再进一步取2.5和3的平均数x=2.75,计算y的值可得2.5<x2<2.75,再一次取平均数直到 即可
_21?????????è?????(www.21cnjy.com)_
