第一章 二次函数 单元测试(提高篇含解析)
文档属性
| 名称 | 第一章 二次函数 单元测试(提高篇含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 06:59:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学湘教版九年级下册第一章 二次函数 单元测试(提高篇)
一、单选题
1.下列关系中,是二次函数关系的是( ? ?)
A.?当距离S一定时,汽车行驶的时间t与速度v之间的关系。
B.?在弹性限度时,弹簧的长度y与所挂物体的质量x之间的关系。
C.?圆的面积S与圆的半径r之间的关系。
D.?正方形的周长C与边长a之间的关系。
2.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:①abc <0;②c+2a<0;③9a-3b+c=0; ④a-b≥m(am+b) (m为实数):⑤4ac-b2<0。
其中错误结论的个数有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.二次函数 ,当 且 时,y的最小值为 ,最大值为 ,则 的值为(???? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
4.已知x=m是一元二次方程x2+2x+n-3=0的一个根,则m+n的最大值等于(? )
A.???????????????????????????????????????B.?4??????????????????????????????????????C.???????????????????????????????????????D.?
5.已知二次函数y=ax2+2ax+2a+5(其中x是自变量)图象上有两点(﹣2,y1),(1,y2),满足y1 y2.当﹣2 x 1时,y的最小值为﹣5,则a的值为( )
?A.?-5?????????????????????????????????????????B.?-10?????????????????????????????????????????C.?-2?????????????????????????????????????????D.?5
6.我们定义一种新函数:形如 (a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:其中正确结论的个数是(?? )
①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);
②图象具有对称性,对称轴是直线x=1;
③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;
④当x=﹣1或x=3时,函数的最小值是0;
⑤当x=1时,函数的最大值是4,
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
7.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是(?? )
A.?y=?????????????????????????????B.??? y= ?????????????????????????????C.??? y= ?????????????????????????????D.?y=
8.在平面直角坐标系xOy中,点A坐标为 ,点B的坐标为 .将二次函数 的图象经过左(右)平移 个单位再上(下)平移 个单位得到图象M,使得图象M的顶点落在线段AB上.下列关于a,b的取值范围,叙述正确的是(??? )
A.? , ?????????????????????????????????????????B.? ,
C.? , ????????????????????????????????????????D.? ,
9.已知二次函数 (a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列4个判断中:①a+b=-1;②a>b﹣1;③b﹣a<0;④﹣1<a<﹣ ,正确的是( )
A.?①②③???????????????????????????B.?①②④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
10.如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为(? ?)
A.?4?????????????????????????????????????????B.?﹣4?????????????????????????????????????????C.?﹣6?????????????????????????????????????????D.?6
11.“闻起来臭,吃起来香”的臭豆腐是绍兴特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式: ? ( ? a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( ?? )?
?A.?3.50分钟????????????????????????????B.?4.05分钟????????????????????????????C.?3.75分钟????????????????????????????D.?4.25分钟
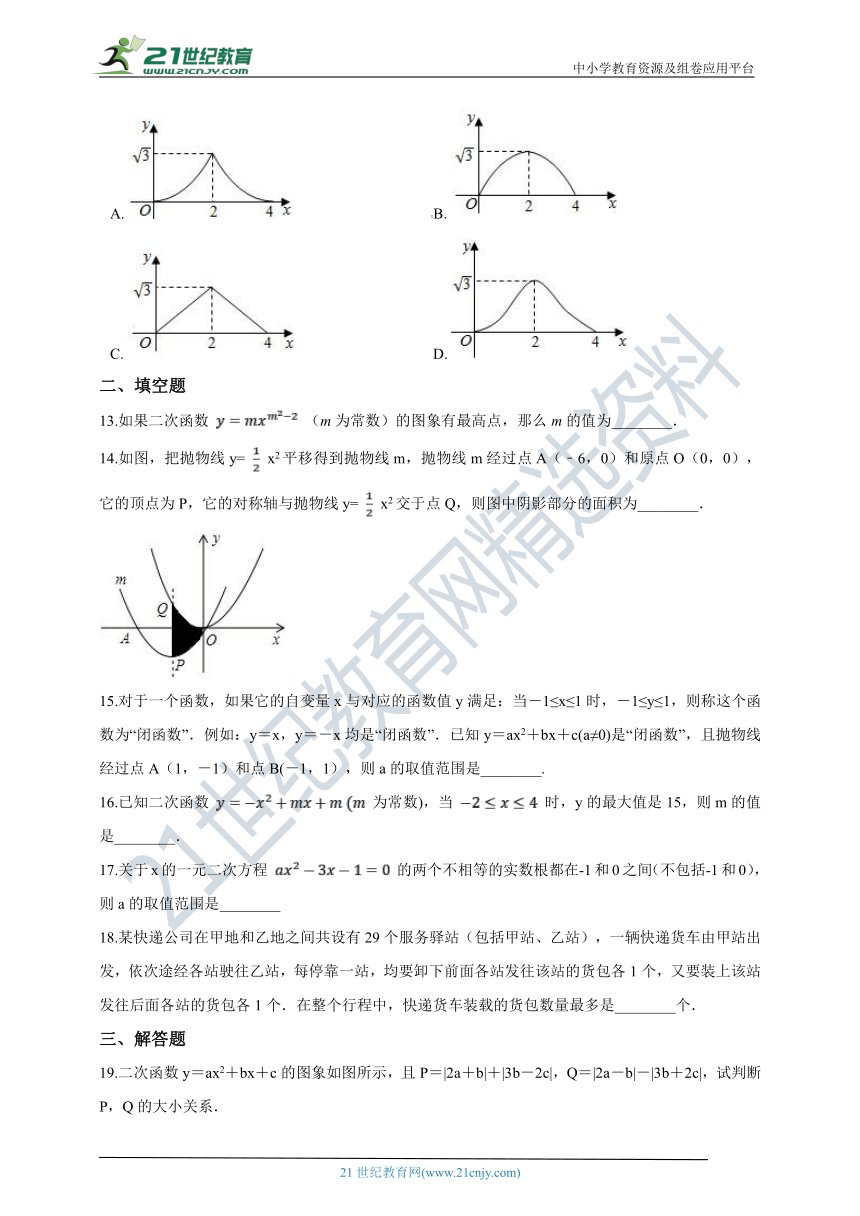
12.如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为(?? )
A.?????????????????????????????????????B.?
C.????????????????????????????????????D.?
二、填空题
13.如果二次函数 (m为常数)的图象有最高点,那么m的值为________.
14.如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为________.
15.对于一个函数,如果它的自变量x与对应的函数值y满足:当-1≤x≤1时,-1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=-x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,-1)和点B(-1,1),则a的取值范围是________.
16.已知二次函数 为常数),当 时,y的最大值是15,则m的值是________.
17.关于x的一元二次方程 的两个不相等的实数根都在-1和0之间(不包括-1和0),则a的取值范围是________
18.某快递公司在甲地和乙地之间共设有29个服务驿站(包括甲站、乙站),一辆快递货车由甲站出发,依次途经各站驶往乙站,每停靠一站,均要卸下前面各站发往该站的货包各1个,又要装上该站发往后面各站的货包各1个.在整个行程中,快递货车装载的货包数量最多是________个.
三、解答题
19.二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,试判断P,Q的大小关系.
20.已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
21.在平面直角坐标系xOy中,将点 定义为点 的“关联点”. 已知点 在函数 的图像上,将点A的“关联点”记为点 .
(1)请在如图基础上画出函数 的图像,简要说明画图方法;
(2)如果点 在函数 的图像上,求点 的坐标;
(3)将点 称为点 的“待定关联点”(其中 ),如果点 的“待定关联点” 在函数 的图像上,试用含 的代数式表示点 的坐标.
22.如图,在直角坐标系xOy中,二次函数y=x2+(2k- 1)x+k+1的图象与x轴相交于O、A两点
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由
23.如图,在平面直角坐标系中,抛物线y=ax2-2x+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、B的坐标分别为(-1,0),(3,0),点D为抛物线的顶点,抛物线的对称轴与直线BC相交于点E.
(1)求抛物线的解析式和点C的坐标;
(2)点P是直线BC下方的抛物线上一动点,当△PBC的面积最大时,请求出P点的坐标和△PBC的最大面积;
(3)点Q是线段BD上的一动点,将△DEQ沿边EQ翻折得到△ ,是否存在点Q使得△ 与△BEQ的重叠部分图形为直角三角形?若存在,请直接写出BQ的长,若不存在,请说明理由.
24.以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y= (a+c)x2-bx+ (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1 , 阴影面积为S2 , 求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
25.某公司有一块如图所示的平行四边形ABCD的绿化地,中间四边形EFGH是正方形,种上甲类花; AGD和 BEC是全等的等腰直角三角形,种上乙类花; ABH和 CDF是全等的直角三角形,种上丙类花;三类花的价格如下表:
花的种类 甲 乙 丙
价格(元/米2) 200 100 150
已知AH=3米,设BE的长为x米,绿化的总费用为y元.
(1)用含有x的代数式表示:EF=,FD=________;
(2)求y关于x的函数解析式及x的取值范围;
(3)如果FD的长比CF至少多4米,求总费用y的最小值.
26.知识链接:弹道导弹飞行轨迹可以分为三个阶段.第一阶段:导弹点火后,垂直向上飞行阶段;第二阶段:导弹进入安全预定高度,以曲线路线飞行阶段(最高点称为轨道的远地点);第三阶段:发动机熄火后,导弹弹头与弹体分离,以惯性飞向目标阶段.
某洲际导弹发射后,计算机隔一段时间(单位:分)对导弹离地高度(单位:千米)进行数据采集,对这些数据进行列表统计后得到如下表格:
时间 0 1 2 4 5 6 9 13 14 16 19 24 …
离地高度 0 24 96 386 514 616 850 994 1000 976 850 400 …
已知导弹在第 分钟( 为整数)开始进入飞行第二阶段,在下落过程中距离地面100千米时进入第三阶段.
(1)该导弹在发射多少时间后达到轨道的远地点,此时距离地面的高度是多少千米?
(2)请用学过的函数模型来确定第二阶段的曲线解析式,并求出 的值.
(3)求导弹发射多少时间后发动机熄火?(结果保留根号)
答案解析部分
一、单选题
1. C
考点:二次函数的定义
解:由题意,A的解析式为 ,B的解析式为 ,C的解析式为 ,D的解析式为 ,唯有B是二次函数关系,故选C.
分析:能够运用实际问题的意义列出正确的解析式,并进行分析判断是否是二次函数,要根据二次函数的定义的基本要求.
2. A
考点:二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
解:①根据抛物线可知,a>0,c<0
对称轴x=-<0
∴b>0
∴abc<0,即①正确;
②根据对称轴可得,-=-1
∴b=2a
∵x=1时,y=a+b+c=0
∴c+3a=0
∴c+2a=-3a+2a=-a<0,即②正确;
③(1,0)关于x=-1的对称点为(-3,0)
∴x=-3时,y=9a-3b+c=0,即③正确
④当x=-1时,y的最小值为a-b+c
∴x=m时,y=am2+bm+c
∴am2+bm+c≥a-b+c
即a-b≤m(am+b),即④错误;
⑤∵抛物线与x轴有两个交点
∴△>0
∴b2-4ac>0
∴4ac-b2<0,即⑤正确
故答案为:A.
分析:根据二次函数的图象和性质,分别进行判断得到答案即可。
3. D
考点:二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
解:二次函数 的大致图象如解图,
∵ ,且 ,
∴ , ,
①当 时,当 时,y取最小值,即 ,
解得 (舍去)或 ;
当 时,y取最大值,即 ,
解得 (舍去)或 (舍去);
②当 时,当 时y取最小值,即 ,
解得 (舍去)或 ;
当 时,y取最大值,即 ,
解得 ,
∴ .
故答案为:D.
分析:由 ,且 , 可得 , , 分两种情况①当 时,得出当 时,y取最小值,当 时,y取最大值;②当 时,得出当 时y取最小值当 时,y取最大值,据此分别解答即可.
4. A
考点:一元二次方程的根,一元二次方程根的判别式及应用,二次函数y=ax^2+bx+c的性质
解:由题意得:此方程的根的判别式 ,
解得 ,
是一元二次方程 的一个根,
,即 ,
对于任意实数m, 均成立,
令 ,
整理得: ,
由二次函数的性质可知,当 时,y取得最大值,最大值为 ,
即 的最大值等于 ,
故答案为:A.
分析:由 x=m是方程的根和一元二次方程根的判别式可得m,n的范围和 , 根据二次函数的性质可得最大值.
5. C
考点:二次函数的最值,二次函数y=ax^2+bx+c的性质
解: y=ax2+2ax+2a+5 ,
=a(x+1)2+a+5,
∵对称轴x=-1,?
∴ (﹣2,y1)离对称轴较近,(1,y2),离对称轴较远,
∵ y1??y2 ,
∴a<0,
当-2≤x≤1时,x=1取最小值,
即二次函数经过(1,-5),
∴-5=a+2a+2a+5,
∴a=-2.
故答案为:C.
分析:首先配方求出抛物线的对称轴方程,比较两点离对称轴的远近,结合其函数值的大小得出a<0,从而由函数的性质可知当x=1取最小值,把最小值代入函数式即可求出a值.
6. A
考点:二次函数的最值,二次函数图象与坐标轴的交点问题,二次函数y=ax^2+bx+c的性质
解:如图:
①∵(-1,0),(3,0)和(0,3)坐标都满足函数 ,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线 ,因此②也是正确的;
③根据函数的图象和性质,发现当 或 时,函数值y随x值的增大而增大,因此③也是正确的;
④函数图象的最低点就是与x轴的两个交点,根据y=0,求出相应的x的值为 或 ,因此④也是正确的;
⑤从图象上看,存在函数值要大于当 时的 ,因此⑤是不正确的.
故答案为:A.
分析:由y=0,建立关于x的方程,解方程求出x的值,就可得到图象与x轴的交点坐标,由x=0求出y的值,可得到图象与y轴的交点坐标,可对①作出判断;利用对称轴方程,可得到抛物线的对称轴,可对②作出判断;利用二次函数的性质,可得到函数值y随x值的增大而增大时自变量x的取值范围可对③作出判断;观察函数图象,利用函数解析式可求出函数的最小值为0时自变量x的值,可对④作出判断;由图象可知函数的最大值不能确定,可对⑤作出判断,综上所述可得到正确结论的个数.
7. C
考点:根据实际问题列二次函数关系式
解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,
∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE
∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2 , 即(3a)2+(4a)2=x2 ,
解得:a= ,
∴y=S四边形ABCD=S梯形ACDE= ×(DE+AC)×DF
= ×(a+4a)×4a
=10a2= x2 .
故答案为:C.
分析:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,利用AAS判定△ABC和△ADE全等,然后利用全等三角形的性质得出BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,CF=AC﹣AF=AC﹣DE=3a,利用勾股定理求出a与x的关系,分别用含x的代数式表示出DE、DF、AC,求出梯形AEDC的面积即为四边形ABCD的面积。
?8. B
考点:二次函数图象的几何变换,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的性质
解:∵ = ,
∴二次函数的顶点坐标为(1,-2),
∵点A坐标为 ,点B的坐标为 ,
∴二次函数图象是向左平移a个单位,再向上平移b个单位得到图象M,
∴平移后的顶点坐标为(1-a,-2+b)
∵图象M的顶点落在线段AB上,
∴-2≤1-a≤0,2≤-2+b≤3,
解得:1≤a≤3,4≤b≤5,
故答案为:B.
分析:先求出二次函数 = 的顶点坐标(1,-2),根据题意,二次函数图象是向左平移a个单位,再向上平移b个单位得到图象M,平移后的顶点坐标为(1-a,-2+b),进而得到满足条件的a、b的不等式,解之即可.
9. B
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的性质
解:①将(1,0)代入解析式,得 ,即a+b=-1,
故①符合题意;
②∵a<0
∴抛物线在对称轴左侧时,y随x的增大而增大
∵﹣2<x1<﹣1,另一交点为(1,0)
∴
∴当x=-1时,y>0,即
∴
故②符合题意;
③,由②得知 ,且a<0
∴ ,即
故③不符合题意;
④由根与系数的关系得到
∴
∴ ,解得﹣1<a<﹣
故④符合题意.
故答案为:B.
分析: 将(1,0)代入中,可得 , 据此判断①;由于a<0,可得抛物线在对称轴左侧时,y随x的增大而增大,由﹣2<x1<﹣1,另一交点为(1,0),可得 , 从而求出当x=-1时,y=? , 据此判断②;由且a<0,可得 , 据此判断③;由根与系数的关系得到 , 从而求出 , 即得 , 求出a的范围判断④即可.
10. C
考点:待定系数法求二次函数解析式,二次函数图象与坐标轴的交点问题,图形的旋转
解:当y=0时,﹣x(x﹣5)=0,解得x 1=0,x 2=5,则A 1(5,0),
∴OA1=5,
∵将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…;如此进行下去,得到一“波浪线”,
∴A1A2=A2A3=…=OA1=5,
∴抛物线C404的解析式为y=(x﹣5×403)(x﹣5×404),即y=(x﹣2015)(x﹣2020),
当x=2018时,y=(2018﹣2015)(2018﹣2020)=﹣6,
即m=﹣6.
故答案为:C
分析:先求出抛物线C1与x轴的交点坐标,观察图形可知第奇数个抛物线都在x轴上方,第偶数个抛物线都在x轴下方,2018÷5=403·····3,可判断点P在第404个抛物线上,用待定系数法先求出该抛物线的解析式,然后把点P的坐标代入计算即可得解.
11. C
考点:二次函数的最值,待定系数法求二次函数解析式
解:由题意知,函数p=at2+bt+c,
∴,
解得,
∴p=0.25t2+1.5t-1.7=-0.2(t-3.75)2+0.2×3.752-1.7
=-0.2(t-3.75)2+1.1125.
故当t=3.75时,p有最大值.
故答案为:C.
分析:利用待定系数法求出函数解析式,配方求出顶点坐标,即可得出加工煎炸臭豆腐的最佳时间.
12. A
考点:二次函数的实际应用-几何问题
解:C点移动到F点,重叠部分三角形的边长为x,由于是等边三角形,则高为 ,面积为y=x· · = ,
B点移动到F点,重叠部分三角形的边长为(4-x),高为 ,面积为
y=(4-x)· · = ,
两个三角形重合时面积正好为 .
由二次函数图象的性质可判断答案为A,
故答案为:A.
分析:根据图象可得出重叠部分三角形的边长为x,根据特殊角三角函数可得高为 ,由此得出面积y是x的二次函数,直到重合面积固定,再往右移动重叠部分的边长变为(4-x),同时可得
二、填空题
13. -2
考点:二次函数的定义
解:∵二次函数 (m为常数)的图象有最高点,
∴
解得:m=-2,
故答案为-2.
分析:根据二次函数的定义结合其有最高点确定m的值即可.
14.
考点:二次函数图象与几何变换
解:过点P作PM⊥y轴于点M,
∵抛物线平移后经过原点O和点A(﹣6,0),
∴平移后的抛物线对称轴为x=﹣3,
得出二次函数解析式为:y= (x+3)2+h,
将(﹣6,0)代入得出:
0= (﹣6+3)2+h,
解得:h=﹣ ,
∴点P的坐标是(﹣3,﹣ ),
根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO的面积,
∴S=|﹣3|×|﹣ |= .
故答案为: .
分析:可转化阴影部分面积,进行分割,根据两抛物线形状相同,具有对称性,因此把x轴上侧的阴影面积补到下侧空白部分,构成完整的矩形.
15. - ≤a<0或0<a≤
考点:二次函数图象与系数的关系
解:将A、B两点代入抛物线,可得出b=-1,a+c=0,
所以抛物线为y=ax2-x-a(a≠0)
对称轴为
a<o,抛物线开口向下,对称轴<0
因为抛物线经过A、B
画图可得出当对称<0或≥1时,符合题意,a的趋势范围为
分析:将A、B两点代入,求得解析式,再根据对称轴进行判断。
16. 6和-19
考点:待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质
解:二次函数y=-x2+mx+m=-(x- )2+ +m,
当4< 时,即m>8,
在-2≤x≤4时,x=4时取得最大值,则15=-42+4m+m,得m=6.2(舍去);
当 <-2时,即m<-4,
在-2≤x≤4时,x=-2时取得最大值,则15=-22-2m+m,得m=-19,
当-2≤ ≤4时,即-4≤m≤8,
在-2≤x≤4时,x= 时取得最大值,则15= +m,得m1=6,m2=-10(舍去),
由上可得,m的值是6和-19,
故答案为:6和-19.
分析:根据题目中的函数解析式和当-2≤x≤4时,y的最大值是15,利用分类讨论的方法可以求得m的值,本题得以解决.
17.考点:一元二次方程根的判别式及应用,二次函数图象与坐标轴的交点问题
解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根
∴△=(-3)2-4×a×(-1)>0,
解得:a>?
设f(x)=ax2-3x-1,如图,
∵实数根都在-1和0之间,
∴-1<? <0,
∴a<? ,
且有f(-1)<0,f(0)<0,
即f(-1)=a×(-1)2-3×(-1)-1<0,f(0)=-1<0,
解得:a<-2,
∴? <a<-2,
故答案为:? <a<-2.
分析:首先根据根的情况利用判别式解得a的取值范围,然后根据已知中两个根的范围可知两个根的和大于-1且小于0,求出a的范围,画出草图可观察到x=1和x=0时ax2-3x-1的值都小于0,据此即可确定出a的范围.
18. 210
考点:待定系数法求二次函数解析式,探索数与式的规律,二次函数的其他应用
解:当一辆快递货车停靠在第x个服务驿站时,
快递货车上需要卸下已经通过的(x﹣1)个服务驿站发给该站的货包共(x﹣1)个,
还要装上下面行程中要停靠的(n﹣x)个服务驿站的货包共(n﹣x)个.
根据题意,完成下表:
服务驿站序号 在第x服务驿站启程时快递货车货包总数
1 n﹣1
2 (n﹣1)﹣1+(n﹣2)=2(n﹣2)
3 2(n﹣2)﹣2+(n﹣3)=3(n﹣3)
4 3(n﹣3)﹣3+(n﹣4)=4(n﹣4)
5 4(n﹣4)﹣4+(n﹣5)=5(n﹣5)
… …
n 0
由上表可得y=x(n﹣x).当n=29时,y=x(29﹣x)=﹣x2+29x=﹣(x﹣14.5)2+210.25,
当x=14或15时,y取得最大值210.
答:在整个行程中,快递货车装载的货包数量最多是210个.
故答案为:210.
分析:根据理解题意找出题目中所给的等量关系,找出规律,写出货包数量的函数解析式,再根据二次函数最值的求法求出快递货车装载的货包数量最多的站.
三、解答题
19. 解:∵抛物线的开口向下,∴a<0.∵ >0,∴b>0,∴2a-b<0.∵ =1,∴b+2a=0.当x=-1时,y=a-b+c<0,∴- b-b+c<0,∴3b-2c>0.∵抛物线与y轴的正半轴相交,∴c>0,∴3b+2c>0,∴P=3b-2c,Q=b-2a-3b-2c=-2a-2b-2c,∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-4b<0.∴P>Q.
考点:二次函数图象与系数的关系
分析:根据抛物线的开口向下得出a<0,由抛物线的对称轴在y轴的右侧,知a,b异号,根据抛物线的对称轴直线是1,得出b+2a=0,当x=-1时,y=a-b+c<0,故3b-2c>0,根据抛物线与y轴的正半轴相交,得出c>0,故3b+2c>0,然后根据绝对值的意义,去掉绝对值符号,再按整式加减的方法分别化简P,Q的值,再利用作差法,即可得出P,Q的大小。
20. 解:(Ⅰ)当a=b=1,c=﹣1时,抛物线为y=3x2+2x﹣1,方程3x2+2x﹣1=0的两个根为x1=﹣1, .∴该抛物线与x轴公共点的坐标是(﹣1,0)和( ,0);(Ⅱ)当a=b=1时,抛物线为y=3x2+2x+c,且与x轴有公共点.对于方程3x2+2x+c=0,判别式△=4﹣12c≥0,有c≤ .①当 时,由方程3x2+2x+ =0,解得x1=x2=﹣ .此时抛物线为y=3x2+2x+ 与x轴只有一个公共点(﹣ ,0);②当 时,x1=﹣1时,y1=3﹣2+c=1+c;x2=1时,y2=3+2+c=5+c.由已知﹣1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为 ,应有 即 ,解得﹣5<c≤﹣1.综上, 或﹣5<c≤﹣1.(6分)(Ⅲ)对于二次函数y=3ax2+2bx+c,由已知x1=0时,y1=c>0;x2=1时,y2=3a+2b+c>0,又∵a+b+c=0,∴3a+2b+c=(a+b+c)+2a+b=2a+b.∴2a+b>0.∵b=﹣a﹣c,∴2a﹣a﹣c>0,即a﹣c>0.∴a>c>0.(7分)∵关于x的一元二次方程3ax2+2bx+c=0的判别式△=4b2﹣12ac=4(a+c)2﹣12ac=4[(a﹣c)2+ac]>0,∴抛物线y=3ax2+2bx+c与x轴有两个公共点,顶点在x轴下方.又该抛物线的对称轴 ,由a+b+c=0,c>0,2a+b>0,得﹣2a<b<﹣a,∴ .又由已知x1=0时,y1>0;x2=1时,y2>0,观察图象,
可知在0<x<1范围内,该抛物线与x轴有两个公共点.
考点:二次函数图象与坐标轴的交点问题
分析:(Ⅰ)把a,b,c的值代入可得抛物线的解析式,然后令y=0可得到关于x的方程,然后求得方程的两根,从而可得到抛物线与x轴交点坐标;
(Ⅱ)把a,b代入可得到抛物线的解析式,然后可求得抛物线的对称轴为x=- , 然后再分为△=0和△>0两种情况求解即可;
(Ⅲ)抛物线y=3ax2+2bx+c与x轴公共点的个数就是一元二次方程3ax2+2bx+c=0的实数根的个数,接下来,判断出方程3ax2+2bx+c=0根的判别式的符号,依据判别式的符号得出相应的结论.
21. (1)解:如图
将图9中的抛物线 向下平移2个单位长,可得抛物线
画法:①列表;②描点(五点画图法);③用光滑的曲线连接这五个点.
(2)解:由题意,得点 的“关联点”为
由点 在抛物线 上,可得 ,
又∵ 在抛物线 上,∴
解得 .将 代入 ,得
(3)解:点 的“待定关联点”为 ,
∵ 在抛物线 的图像上,∴ .
∴ , .又∵ ,∴ .
?当 时, ,故可得
考点:二次函数图象的几何变换,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的图象
分析:(1)利用图像的平移规律,将 向下平移2个单位长度即可得到 (2)先根据题意求出 ,再代入到 中,联合A代入到 即可求出答案.(3)将 代入 中解出x的值,可点 的坐标即可用含n的代数式表示.
22. (1)解: 函数的图象与x轴相交于O,.
,
二次函数的解析式为y=x-3x.
(2)解:假设存在点 ,过点 作 轴于点 , 的面积等于6,。
.
当 时, ,解得 或3
, ,即 ,解得 或 (舍去).
又 顶点坐标为 , , ? 下方不存在 点.
点 的坐标为
(3)解: 点 的坐标为 , , ?当 时, .
设P点横坐标为 ,则纵坐标为 ,即 ,解得 或 .
在抛物线上仅存在一点
的面积为:
考点:二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
分析:(1)将原点的坐标代入抛物线,即可得到k的值;
(2)根据得到的抛物线的解析式求出点A的坐标,即可得到OA的长度,根据△OAB的面积求出B点纵坐标的绝对值,代入抛物线中,计算得到点B的坐标即可;
(3)根据点B的坐标计算直线OB的解析式,求出点P的坐标特点,代入解析式计算得到坐标即可。计算△POB的面积,求出OB和OP的长度,即可得到答案。
23. (1)解:将点A(-1,0)、B(3,0)代入抛物线解析式y=ax2-2x+c可得:
,解得: ,
∴抛物线的解析式为y=x2-2x-3,
当x=0时,y=-3,所以C的坐标为C(0,-3)
(2)解:∵B(3,0),C(0,-3),可得直线BC解析式为:y=x-3,
设与直线BC平行且在BC下方的一条直线l解析式为y=x+b,当直线l与抛物线只有一个交点时,△PBC的面积最大,
联立解析式 ,
可得 ,
整理得: ,
∴ ,解得:b= ,
即 ,解得:x= ,将x= 代入抛物线解析式可得 ,
所以P ,
如图1,过点P作PM⊥y轴于M,∴M(0, ),
∴
∴△PBC的最大面积为
(3) 或 或 .
考点:待定系数法求二次函数解析式,翻折变换(折叠问题),相似三角形的判定与性质,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的性质
解:(3)根据(1)中解析式可得:D(1,-4),直线x=1交x轴于F,BD= ,
分类讨论:
①如图3,EQ⊥DB于Q,△DEQ沿边EQ翻折得到△D’EQ,
∵∠EDQ=∠BDF,
∴Rt△DEQ∽Rt△DBF,
∴ ,即 ,
解得DQ= ,
∴BQ=BD?DQ=
②如图4, ED′⊥BD于H,
∵∠EDH=∠BDF,
∴Rt△DEH∽Rt△DBF,
∴ ,即 ,
解得DH= ,EH= ,
在Rt△QHD′中,设QH=x,D′Q=DQ=DH?HQ=
, D′H=D′E?EH=DE?EH=2? ,
∴ ,解得x=1? ,
∴BQ=BD?DQ=BD?(DH?HQ)=BD?DH+HQ= ,;
③如图5,D′Q⊥BC于G,作EI⊥BD于I,易得EI= ,BI= ,
∵△DEQ沿边EQ翻折得到△D′EQ,
∴∠EQD=∠EQD′,
∴EG=EI= ,
∵BE= ,
∴BG=BE?EG=
∵∠GBQ=∠IBE,
∴△BQG∽△BEI,
∴ ,即
∴BQ=
综上所述,当BQ为 或 或 时,将△DEQ沿边EQ翻折得到△D′EQ,使得△D′EQ与△BEQ的重叠部分图形为直角三角形.
?
分析:(1)将点A(-1,0)、B(3,0)代入抛物线解析式可求出a,c的值,得到抛物线的解析式,令x=0可求出c的坐标;(2)直线BC解析式为:y=x-3,设与直线BC平行且在BC下方的一条直线l解析式为y=x+b,当直线l与抛物线只有一个交点时,△PBC的面积最大,联立解析式,求出当 时x的值,即为P点横坐标,再根据分割面积法求出此时 ;(3)根据(1)中解析式可得:D(1,-4),直线x=1交x轴于F,BD= ,然后分情况讨论,分别求出BQ的长即可.]
24. (1)证明:因为二次函数y= (a+c)x2-bx+ (c-a)的顶点在x轴上,
∴Δ=0,即:b2-4× (a+c)× (c-a)=0,
∴c2=a2+b2 ,
得∠ACB=90°.
(2)解:∵z2+z-20=0.
∴z1=-5,z2=4,
∵a>0,得a=4.
设b=AC=2x,有S△ABC= AC·BC=4x,S半圆= p ?x2
∴S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆=- x2+4x
(3)解: S2-S1=- (x- )2+ ,
∴当x= 时,(S2-S1)有最大值 .
这时,b= ,a=4,c= ,
如图,连接
为圆的直径,
?
?
?
?
?BD= .
当BD为 时,(S2-S1)最大.
考点:根据实际问题列二次函数关系式,相似三角形的判定与性质,利用二次函数图象判断一元二次方程根的情况
分析:(1)由抛物线的顶点在x轴上,得到 从而可得结论.(2)利用a是z2+z-20=0的根,求解 的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆 , 从而可得答案,(3)由(2)的函数关系式求解( )最大时 ,利用直径所对的圆周角是直角,得到 利用相似三角形的性质可得答案.
25. (1)x-3,2x-3
(2)解:由题意得:
y=200(x-3)2+100× x2×2+150× ×3×(2x-3)×2
=200(x-3)2+100x2+450(2x-3)
=300x2-300x+450,
∴y=300x2-300x+450(x>3)
(3)解:由题意得:2x-3≥3+4,
解得:x≥5,
∵y=300x2-300x+450(x>3);
∴y=300(x- )2+375
∵a=300>0,对称轴为直线x= ,
∴当x> 时,y随着x的增大而增大,
又∵x≥5,
∴当x=5时,y取得最小值,最小值为6450,
答:总费用y的最小值为6450元.
考点:二次函数的实际应用-几何问题
解:(1)∵ ABH和 CDF是全等的直角三角形,AH=3米,
∴CF=AH=3米,
∵ AGD和 BEC是全等的等腰直角三角形,BE=x米,
∴AG=GD=EC=BE=x米,
∴EF=EC-CF=x-3,
∵四边形EFGH是正方形,
∴FG=EF=x-3,
∴FD=FG+GD
=x-3+x
=2x-3,
故答案为:x-3,2x-3;
分析:(1)由题意可得CF=AH=3米,AG=GD=EC=BE=x米,由此可得EF=EC-CF=x-3,再由正方形EFGH可得FG=EF=x-3,由此即可表示出FD的长;(2)根据总费用等于各部分的费用之和即可列出y关于x的函数解析式;(3)由2x-3≥3+4可得x≥5,由y=300x2-300x+450可得y=300(x- )2+375,再根据二次函数的增减性即可求得x≥5的y的最小值.
26. (1)解:根据表格中的数据可知,发射14分时到达轨道的远地点,此时距离地面的高度为1000千米.
(2)解:根据表中数据可知第二阶段的曲线为抛物线,
可设抛物线为 ,将点 代入,
∴ ,
解得: ,
∴抛物线的解析式为: ,
当 ,1,2,4,5时, 依次为 , ,136,400,514.
∴ .
∴导弹在第5分钟开始进入飞行第二阶段;
(3)解:令 ,则 ,
解得: , (不合题意,舍去).
答:导弹发射 分钟熄火.
考点:二次函数的其他应用
分析:(1)根据表格的数据,即可得到答案;
(2)结合表格中的数据,设函数解析式为 ,利用待定系数法进行解题,即可求出答案;
(3)令 ,代入函数解析式,即可求出答案.
_21?????????è?????(www.21cnjy.com)_
初中数学湘教版九年级下册第一章 二次函数 单元测试(提高篇)
一、单选题
1.下列关系中,是二次函数关系的是( ? ?)
A.?当距离S一定时,汽车行驶的时间t与速度v之间的关系。
B.?在弹性限度时,弹簧的长度y与所挂物体的质量x之间的关系。
C.?圆的面积S与圆的半径r之间的关系。
D.?正方形的周长C与边长a之间的关系。
2.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:①abc <0;②c+2a<0;③9a-3b+c=0; ④a-b≥m(am+b) (m为实数):⑤4ac-b2<0。
其中错误结论的个数有(??? )
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
3.二次函数 ,当 且 时,y的最小值为 ,最大值为 ,则 的值为(???? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
4.已知x=m是一元二次方程x2+2x+n-3=0的一个根,则m+n的最大值等于(? )
A.???????????????????????????????????????B.?4??????????????????????????????????????C.???????????????????????????????????????D.?
5.已知二次函数y=ax2+2ax+2a+5(其中x是自变量)图象上有两点(﹣2,y1),(1,y2),满足y1 y2.当﹣2 x 1时,y的最小值为﹣5,则a的值为( )
?A.?-5?????????????????????????????????????????B.?-10?????????????????????????????????????????C.?-2?????????????????????????????????????????D.?5
6.我们定义一种新函数:形如 (a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:其中正确结论的个数是(?? )
①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);
②图象具有对称性,对称轴是直线x=1;
③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;
④当x=﹣1或x=3时,函数的最小值是0;
⑤当x=1时,函数的最大值是4,
A.?4???????????????????????????????????????????B.?3???????????????????????????????????????????C.?2???????????????????????????????????????????D.?1
7.如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是(?? )
A.?y=?????????????????????????????B.??? y= ?????????????????????????????C.??? y= ?????????????????????????????D.?y=
8.在平面直角坐标系xOy中,点A坐标为 ,点B的坐标为 .将二次函数 的图象经过左(右)平移 个单位再上(下)平移 个单位得到图象M,使得图象M的顶点落在线段AB上.下列关于a,b的取值范围,叙述正确的是(??? )
A.? , ?????????????????????????????????????????B.? ,
C.? , ????????????????????????????????????????D.? ,
9.已知二次函数 (a<0)的图象过点(1,0)和(x1 , 0),且﹣2<x1<﹣1,下列4个判断中:①a+b=-1;②a>b﹣1;③b﹣a<0;④﹣1<a<﹣ ,正确的是( )
A.?①②③???????????????????????????B.?①②④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
10.如图,一段抛物线:y=﹣x(x﹣5)(0≤x≤5),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…如此进行下去,得到一“波浪线”,若点P(2018,m)在此“波浪线”上,则m的值为(? ?)
A.?4?????????????????????????????????????????B.?﹣4?????????????????????????????????????????C.?﹣6?????????????????????????????????????????D.?6
11.“闻起来臭,吃起来香”的臭豆腐是绍兴特色小吃,臭豆腐虽小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把焦脆而不糊的豆腐块数的百分比称为“可食用率”,在特定条件下,“可食用率”p与加工煎炸的时间t(单位:分钟)近似满足函数关系式: ? ( ? a,b,c为常数),如图纪录了三次实验数据,根据上述函数关系和实验数据,可以得到加工煎炸臭豆腐的最佳时间为( ?? )?
?A.?3.50分钟????????????????????????????B.?4.05分钟????????????????????????????C.?3.75分钟????????????????????????????D.?4.25分钟
12.如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为(?? )
A.?????????????????????????????????????B.?
C.????????????????????????????????????D.?
二、填空题
13.如果二次函数 (m为常数)的图象有最高点,那么m的值为________.
14.如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为________.
15.对于一个函数,如果它的自变量x与对应的函数值y满足:当-1≤x≤1时,-1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=-x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,-1)和点B(-1,1),则a的取值范围是________.
16.已知二次函数 为常数),当 时,y的最大值是15,则m的值是________.
17.关于x的一元二次方程 的两个不相等的实数根都在-1和0之间(不包括-1和0),则a的取值范围是________
18.某快递公司在甲地和乙地之间共设有29个服务驿站(包括甲站、乙站),一辆快递货车由甲站出发,依次途经各站驶往乙站,每停靠一站,均要卸下前面各站发往该站的货包各1个,又要装上该站发往后面各站的货包各1个.在整个行程中,快递货车装载的货包数量最多是________个.
三、解答题
19.二次函数y=ax2+bx+c的图象如图所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,试判断P,Q的大小关系.
20.已知抛物线y=3ax2+2bx+c,
(Ⅰ)若a=b=1,c=﹣1,求该抛物线与x轴公共点的坐标;
(Ⅱ)若a=b=1,且当﹣1<x<1时,抛物线与x轴有且只有一个公共点,求c的取值范围;
(Ⅲ)若a+b+c=0,且x1=0时,对应的y1>0;x2=1时,对应的y2>0,试判断当0<x<1时,抛物线与x轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
21.在平面直角坐标系xOy中,将点 定义为点 的“关联点”. 已知点 在函数 的图像上,将点A的“关联点”记为点 .
(1)请在如图基础上画出函数 的图像,简要说明画图方法;
(2)如果点 在函数 的图像上,求点 的坐标;
(3)将点 称为点 的“待定关联点”(其中 ),如果点 的“待定关联点” 在函数 的图像上,试用含 的代数式表示点 的坐标.
22.如图,在直角坐标系xOy中,二次函数y=x2+(2k- 1)x+k+1的图象与x轴相交于O、A两点
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;
(3)对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由
23.如图,在平面直角坐标系中,抛物线y=ax2-2x+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、B的坐标分别为(-1,0),(3,0),点D为抛物线的顶点,抛物线的对称轴与直线BC相交于点E.
(1)求抛物线的解析式和点C的坐标;
(2)点P是直线BC下方的抛物线上一动点,当△PBC的面积最大时,请求出P点的坐标和△PBC的最大面积;
(3)点Q是线段BD上的一动点,将△DEQ沿边EQ翻折得到△ ,是否存在点Q使得△ 与△BEQ的重叠部分图形为直角三角形?若存在,请直接写出BQ的长,若不存在,请说明理由.
24.以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y= (a+c)x2-bx+ (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1 , 阴影面积为S2 , 求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
25.某公司有一块如图所示的平行四边形ABCD的绿化地,中间四边形EFGH是正方形,种上甲类花; AGD和 BEC是全等的等腰直角三角形,种上乙类花; ABH和 CDF是全等的直角三角形,种上丙类花;三类花的价格如下表:
花的种类 甲 乙 丙
价格(元/米2) 200 100 150
已知AH=3米,设BE的长为x米,绿化的总费用为y元.
(1)用含有x的代数式表示:EF=,FD=________;
(2)求y关于x的函数解析式及x的取值范围;
(3)如果FD的长比CF至少多4米,求总费用y的最小值.
26.知识链接:弹道导弹飞行轨迹可以分为三个阶段.第一阶段:导弹点火后,垂直向上飞行阶段;第二阶段:导弹进入安全预定高度,以曲线路线飞行阶段(最高点称为轨道的远地点);第三阶段:发动机熄火后,导弹弹头与弹体分离,以惯性飞向目标阶段.
某洲际导弹发射后,计算机隔一段时间(单位:分)对导弹离地高度(单位:千米)进行数据采集,对这些数据进行列表统计后得到如下表格:
时间 0 1 2 4 5 6 9 13 14 16 19 24 …
离地高度 0 24 96 386 514 616 850 994 1000 976 850 400 …
已知导弹在第 分钟( 为整数)开始进入飞行第二阶段,在下落过程中距离地面100千米时进入第三阶段.
(1)该导弹在发射多少时间后达到轨道的远地点,此时距离地面的高度是多少千米?
(2)请用学过的函数模型来确定第二阶段的曲线解析式,并求出 的值.
(3)求导弹发射多少时间后发动机熄火?(结果保留根号)
答案解析部分
一、单选题
1. C
考点:二次函数的定义
解:由题意,A的解析式为 ,B的解析式为 ,C的解析式为 ,D的解析式为 ,唯有B是二次函数关系,故选C.
分析:能够运用实际问题的意义列出正确的解析式,并进行分析判断是否是二次函数,要根据二次函数的定义的基本要求.
2. A
考点:二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
解:①根据抛物线可知,a>0,c<0
对称轴x=-<0
∴b>0
∴abc<0,即①正确;
②根据对称轴可得,-=-1
∴b=2a
∵x=1时,y=a+b+c=0
∴c+3a=0
∴c+2a=-3a+2a=-a<0,即②正确;
③(1,0)关于x=-1的对称点为(-3,0)
∴x=-3时,y=9a-3b+c=0,即③正确
④当x=-1时,y的最小值为a-b+c
∴x=m时,y=am2+bm+c
∴am2+bm+c≥a-b+c
即a-b≤m(am+b),即④错误;
⑤∵抛物线与x轴有两个交点
∴△>0
∴b2-4ac>0
∴4ac-b2<0,即⑤正确
故答案为:A.
分析:根据二次函数的图象和性质,分别进行判断得到答案即可。
3. D
考点:二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
解:二次函数 的大致图象如解图,
∵ ,且 ,
∴ , ,
①当 时,当 时,y取最小值,即 ,
解得 (舍去)或 ;
当 时,y取最大值,即 ,
解得 (舍去)或 (舍去);
②当 时,当 时y取最小值,即 ,
解得 (舍去)或 ;
当 时,y取最大值,即 ,
解得 ,
∴ .
故答案为:D.
分析:由 ,且 , 可得 , , 分两种情况①当 时,得出当 时,y取最小值,当 时,y取最大值;②当 时,得出当 时y取最小值当 时,y取最大值,据此分别解答即可.
4. A
考点:一元二次方程的根,一元二次方程根的判别式及应用,二次函数y=ax^2+bx+c的性质
解:由题意得:此方程的根的判别式 ,
解得 ,
是一元二次方程 的一个根,
,即 ,
对于任意实数m, 均成立,
令 ,
整理得: ,
由二次函数的性质可知,当 时,y取得最大值,最大值为 ,
即 的最大值等于 ,
故答案为:A.
分析:由 x=m是方程的根和一元二次方程根的判别式可得m,n的范围和 , 根据二次函数的性质可得最大值.
5. C
考点:二次函数的最值,二次函数y=ax^2+bx+c的性质
解: y=ax2+2ax+2a+5 ,
=a(x+1)2+a+5,
∵对称轴x=-1,?
∴ (﹣2,y1)离对称轴较近,(1,y2),离对称轴较远,
∵ y1??y2 ,
∴a<0,
当-2≤x≤1时,x=1取最小值,
即二次函数经过(1,-5),
∴-5=a+2a+2a+5,
∴a=-2.
故答案为:C.
分析:首先配方求出抛物线的对称轴方程,比较两点离对称轴的远近,结合其函数值的大小得出a<0,从而由函数的性质可知当x=1取最小值,把最小值代入函数式即可求出a值.
6. A
考点:二次函数的最值,二次函数图象与坐标轴的交点问题,二次函数y=ax^2+bx+c的性质
解:如图:
①∵(-1,0),(3,0)和(0,3)坐标都满足函数 ,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线 ,因此②也是正确的;
③根据函数的图象和性质,发现当 或 时,函数值y随x值的增大而增大,因此③也是正确的;
④函数图象的最低点就是与x轴的两个交点,根据y=0,求出相应的x的值为 或 ,因此④也是正确的;
⑤从图象上看,存在函数值要大于当 时的 ,因此⑤是不正确的.
故答案为:A.
分析:由y=0,建立关于x的方程,解方程求出x的值,就可得到图象与x轴的交点坐标,由x=0求出y的值,可得到图象与y轴的交点坐标,可对①作出判断;利用对称轴方程,可得到抛物线的对称轴,可对②作出判断;利用二次函数的性质,可得到函数值y随x值的增大而增大时自变量x的取值范围可对③作出判断;观察函数图象,利用函数解析式可求出函数的最小值为0时自变量x的值,可对④作出判断;由图象可知函数的最大值不能确定,可对⑤作出判断,综上所述可得到正确结论的个数.
7. C
考点:根据实际问题列二次函数关系式
解:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,
∵∠BAD=∠CAE=90°,即∠BAC+∠CAD=∠CAD+∠DAE
∴∠BAC=∠DAE
又∵AB=AD,∠ACB=∠E=90°
∴△ABC≌△ADE(AAS)
∴BC=DE,AC=AE,
设BC=a,则DE=a,DF=AE=AC=4BC=4a,
CF=AC﹣AF=AC﹣DE=3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2 , 即(3a)2+(4a)2=x2 ,
解得:a= ,
∴y=S四边形ABCD=S梯形ACDE= ×(DE+AC)×DF
= ×(a+4a)×4a
=10a2= x2 .
故答案为:C.
分析:作AE⊥AC,DE⊥AE,两线交于E点,作DF⊥AC垂足为F点,利用AAS判定△ABC和△ADE全等,然后利用全等三角形的性质得出BC=DE,AC=AE,设BC=a,则DE=a,DF=AE=AC=4BC=4a,CF=AC﹣AF=AC﹣DE=3a,利用勾股定理求出a与x的关系,分别用含x的代数式表示出DE、DF、AC,求出梯形AEDC的面积即为四边形ABCD的面积。
?8. B
考点:二次函数图象的几何变换,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的性质
解:∵ = ,
∴二次函数的顶点坐标为(1,-2),
∵点A坐标为 ,点B的坐标为 ,
∴二次函数图象是向左平移a个单位,再向上平移b个单位得到图象M,
∴平移后的顶点坐标为(1-a,-2+b)
∵图象M的顶点落在线段AB上,
∴-2≤1-a≤0,2≤-2+b≤3,
解得:1≤a≤3,4≤b≤5,
故答案为:B.
分析:先求出二次函数 = 的顶点坐标(1,-2),根据题意,二次函数图象是向左平移a个单位,再向上平移b个单位得到图象M,平移后的顶点坐标为(1-a,-2+b),进而得到满足条件的a、b的不等式,解之即可.
9. B
考点:二次函数图象与系数的关系,二次函数图象与坐标轴的交点问题,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的性质
解:①将(1,0)代入解析式,得 ,即a+b=-1,
故①符合题意;
②∵a<0
∴抛物线在对称轴左侧时,y随x的增大而增大
∵﹣2<x1<﹣1,另一交点为(1,0)
∴
∴当x=-1时,y>0,即
∴
故②符合题意;
③,由②得知 ,且a<0
∴ ,即
故③不符合题意;
④由根与系数的关系得到
∴
∴ ,解得﹣1<a<﹣
故④符合题意.
故答案为:B.
分析: 将(1,0)代入中,可得 , 据此判断①;由于a<0,可得抛物线在对称轴左侧时,y随x的增大而增大,由﹣2<x1<﹣1,另一交点为(1,0),可得 , 从而求出当x=-1时,y=? , 据此判断②;由且a<0,可得 , 据此判断③;由根与系数的关系得到 , 从而求出 , 即得 , 求出a的范围判断④即可.
10. C
考点:待定系数法求二次函数解析式,二次函数图象与坐标轴的交点问题,图形的旋转
解:当y=0时,﹣x(x﹣5)=0,解得x 1=0,x 2=5,则A 1(5,0),
∴OA1=5,
∵将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…;如此进行下去,得到一“波浪线”,
∴A1A2=A2A3=…=OA1=5,
∴抛物线C404的解析式为y=(x﹣5×403)(x﹣5×404),即y=(x﹣2015)(x﹣2020),
当x=2018时,y=(2018﹣2015)(2018﹣2020)=﹣6,
即m=﹣6.
故答案为:C
分析:先求出抛物线C1与x轴的交点坐标,观察图形可知第奇数个抛物线都在x轴上方,第偶数个抛物线都在x轴下方,2018÷5=403·····3,可判断点P在第404个抛物线上,用待定系数法先求出该抛物线的解析式,然后把点P的坐标代入计算即可得解.
11. C
考点:二次函数的最值,待定系数法求二次函数解析式
解:由题意知,函数p=at2+bt+c,
∴,
解得,
∴p=0.25t2+1.5t-1.7=-0.2(t-3.75)2+0.2×3.752-1.7
=-0.2(t-3.75)2+1.1125.
故当t=3.75时,p有最大值.
故答案为:C.
分析:利用待定系数法求出函数解析式,配方求出顶点坐标,即可得出加工煎炸臭豆腐的最佳时间.
12. A
考点:二次函数的实际应用-几何问题
解:C点移动到F点,重叠部分三角形的边长为x,由于是等边三角形,则高为 ,面积为y=x· · = ,
B点移动到F点,重叠部分三角形的边长为(4-x),高为 ,面积为
y=(4-x)· · = ,
两个三角形重合时面积正好为 .
由二次函数图象的性质可判断答案为A,
故答案为:A.
分析:根据图象可得出重叠部分三角形的边长为x,根据特殊角三角函数可得高为 ,由此得出面积y是x的二次函数,直到重合面积固定,再往右移动重叠部分的边长变为(4-x),同时可得
二、填空题
13. -2
考点:二次函数的定义
解:∵二次函数 (m为常数)的图象有最高点,
∴
解得:m=-2,
故答案为-2.
分析:根据二次函数的定义结合其有最高点确定m的值即可.
14.
考点:二次函数图象与几何变换
解:过点P作PM⊥y轴于点M,
∵抛物线平移后经过原点O和点A(﹣6,0),
∴平移后的抛物线对称轴为x=﹣3,
得出二次函数解析式为:y= (x+3)2+h,
将(﹣6,0)代入得出:
0= (﹣6+3)2+h,
解得:h=﹣ ,
∴点P的坐标是(﹣3,﹣ ),
根据抛物线的对称性可知,阴影部分的面积等于矩形NPMO的面积,
∴S=|﹣3|×|﹣ |= .
故答案为: .
分析:可转化阴影部分面积,进行分割,根据两抛物线形状相同,具有对称性,因此把x轴上侧的阴影面积补到下侧空白部分,构成完整的矩形.
15. - ≤a<0或0<a≤
考点:二次函数图象与系数的关系
解:将A、B两点代入抛物线,可得出b=-1,a+c=0,
所以抛物线为y=ax2-x-a(a≠0)
对称轴为
a<o,抛物线开口向下,对称轴<0
因为抛物线经过A、B
画图可得出当对称<0或≥1时,符合题意,a的趋势范围为
分析:将A、B两点代入,求得解析式,再根据对称轴进行判断。
16. 6和-19
考点:待定系数法求二次函数解析式,二次函数y=ax^2+bx+c的性质
解:二次函数y=-x2+mx+m=-(x- )2+ +m,
当4< 时,即m>8,
在-2≤x≤4时,x=4时取得最大值,则15=-42+4m+m,得m=6.2(舍去);
当 <-2时,即m<-4,
在-2≤x≤4时,x=-2时取得最大值,则15=-22-2m+m,得m=-19,
当-2≤ ≤4时,即-4≤m≤8,
在-2≤x≤4时,x= 时取得最大值,则15= +m,得m1=6,m2=-10(舍去),
由上可得,m的值是6和-19,
故答案为:6和-19.
分析:根据题目中的函数解析式和当-2≤x≤4时,y的最大值是15,利用分类讨论的方法可以求得m的值,本题得以解决.
17.
解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根
∴△=(-3)2-4×a×(-1)>0,
解得:a>?
设f(x)=ax2-3x-1,如图,
∵实数根都在-1和0之间,
∴-1<? <0,
∴a<? ,
且有f(-1)<0,f(0)<0,
即f(-1)=a×(-1)2-3×(-1)-1<0,f(0)=-1<0,
解得:a<-2,
∴? <a<-2,
故答案为:? <a<-2.
分析:首先根据根的情况利用判别式解得a的取值范围,然后根据已知中两个根的范围可知两个根的和大于-1且小于0,求出a的范围,画出草图可观察到x=1和x=0时ax2-3x-1的值都小于0,据此即可确定出a的范围.
18. 210
考点:待定系数法求二次函数解析式,探索数与式的规律,二次函数的其他应用
解:当一辆快递货车停靠在第x个服务驿站时,
快递货车上需要卸下已经通过的(x﹣1)个服务驿站发给该站的货包共(x﹣1)个,
还要装上下面行程中要停靠的(n﹣x)个服务驿站的货包共(n﹣x)个.
根据题意,完成下表:
服务驿站序号 在第x服务驿站启程时快递货车货包总数
1 n﹣1
2 (n﹣1)﹣1+(n﹣2)=2(n﹣2)
3 2(n﹣2)﹣2+(n﹣3)=3(n﹣3)
4 3(n﹣3)﹣3+(n﹣4)=4(n﹣4)
5 4(n﹣4)﹣4+(n﹣5)=5(n﹣5)
… …
n 0
由上表可得y=x(n﹣x).当n=29时,y=x(29﹣x)=﹣x2+29x=﹣(x﹣14.5)2+210.25,
当x=14或15时,y取得最大值210.
答:在整个行程中,快递货车装载的货包数量最多是210个.
故答案为:210.
分析:根据理解题意找出题目中所给的等量关系,找出规律,写出货包数量的函数解析式,再根据二次函数最值的求法求出快递货车装载的货包数量最多的站.
三、解答题
19. 解:∵抛物线的开口向下,∴a<0.∵ >0,∴b>0,∴2a-b<0.∵ =1,∴b+2a=0.当x=-1时,y=a-b+c<0,∴- b-b+c<0,∴3b-2c>0.∵抛物线与y轴的正半轴相交,∴c>0,∴3b+2c>0,∴P=3b-2c,Q=b-2a-3b-2c=-2a-2b-2c,∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-4b<0.∴P>Q.
考点:二次函数图象与系数的关系
分析:根据抛物线的开口向下得出a<0,由抛物线的对称轴在y轴的右侧,知a,b异号,根据抛物线的对称轴直线是1,得出b+2a=0,当x=-1时,y=a-b+c<0,故3b-2c>0,根据抛物线与y轴的正半轴相交,得出c>0,故3b+2c>0,然后根据绝对值的意义,去掉绝对值符号,再按整式加减的方法分别化简P,Q的值,再利用作差法,即可得出P,Q的大小。
20. 解:(Ⅰ)当a=b=1,c=﹣1时,抛物线为y=3x2+2x﹣1,方程3x2+2x﹣1=0的两个根为x1=﹣1, .∴该抛物线与x轴公共点的坐标是(﹣1,0)和( ,0);(Ⅱ)当a=b=1时,抛物线为y=3x2+2x+c,且与x轴有公共点.对于方程3x2+2x+c=0,判别式△=4﹣12c≥0,有c≤ .①当 时,由方程3x2+2x+ =0,解得x1=x2=﹣ .此时抛物线为y=3x2+2x+ 与x轴只有一个公共点(﹣ ,0);②当 时,x1=﹣1时,y1=3﹣2+c=1+c;x2=1时,y2=3+2+c=5+c.由已知﹣1<x<1时,该抛物线与x轴有且只有一个公共点,考虑其对称轴为 ,应有 即 ,解得﹣5<c≤﹣1.综上, 或﹣5<c≤﹣1.(6分)(Ⅲ)对于二次函数y=3ax2+2bx+c,由已知x1=0时,y1=c>0;x2=1时,y2=3a+2b+c>0,又∵a+b+c=0,∴3a+2b+c=(a+b+c)+2a+b=2a+b.∴2a+b>0.∵b=﹣a﹣c,∴2a﹣a﹣c>0,即a﹣c>0.∴a>c>0.(7分)∵关于x的一元二次方程3ax2+2bx+c=0的判别式△=4b2﹣12ac=4(a+c)2﹣12ac=4[(a﹣c)2+ac]>0,∴抛物线y=3ax2+2bx+c与x轴有两个公共点,顶点在x轴下方.又该抛物线的对称轴 ,由a+b+c=0,c>0,2a+b>0,得﹣2a<b<﹣a,∴ .又由已知x1=0时,y1>0;x2=1时,y2>0,观察图象,
可知在0<x<1范围内,该抛物线与x轴有两个公共点.
考点:二次函数图象与坐标轴的交点问题
分析:(Ⅰ)把a,b,c的值代入可得抛物线的解析式,然后令y=0可得到关于x的方程,然后求得方程的两根,从而可得到抛物线与x轴交点坐标;
(Ⅱ)把a,b代入可得到抛物线的解析式,然后可求得抛物线的对称轴为x=- , 然后再分为△=0和△>0两种情况求解即可;
(Ⅲ)抛物线y=3ax2+2bx+c与x轴公共点的个数就是一元二次方程3ax2+2bx+c=0的实数根的个数,接下来,判断出方程3ax2+2bx+c=0根的判别式的符号,依据判别式的符号得出相应的结论.
21. (1)解:如图
将图9中的抛物线 向下平移2个单位长,可得抛物线
画法:①列表;②描点(五点画图法);③用光滑的曲线连接这五个点.
(2)解:由题意,得点 的“关联点”为
由点 在抛物线 上,可得 ,
又∵ 在抛物线 上,∴
解得 .将 代入 ,得
(3)解:点 的“待定关联点”为 ,
∵ 在抛物线 的图像上,∴ .
∴ , .又∵ ,∴ .
?当 时, ,故可得
考点:二次函数图象的几何变换,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的图象
分析:(1)利用图像的平移规律,将 向下平移2个单位长度即可得到 (2)先根据题意求出 ,再代入到 中,联合A代入到 即可求出答案.(3)将 代入 中解出x的值,可点 的坐标即可用含n的代数式表示.
22. (1)解: 函数的图象与x轴相交于O,.
,
二次函数的解析式为y=x-3x.
(2)解:假设存在点 ,过点 作 轴于点 , 的面积等于6,。
.
当 时, ,解得 或3
, ,即 ,解得 或 (舍去).
又 顶点坐标为 , , ? 下方不存在 点.
点 的坐标为
(3)解: 点 的坐标为 , , ?当 时, .
设P点横坐标为 ,则纵坐标为 ,即 ,解得 或 .
在抛物线上仅存在一点
的面积为:
考点:二次函数y=ax^2+bx+c的图象,二次函数y=ax^2+bx+c的性质
分析:(1)将原点的坐标代入抛物线,即可得到k的值;
(2)根据得到的抛物线的解析式求出点A的坐标,即可得到OA的长度,根据△OAB的面积求出B点纵坐标的绝对值,代入抛物线中,计算得到点B的坐标即可;
(3)根据点B的坐标计算直线OB的解析式,求出点P的坐标特点,代入解析式计算得到坐标即可。计算△POB的面积,求出OB和OP的长度,即可得到答案。
23. (1)解:将点A(-1,0)、B(3,0)代入抛物线解析式y=ax2-2x+c可得:
,解得: ,
∴抛物线的解析式为y=x2-2x-3,
当x=0时,y=-3,所以C的坐标为C(0,-3)
(2)解:∵B(3,0),C(0,-3),可得直线BC解析式为:y=x-3,
设与直线BC平行且在BC下方的一条直线l解析式为y=x+b,当直线l与抛物线只有一个交点时,△PBC的面积最大,
联立解析式 ,
可得 ,
整理得: ,
∴ ,解得:b= ,
即 ,解得:x= ,将x= 代入抛物线解析式可得 ,
所以P ,
如图1,过点P作PM⊥y轴于M,∴M(0, ),
∴
∴△PBC的最大面积为
(3) 或 或 .
考点:待定系数法求二次函数解析式,翻折变换(折叠问题),相似三角形的判定与性质,二次函数图象上点的坐标特征,二次函数y=ax^2+bx+c的性质
解:(3)根据(1)中解析式可得:D(1,-4),直线x=1交x轴于F,BD= ,
分类讨论:
①如图3,EQ⊥DB于Q,△DEQ沿边EQ翻折得到△D’EQ,
∵∠EDQ=∠BDF,
∴Rt△DEQ∽Rt△DBF,
∴ ,即 ,
解得DQ= ,
∴BQ=BD?DQ=
②如图4, ED′⊥BD于H,
∵∠EDH=∠BDF,
∴Rt△DEH∽Rt△DBF,
∴ ,即 ,
解得DH= ,EH= ,
在Rt△QHD′中,设QH=x,D′Q=DQ=DH?HQ=
, D′H=D′E?EH=DE?EH=2? ,
∴ ,解得x=1? ,
∴BQ=BD?DQ=BD?(DH?HQ)=BD?DH+HQ= ,;
③如图5,D′Q⊥BC于G,作EI⊥BD于I,易得EI= ,BI= ,
∵△DEQ沿边EQ翻折得到△D′EQ,
∴∠EQD=∠EQD′,
∴EG=EI= ,
∵BE= ,
∴BG=BE?EG=
∵∠GBQ=∠IBE,
∴△BQG∽△BEI,
∴ ,即
∴BQ=
综上所述,当BQ为 或 或 时,将△DEQ沿边EQ翻折得到△D′EQ,使得△D′EQ与△BEQ的重叠部分图形为直角三角形.
?
分析:(1)将点A(-1,0)、B(3,0)代入抛物线解析式可求出a,c的值,得到抛物线的解析式,令x=0可求出c的坐标;(2)直线BC解析式为:y=x-3,设与直线BC平行且在BC下方的一条直线l解析式为y=x+b,当直线l与抛物线只有一个交点时,△PBC的面积最大,联立解析式,求出当 时x的值,即为P点横坐标,再根据分割面积法求出此时 ;(3)根据(1)中解析式可得:D(1,-4),直线x=1交x轴于F,BD= ,然后分情况讨论,分别求出BQ的长即可.]
24. (1)证明:因为二次函数y= (a+c)x2-bx+ (c-a)的顶点在x轴上,
∴Δ=0,即:b2-4× (a+c)× (c-a)=0,
∴c2=a2+b2 ,
得∠ACB=90°.
(2)解:∵z2+z-20=0.
∴z1=-5,z2=4,
∵a>0,得a=4.
设b=AC=2x,有S△ABC= AC·BC=4x,S半圆= p ?x2
∴S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆=- x2+4x
(3)解: S2-S1=- (x- )2+ ,
∴当x= 时,(S2-S1)有最大值 .
这时,b= ,a=4,c= ,
如图,连接
为圆的直径,
?
?
?
?
?BD= .
当BD为 时,(S2-S1)最大.
考点:根据实际问题列二次函数关系式,相似三角形的判定与性质,利用二次函数图象判断一元二次方程根的情况
分析:(1)由抛物线的顶点在x轴上,得到 从而可得结论.(2)利用a是z2+z-20=0的根,求解 的值,再利用S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆 , 从而可得答案,(3)由(2)的函数关系式求解( )最大时 ,利用直径所对的圆周角是直角,得到 利用相似三角形的性质可得答案.
25. (1)x-3,2x-3
(2)解:由题意得:
y=200(x-3)2+100× x2×2+150× ×3×(2x-3)×2
=200(x-3)2+100x2+450(2x-3)
=300x2-300x+450,
∴y=300x2-300x+450(x>3)
(3)解:由题意得:2x-3≥3+4,
解得:x≥5,
∵y=300x2-300x+450(x>3);
∴y=300(x- )2+375
∵a=300>0,对称轴为直线x= ,
∴当x> 时,y随着x的增大而增大,
又∵x≥5,
∴当x=5时,y取得最小值,最小值为6450,
答:总费用y的最小值为6450元.
考点:二次函数的实际应用-几何问题
解:(1)∵ ABH和 CDF是全等的直角三角形,AH=3米,
∴CF=AH=3米,
∵ AGD和 BEC是全等的等腰直角三角形,BE=x米,
∴AG=GD=EC=BE=x米,
∴EF=EC-CF=x-3,
∵四边形EFGH是正方形,
∴FG=EF=x-3,
∴FD=FG+GD
=x-3+x
=2x-3,
故答案为:x-3,2x-3;
分析:(1)由题意可得CF=AH=3米,AG=GD=EC=BE=x米,由此可得EF=EC-CF=x-3,再由正方形EFGH可得FG=EF=x-3,由此即可表示出FD的长;(2)根据总费用等于各部分的费用之和即可列出y关于x的函数解析式;(3)由2x-3≥3+4可得x≥5,由y=300x2-300x+450可得y=300(x- )2+375,再根据二次函数的增减性即可求得x≥5的y的最小值.
26. (1)解:根据表格中的数据可知,发射14分时到达轨道的远地点,此时距离地面的高度为1000千米.
(2)解:根据表中数据可知第二阶段的曲线为抛物线,
可设抛物线为 ,将点 代入,
∴ ,
解得: ,
∴抛物线的解析式为: ,
当 ,1,2,4,5时, 依次为 , ,136,400,514.
∴ .
∴导弹在第5分钟开始进入飞行第二阶段;
(3)解:令 ,则 ,
解得: , (不合题意,舍去).
答:导弹发射 分钟熄火.
考点:二次函数的其他应用
分析:(1)根据表格的数据,即可得到答案;
(2)结合表格中的数据,设函数解析式为 ,利用待定系数法进行解题,即可求出答案;
(3)令 ,代入函数解析式,即可求出答案.
_21?????????è?????(www.21cnjy.com)_
