四川省成都新津区高级中学校2020-2021学年高二下学期入学考试数学(文)试题 Word版含答案
文档属性
| 名称 | 四川省成都新津区高级中学校2020-2021学年高二下学期入学考试数学(文)试题 Word版含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 262.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览




文档简介
新津中学高2019级(高二)下期入学考试
数学(文科)
一、选择题
1.已知一组数据为-3,5,7,x,11,且这组数据的众数为5,那么该组数据的中位数是( )
A.11 B.5 C.6 D.7
2.双曲线C:-=1(a>0,b>0)的一条渐近线的倾斜角为130°,则C的离心率为( )
A.2sin 40° B.2cos 40° C. D.
3.三角形的三个顶点A(2, -1, 4), B(3, 2, -6), C(5, 0, 2), 则过A点的中线长为 ( )
A. B.2 C.11 D.3
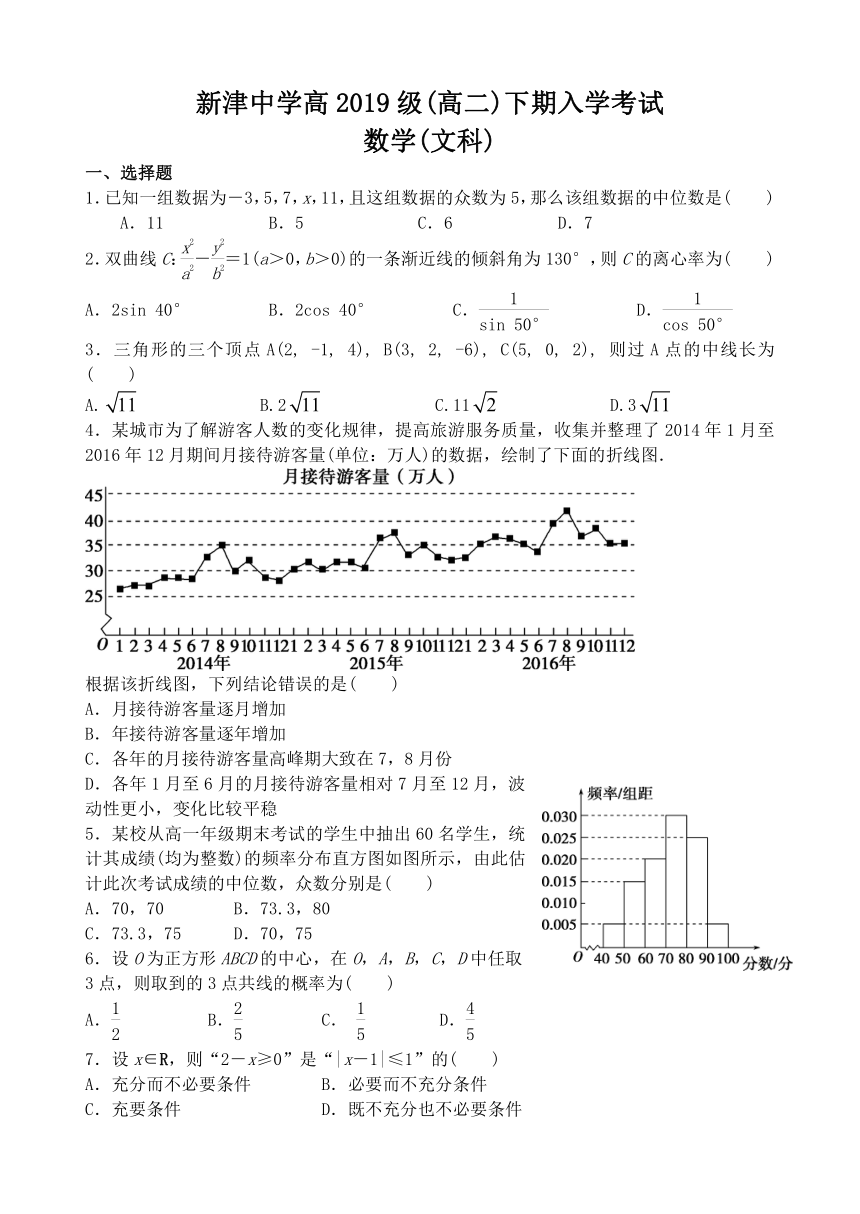
4.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月份
D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳
5.某校从高一年级期末考试的学生中抽出60名学生,统计其成绩(均为整数)的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数分别是( )
A.70,70 B.73.3,80
C.73.3,75 D.70,75
6.设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
A. B. C. D.
7.设x∈R,则“2-x≥0”是“|x-1|≤1”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
8.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在直线x+y=4上的概率是( )
A. B. C. D.
9.从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图如图.根据茎叶图,下列描述正确的是( )
A.甲种树苗的平均高度大于乙种树苗的平均高度,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的平均高度大于乙种树苗的平均高度,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的平均高度大于甲种树苗的平均高度,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的平均高度大于甲种树苗的平均高度,但甲种树苗比乙种树苗长得整齐
10.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,|AB|=43,则C的实轴长为( )
A.2 B.22 C.4 D.8
11.圆关于直线对称的圆的方程是( )
A. B.
C. D.
12.已知点分别是双曲线的左右两焦点,过点的直线与双曲线的左右两支分别交于两点,若是以 为顶角的等腰三角形,其中,则双曲线离心率的取值范围为( )
A. B. C. D.
二、填空题
13.从甲、乙、丙三个厂家生产的同一种产品中抽取8件产品,对其使用寿命(单位:年)进行追踪调查的结果如下:
甲:3,4,5,6,8,8,8,10;
乙:4,6,6,6,8,9,12,13;
丙:3,3,4,7,9,10,11,12.
三个厂家广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别运用了平均数,众数,中位数中的哪一种集中趋势的特征数.
甲:________,乙:________,丙:________.
14.已知直线l:x-3y-a=0与圆C:(x-3)2+(y+3)2=4交于M,N,点P在圆C上,且∠MPN=π/3,则实数a= .
15.任意说出星期一到星期日中的两天(不重复),其中恰有一天是星期六的概率是_______
16.已知双曲线的左、右焦点分别为F1,F2,实轴长为1,P是双曲线右支上的一点,满足|PF1|=3,M是y轴上的一点,则 .
三、解答题
17.已知双曲线中心在原点,以坐标轴为对称轴,且与圆x2+y2=17相交于A(4,-1).若圆在A点处的切线与双曲线的渐近线平行,求此双曲线方程.
18.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
19.已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若·=12,其中O为坐标原点,求|MN|.
20.以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
房屋面积(m2) 115 110 80 135 105
销售价格(万元) 24.8 21.6 18.4 29.2 22
(1)画出数据对应的散点图;
(2)求回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150 m2时的销售价格.
21.已知A,B分别为椭圆E:+y2=1(a>1)的左、右顶点,G为E的上顶点,·=8.P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
(2)证明:直线CD过定点.
22.已知椭圆C:+=1(a>b>0),e=,其中F是椭圆的右焦点,焦距为2,直线l与椭圆C交于点A,B,线段AB的中点横坐标为,且=λ(其中λ>1).
(1)求椭圆C的标准方程;
(2)求实数λ的值.
新津中学高2019级(高二)下期入学考试
参考答案
一、选择题:
BDBAC CBDDC CA
二、填空题
13.甲:众数,乙:平均数,丙:中位数;
14. a=12; 15.; 16.(文) (理)
三、解答题
17. 答案:x2-y2=1
18. 答案:(1)由已知得0.70=a+0.20+0.15,故
a=0.35.
b=1-0.05-0.15-0.70=0.10.
(2)甲离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
19.答案: (1)由题设可知直线l的方程为y=kx+1.
因为直线l与圆C交于两点,所以<1,
解得所以k的取值范围为.
(2)设M(x1,y1),N(x2,y2).
将y=kx+1代入方程(x-2)2+(y-3)2=1,
整理得(1+k2)x2-4(1+k)x+7=0.
所以x1+x2=,x1x2=.
·=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1
=+8.
由题设可得+8=12,解得k=1,
所以直线l的方程为y=x+1.
故圆心C在直线l上,所以|MN|=2.
20. 答案:(1)数据对应的散点图如图所示:
(2)=0.196 2x+1.814 2,回归直线如图中线所示.
(3)31.244 2(万元).
21.答案:(1)由题设得A(-a,0),B(a,0),G(0,1).
则=(a,1),=(a,-1).由·=8
得a2-1=8,即a=3.
所以E的方程为+y2=1.
(2)设C(x1,y1),D(x2,y2),P(6,t).
若t≠0,设直线CD的方程为x=my+n,由题意可知-3由于直线PA的方程为y=(x+3),
所以y1=(x1+3).
直线PB的方程为y=(x-3),
所以y2=(x2-3).
可得3y1(x2-3)=y2(x1+3).
由于,9)+y=1,故y=-,
可得27y1y2=-(x1+3)(x2+3),
即(27+m2)y1y2+m(n+3)(y1+y2)+(n+3)2=0.①
将x=my+n代入+y2=1得(m2+9)y2+2mny+n2-9=0.
所以y1+y2=-,y1y2=.
代入①式得(27+m2)(n2-9)-2m(n+3)mn+(n+3)2·(m2+9)=0.
解得n=-3(含去),n=.
故直线CD的方程为x=my+,
即直线CD过定点(,0).
若t=0,则直线CD的方程为y=0,过点(,0).
综上,直线CD过定点(,0).
22(文)答案:(1)由椭圆的焦距为2,知c=1,
又e=,∴a=2,故b2=a2-c2=3,
∴椭圆C的标准方程为+=1.
(2)由=λ,可知A,B,F三点共线,
设点A(x1,y1),点B(x2,y2).
若直线AB⊥x轴,
则x1=x2=1,不符合题意;
当AB所在直线l的斜率k存在时,
设l的方程为y=k(x-1).
由消去y得
(3+4k2)x2-8k2x+4k2-12=0.①
①的判别式Δ=64k4-4(4k2+3)(4k2-12)=144(k2+1)>0,
∴
∴x1+x2==2×=,
∴k2=.
将k2=代入方程①,
得4x2-2x-11=0,
解得x=.
又=(1-x1,-y1),
=(x2-1,y2),=λ,
即1-x1=λ(x2-1),λ=,
又λ>1,∴λ=.
22(理) 答案:(1)由已知椭圆的焦点在x轴上,设其方程为+=1(a>b>0),则A(a,0),B(0,b),F(c,0)(c=).
由已知可得e2==,所以a2=4b2,
即a=2b,c=b①
S△ABF=×|AF|×|OB|=(a-c)b=1-.②
将①代入②,得(2b-b)b=1-,解得b=1,故a=2,c=.
所以椭圆C的方程为+y2=1.
(2)圆O的圆心为坐标原点(0,0),半径r=1,由直线l:y=kx+m与圆O:x2+y2=1相切,得=1,故有m2=1+k2.③
由消去y,
得(1+4k2)x2+8kmx+4(m2-1)=0,由题可知k≠0,
所以Δ=16(4k2-m2+1)=48k2>0.
设M(x1,y1),N(x2,y2),则x1+x2=,x1x2=.
所以|x1-x2|2=(x1+x2)2-4x1x2=2-4×=.④
将③代入④中,得|x1-x2|2=,
故|x1-x2|=.
所以|MN|=|x1-x2|=×=.
故△OMN的面积S=|MN|×1=××1=.
令t=4k2+1,则t≥1,k2=,代入上式,得
S=2=
==
==,
所以当t=3,即4k2+1=3,解得k=±时,S取得最大值,且最大值为×=1.
数学(文科)
一、选择题
1.已知一组数据为-3,5,7,x,11,且这组数据的众数为5,那么该组数据的中位数是( )
A.11 B.5 C.6 D.7
2.双曲线C:-=1(a>0,b>0)的一条渐近线的倾斜角为130°,则C的离心率为( )
A.2sin 40° B.2cos 40° C. D.
3.三角形的三个顶点A(2, -1, 4), B(3, 2, -6), C(5, 0, 2), 则过A点的中线长为 ( )
A. B.2 C.11 D.3
4.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月份
D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳
5.某校从高一年级期末考试的学生中抽出60名学生,统计其成绩(均为整数)的频率分布直方图如图所示,由此估计此次考试成绩的中位数,众数分别是( )
A.70,70 B.73.3,80
C.73.3,75 D.70,75
6.设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
A. B. C. D.
7.设x∈R,则“2-x≥0”是“|x-1|≤1”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
8.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在直线x+y=4上的概率是( )
A. B. C. D.
9.从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图如图.根据茎叶图,下列描述正确的是( )
A.甲种树苗的平均高度大于乙种树苗的平均高度,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的平均高度大于乙种树苗的平均高度,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的平均高度大于甲种树苗的平均高度,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的平均高度大于甲种树苗的平均高度,但甲种树苗比乙种树苗长得整齐
10.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,|AB|=43,则C的实轴长为( )
A.2 B.22 C.4 D.8
11.圆关于直线对称的圆的方程是( )
A. B.
C. D.
12.已知点分别是双曲线的左右两焦点,过点的直线与双曲线的左右两支分别交于两点,若是以 为顶角的等腰三角形,其中,则双曲线离心率的取值范围为( )
A. B. C. D.
二、填空题
13.从甲、乙、丙三个厂家生产的同一种产品中抽取8件产品,对其使用寿命(单位:年)进行追踪调查的结果如下:
甲:3,4,5,6,8,8,8,10;
乙:4,6,6,6,8,9,12,13;
丙:3,3,4,7,9,10,11,12.
三个厂家广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别运用了平均数,众数,中位数中的哪一种集中趋势的特征数.
甲:________,乙:________,丙:________.
14.已知直线l:x-3y-a=0与圆C:(x-3)2+(y+3)2=4交于M,N,点P在圆C上,且∠MPN=π/3,则实数a= .
15.任意说出星期一到星期日中的两天(不重复),其中恰有一天是星期六的概率是_______
16.已知双曲线的左、右焦点分别为F1,F2,实轴长为1,P是双曲线右支上的一点,满足|PF1|=3,M是y轴上的一点,则 .
三、解答题
17.已知双曲线中心在原点,以坐标轴为对称轴,且与圆x2+y2=17相交于A(4,-1).若圆在A点处的切线与双曲线的渐近线平行,求此双曲线方程.
18.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成A,B两组,每组100只,其中A组小鼠给服甲离子溶液,B组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到P(C)的估计值为0.70.
(1)求乙离子残留百分比直方图中a,b的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
19.已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若·=12,其中O为坐标原点,求|MN|.
20.以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
房屋面积(m2) 115 110 80 135 105
销售价格(万元) 24.8 21.6 18.4 29.2 22
(1)画出数据对应的散点图;
(2)求回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150 m2时的销售价格.
21.已知A,B分别为椭圆E:+y2=1(a>1)的左、右顶点,G为E的上顶点,·=8.P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
(1)求E的方程;
(2)证明:直线CD过定点.
22.已知椭圆C:+=1(a>b>0),e=,其中F是椭圆的右焦点,焦距为2,直线l与椭圆C交于点A,B,线段AB的中点横坐标为,且=λ(其中λ>1).
(1)求椭圆C的标准方程;
(2)求实数λ的值.
新津中学高2019级(高二)下期入学考试
参考答案
一、选择题:
BDBAC CBDDC CA
二、填空题
13.甲:众数,乙:平均数,丙:中位数;
14. a=12; 15.; 16.(文) (理)
三、解答题
17. 答案:x2-y2=1
18. 答案:(1)由已知得0.70=a+0.20+0.15,故
a=0.35.
b=1-0.05-0.15-0.70=0.10.
(2)甲离子残留百分比的平均值的估计值为
2×0.15+3×0.20+4×0.30+5×0.20+6×0.10+7×0.05=4.05.
乙离子残留百分比的平均值的估计值为
3×0.05+4×0.10+5×0.15+6×0.35+7×0.20+8×0.15=6.00.
19.答案: (1)由题设可知直线l的方程为y=kx+1.
因为直线l与圆C交于两点,所以<1,
解得
(2)设M(x1,y1),N(x2,y2).
将y=kx+1代入方程(x-2)2+(y-3)2=1,
整理得(1+k2)x2-4(1+k)x+7=0.
所以x1+x2=,x1x2=.
·=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1
=+8.
由题设可得+8=12,解得k=1,
所以直线l的方程为y=x+1.
故圆心C在直线l上,所以|MN|=2.
20. 答案:(1)数据对应的散点图如图所示:
(2)=0.196 2x+1.814 2,回归直线如图中线所示.
(3)31.244 2(万元).
21.答案:(1)由题设得A(-a,0),B(a,0),G(0,1).
则=(a,1),=(a,-1).由·=8
得a2-1=8,即a=3.
所以E的方程为+y2=1.
(2)设C(x1,y1),D(x2,y2),P(6,t).
若t≠0,设直线CD的方程为x=my+n,由题意可知-3
所以y1=(x1+3).
直线PB的方程为y=(x-3),
所以y2=(x2-3).
可得3y1(x2-3)=y2(x1+3).
由于,9)+y=1,故y=-,
可得27y1y2=-(x1+3)(x2+3),
即(27+m2)y1y2+m(n+3)(y1+y2)+(n+3)2=0.①
将x=my+n代入+y2=1得(m2+9)y2+2mny+n2-9=0.
所以y1+y2=-,y1y2=.
代入①式得(27+m2)(n2-9)-2m(n+3)mn+(n+3)2·(m2+9)=0.
解得n=-3(含去),n=.
故直线CD的方程为x=my+,
即直线CD过定点(,0).
若t=0,则直线CD的方程为y=0,过点(,0).
综上,直线CD过定点(,0).
22(文)答案:(1)由椭圆的焦距为2,知c=1,
又e=,∴a=2,故b2=a2-c2=3,
∴椭圆C的标准方程为+=1.
(2)由=λ,可知A,B,F三点共线,
设点A(x1,y1),点B(x2,y2).
若直线AB⊥x轴,
则x1=x2=1,不符合题意;
当AB所在直线l的斜率k存在时,
设l的方程为y=k(x-1).
由消去y得
(3+4k2)x2-8k2x+4k2-12=0.①
①的判别式Δ=64k4-4(4k2+3)(4k2-12)=144(k2+1)>0,
∴
∴x1+x2==2×=,
∴k2=.
将k2=代入方程①,
得4x2-2x-11=0,
解得x=.
又=(1-x1,-y1),
=(x2-1,y2),=λ,
即1-x1=λ(x2-1),λ=,
又λ>1,∴λ=.
22(理) 答案:(1)由已知椭圆的焦点在x轴上,设其方程为+=1(a>b>0),则A(a,0),B(0,b),F(c,0)(c=).
由已知可得e2==,所以a2=4b2,
即a=2b,c=b①
S△ABF=×|AF|×|OB|=(a-c)b=1-.②
将①代入②,得(2b-b)b=1-,解得b=1,故a=2,c=.
所以椭圆C的方程为+y2=1.
(2)圆O的圆心为坐标原点(0,0),半径r=1,由直线l:y=kx+m与圆O:x2+y2=1相切,得=1,故有m2=1+k2.③
由消去y,
得(1+4k2)x2+8kmx+4(m2-1)=0,由题可知k≠0,
所以Δ=16(4k2-m2+1)=48k2>0.
设M(x1,y1),N(x2,y2),则x1+x2=,x1x2=.
所以|x1-x2|2=(x1+x2)2-4x1x2=2-4×=.④
将③代入④中,得|x1-x2|2=,
故|x1-x2|=.
所以|MN|=|x1-x2|=×=.
故△OMN的面积S=|MN|×1=××1=.
令t=4k2+1,则t≥1,k2=,代入上式,得
S=2=
==
==,
所以当t=3,即4k2+1=3,解得k=±时,S取得最大值,且最大值为×=1.
同课章节目录
