高中物理选修3-4 11.3 简谐运动的回复力和能量(共29张PPT)
文档属性
| 名称 | 高中物理选修3-4 11.3 简谐运动的回复力和能量(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-09 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
1、描述简谐运动的物理量
振幅:描述振动强弱;
周期和频率:描述振动快慢;
相位:描述振动步调.
2、简谐运动的表达式:
复习回顾
第三节
简谐运动的回复力和能量
回复力:振动物体偏离平衡位置后,所受到的使它回到平衡位置的力。
一.简谐运动的回复力
1.定义:
2.特点:
方向始终指向平衡位置,按力的作用效果命名
使振子回到平衡位置的力
3.来源:
振动方向上的合外力
如果质点所受的回复力与它偏离平衡位置的位移大小成正比,方向相反(始终指向平衡位置),质点的运动就是简谐运动。
5.简谐运动的动力学特点(条件):
6.简谐运动的运动学特点:
4.公式:
一.简谐运动的回复力
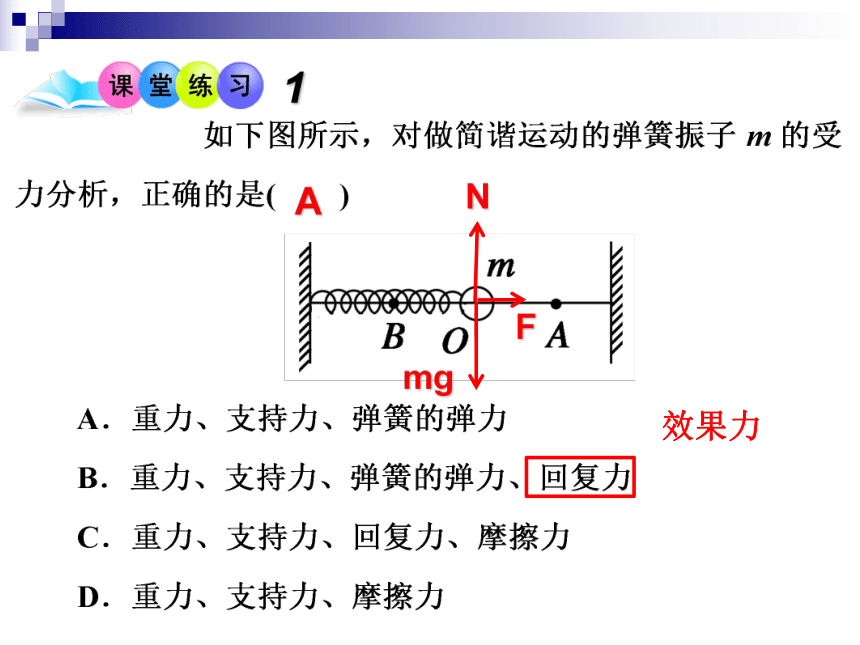
A
1
N
mg
F
效果力
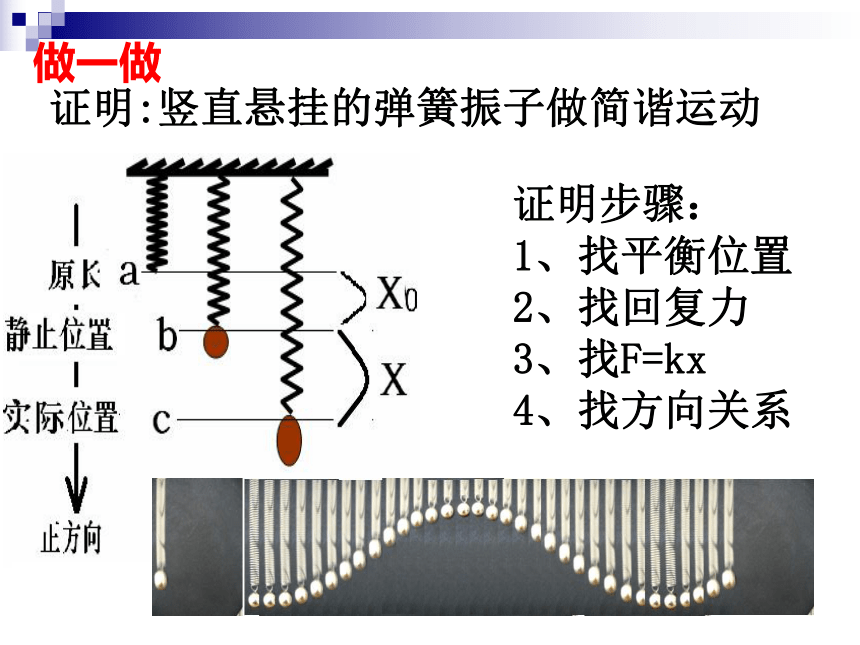
证明:竖直悬挂的弹簧振子做简谐运动
证明步骤:
1、找平衡位置
2、找回复力
3、找F=kx
4、找方向关系
做一做
证明:竖直悬挂的弹簧振子做简谐运动
做一做
证明:平衡状态时有:
当向下拉动x长度时弹簧所受的合外力为
KX0
mg
mg
K(X+X0)
F
振动方向上合力F与位移X方向相反,故
F=
-
kx成立,该振动为简谐运动
O
A
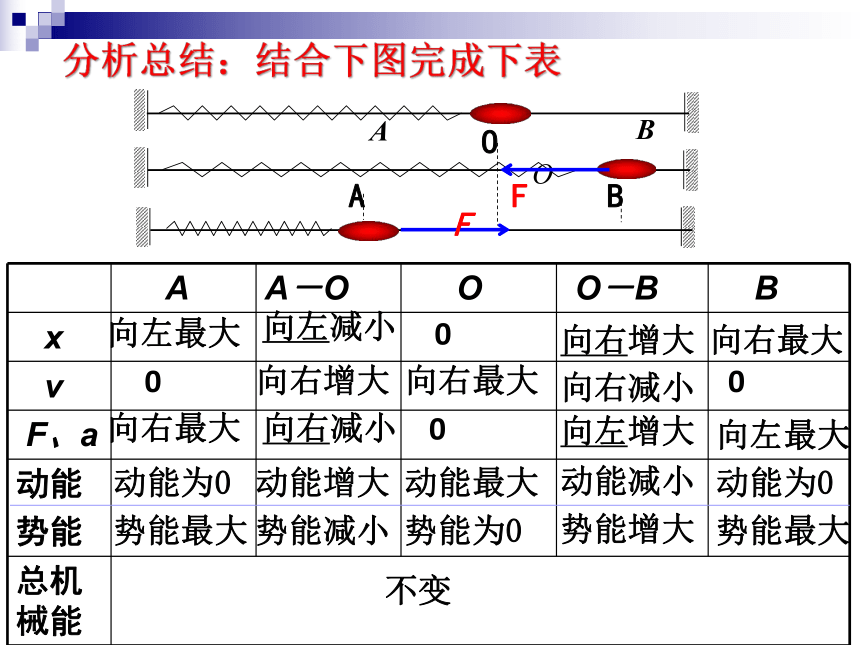
A
A-O
O
O-B
B
x
v
F、a
动能
势能
总机械能
向左减小
向右增大
向右减小
动能增大
势能减小
B
向右增大
向右减小
向左增大
动能减小
势能增大
不变
向左最大
向右最大
0
0
向右最大
0
0
向右最大
向左最大
动能最大
势能为0
动能为0
势能最大
动能为0
势能最大
O
B
A
F
F
分析总结:结合下图完成下表
A
B
O
位移:Xm
X=0
Xm
回复力:Fm
F=0
Fm
加速度:am
a=0
am
势能:Epm
Ep=0
Epm
总机械能:
E
E
E
动能:Ek=
0
Ekm
Ek=
0
速度:V=0
Vm
V=0
D
2
A
B
O
X↓
F↓
a↓
V↑
→
→
→
.简谐运动的特点:
1、回复力与位移成正比而方向相反,总是指向平衡位置。
2、简谐运动是一种理想化的运动,振动过程中无阻力,所以振动系统机械能守恒。
3、简谐运动是一种非匀变速运动。
4、具有往复性,对称性、周期性
简谐振动中的对称关系
(1)关于平衡位置的
对称点
①a、F、X大小相同,方向相反;动能势能相同
②V大小相同,方向不一定
(2)先后通过同一位置
①a、F、X,动能势能相同
②V大小相同,方向相反
ABD
3
X大小相同
→
EP相同
→
Ek相同
A
B
O
a
b
振子连续两次通过P位置,下列各量哪些是相同的?
位移(
)
回复力(
)
加速度(
)
动能(
)
势能(
)
速率(
)
速度(
)
动量(
)
√
×
√
√
√
√
√
×
O
B
A
P
x
简谐运动中动能和势能在发生相互转化,但机械能的总量保持不变,即机械能守恒。
试画出物体在做简谐运动时的Ek-t和Ep-t及E-t图象
t
E
0
机械能
势能
动能
A
B
O
简谐运动的能量由劲度系数和振幅决定.
二.简谐运动的能量
从平衡位置开始计时,取向右为正方向
三.简谐运动中各个物理量的变化规律
4
5
AD
C
小结
1、回复力:使振动物体回到平衡位置的力.
2、简谐运动回复力的特点:如果质点所受的回复力与它偏离平衡位置的位移大小成正比,方向相反,(始终指向平衡位置),质点的运动就是简谐运动。
3、简谐运动中动能和势能在发生相互转化,但机械能的总量保持不变,即机械能守恒.
O
分析:
沿振动方向有两个力,弹簧的弹力和重力的分力,二者的合力提供回复力
设平衡时弹簧的伸长量为x0,则有
此时回复力为零,该位置为平衡位置记为O。
若拉长x,则弹力为F∕=k(x0+x)
此时回复力F=F∕-mgsinθ=kx,而F方向与x方向相反。
故
F=
-
kx成立
该振动为简谐运动
x
mgsinθ
F∕
课本第12页第一题
BC
6
A
B
O
BC
7
A
B
O
ABC
8
B处速度为0
放m上时无能量损失
↑
↑
?若在o点轻放m则应选(
)
BD
D
9
a=0
g
↓
↑
g
V
V
V=0
a>g
Vm
向下压缩弹簧
KX
mg
对称性
10
C
整体:kA=(3m/2)am
对于m/2:Ff=(m/2)am
11
AC
A
A-O
O
O-B
B
x
v
F、a
动能
势能
总机械能
向左减小
向右增大
向右减小
动能增大
势能减小
向右增大
向右减小
向左增大
动能减小
势能增大
不变
向左最大
向右最大
0
0
向右最大
0
0
向右最大
向左最大
动能最大
势能为0
动能为0
势能最大
动能为0
势能最大
判断物体是否做简谐运动的方法:
(1)根据物体的振动图像去判断
(2)根据回复力的规律F=-kx去判断
思考:
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
【思考题】
判断物体是否做简谐运动的方法:
(2)根据回复力的规律F=-kx去判断
(1)根据物体的振动图像去判断
证明:竖直悬挂的弹簧振子做简谐运动
①找平衡位置
在平衡位置处
②找回复力
指向平衡位置的合力
将小球拉离平衡位置到c点,
此时偏离平衡位置的位移为x,方向向下
方向向上
③找F=kx
x偏离平衡位置的位移
④找方向关系
证明:平衡状态时有:
mg=-kx0
当向下拉动x长度时弹簧所受的合外力为
F=-k(x+x0)+mg
=-kx-kx0+mg
=-kx
(符合简谐运动的公式)
1、描述简谐运动的物理量
振幅:描述振动强弱;
周期和频率:描述振动快慢;
相位:描述振动步调.
2、简谐运动的表达式:
复习回顾
第三节
简谐运动的回复力和能量
回复力:振动物体偏离平衡位置后,所受到的使它回到平衡位置的力。
一.简谐运动的回复力
1.定义:
2.特点:
方向始终指向平衡位置,按力的作用效果命名
使振子回到平衡位置的力
3.来源:
振动方向上的合外力
如果质点所受的回复力与它偏离平衡位置的位移大小成正比,方向相反(始终指向平衡位置),质点的运动就是简谐运动。
5.简谐运动的动力学特点(条件):
6.简谐运动的运动学特点:
4.公式:
一.简谐运动的回复力
A
1
N
mg
F
效果力
证明:竖直悬挂的弹簧振子做简谐运动
证明步骤:
1、找平衡位置
2、找回复力
3、找F=kx
4、找方向关系
做一做
证明:竖直悬挂的弹簧振子做简谐运动
做一做
证明:平衡状态时有:
当向下拉动x长度时弹簧所受的合外力为
KX0
mg
mg
K(X+X0)
F
振动方向上合力F与位移X方向相反,故
F=
-
kx成立,该振动为简谐运动
O
A
A
A-O
O
O-B
B
x
v
F、a
动能
势能
总机械能
向左减小
向右增大
向右减小
动能增大
势能减小
B
向右增大
向右减小
向左增大
动能减小
势能增大
不变
向左最大
向右最大
0
0
向右最大
0
0
向右最大
向左最大
动能最大
势能为0
动能为0
势能最大
动能为0
势能最大
O
B
A
F
F
分析总结:结合下图完成下表
A
B
O
位移:Xm
X=0
Xm
回复力:Fm
F=0
Fm
加速度:am
a=0
am
势能:Epm
Ep=0
Epm
总机械能:
E
E
E
动能:Ek=
0
Ekm
Ek=
0
速度:V=0
Vm
V=0
D
2
A
B
O
X↓
F↓
a↓
V↑
→
→
→
.简谐运动的特点:
1、回复力与位移成正比而方向相反,总是指向平衡位置。
2、简谐运动是一种理想化的运动,振动过程中无阻力,所以振动系统机械能守恒。
3、简谐运动是一种非匀变速运动。
4、具有往复性,对称性、周期性
简谐振动中的对称关系
(1)关于平衡位置的
对称点
①a、F、X大小相同,方向相反;动能势能相同
②V大小相同,方向不一定
(2)先后通过同一位置
①a、F、X,动能势能相同
②V大小相同,方向相反
ABD
3
X大小相同
→
EP相同
→
Ek相同
A
B
O
a
b
振子连续两次通过P位置,下列各量哪些是相同的?
位移(
)
回复力(
)
加速度(
)
动能(
)
势能(
)
速率(
)
速度(
)
动量(
)
√
×
√
√
√
√
√
×
O
B
A
P
x
简谐运动中动能和势能在发生相互转化,但机械能的总量保持不变,即机械能守恒。
试画出物体在做简谐运动时的Ek-t和Ep-t及E-t图象
t
E
0
机械能
势能
动能
A
B
O
简谐运动的能量由劲度系数和振幅决定.
二.简谐运动的能量
从平衡位置开始计时,取向右为正方向
三.简谐运动中各个物理量的变化规律
4
5
AD
C
小结
1、回复力:使振动物体回到平衡位置的力.
2、简谐运动回复力的特点:如果质点所受的回复力与它偏离平衡位置的位移大小成正比,方向相反,(始终指向平衡位置),质点的运动就是简谐运动。
3、简谐运动中动能和势能在发生相互转化,但机械能的总量保持不变,即机械能守恒.
O
分析:
沿振动方向有两个力,弹簧的弹力和重力的分力,二者的合力提供回复力
设平衡时弹簧的伸长量为x0,则有
此时回复力为零,该位置为平衡位置记为O。
若拉长x,则弹力为F∕=k(x0+x)
此时回复力F=F∕-mgsinθ=kx,而F方向与x方向相反。
故
F=
-
kx成立
该振动为简谐运动
x
mgsinθ
F∕
课本第12页第一题
BC
6
A
B
O
BC
7
A
B
O
ABC
8
B处速度为0
放m上时无能量损失
↑
↑
?若在o点轻放m则应选(
)
BD
D
9
a=0
g
↓
↑
g
V
V
V=0
a>g
Vm
向下压缩弹簧
KX
mg
对称性
10
C
整体:kA=(3m/2)am
对于m/2:Ff=(m/2)am
11
AC
A
A-O
O
O-B
B
x
v
F、a
动能
势能
总机械能
向左减小
向右增大
向右减小
动能增大
势能减小
向右增大
向右减小
向左增大
动能减小
势能增大
不变
向左最大
向右最大
0
0
向右最大
0
0
向右最大
向左最大
动能最大
势能为0
动能为0
势能最大
动能为0
势能最大
判断物体是否做简谐运动的方法:
(1)根据物体的振动图像去判断
(2)根据回复力的规律F=-kx去判断
思考:
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
竖直方向振动的弹簧振子所做的振动是简谐运动吗?
【思考题】
判断物体是否做简谐运动的方法:
(2)根据回复力的规律F=-kx去判断
(1)根据物体的振动图像去判断
证明:竖直悬挂的弹簧振子做简谐运动
①找平衡位置
在平衡位置处
②找回复力
指向平衡位置的合力
将小球拉离平衡位置到c点,
此时偏离平衡位置的位移为x,方向向下
方向向上
③找F=kx
x偏离平衡位置的位移
④找方向关系
证明:平衡状态时有:
mg=-kx0
当向下拉动x长度时弹簧所受的合外力为
F=-k(x+x0)+mg
=-kx-kx0+mg
=-kx
(符合简谐运动的公式)
