浙江省湖州市长兴县2020-2021学年下学期九年级 返校考数学试卷(Word版 无答案)
文档属性
| 名称 | 浙江省湖州市长兴县2020-2021学年下学期九年级 返校考数学试卷(Word版 无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 112.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 08:54:43 | ||
图片预览

文档简介
2020-2021学年浙江省湖州市长兴县九年级(下)返校考数学试卷
一、选择题(本题有10小题,每小题3分,共30分)
1.已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
2.一个布袋里装有2个白球和3个黑球,它们除颜色外其余都相同,从袋子里任意摸出1个球,摸到黑球的概率是( )
A. B. C. D.1
3.二次函数y=﹣3(x+1)2﹣2与y轴的交点坐标是( )
A.(﹣1,﹣2) B.(﹣1,2) C.(0,﹣2) D.(0,﹣5)
4.已知抛物线y=﹣x2﹣2x+3,当﹣2?x?2时,对应的函数值y的取值范围为( )
A.﹣5≤y≤2 B.﹣5≤y≤3 C.﹣5≤y≤4 D.﹣5≤y≤5
5.若a+b+c=0,9a﹣3b+c=0,则抛物线y=ax2+bx+c(a≠0)的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线x=﹣2 D.直线x=﹣3
6.点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,BP=4,则线段AP的长为( )
A.4 B.8 C.4 D.4
7.如图,已知在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E,如果CB=8,则线段GE的长为( )
A. B. C. D.
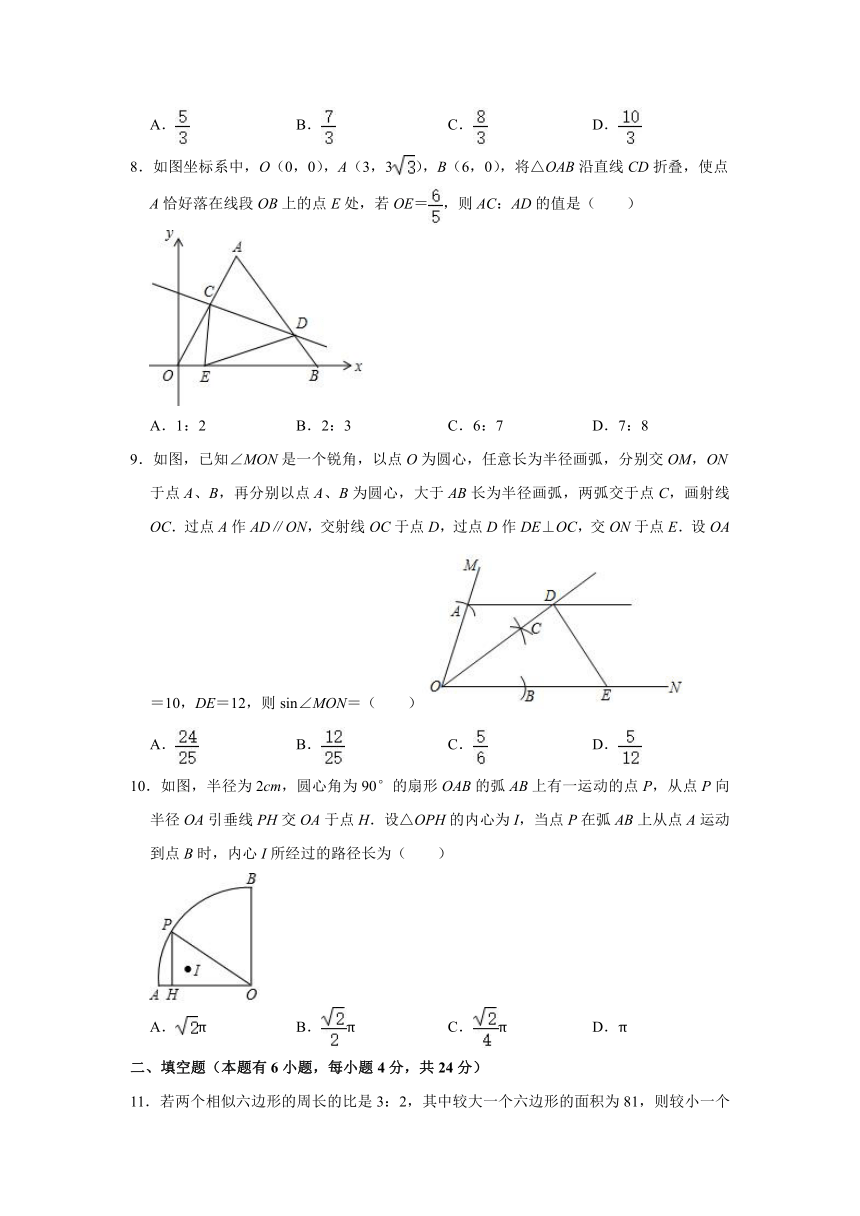
8.如图坐标系中,O(0,0),A(3,3),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=,则AC:AD的值是( )
A.1:2 B.2:3 C.6:7 D.7:8
9.如图,已知∠MON是一个锐角,以点O为圆心,任意长为半径画弧,分别交OM,ON于点A、B,再分别以点A、B为圆心,大于AB长为半径画弧,两弧交于点C,画射线OC.过点A作AD∥ON,交射线OC于点D,过点D作DE⊥OC,交ON于点E.设OA=10,DE=12,则sin∠MON=( )
A. B. C. D.
10.如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A.π B.π C.π D.π
二、填空题(本题有6小题,每小题4分,共24分)
11.若两个相似六边形的周长的比是3:2,其中较大一个六边形的面积为81,则较小一个六边形的面积为 .
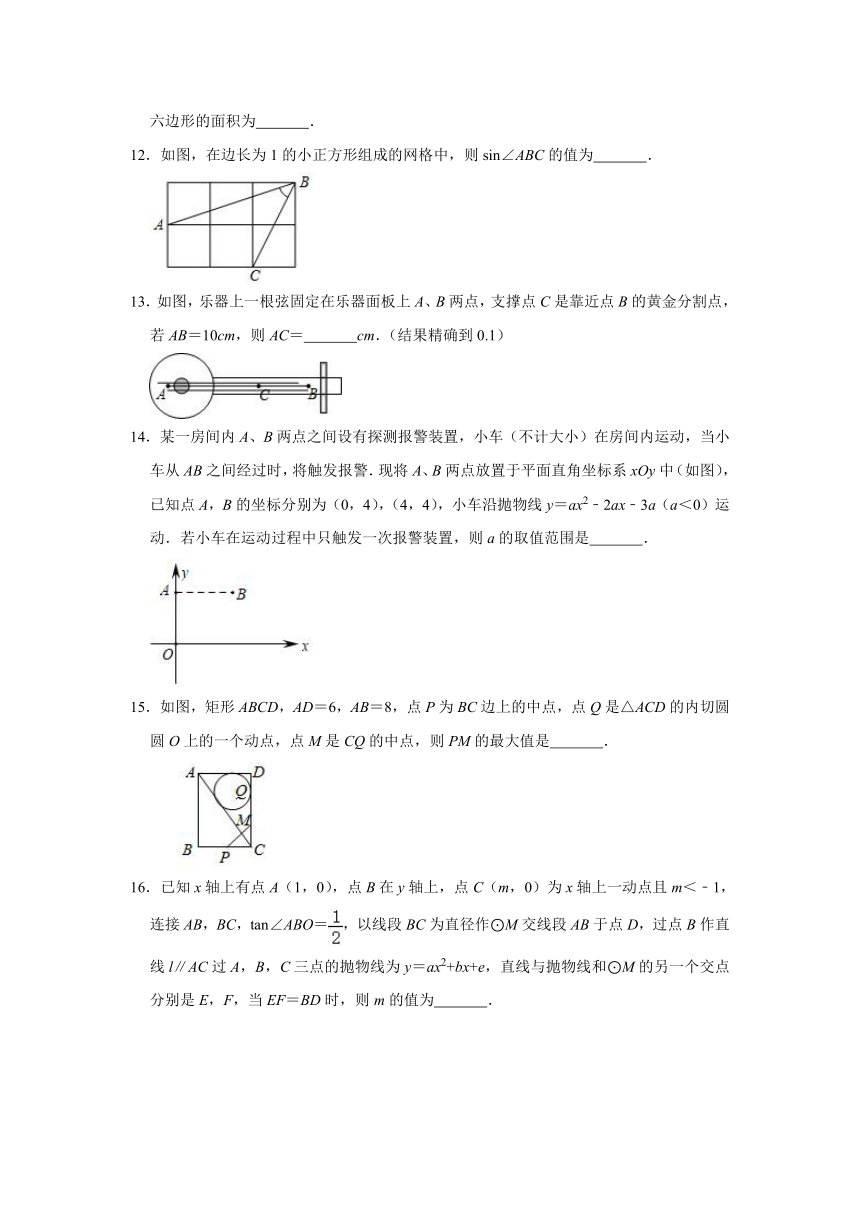
12.如图,在边长为1的小正方形组成的网格中,则sin∠ABC的值为 .
13.如图,乐器上一根弦固定在乐器面板上A、B两点,支撑点C是靠近点B的黄金分割点,若AB=10cm,则AC= cm.(结果精确到0.1)
14.某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间经过时,将触发报警.现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(4,4),小车沿抛物线y=ax2﹣2ax﹣3a(a<0)运动.若小车在运动过程中只触发一次报警装置,则a的取值范围是 .
15.如图,矩形ABCD,AD=6,AB=8,点P为BC边上的中点,点Q是△ACD的内切圆圆O上的一个动点,点M是CQ的中点,则PM的最大值是 .
16.已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO=,以线段BC为直径作⊙M交线段AB于点D,过点B作直线l∥AC过A,B,C三点的抛物线为y=ax2+bx+e,直线与抛物线和⊙M的另一个交点分别是E,F,当EF=BD时,则m的值为 .
三、解答题(本题有8小题,共66分).
17.求值:sin30°+tan45°﹣cos60°.
18.如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同
(1)一只自由飞翔的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少 (用树状图或列表法求解)?
19.如图,抛物线y=﹣x2+bx+c与x轴相交于A(﹣3,0),D(1,0)两点,其中顶点为B.
(1)求该抛物线的解析式;
(2)若该抛物线与y轴的交点为C,求△ABC的面积.
20.如图,在⊙O中,点D为AB的中点,点P为半径OC延长线上一点,连结AC,AP,且AC平分∠PAB.
(1)求证:PA是⊙O的切线;
(2)若AB平分OC,且⊙O的半径为2,求PA的长度.
21.某厂为满足市场需求,改造了10条口罩生产线,每条生产线每天可生产口罩500个,如果每增加一条生产线,每条生产线每天就会少生产20个口罩,设增加x条生产线(x为正整数),每条生产线每天可生产口罩y个.
(1)请直接写出y与x之间的函数关系式和自变量取值范围;
(2)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出当x为多少时,每天生产的口罩数量w最多?最多为多少个?
(3)由于口罩供不应求,所以每天生产的口罩数量不能低于6000个,请直接写出需要增加的生产线x条的取值范围.
22.如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°,当点P位于初始位置P0时,点D与C重合(图2).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.
(1)上午10:00时,太阳光线与地面的夹角为65°(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.1m)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离?(结果精确到0.1m)(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41,≈1.73)
23.(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD?AB;
(2)如图2,在ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE∠A.若BF=5,BE=4,求AD的长.
(3)如图3,在菱形ABCD中,E是△AB上一点.F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=∠BAD,AE=2,AD=5,求DF的长.
24.在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线y=﹣x2﹣x+2与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
一、选择题(本题有10小题,每小题3分,共30分)
1.已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O外 C.点P在⊙O上 D.无法确定
2.一个布袋里装有2个白球和3个黑球,它们除颜色外其余都相同,从袋子里任意摸出1个球,摸到黑球的概率是( )
A. B. C. D.1
3.二次函数y=﹣3(x+1)2﹣2与y轴的交点坐标是( )
A.(﹣1,﹣2) B.(﹣1,2) C.(0,﹣2) D.(0,﹣5)
4.已知抛物线y=﹣x2﹣2x+3,当﹣2?x?2时,对应的函数值y的取值范围为( )
A.﹣5≤y≤2 B.﹣5≤y≤3 C.﹣5≤y≤4 D.﹣5≤y≤5
5.若a+b+c=0,9a﹣3b+c=0,则抛物线y=ax2+bx+c(a≠0)的对称轴是( )
A.直线x=1 B.直线x=﹣1 C.直线x=﹣2 D.直线x=﹣3
6.点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,BP=4,则线段AP的长为( )
A.4 B.8 C.4 D.4
7.如图,已知在Rt△ABC中,∠C=90°,点G是△ABC的重心,GE⊥AC,垂足为E,如果CB=8,则线段GE的长为( )
A. B. C. D.
8.如图坐标系中,O(0,0),A(3,3),B(6,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=,则AC:AD的值是( )
A.1:2 B.2:3 C.6:7 D.7:8
9.如图,已知∠MON是一个锐角,以点O为圆心,任意长为半径画弧,分别交OM,ON于点A、B,再分别以点A、B为圆心,大于AB长为半径画弧,两弧交于点C,画射线OC.过点A作AD∥ON,交射线OC于点D,过点D作DE⊥OC,交ON于点E.设OA=10,DE=12,则sin∠MON=( )
A. B. C. D.
10.如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A.π B.π C.π D.π
二、填空题(本题有6小题,每小题4分,共24分)
11.若两个相似六边形的周长的比是3:2,其中较大一个六边形的面积为81,则较小一个六边形的面积为 .
12.如图,在边长为1的小正方形组成的网格中,则sin∠ABC的值为 .
13.如图,乐器上一根弦固定在乐器面板上A、B两点,支撑点C是靠近点B的黄金分割点,若AB=10cm,则AC= cm.(结果精确到0.1)
14.某一房间内A、B两点之间设有探测报警装置,小车(不计大小)在房间内运动,当小车从AB之间经过时,将触发报警.现将A、B两点放置于平面直角坐标系xOy中(如图),已知点A,B的坐标分别为(0,4),(4,4),小车沿抛物线y=ax2﹣2ax﹣3a(a<0)运动.若小车在运动过程中只触发一次报警装置,则a的取值范围是 .
15.如图,矩形ABCD,AD=6,AB=8,点P为BC边上的中点,点Q是△ACD的内切圆圆O上的一个动点,点M是CQ的中点,则PM的最大值是 .
16.已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO=,以线段BC为直径作⊙M交线段AB于点D,过点B作直线l∥AC过A,B,C三点的抛物线为y=ax2+bx+e,直线与抛物线和⊙M的另一个交点分别是E,F,当EF=BD时,则m的值为 .
三、解答题(本题有8小题,共66分).
17.求值:sin30°+tan45°﹣cos60°.
18.如图所示的方格地面上,标有编号1、2、3的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同
(1)一只自由飞翔的小鸟,将随意地落在图中所示的方格地面上,求小鸟落在草坪上的概率;
(2)现准备从图中所示的3个小方格空地中任意选取2个种植草坪,则编号为1、2的2个小方格空地种植草坪的概率是多少 (用树状图或列表法求解)?
19.如图,抛物线y=﹣x2+bx+c与x轴相交于A(﹣3,0),D(1,0)两点,其中顶点为B.
(1)求该抛物线的解析式;
(2)若该抛物线与y轴的交点为C,求△ABC的面积.
20.如图,在⊙O中,点D为AB的中点,点P为半径OC延长线上一点,连结AC,AP,且AC平分∠PAB.
(1)求证:PA是⊙O的切线;
(2)若AB平分OC,且⊙O的半径为2,求PA的长度.
21.某厂为满足市场需求,改造了10条口罩生产线,每条生产线每天可生产口罩500个,如果每增加一条生产线,每条生产线每天就会少生产20个口罩,设增加x条生产线(x为正整数),每条生产线每天可生产口罩y个.
(1)请直接写出y与x之间的函数关系式和自变量取值范围;
(2)设该厂每天可以生产的口罩w个,请求出w与x的函数关系式,并求出当x为多少时,每天生产的口罩数量w最多?最多为多少个?
(3)由于口罩供不应求,所以每天生产的口罩数量不能低于6000个,请直接写出需要增加的生产线x条的取值范围.
22.如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°,当点P位于初始位置P0时,点D与C重合(图2).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.
(1)上午10:00时,太阳光线与地面的夹角为65°(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.1m)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离?(结果精确到0.1m)(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41,≈1.73)
23.(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=AD?AB;
(2)如图2,在ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE∠A.若BF=5,BE=4,求AD的长.
(3)如图3,在菱形ABCD中,E是△AB上一点.F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=∠BAD,AE=2,AD=5,求DF的长.
24.在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.
已知抛物线y=﹣x2﹣x+2与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
同课章节目录
