七年级数学相交线、平行线复习
文档属性
| 名称 | 七年级数学相交线、平行线复习 |  | |
| 格式 | rar | ||
| 文件大小 | 228.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-08 17:15:43 | ||
图片预览


文档简介
(共13张PPT)
第二章、相交线、平行线
————复习课
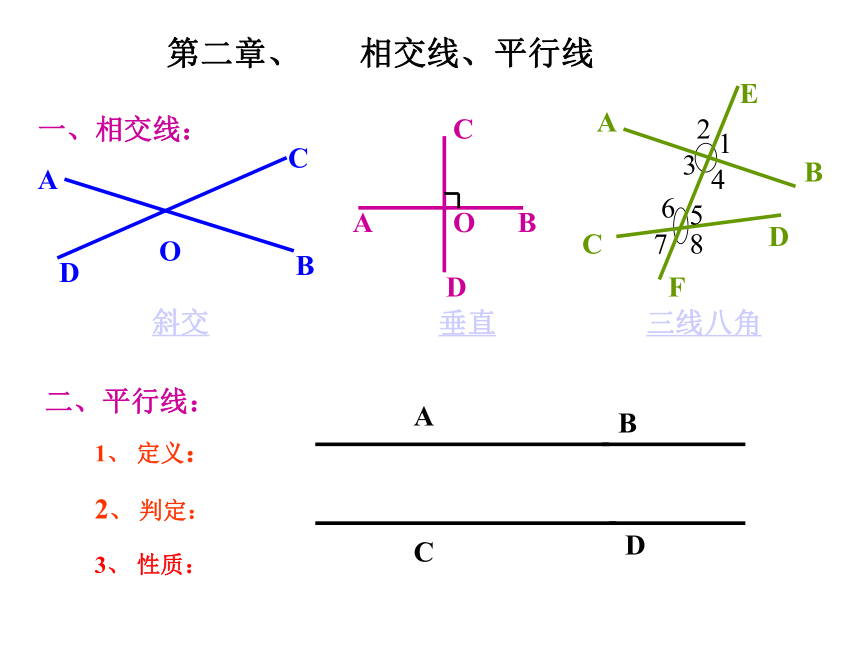
第二章、 相交线、平行线
一、相交线:
A
B
C
D
O
A
B
C
D
O
7
2
4
A
B
C
D
E
F
1
3
5
6
8
二、平行线:
A
B
C
D
1、 定义:
2、 判定:
垂直
3、 性质:
斜交
三线八角
A
C
B
D
1
2
3
4
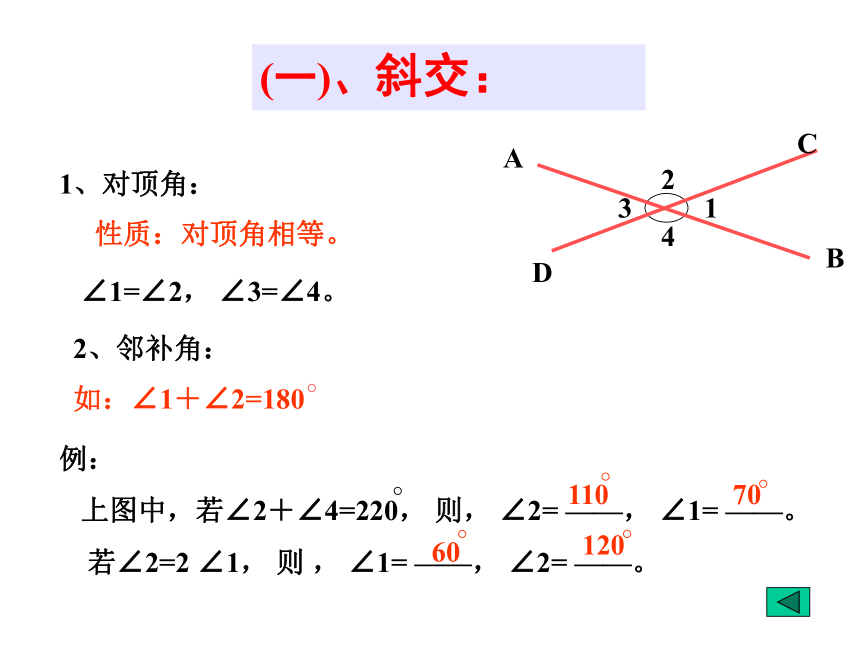
1、对顶角:
性质:对顶角相等。
2、邻补角:
如:∠1+∠2=180
∠1=∠2, ∠3=∠4。
例:
上图中,若∠2+∠4=220, 则, ∠2= ——, ∠1= ——。
若∠2=2 ∠1, 则 , ∠1= ——, ∠2= ——。
110
70
60
120
(一)、斜交:
A
B
C
D
O
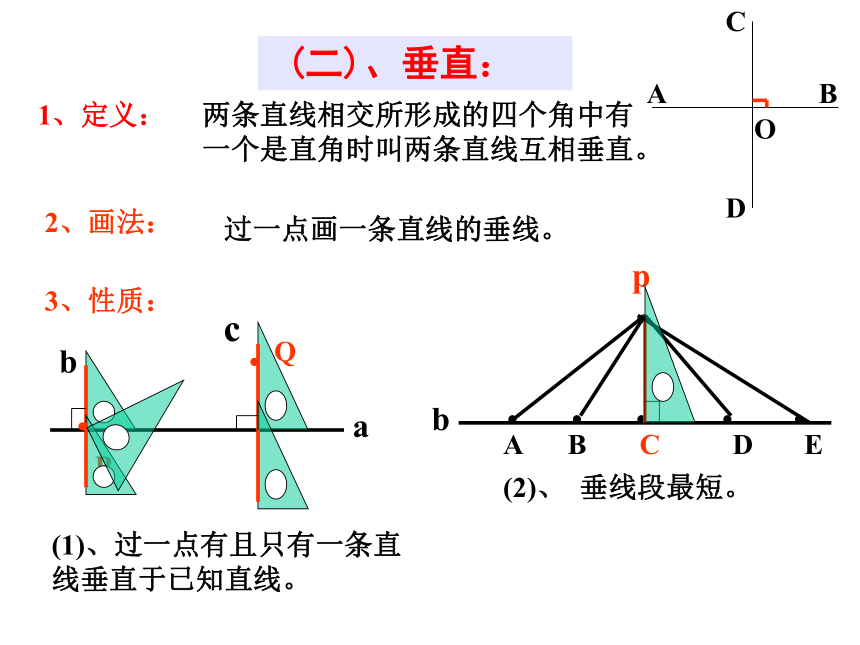
(二)、垂直:
2、画法:
3、性质:
两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直。
过一点画一条直线的垂线。
P
a
Q
(1)、过一点有且只有一条直线垂直于已知直线。
p
A
B
C
D
E
(2)、 垂线段最短。
b
b
c
1、定义:
点到直线的距离: 从直线外一点到这条直线的 垂线段的长度,叫做这点到这条直线的距离.
判断:
1、画出点A到直线BC的距离。( )
2、画出点A到直线BC的垂线段。( )
3、量出点A到直线BC的距离。 ( )
4、垂线最短。 ( )
B
C
A
D
A
B
C
D
E
F
1
2
3
4
5
6
7
8
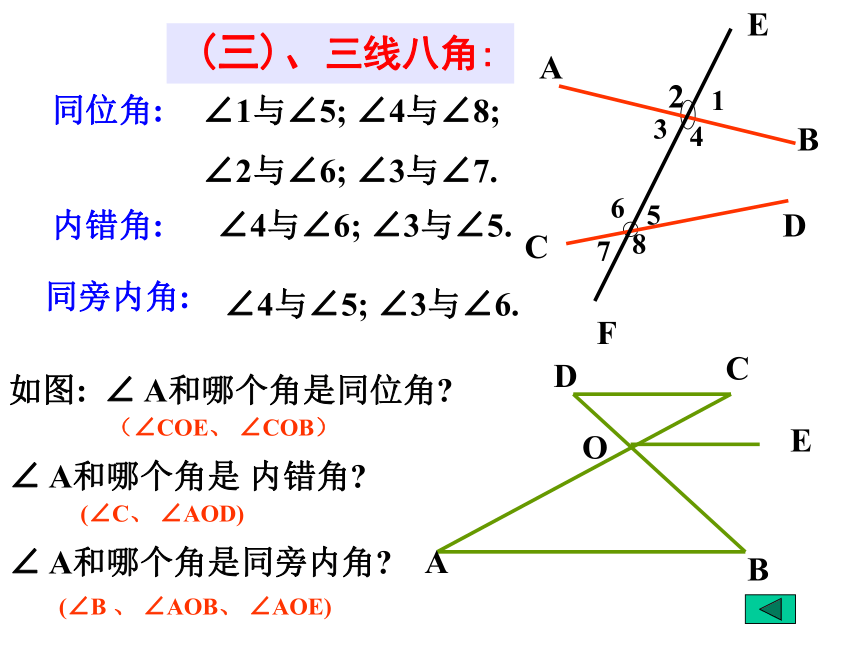
同位角:
内错角:
同旁内角:
∠1与∠5; ∠4与∠8;
∠2与∠6; ∠3与∠7.
∠4与∠6; ∠3与∠5.
∠4与∠5; ∠3与∠6.
A
B
C
D
E
O
如图: ∠ A和哪个角是同位角
∠ A和哪个角是 内错角
∠ A和哪个角是同旁内角
(∠COE、 ∠COB)
(∠C、 ∠AOD)
(∠B 、 ∠AOB、 ∠AOE)
(三)、三线八角:
如图: 已知: b∥c, a是截线,并且a⊥b.
求证: a ⊥c .
a
b
c
1
2
(已知)
(垂直定义)
(已知)
(两直线平行,同位角相等)
(垂直定义)
∠1=90
∴
b∥c
又∵
a ⊥b
∵
a ⊥c.
∴
∠2= ∠1=90
∴
证明:
A
B
C
D
a
b
(一)、定义:
在同一平面内,不相交的两条直线叫做平行线。
(二)、判定:
1、定义。
2、同位角相等,两直线平行。
1
2
3
4
5
6
7
8
3、 内错角相等,两直线平行。
4、 同旁内角互补,两直线平行。
c
6、在同一平面内,垂直于同一直线的
二直线互相平行。
5、平行于同一直线的二直线互 相平行。
a
b
c
二、平行线
E
F
A
B
C
D
E
F
1
2
3
4
5
6
如图: 填空,并注明理由。
(1)、∵ ∠1= ∠2 (已知)
——∥—— ( )
∵ ∠3= ∠4 (已知)
——∥—— ( )
∵ ∠5= ∠6 (已知)
——∥—— ( )
∵ ∠5+ ∠AFE=180 (已知)
——∥—— ( )
∵ AB ∥FC, ED ∥FC (已知)
——∥—— ( )
∴
∴
∴
∴
∴
AB
ED
内错角相等。两直线平行,
AF
BE
同位角相等,两直线平行。
BC
EF
内错角相等,两直线平行。
AF
BE
同旁内角互补,两直线平行。
AB
ED
平行于同直线的两条直线互相平行。
平行线的判定应用练习:
A
B
C
D
E
F
1
2
3
4
5
6
7
8
(三)、平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
c
a
b
1
3
4
2
应用举例:
如图:a∥b, ∠1=50 ,
则,∠2=_____.
若, ∠3=100 ,则, ∠2=____.
若, ∠3=120 , 则, ∠4=——。
50
80
60
性质:
同位角相等 ,两直线平行。
内错角相等 ,两直线平行。
同旁内角互补 , 两直线平行。
判定:
综合应用:
A
B
C
D
E
F
1
2
3
1、填空:
(1)、∵ ∠A=____, (已知)
AC∥ED ,(_____________________)
(2)、 ∵AB ∥______, (已知)
∠2= ∠4,(______________________)
4
5
(3)、 ___ ∥___, (已知)
∠B= ∠3. (___________ ___________)
试一试,你准行!
模仿上题自己编题。(考查平行线的性质或判定)
∠4
同位角相等,两直线平行。
DF
两直线平行, 内错角相等。
AB
DF
两直线平行, 同位角相等.
判定
性质
性质
∴
∴
∴
∵
1.四边行ABCD中, AB∥CD, AD∥BC.
试说明∠A=∠C, ∠B=∠D.
证明:∵AB∥CD ﹙已知﹚
∴∠B+∠C=1800 ﹙两直线平行,同旁内角互补﹚
∴∠A+∠B=1800 ﹙两直线平行,
同旁内角互补 ﹚
∴∠A=∠C ﹙同角的补角相等﹚
同理:∠B=∠D
∵AD∥BC ﹙已知﹚
2,如图所示,已知D.E.F和A.B.C
A
E
F
2
3
1
D
C
B
分别在同一直线上,∠1=∠2,∠C=∠D
求证:DF∥AC
证明:∵∠1= ∠2( )
∠1=∠3( ) ∴∠2=∠3( )
∴DB∥EC( )
∴∠C=∠DBA( )
∵∠C=∠D( ) ∴∠D=∠DBA( )
∴DF∥EC( )
第二章、相交线、平行线
————复习课
第二章、 相交线、平行线
一、相交线:
A
B
C
D
O
A
B
C
D
O
7
2
4
A
B
C
D
E
F
1
3
5
6
8
二、平行线:
A
B
C
D
1、 定义:
2、 判定:
垂直
3、 性质:
斜交
三线八角
A
C
B
D
1
2
3
4
1、对顶角:
性质:对顶角相等。
2、邻补角:
如:∠1+∠2=180
∠1=∠2, ∠3=∠4。
例:
上图中,若∠2+∠4=220, 则, ∠2= ——, ∠1= ——。
若∠2=2 ∠1, 则 , ∠1= ——, ∠2= ——。
110
70
60
120
(一)、斜交:
A
B
C
D
O
(二)、垂直:
2、画法:
3、性质:
两条直线相交所形成的四个角中有一个是直角时叫两条直线互相垂直。
过一点画一条直线的垂线。
P
a
Q
(1)、过一点有且只有一条直线垂直于已知直线。
p
A
B
C
D
E
(2)、 垂线段最短。
b
b
c
1、定义:
点到直线的距离: 从直线外一点到这条直线的 垂线段的长度,叫做这点到这条直线的距离.
判断:
1、画出点A到直线BC的距离。( )
2、画出点A到直线BC的垂线段。( )
3、量出点A到直线BC的距离。 ( )
4、垂线最短。 ( )
B
C
A
D
A
B
C
D
E
F
1
2
3
4
5
6
7
8
同位角:
内错角:
同旁内角:
∠1与∠5; ∠4与∠8;
∠2与∠6; ∠3与∠7.
∠4与∠6; ∠3与∠5.
∠4与∠5; ∠3与∠6.
A
B
C
D
E
O
如图: ∠ A和哪个角是同位角
∠ A和哪个角是 内错角
∠ A和哪个角是同旁内角
(∠COE、 ∠COB)
(∠C、 ∠AOD)
(∠B 、 ∠AOB、 ∠AOE)
(三)、三线八角:
如图: 已知: b∥c, a是截线,并且a⊥b.
求证: a ⊥c .
a
b
c
1
2
(已知)
(垂直定义)
(已知)
(两直线平行,同位角相等)
(垂直定义)
∠1=90
∴
b∥c
又∵
a ⊥b
∵
a ⊥c.
∴
∠2= ∠1=90
∴
证明:
A
B
C
D
a
b
(一)、定义:
在同一平面内,不相交的两条直线叫做平行线。
(二)、判定:
1、定义。
2、同位角相等,两直线平行。
1
2
3
4
5
6
7
8
3、 内错角相等,两直线平行。
4、 同旁内角互补,两直线平行。
c
6、在同一平面内,垂直于同一直线的
二直线互相平行。
5、平行于同一直线的二直线互 相平行。
a
b
c
二、平行线
E
F
A
B
C
D
E
F
1
2
3
4
5
6
如图: 填空,并注明理由。
(1)、∵ ∠1= ∠2 (已知)
——∥—— ( )
∵ ∠3= ∠4 (已知)
——∥—— ( )
∵ ∠5= ∠6 (已知)
——∥—— ( )
∵ ∠5+ ∠AFE=180 (已知)
——∥—— ( )
∵ AB ∥FC, ED ∥FC (已知)
——∥—— ( )
∴
∴
∴
∴
∴
AB
ED
内错角相等。两直线平行,
AF
BE
同位角相等,两直线平行。
BC
EF
内错角相等,两直线平行。
AF
BE
同旁内角互补,两直线平行。
AB
ED
平行于同直线的两条直线互相平行。
平行线的判定应用练习:
A
B
C
D
E
F
1
2
3
4
5
6
7
8
(三)、平行线的性质:
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
c
a
b
1
3
4
2
应用举例:
如图:a∥b, ∠1=50 ,
则,∠2=_____.
若, ∠3=100 ,则, ∠2=____.
若, ∠3=120 , 则, ∠4=——。
50
80
60
性质:
同位角相等 ,两直线平行。
内错角相等 ,两直线平行。
同旁内角互补 , 两直线平行。
判定:
综合应用:
A
B
C
D
E
F
1
2
3
1、填空:
(1)、∵ ∠A=____, (已知)
AC∥ED ,(_____________________)
(2)、 ∵AB ∥______, (已知)
∠2= ∠4,(______________________)
4
5
(3)、 ___ ∥___, (已知)
∠B= ∠3. (___________ ___________)
试一试,你准行!
模仿上题自己编题。(考查平行线的性质或判定)
∠4
同位角相等,两直线平行。
DF
两直线平行, 内错角相等。
AB
DF
两直线平行, 同位角相等.
判定
性质
性质
∴
∴
∴
∵
1.四边行ABCD中, AB∥CD, AD∥BC.
试说明∠A=∠C, ∠B=∠D.
证明:∵AB∥CD ﹙已知﹚
∴∠B+∠C=1800 ﹙两直线平行,同旁内角互补﹚
∴∠A+∠B=1800 ﹙两直线平行,
同旁内角互补 ﹚
∴∠A=∠C ﹙同角的补角相等﹚
同理:∠B=∠D
∵AD∥BC ﹙已知﹚
2,如图所示,已知D.E.F和A.B.C
A
E
F
2
3
1
D
C
B
分别在同一直线上,∠1=∠2,∠C=∠D
求证:DF∥AC
证明:∵∠1= ∠2( )
∠1=∠3( ) ∴∠2=∠3( )
∴DB∥EC( )
∴∠C=∠DBA( )
∵∠C=∠D( ) ∴∠D=∠DBA( )
∴DF∥EC( )
