高中数学人教A版必修4课件-1.1.1任意角(18张PPT)
文档属性
| 名称 | 高中数学人教A版必修4课件-1.1.1任意角(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 20:30:41 | ||
图片预览




文档简介
1.1.1任意角
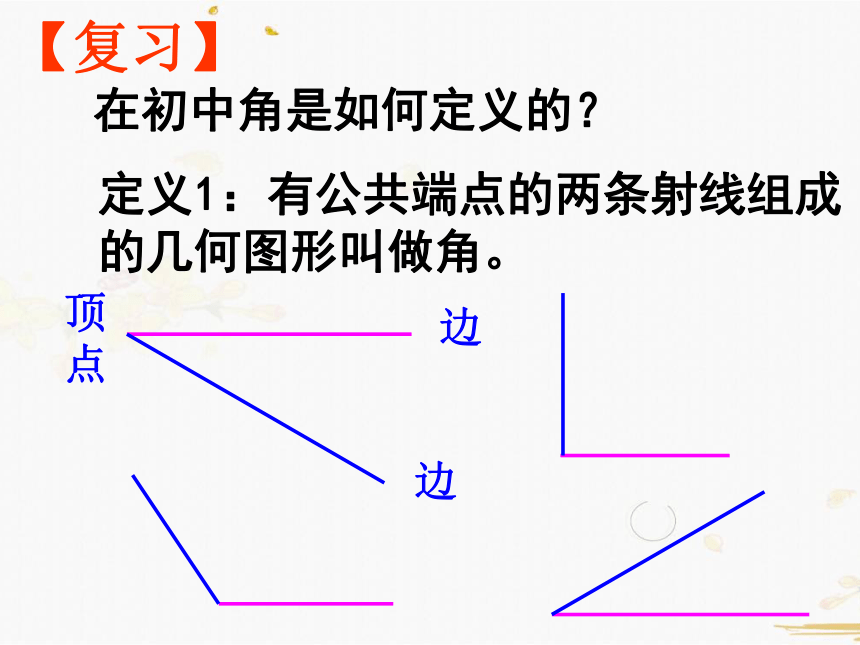
在初中角是如何定义的?
定义1:有公共端点的两条射线组成的几何图形叫做角。
顶点
边
边
【复习】
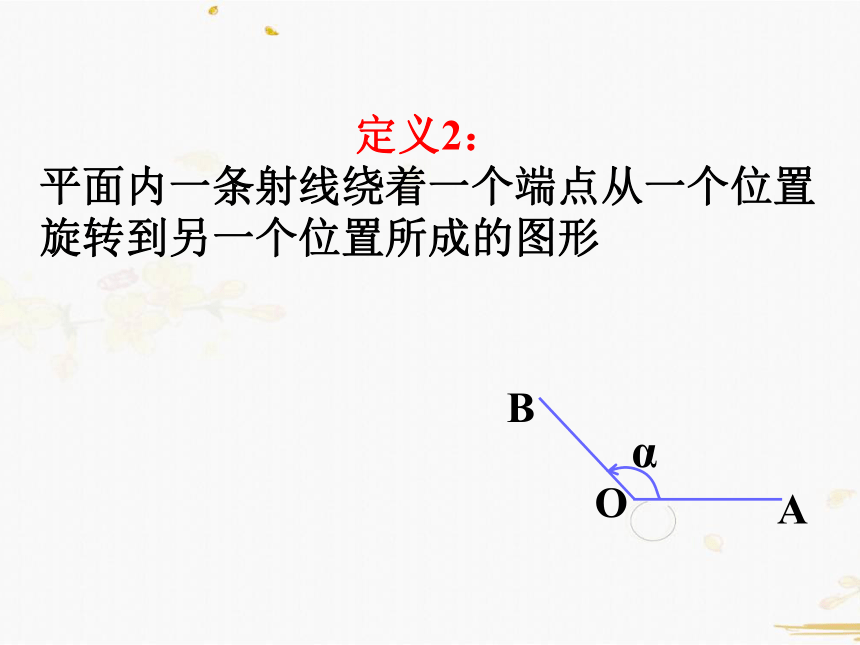
定义2:
平面内一条射线绕着一个端点从一个位置旋转到另一个位置所成的图形
O
A
B
α
体操上有直体后空翻转体720度的高难度动作,直体前空翻转体360度接直体前空翻转体540度,俄式挺身转体1080度,直体后空翻转体900度以及团身后空翻两周转体360度
现实中其它角
现实中其它角
旋转方向也有顺时针与逆时针
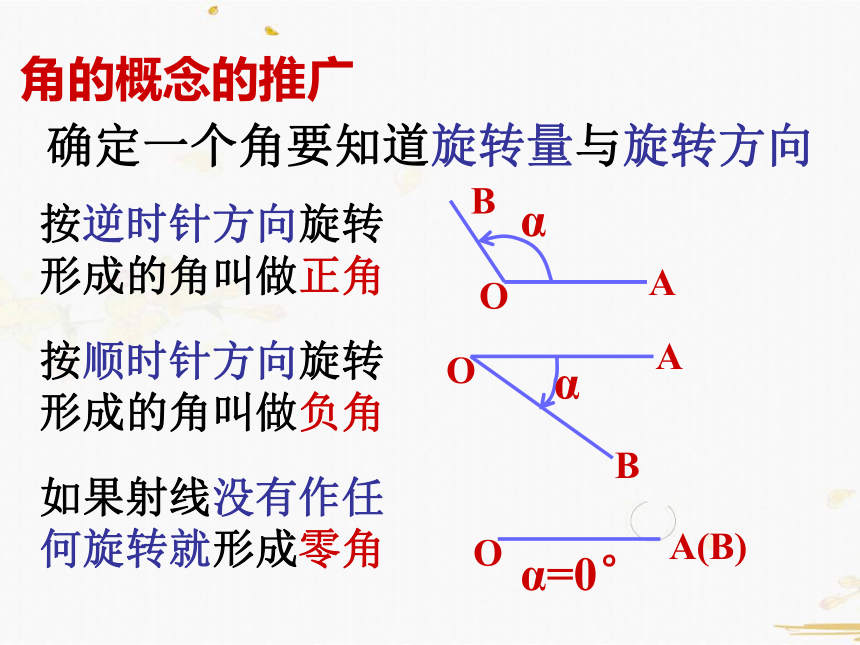
按逆时针方向旋转形成的角叫做正角
按顺时针方向旋转形成的角叫做负角
如果射线没有作任何旋转就形成零角
角的概念的推广
确定一个角要知道旋转量与旋转方向
O
A(B)
O
B
A
α
O
A
B
α
α=0°
为了简单起见,在不引起混淆的前提下,"角α"或"∠α"可简记为α
这样,我们就把角的概念推广到了任意角:包括正角、负角、零角
在今后的学习中,我们常在直角坐标系内讨论角,为此我们必须了解象限角这个概念.
-120°
30°
x
y
角的顶点与原点重合,角的始边与x轴的非负半轴重合.那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角.
第一象限角
第三象限角
注意:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角.
将角按上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系中任意一条射线 OB,以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
探究
x
y
o
B
-32°的终边是OB,
而328°,-392°·······角的终边都是OB
328°=-32°+360°
-392°=-32°-360°
与-32°终边相同的角与-32°相差k个(k∈Z)周角的和.
设S={β|β=-32°+k·360°,k∈Z}
328°∈S, -392°∈S, -32°∈S
与32°终边相同的角,连同-32°角都是S的元素;
S里的元素与-32°角的终边相同.
探究分析
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+k·360°,k∈Z}
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
例1 在0°~360°范围内,找出与
-950°12′角终边相同的角,并判定它是第几象限角.
解: -950°12′=129°48′-3×360°
所以在0°~360°范围内,与-950°12′角终边相同的角是129°48′,它是第二象限角.
判断一个角是第几象限角,一般方法是: 所给角 改写成 : 0 + k ·3600 ( K∈Z,00≤ 0<3600)的形式, 0在第几象限 就是第几象限角
例2 写出终边在y轴上的角的集合.
y
x
o
270°
90°
解:与90°终边相同的角构成集合
S1={β|β=90°+k·360°,k∈Z}
与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z}
终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+k·360°,k∈Z}
∪{β|β=270°+k·360°,k∈Z}
={β|β=90°+2k·180°,k∈Z}
∪{β|β=90°+(2k+1)·180°,k∈Z}
={β|β=90°+n·180°,n∈Z}
例3 写出终边在直线y=x上的角的集合S,并把S中适合不等式
-360°≤β<720°的元素β写出来.
x
O
y
225°
45°
解:终边在直线y=x上的角的集合
S={β|β=45°+k·360°,k∈Z}
∪{β|β=225°+k·360°,k∈Z}
={β|β=45°+k·180°,k∈Z}
课堂练习
P5练习1、2、3、4、5
小结:
1.任意角
的概念
正角:射线按逆时针方向旋转形成的角
负角:射线按顺时针方向旋转形成的角
零角:射线不作旋转形成的角
1)把角的顶点放在原点
2)始边重合于X轴的非负半轴
2.象限角
终边落在第几象限就是第几象限角
3 . 终边与 角a相同的角
+K·3600,K∈Z
作业布置
课本第9页A组第1、2、3题。
在初中角是如何定义的?
定义1:有公共端点的两条射线组成的几何图形叫做角。
顶点
边
边
【复习】
定义2:
平面内一条射线绕着一个端点从一个位置旋转到另一个位置所成的图形
O
A
B
α
体操上有直体后空翻转体720度的高难度动作,直体前空翻转体360度接直体前空翻转体540度,俄式挺身转体1080度,直体后空翻转体900度以及团身后空翻两周转体360度
现实中其它角
现实中其它角
旋转方向也有顺时针与逆时针
按逆时针方向旋转形成的角叫做正角
按顺时针方向旋转形成的角叫做负角
如果射线没有作任何旋转就形成零角
角的概念的推广
确定一个角要知道旋转量与旋转方向
O
A(B)
O
B
A
α
O
A
B
α
α=0°
为了简单起见,在不引起混淆的前提下,"角α"或"∠α"可简记为α
这样,我们就把角的概念推广到了任意角:包括正角、负角、零角
在今后的学习中,我们常在直角坐标系内讨论角,为此我们必须了解象限角这个概念.
-120°
30°
x
y
角的顶点与原点重合,角的始边与x轴的非负半轴重合.那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角.
第一象限角
第三象限角
注意:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限,称为非象限角.
将角按上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系中任意一条射线 OB,以它为终边的角是否唯一?如果不唯一,那么终边相同的角有什么关系?
探究
x
y
o
B
-32°的终边是OB,
而328°,-392°·······角的终边都是OB
328°=-32°+360°
-392°=-32°-360°
与-32°终边相同的角与-32°相差k个(k∈Z)周角的和.
设S={β|β=-32°+k·360°,k∈Z}
328°∈S, -392°∈S, -32°∈S
与32°终边相同的角,连同-32°角都是S的元素;
S里的元素与-32°角的终边相同.
探究分析
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+k·360°,k∈Z}
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
例1 在0°~360°范围内,找出与
-950°12′角终边相同的角,并判定它是第几象限角.
解: -950°12′=129°48′-3×360°
所以在0°~360°范围内,与-950°12′角终边相同的角是129°48′,它是第二象限角.
判断一个角是第几象限角,一般方法是: 所给角 改写成 : 0 + k ·3600 ( K∈Z,00≤ 0<3600)的形式, 0在第几象限 就是第几象限角
例2 写出终边在y轴上的角的集合.
y
x
o
270°
90°
解:与90°终边相同的角构成集合
S1={β|β=90°+k·360°,k∈Z}
与270°角终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z}
终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+k·360°,k∈Z}
∪{β|β=270°+k·360°,k∈Z}
={β|β=90°+2k·180°,k∈Z}
∪{β|β=90°+(2k+1)·180°,k∈Z}
={β|β=90°+n·180°,n∈Z}
例3 写出终边在直线y=x上的角的集合S,并把S中适合不等式
-360°≤β<720°的元素β写出来.
x
O
y
225°
45°
解:终边在直线y=x上的角的集合
S={β|β=45°+k·360°,k∈Z}
∪{β|β=225°+k·360°,k∈Z}
={β|β=45°+k·180°,k∈Z}
课堂练习
P5练习1、2、3、4、5
小结:
1.任意角
的概念
正角:射线按逆时针方向旋转形成的角
负角:射线按顺时针方向旋转形成的角
零角:射线不作旋转形成的角
1)把角的顶点放在原点
2)始边重合于X轴的非负半轴
2.象限角
终边落在第几象限就是第几象限角
3 . 终边与 角a相同的角
+K·3600,K∈Z
作业布置
课本第9页A组第1、2、3题。
