高中数学人教A版必修4课件-1.2.1任意角的三角函数 2课时(33张PPT)
文档属性
| 名称 | 高中数学人教A版必修4课件-1.2.1任意角的三角函数 2课时(33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 21:45:43 | ||
图片预览










文档简介
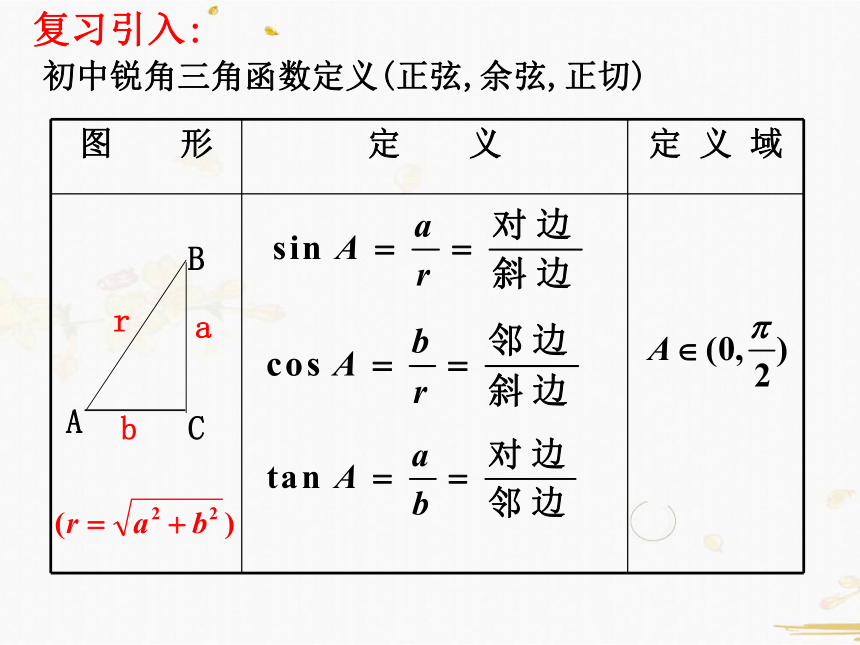
复习引入:
图 形
定 义
定 义 域
初中锐角三角函数定义(正弦,余弦,正切)
b
A
B
r
a
C
角的范围已经推广,那么对任意角是否也能像锐角一样定义其三角函数吗?
思考
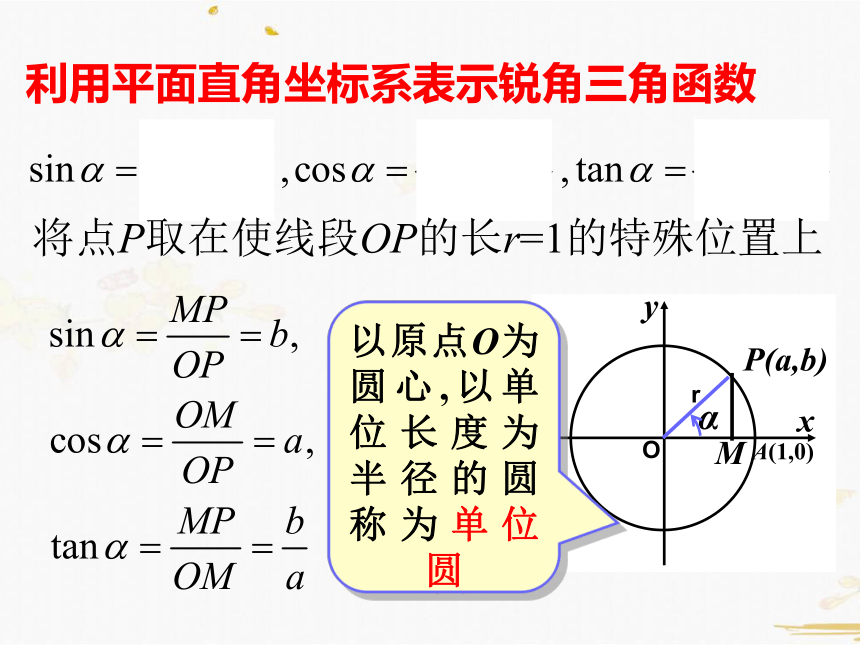
利用平面直角坐标系表示锐角三角函数
M
y
x
O
α
P(a,b)
设锐角α的顶点与原点O重合,始边与x轴的正半轴重合,那么它的终边在第一象限.
α的终边上任意一点P的坐标为(a,b),它与原点的距离是_______________
过P作x轴的垂线,垂足为M,则
线段OM的长度为___
线段MP的长度为___
利用平面直角坐标系表示锐角三角函数
将点P取在使线段OP的长r=1的特殊位置上
P(a,b)
M
A(1,0)
x
y
α
r
以原点O为圆心,以单位长度为半径的圆称为单位圆
O
P(x,y)
A(1,0)
x
y
α
利用单位圆定义任意角的三角函数
设α是一个任意角,它的终边与单位圆交于点P(x,y)
(1)y叫做α的正弦,记作sinα,
即 sinα=y
(2)x叫做α的余弦,记作cosα,
即 cosα=x
(3) 叫做α正切,记作tanα,
即
O
最常用
三角函数的一般定义
注意:
正弦、余弦、正切统称为三角函数,都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数。
弧度制下,角的集合与实数集R之间建立了一一对应关系
三角函数可以看成自变量为实数的函数
y
x
B
A
O
解: 在直角坐标系中,作出
单位圆
方法:用三角函数的单位圆的定义做
例2 已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值。
y
x
O
P0(-3,-4)
解:
方法:用三角函数的一般定义做
α
练 习
课本第15页第1、2题
作业布置
P20—21页第2、3、4题
1. 任意角的三角函数单位圆定义
复习回顾
设α是一个任意角,它的终边与
单位圆交于点P(x,y),那么:
正弦 sinα=
余弦 cosα=
正切 tanα=
(x≠0)
?
x
o
y
P(x,y)
1
y
x
2、三角函数的一般定义
三角函数的定义域
三角函数
定义域
sinα
cosα
tanα
R
R
y
x
o
+
-
+
+
+
+
+
-
-
-
-
-
y
x
o
y
x
o
三角函数在各象限的符号
填表:坐标轴上的三角函数
角α
0°
90°
180°
270°
360°
角α的弧度数
sinα
cosα
tanα
例3 求证:当且仅当下列不等式组成立时,角θ为第三角限角.反之也对.
①
②
证明:如果①②式都成立,那么θ为第三象限角.
若sinθ<0,那么θ角的终边可能位于第三或第四象限,也可能位于y轴的非正半轴上
又若tanθ>0,那么θ角的终边可能位于第一或第三象限.
因为①②式都成立,所以θ角的终边只能位于第三象限.于是θ为第三象限角
反过来自己证
可以把求任意角的三角函数值转化为求0到2π(或0°至360°)角的三角函数值.
终边相同的角的同一三角函数值相等
公式一
角α终边每绕原点旋转一周,函数值将重复出现
例4 确定下列三角函数值的符号,然后用计算器验证:
解:(1)因为250°是第___象限角,所以cos250° 0
(2)因为 是第____象限角,所以
(3)因为tan(-672°)=tan(48°-2×360°)=tan48°
而48°是第一象限角,所以 tan(-672°) 0
(4)因为tan3π=tan(π+2π)=tanπ=0
三
<
四
<
>
例5 求下列三角函数值
练 习
课本第15页第5—7题
作业布置
P20—21页第1、6、7题
三角函数线
设任意角?顶点在原点O,始边与x轴非负半轴重合,终边与单位圆相交与点P(x,y),过P作x轴的垂线,垂足为M;过点A(1,0)作单位圆的切线,它与角?的终边或其反向延长线交与点T.
(Ⅰ)
x
y
o
A(1,0)
α的终边
T
P
M
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅱ)
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅳ)
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅱ)
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅲ)
(Ⅰ)
x
y
o
A(1,0)
α的终边
T
P
M
规定:与坐标轴方向一致时为正,与坐标方向相反时为负.
有向线段:规定了方向的线段.
A
B
x
y
o
C
D
有向线段AB:方向A→B;记作
有向线段BA:方向B→A ;记作
有向线段CD:方向C→D,等.
值为正
值为负
当?为第一或二象限角时, y为正,有sin?=y=|MP|,
而当?为第三或四象限角时,y为负,有sin?=y=-|MP|.
探究:能不能去掉绝对值符号,使得线段OM,MP的值与坐标的正负是一致呢?怎样规定?
有向线段的书写: 有向线段的起点字母在前,终点字母在后面.
(Ⅰ)
x
y
o
A(1,0)
α的终边
T
P
M
这样当角 的终边不在坐标轴上时,我们把 , 都看成有向线段。由正弦、余弦、正切函数的定义有:
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅲ)
三角函数线定义
有向线段MP、OM、AT分别称为正弦线、余弦线、正切线.
统称为三角函数线.(它是三角函数值的一种几何表示法)
当角 的终边在 轴上时,正弦线、正切线分别
变成一个点;此时角 的正弦值和正切值都为0.
当角 的终边在 轴上时,余弦线变成一个点,正切线不存在,此时角 的正切值不存在.
说明:
① 三条有向线段的位置:正弦线为?的终边与单位圆的交点到x轴的垂直线段;余弦线在x轴上;正切线在过单位圆与x轴正方向的交点的切线上,三条有向线段中两条在单位圆内,一条在单位圆外。
② 三条有向线段的正负:三条有向线段凡与x轴或y轴同向的为正值,与x轴或y轴反向的为负值。
课堂小结
1.三角函数线是三角函数的一种几何表示,即用有向线段表示三角函数值,是今后进一步研究三角函数图象的有效工具.
2.三角函数线:用有向线段的数量来表示。
O
x
y
P
M
A
T
3.终边相同的角的同一三角函数值相等.
图 形
定 义
定 义 域
初中锐角三角函数定义(正弦,余弦,正切)
b
A
B
r
a
C
角的范围已经推广,那么对任意角是否也能像锐角一样定义其三角函数吗?
思考
利用平面直角坐标系表示锐角三角函数
M
y
x
O
α
P(a,b)
设锐角α的顶点与原点O重合,始边与x轴的正半轴重合,那么它的终边在第一象限.
α的终边上任意一点P的坐标为(a,b),它与原点的距离是_______________
过P作x轴的垂线,垂足为M,则
线段OM的长度为___
线段MP的长度为___
利用平面直角坐标系表示锐角三角函数
将点P取在使线段OP的长r=1的特殊位置上
P(a,b)
M
A(1,0)
x
y
α
r
以原点O为圆心,以单位长度为半径的圆称为单位圆
O
P(x,y)
A(1,0)
x
y
α
利用单位圆定义任意角的三角函数
设α是一个任意角,它的终边与单位圆交于点P(x,y)
(1)y叫做α的正弦,记作sinα,
即 sinα=y
(2)x叫做α的余弦,记作cosα,
即 cosα=x
(3) 叫做α正切,记作tanα,
即
O
最常用
三角函数的一般定义
注意:
正弦、余弦、正切统称为三角函数,都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数。
弧度制下,角的集合与实数集R之间建立了一一对应关系
三角函数可以看成自变量为实数的函数
y
x
B
A
O
解: 在直角坐标系中,作出
单位圆
方法:用三角函数的单位圆的定义做
例2 已知角α的终边经过点P0(-3,-4),求角α的正弦、余弦和正切值。
y
x
O
P0(-3,-4)
解:
方法:用三角函数的一般定义做
α
练 习
课本第15页第1、2题
作业布置
P20—21页第2、3、4题
1. 任意角的三角函数单位圆定义
复习回顾
设α是一个任意角,它的终边与
单位圆交于点P(x,y),那么:
正弦 sinα=
余弦 cosα=
正切 tanα=
(x≠0)
?
x
o
y
P(x,y)
1
y
x
2、三角函数的一般定义
三角函数的定义域
三角函数
定义域
sinα
cosα
tanα
R
R
y
x
o
+
-
+
+
+
+
+
-
-
-
-
-
y
x
o
y
x
o
三角函数在各象限的符号
填表:坐标轴上的三角函数
角α
0°
90°
180°
270°
360°
角α的弧度数
sinα
cosα
tanα
例3 求证:当且仅当下列不等式组成立时,角θ为第三角限角.反之也对.
①
②
证明:如果①②式都成立,那么θ为第三象限角.
若sinθ<0,那么θ角的终边可能位于第三或第四象限,也可能位于y轴的非正半轴上
又若tanθ>0,那么θ角的终边可能位于第一或第三象限.
因为①②式都成立,所以θ角的终边只能位于第三象限.于是θ为第三象限角
反过来自己证
可以把求任意角的三角函数值转化为求0到2π(或0°至360°)角的三角函数值.
终边相同的角的同一三角函数值相等
公式一
角α终边每绕原点旋转一周,函数值将重复出现
例4 确定下列三角函数值的符号,然后用计算器验证:
解:(1)因为250°是第___象限角,所以cos250° 0
(2)因为 是第____象限角,所以
(3)因为tan(-672°)=tan(48°-2×360°)=tan48°
而48°是第一象限角,所以 tan(-672°) 0
(4)因为tan3π=tan(π+2π)=tanπ=0
三
<
四
<
>
例5 求下列三角函数值
练 习
课本第15页第5—7题
作业布置
P20—21页第1、6、7题
三角函数线
设任意角?顶点在原点O,始边与x轴非负半轴重合,终边与单位圆相交与点P(x,y),过P作x轴的垂线,垂足为M;过点A(1,0)作单位圆的切线,它与角?的终边或其反向延长线交与点T.
(Ⅰ)
x
y
o
A(1,0)
α的终边
T
P
M
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅱ)
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅳ)
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅱ)
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅲ)
(Ⅰ)
x
y
o
A(1,0)
α的终边
T
P
M
规定:与坐标轴方向一致时为正,与坐标方向相反时为负.
有向线段:规定了方向的线段.
A
B
x
y
o
C
D
有向线段AB:方向A→B;记作
有向线段BA:方向B→A ;记作
有向线段CD:方向C→D,等.
值为正
值为负
当?为第一或二象限角时, y为正,有sin?=y=|MP|,
而当?为第三或四象限角时,y为负,有sin?=y=-|MP|.
探究:能不能去掉绝对值符号,使得线段OM,MP的值与坐标的正负是一致呢?怎样规定?
有向线段的书写: 有向线段的起点字母在前,终点字母在后面.
(Ⅰ)
x
y
o
A(1,0)
α的终边
T
P
M
这样当角 的终边不在坐标轴上时,我们把 , 都看成有向线段。由正弦、余弦、正切函数的定义有:
x
y
o
A(1,0)
α的终边
T
P
M
(Ⅲ)
三角函数线定义
有向线段MP、OM、AT分别称为正弦线、余弦线、正切线.
统称为三角函数线.(它是三角函数值的一种几何表示法)
当角 的终边在 轴上时,正弦线、正切线分别
变成一个点;此时角 的正弦值和正切值都为0.
当角 的终边在 轴上时,余弦线变成一个点,正切线不存在,此时角 的正切值不存在.
说明:
① 三条有向线段的位置:正弦线为?的终边与单位圆的交点到x轴的垂直线段;余弦线在x轴上;正切线在过单位圆与x轴正方向的交点的切线上,三条有向线段中两条在单位圆内,一条在单位圆外。
② 三条有向线段的正负:三条有向线段凡与x轴或y轴同向的为正值,与x轴或y轴反向的为负值。
课堂小结
1.三角函数线是三角函数的一种几何表示,即用有向线段表示三角函数值,是今后进一步研究三角函数图象的有效工具.
2.三角函数线:用有向线段的数量来表示。
O
x
y
P
M
A
T
3.终边相同的角的同一三角函数值相等.
