高中数学人教A版必修4课件-1.3三角函数的诱导公式 2课时(22张PPT)
文档属性
| 名称 | 高中数学人教A版必修4课件-1.3三角函数的诱导公式 2课时(22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 21:46:02 | ||
图片预览








文档简介
1.3 三角函数的诱导公式(1)
复习引入
1.在单位圆里,角α的正弦、余弦、正切是怎样 定义的?
α的终边
P(x,y)
O
x
y
公式一:
( )
α的终边
x
y
o
π+α的终边
思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?
关于原点对称
α的终边
x
y
o
π+α的终边
P(x,y)
Q(-x,-y)
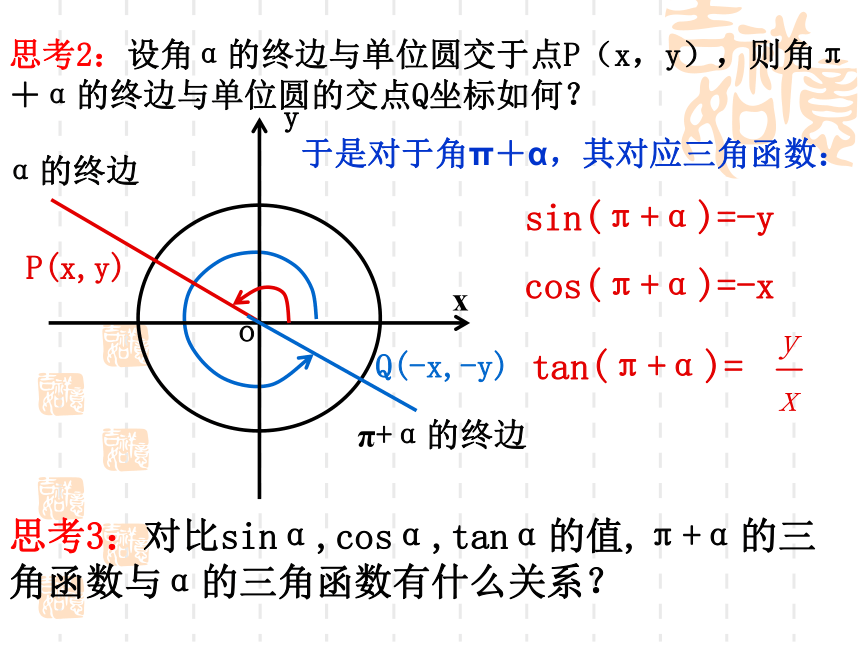
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点Q坐标如何?
sin(π+α)=-y
cos(π+α)=-x
tan(π+α)=
思考3:对比sinα,cosα,tanα的值,π+α的三角函数与α的三角函数有什么关系?
于是对于角π+α,其对应三角函数:
公式二:
同理,我们有:
公式三:
公式四:
公式一:
公式二:
公式三:
公式四:
简记为:函数名不变,符号看象限
的三角函数值,等于 的同名三角函数值前面加上把 看作锐角时原函数值的符号。
公式一、二、三、四、都叫做诱导公式.
例如:
解题一般步骤
负角
正角
0~2π
0~π
锐角
例1.求下列三角函数值
例题分析
例2.化简
练习:
P27 第1、2、3题
作业布置
课本P29 A组第1、2(1)(6) 题
(写出具体的解题步骤)
1.3 三角函数的诱导公式(2)
复习回顾
四个诱导公式:
公式一:
公式二:
公式三:
公式四:
注意:
看成锐角,原函数值的符号
诱导公式记忆口诀:
函数名不变
符号看象限
公式一至公式四
请同学们思考回答点 关于直线 对称的点 的坐标是什么?
已知任意角 的终边与单位圆相交于点 ,
y
x
0
-1
1
P1(x,y)
P2(y,x)
y
x
0
-1
1
P1(x,y)
P2(y,x)
y
x
0
1
-1
-1
1
P(x,y)
P′(y,x)
注意:
看成锐角,原函数值的符号
诱导公式记忆口诀:
函数名不变 符号看象限
公式一至公式四:
公式五和公式六:
正余(弦)互换 符号看象限
解:
例3 证明:
例题讲解
解:
例4 化简:
练习:
P28 第7题
作业布置
课本P29 A组第3
B组第1、2(1)(3) 题
(写出具体的解题步骤)
复习引入
1.在单位圆里,角α的正弦、余弦、正切是怎样 定义的?
α的终边
P(x,y)
O
x
y
公式一:
( )
α的终边
x
y
o
π+α的终边
思考1:对于任意给定的一个角α,角π+α的终边与角α的终边有什么关系?
关于原点对称
α的终边
x
y
o
π+α的终边
P(x,y)
Q(-x,-y)
思考2:设角α的终边与单位圆交于点P(x,y),则角π+α的终边与单位圆的交点Q坐标如何?
sin(π+α)=-y
cos(π+α)=-x
tan(π+α)=
思考3:对比sinα,cosα,tanα的值,π+α的三角函数与α的三角函数有什么关系?
于是对于角π+α,其对应三角函数:
公式二:
同理,我们有:
公式三:
公式四:
公式一:
公式二:
公式三:
公式四:
简记为:函数名不变,符号看象限
的三角函数值,等于 的同名三角函数值前面加上把 看作锐角时原函数值的符号。
公式一、二、三、四、都叫做诱导公式.
例如:
解题一般步骤
负角
正角
0~2π
0~π
锐角
例1.求下列三角函数值
例题分析
例2.化简
练习:
P27 第1、2、3题
作业布置
课本P29 A组第1、2(1)(6) 题
(写出具体的解题步骤)
1.3 三角函数的诱导公式(2)
复习回顾
四个诱导公式:
公式一:
公式二:
公式三:
公式四:
注意:
看成锐角,原函数值的符号
诱导公式记忆口诀:
函数名不变
符号看象限
公式一至公式四
请同学们思考回答点 关于直线 对称的点 的坐标是什么?
已知任意角 的终边与单位圆相交于点 ,
y
x
0
-1
1
P1(x,y)
P2(y,x)
y
x
0
-1
1
P1(x,y)
P2(y,x)
y
x
0
1
-1
-1
1
P(x,y)
P′(y,x)
注意:
看成锐角,原函数值的符号
诱导公式记忆口诀:
函数名不变 符号看象限
公式一至公式四:
公式五和公式六:
正余(弦)互换 符号看象限
解:
例3 证明:
例题讲解
解:
例4 化简:
练习:
P28 第7题
作业布置
课本P29 A组第3
B组第1、2(1)(3) 题
(写出具体的解题步骤)
