高中数学人教A版必修4课件-2.2.2 向量减法运算及其几何意义(共14张PPT)
文档属性
| 名称 | 高中数学人教A版必修4课件-2.2.2 向量减法运算及其几何意义(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 630.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 00:00:00 | ||
图片预览


文档简介
2.2.2 向量减法运算及其几何意义
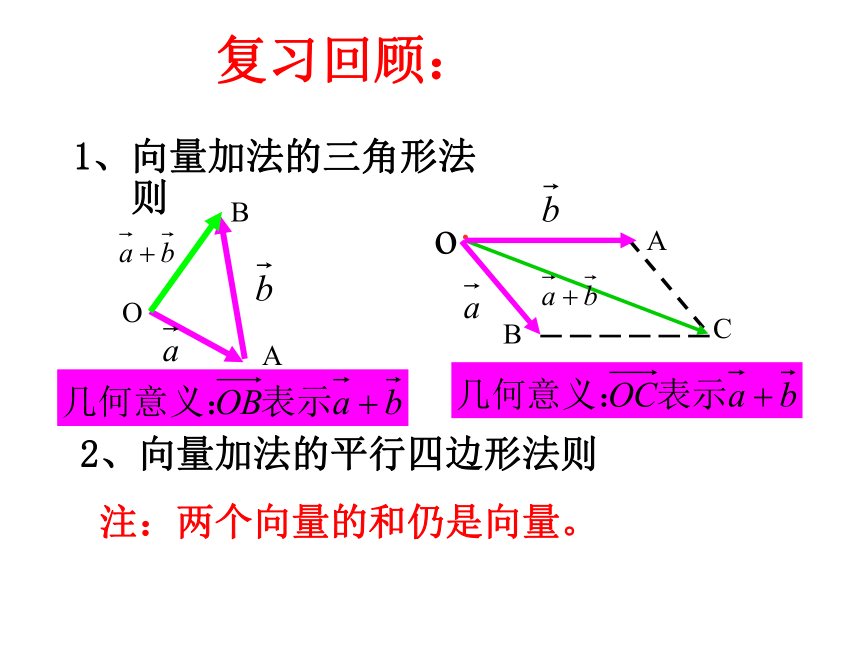
1、向量加法的三角形法则
2、向量加法的平行四边形法则
注:两个向量的和仍是向量。
复习回顾:
B
A
O
o·
A
B
C
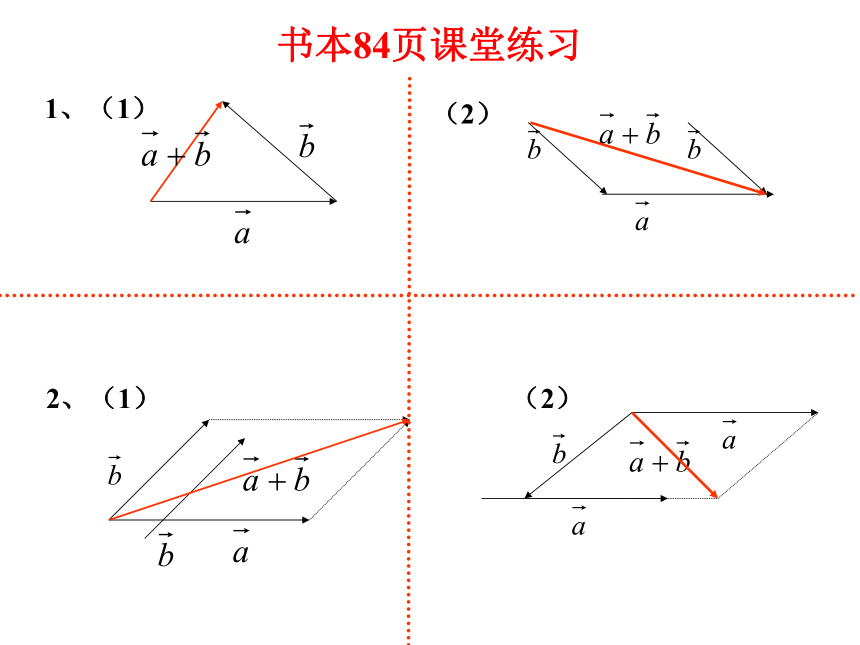
1、(1)
(2)
书本84页课堂练习
2、(1)
(2)
北京
广州
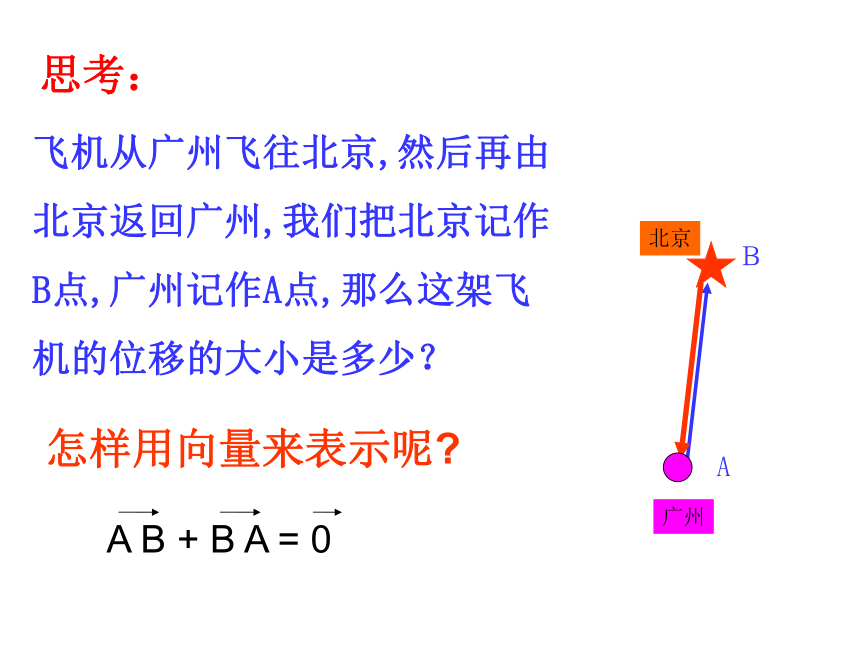
飞机从广州飞往北京,然后再由北京返回广州,我们把北京记作B点,广州记作A点,那么这架飞机的位移的大小是多少?
A
B
怎样用向量来表示呢?
A B + B A = 0
思考:
“相反向量”的定义:
与a长度相同、方向相反的向量,记作 ?a
注:1.零向量的相反向量仍是零向量;
2.任一向量与其相反向量的和是零向量;
O
B
A
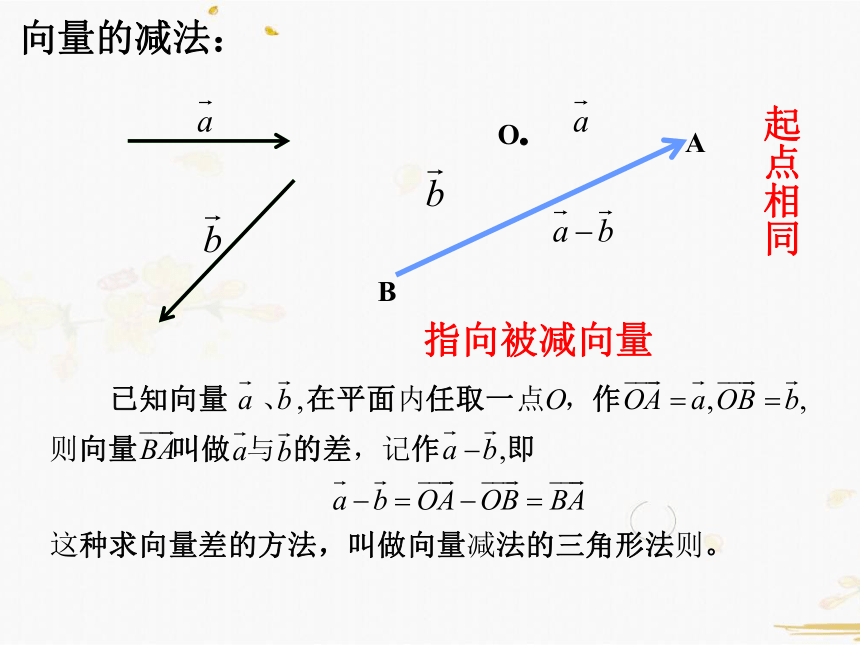
向量的减法:
起点相同
指向被减向量
O
A
B
①将两向量平移,使它们有相同的起点.
②连接两向量的终点.
③箭头的方向是指向“被减向量”的终点.
解:有向量加法的平行四边形法则,
得
由向量的减法可得,
重要结论:
试化简
解
课堂练习:
P87 第1、2题
P91 第4(4)(5)(6)(7)题
1.掌握向量减法概念并知道向量的减法的定义是建立在向量加法的基础上的;
2.会作两个向量的差向量;
3.能够结合图形进行向量的计算以及用两个向量表示其他向量.
小结:
1、向量加法的三角形法则
2、向量加法的平行四边形法则
注:两个向量的和仍是向量。
复习回顾:
B
A
O
o·
A
B
C
1、(1)
(2)
书本84页课堂练习
2、(1)
(2)
北京
广州
飞机从广州飞往北京,然后再由北京返回广州,我们把北京记作B点,广州记作A点,那么这架飞机的位移的大小是多少?
A
B
怎样用向量来表示呢?
A B + B A = 0
思考:
“相反向量”的定义:
与a长度相同、方向相反的向量,记作 ?a
注:1.零向量的相反向量仍是零向量;
2.任一向量与其相反向量的和是零向量;
O
B
A
向量的减法:
起点相同
指向被减向量
O
A
B
①将两向量平移,使它们有相同的起点.
②连接两向量的终点.
③箭头的方向是指向“被减向量”的终点.
解:有向量加法的平行四边形法则,
得
由向量的减法可得,
重要结论:
试化简
解
课堂练习:
P87 第1、2题
P91 第4(4)(5)(6)(7)题
1.掌握向量减法概念并知道向量的减法的定义是建立在向量加法的基础上的;
2.会作两个向量的差向量;
3.能够结合图形进行向量的计算以及用两个向量表示其他向量.
小结:
