高中数学人教A版必修4课件-2.3.1平面向量基本定理(12张PPT)
文档属性
| 名称 | 高中数学人教A版必修4课件-2.3.1平面向量基本定理(12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 08:25:34 | ||
图片预览


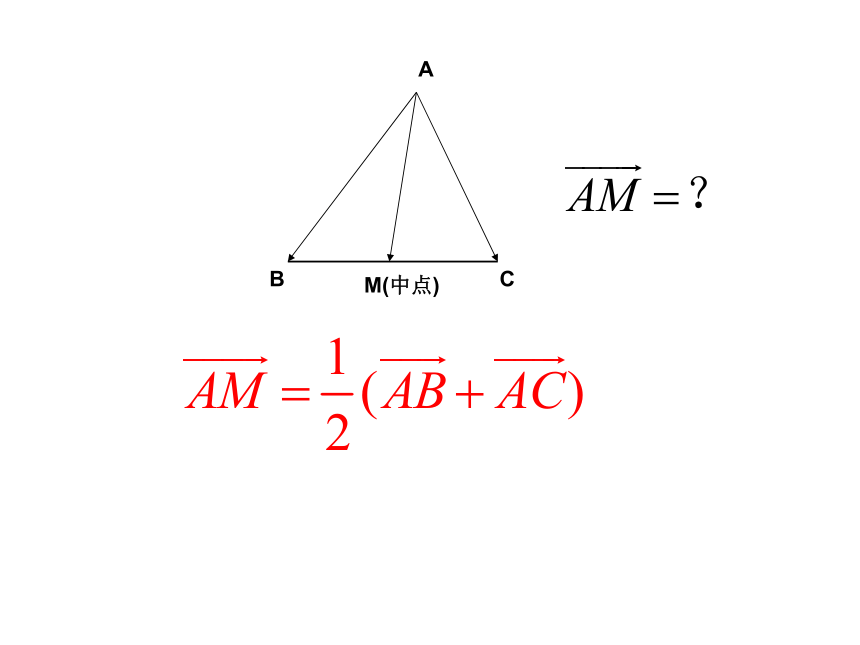

文档简介
2.3.1 平面向量基本定理
复 习
1、实数与向量的积
2、两个向量的和(差)的求法
平行四边形法则
三角形法则
3、两个向量共线定理
向量b与非零向量a共线
有且只有一个实数λ,使得 b =λa
B
A
C
M(中点)
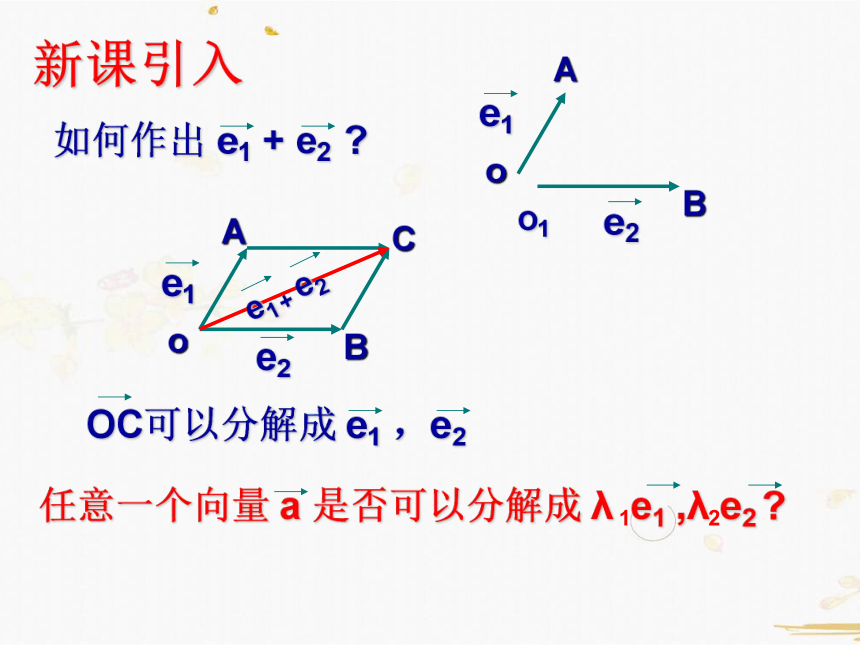
新课引入
如何作出 e1 + e2 ?
e1
o
A
o1
B
e2
o
A
e1
B
e2
C
e1
e2
+
OC可以分解成 e1 ,e2
任意一个向量 a 是否可以分解成 λ 1e1 ,λ2e2 ?
e1
o
A
o1
B
a
o2
C
e2
o
A
B
C
N
M
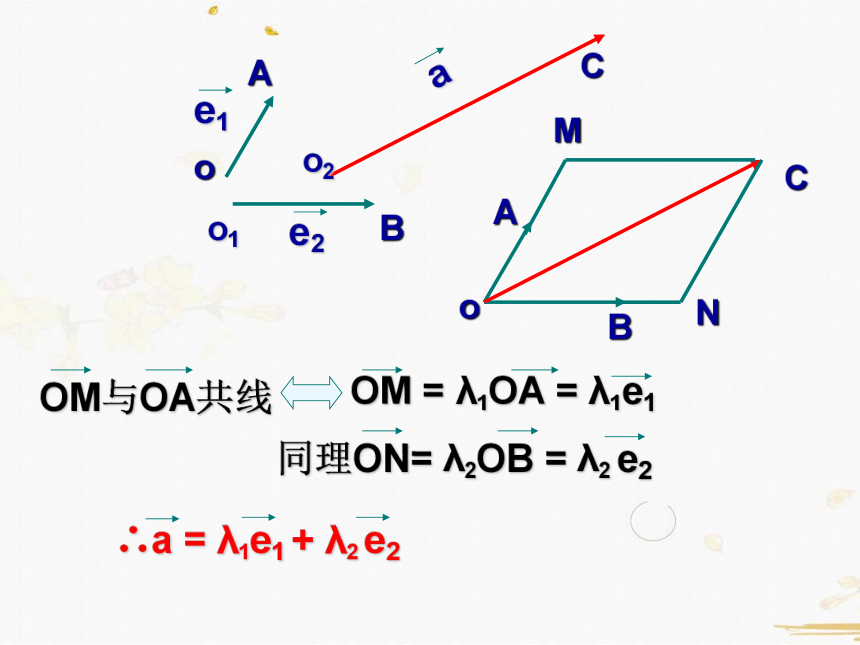
OM与OA共线
OM = λ1OA = λ1e1
同理ON= λ2OB = λ2 e2
∴a = λ1e1 + λ2 e2
平面向量基本定理:
如果 e1 , e2 是同一平面内的两个不共线向量,那么对于这个平面内的任意一个向量 a ,有且只有一对实数λ1 , λ2 使
其中不共线向量 e1 ,e2 叫做表示这个平面内的所有向量的一组基底。
a = λ1 e1 + λ2 e2
平面向量基本定理的拓展
? 探究1:
一组平面向量的基底有多少对?
无数对
? 探究2:
若基底选择不同,则表示同一向量的
实数
是否相同?
可以相同,也可不同
O
F
C
E
A
E
B
N
D
O
A
B
C
两个向量的夹角
(1)定义
已知两个 向量a和b,作 =a,
=b,则∠AOB=θ叫做向量a
与b的夹角.
(2)范围
向量夹角θ的范围是 ,a与b同向时,
夹角θ= ;a与b反向时,夹角θ= .
非零
0°≤θ≤180°
180°
0°
(3)向量垂直
如果向量a与b的夹角是 ,则a与b垂直,记作 .
90°
a⊥b
课堂小结:
1)平面向量基本定理内容
定理的拓展性
2)对定理的理解与拓展
实数对
的存在性和唯一性
基底的不唯一性
3)平面向量基本定理的应用
练习:
B
A
C
D
则下面的四组向量中不能作为一组基底的是
是平面内所有向量的一组基底,
2、若
(B)
B
O
P
A
复 习
1、实数与向量的积
2、两个向量的和(差)的求法
平行四边形法则
三角形法则
3、两个向量共线定理
向量b与非零向量a共线
有且只有一个实数λ,使得 b =λa
B
A
C
M(中点)
新课引入
如何作出 e1 + e2 ?
e1
o
A
o1
B
e2
o
A
e1
B
e2
C
e1
e2
+
OC可以分解成 e1 ,e2
任意一个向量 a 是否可以分解成 λ 1e1 ,λ2e2 ?
e1
o
A
o1
B
a
o2
C
e2
o
A
B
C
N
M
OM与OA共线
OM = λ1OA = λ1e1
同理ON= λ2OB = λ2 e2
∴a = λ1e1 + λ2 e2
平面向量基本定理:
如果 e1 , e2 是同一平面内的两个不共线向量,那么对于这个平面内的任意一个向量 a ,有且只有一对实数λ1 , λ2 使
其中不共线向量 e1 ,e2 叫做表示这个平面内的所有向量的一组基底。
a = λ1 e1 + λ2 e2
平面向量基本定理的拓展
? 探究1:
一组平面向量的基底有多少对?
无数对
? 探究2:
若基底选择不同,则表示同一向量的
实数
是否相同?
可以相同,也可不同
O
F
C
E
A
E
B
N
D
O
A
B
C
两个向量的夹角
(1)定义
已知两个 向量a和b,作 =a,
=b,则∠AOB=θ叫做向量a
与b的夹角.
(2)范围
向量夹角θ的范围是 ,a与b同向时,
夹角θ= ;a与b反向时,夹角θ= .
非零
0°≤θ≤180°
180°
0°
(3)向量垂直
如果向量a与b的夹角是 ,则a与b垂直,记作 .
90°
a⊥b
课堂小结:
1)平面向量基本定理内容
定理的拓展性
2)对定理的理解与拓展
实数对
的存在性和唯一性
基底的不唯一性
3)平面向量基本定理的应用
练习:
B
A
C
D
则下面的四组向量中不能作为一组基底的是
是平面内所有向量的一组基底,
2、若
(B)
B
O
P
A
