高中数学人教A版必修4课件-期末复习(35张PPT)
文档属性
| 名称 | 高中数学人教A版必修4课件-期末复习(35张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 09:02:52 | ||
图片预览








文档简介
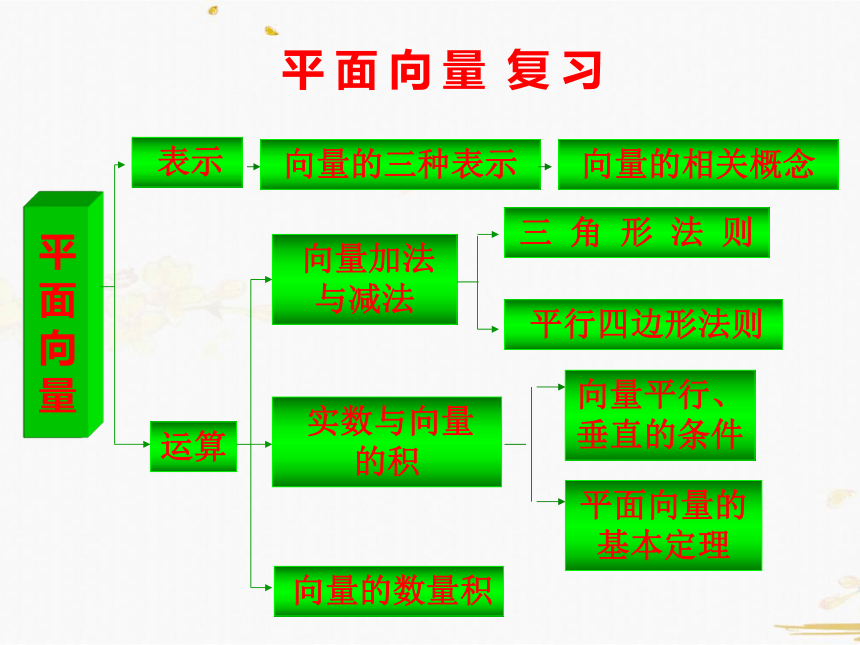
平面向量复
面
向
量
复
面
向
量
表示
运算
实数与向量
的积
向量加法与减法
向量的数量积
平行四边形法则
向量平行、垂直的条件
平面向量的基本定理
三
角
形
法
则
向量的三种表示
向量的相关概念
向量定义:
既有大小又有方向的量叫向量。
重要概念:
(1)零向量:
长度为0的向量,记作0.
(2)单位向量:
长度为1个单位长度的向量.
(3)平行向量:
也叫共线向量,方向相同或相反
的非零向量.
(4)相等向量:
长度相等且方向相同的向量.
(5)相反向量:
长度相等且方向相反的向量.
几何表示
:
有向线段
向量的表示
字母表示
坐标表示
:
(x,y)
若
A(x1,y1),
B(x2,y2)
则
AB
=
(x2
-
x1
,
y2
-
y1)
向量的模(长度)
1.
设
a
=
(
x
,
y
),
则
2.
若表示向量
a
的起点和终点的坐标分别
为A(x1,y1)、B
(x2,y2)
,则
平
面
向
量
复
习
1.向量的加法运算
A
B
C
AB+BC=
三角形法则
O
A
B
C
OA+OB=
平行四边形法则
坐标运算:
则a
+
b
=
重要结论:AB+BC+CA=
0
设
a
=
(x1,
y1),
b
=
(x2,
y2)
(
x1
+
x2
,
y1
+
y2
)
AC
OC
平
面
向
量
复
习
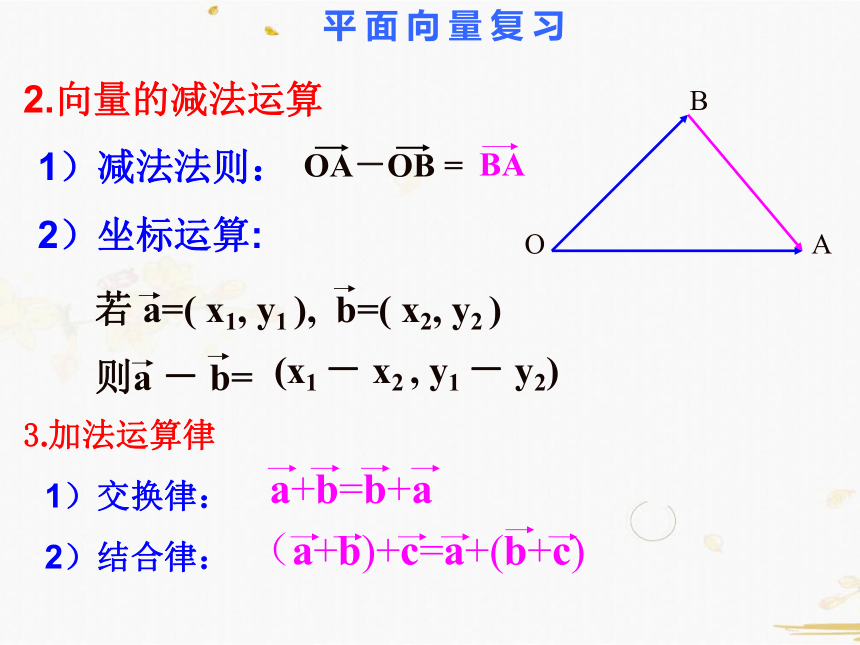
2.向量的减法运算
1)减法法则:
O
A
B
2)坐标运算:
若
a=(
x1,
y1
),
b=(
x2,
y2
)
则a
-
b=
3.加法运算律
a+b=b+a
(a+b)+c=a+(b+c)
1)交换律:
2)结合律:
BA
(x1
-
x2
,
y1
-
y2)
OA-OB
=
平
面
向
量
复
习
实数λ与向量
a
的积
定义:
坐标运算:
其实质就是向量的伸长或缩短!
λa是一个
向量.
它的长度
|λa|
=
|λ|
|a|;
它的方向
(1)
当λ≥0时,λa
的方向
与a方向相同;
(2)
当λ<0时,λa
的方向
与a方向相反.
若a
=
(x
,
y),
则λa
=
λ
(x
,
y)
=
(λ
x
,
λ
y)
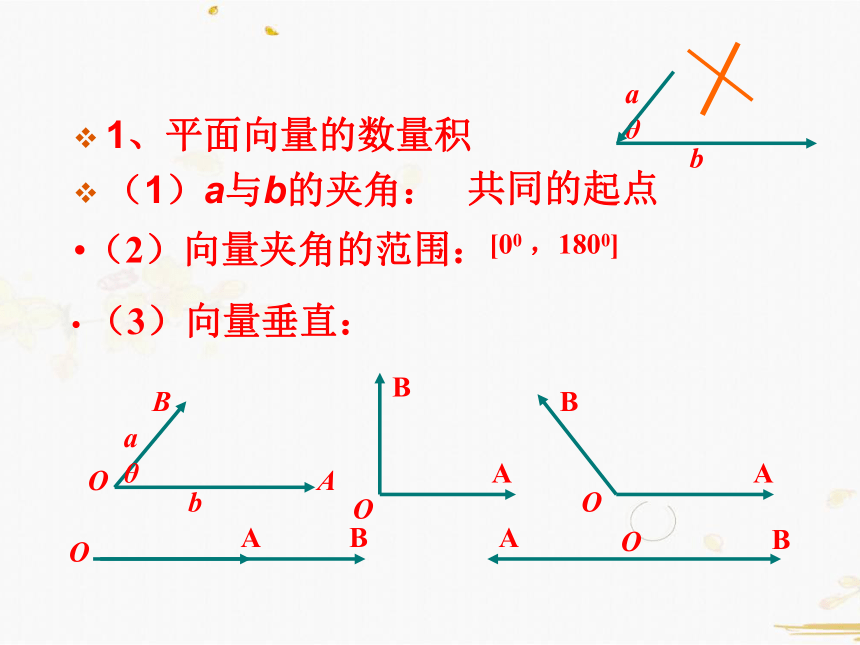
1、平面向量的数量积
(1)a与b的夹角:
(2)向量夹角的范围:
(3)向量垂直:
[00
,1800]
a
b
θ
共同的起点
a
O
A
B
b
θ
O
A
B
O
A
B
O
A
B
O
A
B
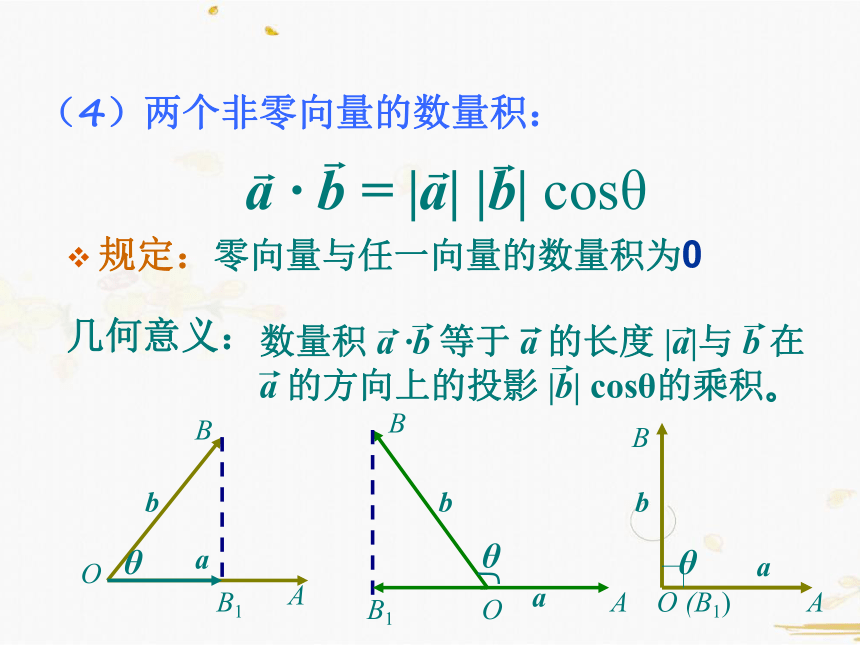
(4)两个非零向量的数量积:
规定:零向量与任一向量的数量积为0
a
·
b
=
|a|
|b|
cosθ
几何意义:
数量积
a
·b
等于
a
的长度
|a|与
b
在
a
的方向上的投影
|b|
cosθ的乘积。
A
a
b
θ
B
B1
O
B
A
θ
b
B1
a
O
θ
B
b
(B1)
A
a
O
5、数量积的运算律:
⑴交换律:
⑵对数乘的结合律:
⑶分配律:
注意:
数量积不满足结合律
平面向量数量积的重要性质
(1)e
·
a
=
a
·
e
=|
a
|
cosθ
(2)a
⊥
b的条件是
a
·
b
=0
(3)
当
a与b同向时,
a
·
b
=
|a
|
|
b
|
;
当
a
与b
反向时,a
·
b
=
-
|a
|
|
b
|
特别地:a
·
a=|
a
|
2
或
|
a
|
=
(4)cosθ=
(5)|
a·b
|
≤
|
a
|
|
b
|
a,b为非零向量,e为单位向量
二、平面向量之间关系
向量平行(共线)条件的两种形式:
向量垂直条件的两种形式:
(3)两个向量相等的条件是两个向量的
坐标相等.
即:
那么
三、平面向量的基本定理
如果
是同一平面内的两个不共线
向量,那么对于这一平面内的任一向
量
,有且只有一对实数
使
三角函数
1、任意角:正角、负角、零角。
2
、终边与
角a相同的角的集合:
S={β|β=α+k·360°,k∈Z}
3、弧度制与角度制的相互转化。
4、扇形的面积公式。
5、任意角的三角函数的定义、在各象限的符号、坐标轴上的值。
6、同角三角函数的基本关系。
7、三角函数的诱导公式(公式一至公式六)。
函数
y=sinx
y=cosx
图形
定义域
值域
最值
单调性
奇偶性
周期
1
-1
时,
时,
时,
时,
增函数
减函数
增函数
减函数
1
-1
奇函数
偶函数
8、正弦余弦函数的图象及性质:
y
x
1
-1
?/2
-?/2
?
3?/2
-3?/2
-?
0
定义域
值域
周期性
奇偶性
单调性
R
T=
?
奇函数
函数
y=tanx
增区间
t
t+?
t-?
9、正切函数的图象与性质
先平移后伸缩的方法
y=sin(?
x+
?
)
的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0y=Asin(?x+
?
)的图象
函数
y=sinx
y=sin
?
x
的图象
(1)横坐标缩短(?
>1)或伸长(0原来的
倍,纵坐标不变
(2)向左(?
>0)或向右(?
<0)
平移|
|个单位
先伸缩后平移
的一般规律:
代点法
求φ常用的两种方法:
(注:X1,X2是相邻的最高最低点的横坐标
或者是函数相邻的两个零点
)
集合与函数
集合
集合含义与表示
集合间关系
集合基本运算
列举法
描述法
图示法
子集
真子集
补集
并集
交集
一、知识结构
知识结构
概念
三要素
图象
性质
指数函数
应用
大小比较
方程解的个数
不等式的解
实际应用
对数函数
函数
函数
定义域
奇偶性
图象
值域
单调性
二次函数
指数函数
对数函数
函数的复习主要抓住两条主线
1、函数的概念及其有关性质。
2、几种初等函数的具体性质。
反比例函数
反比例函数
1、定义域
.
2、值域
4、图象
k>0
k<0
3、单调性
二次函数
1、定义域
.
2、值域
3、单调性
4、图象
a>0
a<0
指数函数
1、定义域
.
2、值域
3、单调性
4、图象
a>1
0在(
)递增
在(
)递减
y
x
o
1
y
x
o
1
(0,+∞)
对数函数
1、定义域
.
2、值域
3、单调性
4、图象
a>1
0在(0,
)递增
在(0,
)递减
y
x
o
y
x
o
1
1
(0,+∞)
在同一平面直角坐标系内作出幂函数y=x,y=x2,y=x3,y=x1/2,y=x-1的图象:
(-∞,0)减
(-∞,0]减
(1,1)
(1,1)
(1,1)
(1,1)
(1,1)
公共点
(0,+∞)减
增
增
[0,+∞)增
增
单调性
奇
非奇非偶
奇
偶
奇
奇偶性
{y|y≠0}
[0,+∞)
R
[0,+∞)
R
值域
{x|x≠0}
[0,+∞)
R
R
R
定义域
y=x-1
y=x3
y=x2
y=x
函数
性质
幂函数的性质
2
1
x
y
=
使函数有意义的x的取值范围。
求定义域的主要依据
1、分式的分母不为零.
2、偶次方根的被开方数不小于零.
3、零次幂的底数不为零.
4、对数函数的真数大于零.
5、指、对数函数的底数大于零且不为1.
6、实际问题中函数的定义域
求函数解析式的方法:
待定系数法、换元法、配凑法
求值域的一些方法:
1、图像法,2
、
配方法,3、逆求法,
4、分离常数法,5、换元法,6单调性法。
一、函数的奇偶性定义
前提条件:定义域关于定义域对称。
1、奇函数
f
(-x)=
-
f
(x)
或
f
(-x)+f
(x)
=
0
2、偶函数
f
(-x)
=
f
(x)
或f
(-x)
-
f
(x)
=
0
二、奇函数、偶函数的图象特点
1、奇函数的图象关于原点成中心对称图形。
2、偶函数的图象关于y轴成轴对称图形。
1、方程的根与零点
函数y=f(x)有零点
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数的应用知识网络
2、函数模型及其应用
掌握常见的函数模型:
一次函数模型、二次函数模型(最值问题)
课本P102
例3
、P104例5
面
向
量
复
面
向
量
表示
运算
实数与向量
的积
向量加法与减法
向量的数量积
平行四边形法则
向量平行、垂直的条件
平面向量的基本定理
三
角
形
法
则
向量的三种表示
向量的相关概念
向量定义:
既有大小又有方向的量叫向量。
重要概念:
(1)零向量:
长度为0的向量,记作0.
(2)单位向量:
长度为1个单位长度的向量.
(3)平行向量:
也叫共线向量,方向相同或相反
的非零向量.
(4)相等向量:
长度相等且方向相同的向量.
(5)相反向量:
长度相等且方向相反的向量.
几何表示
:
有向线段
向量的表示
字母表示
坐标表示
:
(x,y)
若
A(x1,y1),
B(x2,y2)
则
AB
=
(x2
-
x1
,
y2
-
y1)
向量的模(长度)
1.
设
a
=
(
x
,
y
),
则
2.
若表示向量
a
的起点和终点的坐标分别
为A(x1,y1)、B
(x2,y2)
,则
平
面
向
量
复
习
1.向量的加法运算
A
B
C
AB+BC=
三角形法则
O
A
B
C
OA+OB=
平行四边形法则
坐标运算:
则a
+
b
=
重要结论:AB+BC+CA=
0
设
a
=
(x1,
y1),
b
=
(x2,
y2)
(
x1
+
x2
,
y1
+
y2
)
AC
OC
平
面
向
量
复
习
2.向量的减法运算
1)减法法则:
O
A
B
2)坐标运算:
若
a=(
x1,
y1
),
b=(
x2,
y2
)
则a
-
b=
3.加法运算律
a+b=b+a
(a+b)+c=a+(b+c)
1)交换律:
2)结合律:
BA
(x1
-
x2
,
y1
-
y2)
OA-OB
=
平
面
向
量
复
习
实数λ与向量
a
的积
定义:
坐标运算:
其实质就是向量的伸长或缩短!
λa是一个
向量.
它的长度
|λa|
=
|λ|
|a|;
它的方向
(1)
当λ≥0时,λa
的方向
与a方向相同;
(2)
当λ<0时,λa
的方向
与a方向相反.
若a
=
(x
,
y),
则λa
=
λ
(x
,
y)
=
(λ
x
,
λ
y)
1、平面向量的数量积
(1)a与b的夹角:
(2)向量夹角的范围:
(3)向量垂直:
[00
,1800]
a
b
θ
共同的起点
a
O
A
B
b
θ
O
A
B
O
A
B
O
A
B
O
A
B
(4)两个非零向量的数量积:
规定:零向量与任一向量的数量积为0
a
·
b
=
|a|
|b|
cosθ
几何意义:
数量积
a
·b
等于
a
的长度
|a|与
b
在
a
的方向上的投影
|b|
cosθ的乘积。
A
a
b
θ
B
B1
O
B
A
θ
b
B1
a
O
θ
B
b
(B1)
A
a
O
5、数量积的运算律:
⑴交换律:
⑵对数乘的结合律:
⑶分配律:
注意:
数量积不满足结合律
平面向量数量积的重要性质
(1)e
·
a
=
a
·
e
=|
a
|
cosθ
(2)a
⊥
b的条件是
a
·
b
=0
(3)
当
a与b同向时,
a
·
b
=
|a
|
|
b
|
;
当
a
与b
反向时,a
·
b
=
-
|a
|
|
b
|
特别地:a
·
a=|
a
|
2
或
|
a
|
=
(4)cosθ=
(5)|
a·b
|
≤
|
a
|
|
b
|
a,b为非零向量,e为单位向量
二、平面向量之间关系
向量平行(共线)条件的两种形式:
向量垂直条件的两种形式:
(3)两个向量相等的条件是两个向量的
坐标相等.
即:
那么
三、平面向量的基本定理
如果
是同一平面内的两个不共线
向量,那么对于这一平面内的任一向
量
,有且只有一对实数
使
三角函数
1、任意角:正角、负角、零角。
2
、终边与
角a相同的角的集合:
S={β|β=α+k·360°,k∈Z}
3、弧度制与角度制的相互转化。
4、扇形的面积公式。
5、任意角的三角函数的定义、在各象限的符号、坐标轴上的值。
6、同角三角函数的基本关系。
7、三角函数的诱导公式(公式一至公式六)。
函数
y=sinx
y=cosx
图形
定义域
值域
最值
单调性
奇偶性
周期
1
-1
时,
时,
时,
时,
增函数
减函数
增函数
减函数
1
-1
奇函数
偶函数
8、正弦余弦函数的图象及性质:
y
x
1
-1
?/2
-?/2
?
3?/2
-3?/2
-?
0
定义域
值域
周期性
奇偶性
单调性
R
T=
?
奇函数
函数
y=tanx
增区间
t
t+?
t-?
9、正切函数的图象与性质
先平移后伸缩的方法
y=sin(?
x+
?
)
的图象
(3)横坐标不变,纵坐标伸长(A>1)
或缩短(0
?
)的图象
函数
y=sinx
y=sin
?
x
的图象
(1)横坐标缩短(?
>1)或伸长(0原来的
倍,纵坐标不变
(2)向左(?
>0)或向右(?
<0)
平移|
|个单位
先伸缩后平移
的一般规律:
代点法
求φ常用的两种方法:
(注:X1,X2是相邻的最高最低点的横坐标
或者是函数相邻的两个零点
)
集合与函数
集合
集合含义与表示
集合间关系
集合基本运算
列举法
描述法
图示法
子集
真子集
补集
并集
交集
一、知识结构
知识结构
概念
三要素
图象
性质
指数函数
应用
大小比较
方程解的个数
不等式的解
实际应用
对数函数
函数
函数
定义域
奇偶性
图象
值域
单调性
二次函数
指数函数
对数函数
函数的复习主要抓住两条主线
1、函数的概念及其有关性质。
2、几种初等函数的具体性质。
反比例函数
反比例函数
1、定义域
.
2、值域
4、图象
k>0
k<0
3、单调性
二次函数
1、定义域
.
2、值域
3、单调性
4、图象
a>0
a<0
指数函数
1、定义域
.
2、值域
3、单调性
4、图象
a>1
0
)递增
在(
)递减
y
x
o
1
y
x
o
1
(0,+∞)
对数函数
1、定义域
.
2、值域
3、单调性
4、图象
a>1
0
)递增
在(0,
)递减
y
x
o
y
x
o
1
1
(0,+∞)
在同一平面直角坐标系内作出幂函数y=x,y=x2,y=x3,y=x1/2,y=x-1的图象:
(-∞,0)减
(-∞,0]减
(1,1)
(1,1)
(1,1)
(1,1)
(1,1)
公共点
(0,+∞)减
增
增
[0,+∞)增
增
单调性
奇
非奇非偶
奇
偶
奇
奇偶性
{y|y≠0}
[0,+∞)
R
[0,+∞)
R
值域
{x|x≠0}
[0,+∞)
R
R
R
定义域
y=x-1
y=x3
y=x2
y=x
函数
性质
幂函数的性质
2
1
x
y
=
使函数有意义的x的取值范围。
求定义域的主要依据
1、分式的分母不为零.
2、偶次方根的被开方数不小于零.
3、零次幂的底数不为零.
4、对数函数的真数大于零.
5、指、对数函数的底数大于零且不为1.
6、实际问题中函数的定义域
求函数解析式的方法:
待定系数法、换元法、配凑法
求值域的一些方法:
1、图像法,2
、
配方法,3、逆求法,
4、分离常数法,5、换元法,6单调性法。
一、函数的奇偶性定义
前提条件:定义域关于定义域对称。
1、奇函数
f
(-x)=
-
f
(x)
或
f
(-x)+f
(x)
=
0
2、偶函数
f
(-x)
=
f
(x)
或f
(-x)
-
f
(x)
=
0
二、奇函数、偶函数的图象特点
1、奇函数的图象关于原点成中心对称图形。
2、偶函数的图象关于y轴成轴对称图形。
1、方程的根与零点
函数y=f(x)有零点
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数的应用知识网络
2、函数模型及其应用
掌握常见的函数模型:
一次函数模型、二次函数模型(最值问题)
课本P102
例3
、P104例5
