七年级数学平行线的判定
图片预览


文档简介
(共17张PPT)
平行线的判定方法有哪三种?它
们是先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
问题
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
问题
A
B
P
C
D
E
F
2
1
A
B
C
D
E
F
2
1
E’
F’
3
4
5
6
8
7
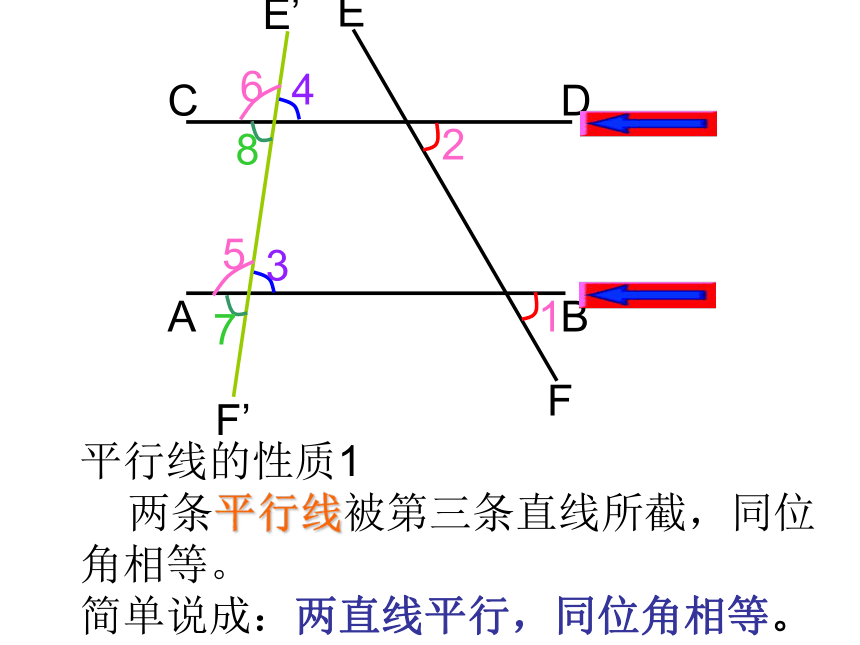
平行线的性质1
两条平行线被第三条直线所截,同位
角相等。
简单说成:两直线平行,同位角相等。
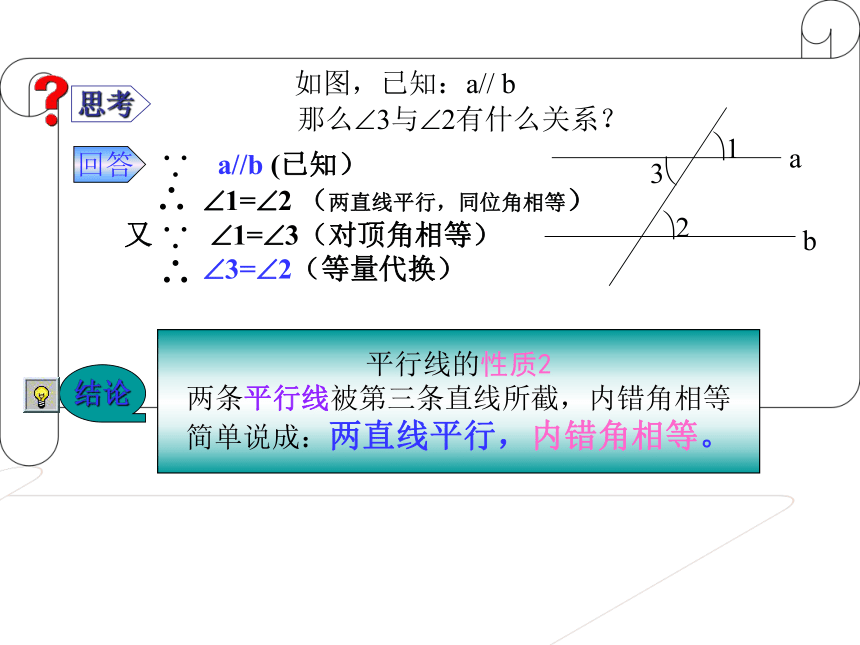
a//b (已知)
1= 2 (两直线平行,同位角相等)
又 1= 3(对顶角相等)
3= 2(等量代换)
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 3与 2有什么关系?
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
结论
c
2
3
1
b
a
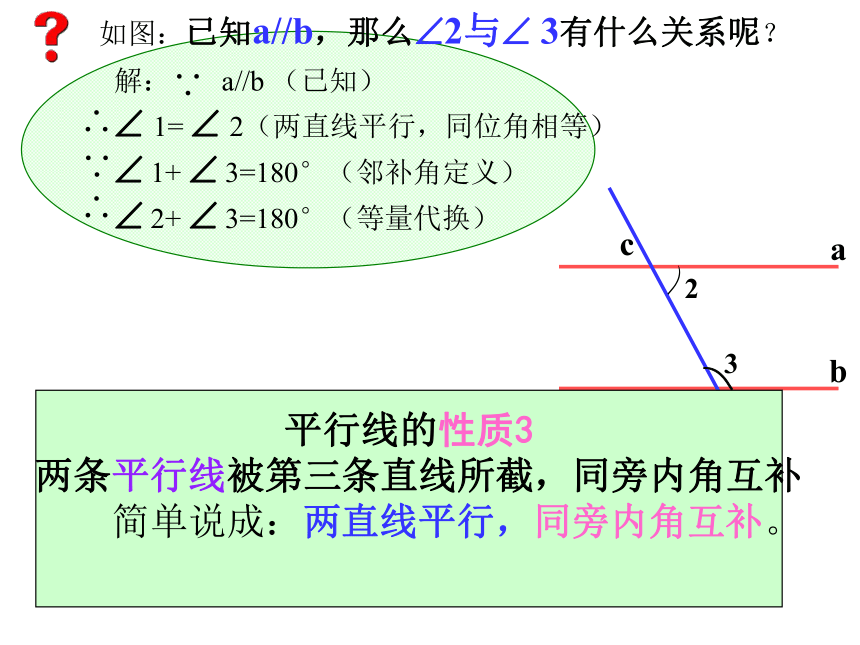
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
如图:已知a//b,那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放
复习回顾
新课学习
巩固练习
课堂小结
c
d
a
b
3
4
2
1
例2 如图所示 ∠1 =∠2
说明 : ∠3 =∠4
说明:∵ ∠1 =∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行,内错角相等)
说明:因为 AD∥BC,( )
§5.3 平行线的性质(一)
所以 ∠A+∠AEF=180°,
因为 ∠AEF=∠B,
所以 ∠A+∠B=180°.
所以 AD∥EF.
已知
( )
( )
( )
( )
两直线平行,同旁内角互补
已知
等量代换
同旁内角互补,两直线平行
例3 如图所示.
已知:AD∥BC,
∠AEF=∠B,
说明:AD∥EF.
平行线的“判定”与“性质”有什么不同
比一比
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
练习1
如图,已知直线a∥b,
∠3=131°,求∠ 1、∠2的度数。
解(1)∵∠1=∠3 (对顶角相等)
且∠3=131°(已知)
∴∠1 =131°
(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又 ∵ ∠1=131°
∴ ∠2=49°。
解:∵AD//BC (已知)
∴ A + B=180°
(两直线平行,同旁内角互补)
∴ B= 180 °- A =180 ° -115 °=65 °
∵AD//BC (已知)
∴ D+ C=180 °
(两直线平行,同旁内角互补)
即 C=180 °- D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。
练习2
C
B
A
D
如图是梯形有上底的一部分。 已经量得 A= 115°,
D=100°,梯形另外两个角各是多少度?
复习回顾
新课学习
巩固练习
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
复习回顾
新课学习
巩固练习
课堂小结
练习2:
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD( )
② ∵∠1=∠B( )
∴EC∥BD( )
③ ∵∠2+∠B=180°( )
∴EC∥BD( )
④ ∵AB∥CD( )
∴ ∠3=∠C( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
∴ ∠2+∠C= 180° ( )
E
A
C
D
B
1
2
3
4
同位角相等,两直线平行
两直线平行,内错角相等
已知
已知
已知
已知
已知
已知
内错角相等,两直线平行
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
说明:①、②、③是平行线的判定的应用; ④、⑤、⑥是平行线的性质的应用.
综合应用:
A
B
C
D
E
F
1
2
3
1、填空:
(1)、∵ ∠A=____, (已知)
AC∥ED ,(_____________________)
(2)、 ∵AB ∥______, (已知)
∠2= ∠4,(______________________)
4
5
(3)、 ___ ∥___, (已知)
∠B= ∠3. (___________ ___________)
试一试,你准行!
模仿上题自己编题。(考查平行线的性质或判定)
∠4
同位角相等,两直线平行。
DF
两直线平行, 内错角相等。
AB
DF
两直线平行, 同位角相等.
判定
性质
性质
∴
∴
∴
∵
练习1:
如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
(3)从∠1=110 °可以知道∠4是多少度?为什么?
解:∠3=110°
理由如下
∵AB∥CD(已知)
∴∠1=∠3(两直线平行,同位角相等)
又∵ ∠1=110°(已知)
∴∠3=110°(等量代换)
4、练习
A
B
D
C
E
2
4
3
1
解:∠4=70°
理由如下
∵AB∥CD(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
又∵ ∠1=110°(已知)
∴∠4=70°
请同学们注意:解题中可别把平行线的判定和性质搞混了。由角的已知条件推出两线平行的结论是平行线的判定;而由两线的平行条件推出角的结论则是平行线的性质。
解:∠2=110°
理由如下:
∵AB∥CD(已知)
∴∠1=∠2(两直线平行,内错角相等)
又∵ ∠1=110°(已知)
∴∠2=110°(等量代换)
Bye!
平行线的判定方法有哪三种?它
们是先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
问题
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
问题
A
B
P
C
D
E
F
2
1
A
B
C
D
E
F
2
1
E’
F’
3
4
5
6
8
7
平行线的性质1
两条平行线被第三条直线所截,同位
角相等。
简单说成:两直线平行,同位角相等。
a//b (已知)
1= 2 (两直线平行,同位角相等)
又 1= 3(对顶角相等)
3= 2(等量代换)
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 3与 2有什么关系?
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
结论
c
2
3
1
b
a
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
如图:已知a//b,那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放
复习回顾
新课学习
巩固练习
课堂小结
c
d
a
b
3
4
2
1
例2 如图所示 ∠1 =∠2
说明 : ∠3 =∠4
说明:∵ ∠1 =∠2(已知)
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行,内错角相等)
说明:因为 AD∥BC,( )
§5.3 平行线的性质(一)
所以 ∠A+∠AEF=180°,
因为 ∠AEF=∠B,
所以 ∠A+∠B=180°.
所以 AD∥EF.
已知
( )
( )
( )
( )
两直线平行,同旁内角互补
已知
等量代换
同旁内角互补,两直线平行
例3 如图所示.
已知:AD∥BC,
∠AEF=∠B,
说明:AD∥EF.
平行线的“判定”与“性质”有什么不同
比一比
已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。
练习1
如图,已知直线a∥b,
∠3=131°,求∠ 1、∠2的度数。
解(1)∵∠1=∠3 (对顶角相等)
且∠3=131°(已知)
∴∠1 =131°
(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又 ∵ ∠1=131°
∴ ∠2=49°。
解:∵AD//BC (已知)
∴ A + B=180°
(两直线平行,同旁内角互补)
∴ B= 180 °- A =180 ° -115 °=65 °
∵AD//BC (已知)
∴ D+ C=180 °
(两直线平行,同旁内角互补)
即 C=180 °- D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。
练习2
C
B
A
D
如图是梯形有上底的一部分。 已经量得 A= 115°,
D=100°,梯形另外两个角各是多少度?
复习回顾
新课学习
巩固练习
课堂小结
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
复习回顾
新课学习
巩固练习
课堂小结
练习2:
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD( )
② ∵∠1=∠B( )
∴EC∥BD( )
③ ∵∠2+∠B=180°( )
∴EC∥BD( )
④ ∵AB∥CD( )
∴ ∠3=∠C( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
∴ ∠2+∠C= 180° ( )
E
A
C
D
B
1
2
3
4
同位角相等,两直线平行
两直线平行,内错角相等
已知
已知
已知
已知
已知
已知
内错角相等,两直线平行
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,同旁内角互补
说明:①、②、③是平行线的判定的应用; ④、⑤、⑥是平行线的性质的应用.
综合应用:
A
B
C
D
E
F
1
2
3
1、填空:
(1)、∵ ∠A=____, (已知)
AC∥ED ,(_____________________)
(2)、 ∵AB ∥______, (已知)
∠2= ∠4,(______________________)
4
5
(3)、 ___ ∥___, (已知)
∠B= ∠3. (___________ ___________)
试一试,你准行!
模仿上题自己编题。(考查平行线的性质或判定)
∠4
同位角相等,两直线平行。
DF
两直线平行, 内错角相等。
AB
DF
两直线平行, 同位角相等.
判定
性质
性质
∴
∴
∴
∵
练习1:
如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
(3)从∠1=110 °可以知道∠4是多少度?为什么?
解:∠3=110°
理由如下
∵AB∥CD(已知)
∴∠1=∠3(两直线平行,同位角相等)
又∵ ∠1=110°(已知)
∴∠3=110°(等量代换)
4、练习
A
B
D
C
E
2
4
3
1
解:∠4=70°
理由如下
∵AB∥CD(已知)
∴∠1+∠4=180°(两直线平行,同旁内角互补)
又∵ ∠1=110°(已知)
∴∠4=70°
请同学们注意:解题中可别把平行线的判定和性质搞混了。由角的已知条件推出两线平行的结论是平行线的判定;而由两线的平行条件推出角的结论则是平行线的性质。
解:∠2=110°
理由如下:
∵AB∥CD(已知)
∴∠1=∠2(两直线平行,内错角相等)
又∵ ∠1=110°(已知)
∴∠2=110°(等量代换)
Bye!
