苏教版六年级数学下册第三单元第2课时例2解决问题的策略(2)课件(31页PPT)
文档属性
| 名称 | 苏教版六年级数学下册第三单元第2课时例2解决问题的策略(2)课件(31页PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 10:58:50 | ||
图片预览



文档简介
第2课时 3.2解决问题的策略
苏教版 六年级数学下册
新知导入
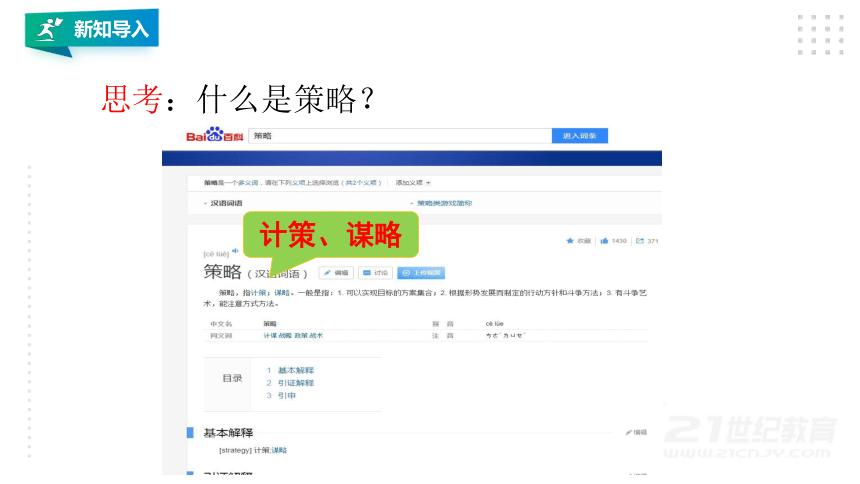
思考:什么是策略?
计策、谋略
新知导入
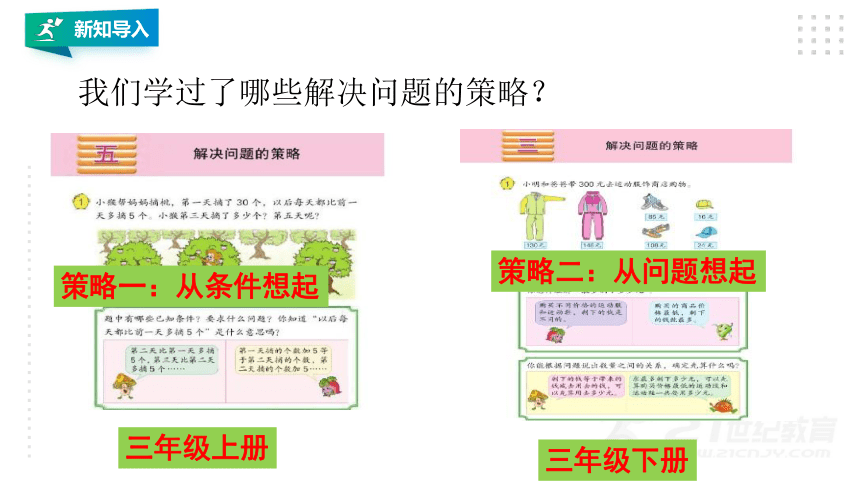
我们学过了哪些解决问题的策略?
三年级上册
三年级下册
策略一:从条件想起
策略二:从问题想起
新知导入
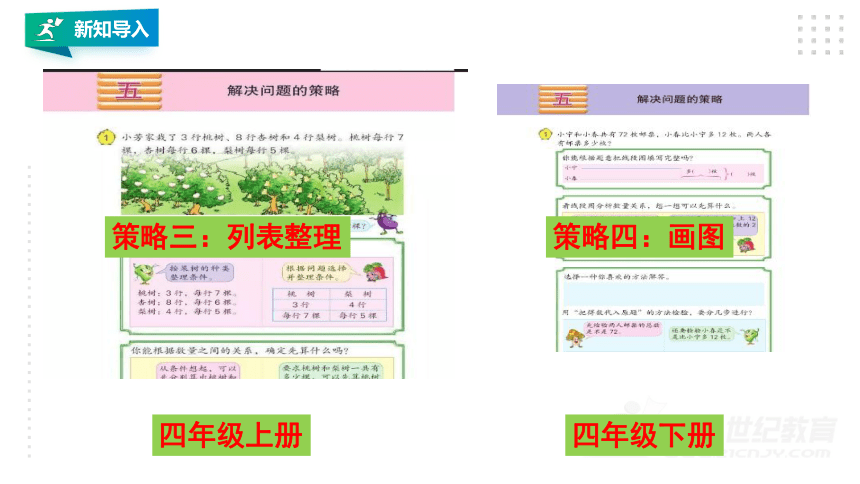
四年级上册
四年级下册
策略三:列表整理
策略四:画图
新知导入
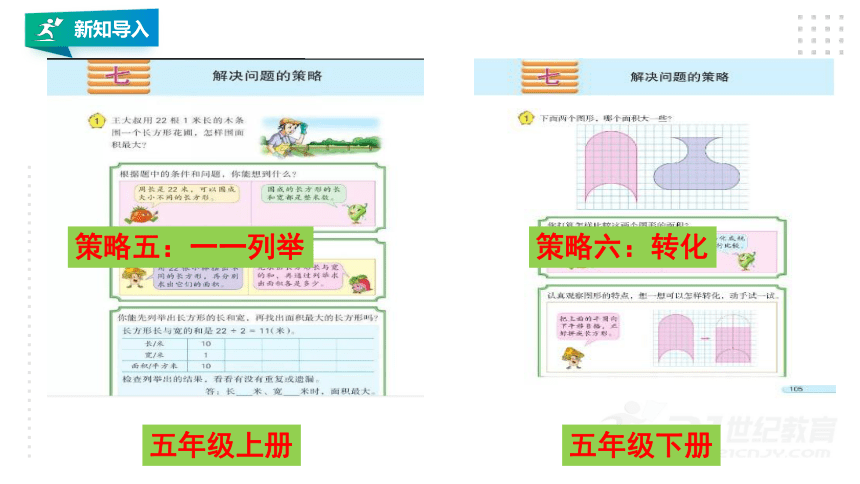
五年级上册
五年级下册
策略五:一一列举
策略六:转化
新知导入
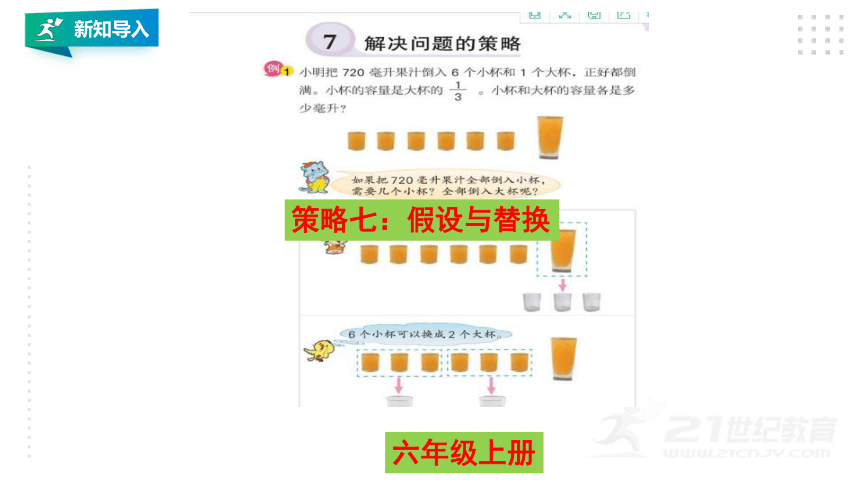
六年级上册
策略七:假设与替换
新知讲解
例2:全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
导学单:
1.从题目中我们可以获得哪些数学信息?
2.通过课本阅读,我们运用了哪些策略来解决这个问题?
3.除了课本给我们提供的解决方法以外,还有其他的策略可以找到答案吗?
1
2
3
4
检
新知讲解
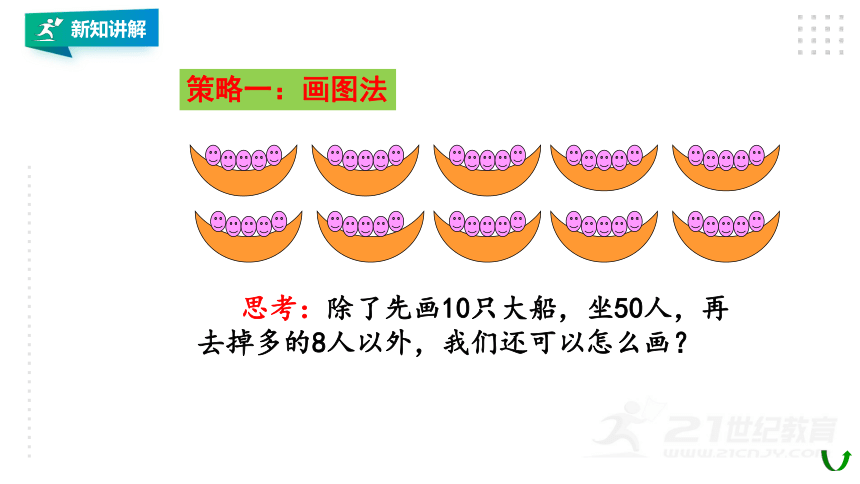
策略一:画图法
思考:除了先画10只大船,坐50人,再去掉多的8人以外,我们还可以怎么画?
新知讲解
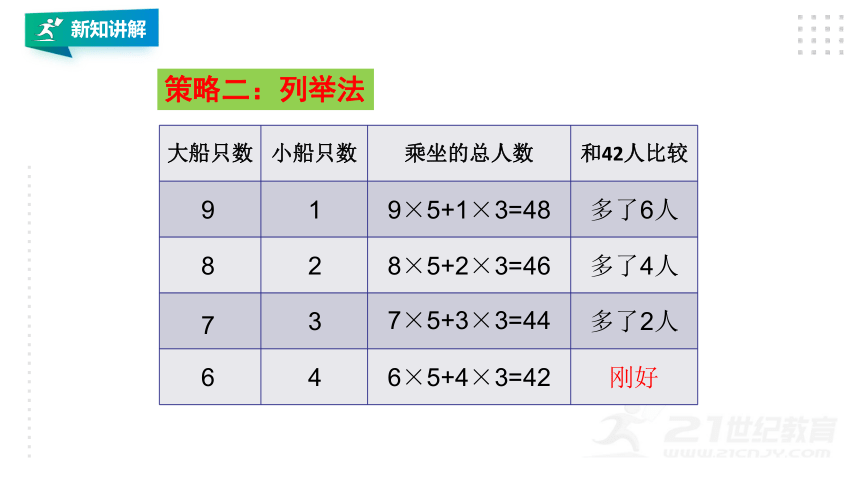
大船只数
小船只数
乘坐的总人数
和42人比较
9
8
7
6
4
3
2
1
9×5+1×3=48
8×5+2×3=46
7×5+3×3=44
6×5+4×3=42
多了6人
多了4人
多了2人
刚好
策略二:列举法
新知讲解
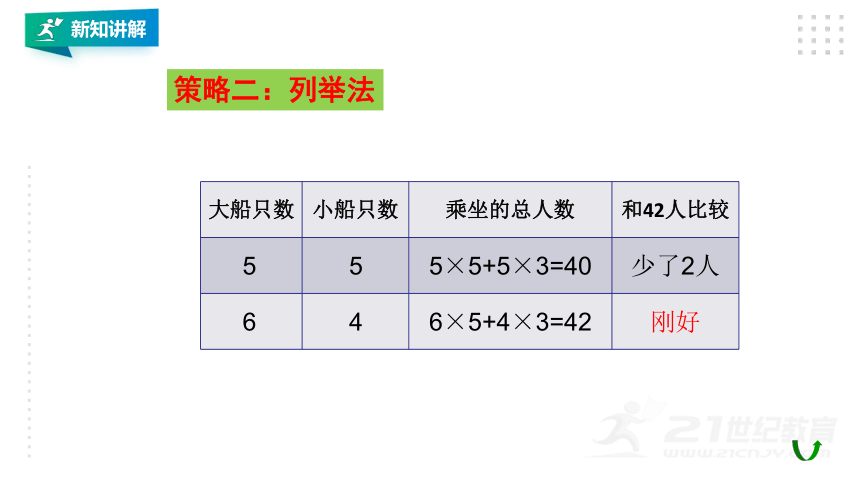
大船只数
小船只数
乘坐的总人数
和42人比较
6
4
6×5+4×3=42
刚好
5
5
5×5+5×3=40
少了2人
策略二:列举法
新知讲解
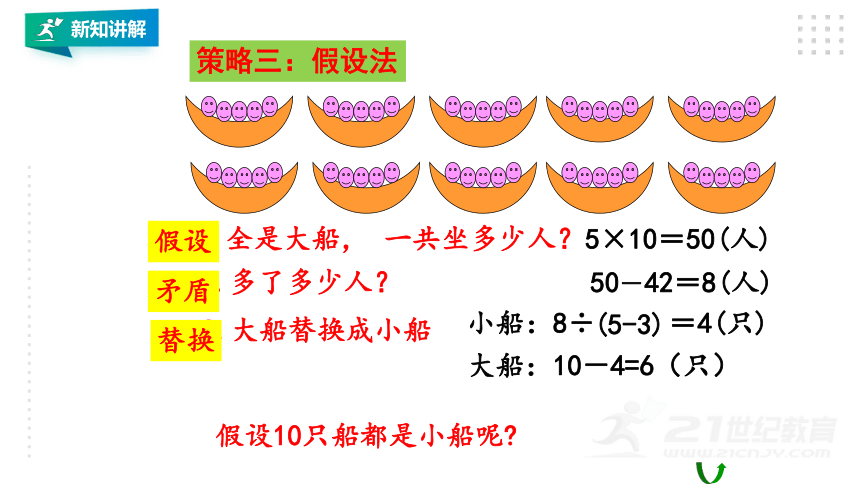
1.全是大船, 一共坐多少人?
5×10=50(人)
50-42=8(人)
3.大船替换成小船
小船:8÷ =4(只)
假设10只船都是小船呢?
大船:10-4=6(只)
2.多了多少人?
策略三:假设法
假设
矛盾
替换
(5-3)
新知讲解
大船只数+小船只数=10
大船坐的人数+小船坐的人数=42
5X+3(10-x)=42
5X+(30-3x)=42
5X-3x+30=42
2X+30=42
2X=12
X=6
小船: 10-6=4(只)
解:设大船有x只,则小船有(10-x)只。
例2:全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
策略四:方程法
新知讲解
思考:我们得出的结果是否正确呢?
1.检验总人数。
2.检验船的只数。
5×6+3×4=42(人)
答:租用的大船有6只,租用的小船有4只。
6+4=10(只)
答的时候不能答错!
课堂总结
课堂总结
通过回顾解决问题的过程,你有什么体会?
画图、列举、先假设再调整都是解决问题的有效策略。
分析和解决同一个问题,可以用不同的策略。
要学会根据具体问题灵活选择策略。
课堂练习
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
(1)按照下面的步骤画图。
① 画8个圆,表示一共有8只动物。
② 假设8只都是鸡,给每只动物画2条腿。算一算画出的腿比22条少多少条。
③ 一只兔比一只鸡多2条腿,给其中的几只动物添上2条腿,使画出的腿正好是22条。
④ 鸡有( )只,兔有( )只。
5
3
练一练
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
(2)先假设鸡和兔同样多,再调整。
多2条
5
5×2+3×4 =22
3
刚好
练一练
1.全是兔子, 一共有多少腿?
4×8=32(条)
3.兔子替换成鸡
鸡 :10÷ =5(只)
假设8只全是鸡呢?
兔子:8-5=3(只)
2.多了几条腿?
假设
矛盾
替换
(4-2)
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
练一练
32-22=10(人)
只看到这些动物的腿,一共22条。
1.命令鸡和兔各抬起1条腿。
共少了8条
2.再命令鸡和兔各抬起1条腿。
又少了8条
3.剩下几条腿是谁的?
4.说明兔有多少只?鸡呢?
趣味解法
你知道吗?
鸡兔同笼
“鸡兔同笼”问题出自我国古代数学名著《孙子算经》,书中的题目是这样的人:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
课后探究:关于这道题的解法,还有很多有趣的方法,课后同学们,可以通过自己探究或者查询资料的方法去见识更多、更好玩的方法!
1元的枚数
5角的枚数
总元数
和10元比较
1
(1)1元和5角的硬币一共13枚,共有10元。1元和5角的硬币各有多少枚?
12
1+12×0.5=7
少了3元
3
10
3+10×0.5=8
少了2元
5
8
5+8×0.5=9
少了1元
7
6
7+6×0.5=10
刚好
根据表中数据,想一想、填一填,并找出答案。
基础练习
(2)六年级同学制作了78件蝴蝶标本,贴在9块展板上展出。大展板和小展板各有多少块?
1块小展板上有6件蝴蝶标本,
1块大展板上有10件蝴蝶标本。
基础练习
策略一:列表法。假设两种展板的块数,计算标本总件数,再进行调整。
大展板块数
小展板块数
蝴蝶标本总件数
和78件比较
5
4
10×5+6×4=74
少了4件
10×6+6×3=78
刚好
3
6
9×10=90(件)90-78=12 (件)
10-6=4 (件) 12÷4=3 (块)
9-3=6 (块)
答:有6块大展板,有3块小展板
策略二:假设法。假设9块都是大展板。
(3)某次数学竞赛共20道题,每做对一题得5分,每做错一题倒扣1分。小华参加了这次比赛,共得了64分。小华做对了几题?
拓展练习
假设20题全做对。
一共得分:
20×5=100(分)
由于每把一道错题看成一道对题就多得分
5+1=6(分)
比实际多得:
100- 64=36(分)
做错的题有:
36÷6=6(题)
做对的题有:
20- 6=14(题)
课堂总结
通过本节课的学习,你有哪些收获?
板书设计
解决问题的策略
策略一:画图法
策略二:列表法
策略三:假设法
策略四:方程法
作业布置
作业:练习五第6、7、8题
https://www.21cnjy.com/help/help_extract.php
苏教版 六年级数学下册
新知导入
思考:什么是策略?
计策、谋略
新知导入
我们学过了哪些解决问题的策略?
三年级上册
三年级下册
策略一:从条件想起
策略二:从问题想起
新知导入
四年级上册
四年级下册
策略三:列表整理
策略四:画图
新知导入
五年级上册
五年级下册
策略五:一一列举
策略六:转化
新知导入
六年级上册
策略七:假设与替换
新知讲解
例2:全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
导学单:
1.从题目中我们可以获得哪些数学信息?
2.通过课本阅读,我们运用了哪些策略来解决这个问题?
3.除了课本给我们提供的解决方法以外,还有其他的策略可以找到答案吗?
1
2
3
4
检
新知讲解
策略一:画图法
思考:除了先画10只大船,坐50人,再去掉多的8人以外,我们还可以怎么画?
新知讲解
大船只数
小船只数
乘坐的总人数
和42人比较
9
8
7
6
4
3
2
1
9×5+1×3=48
8×5+2×3=46
7×5+3×3=44
6×5+4×3=42
多了6人
多了4人
多了2人
刚好
策略二:列举法
新知讲解
大船只数
小船只数
乘坐的总人数
和42人比较
6
4
6×5+4×3=42
刚好
5
5
5×5+5×3=40
少了2人
策略二:列举法
新知讲解
1.全是大船, 一共坐多少人?
5×10=50(人)
50-42=8(人)
3.大船替换成小船
小船:8÷ =4(只)
假设10只船都是小船呢?
大船:10-4=6(只)
2.多了多少人?
策略三:假设法
假设
矛盾
替换
(5-3)
新知讲解
大船只数+小船只数=10
大船坐的人数+小船坐的人数=42
5X+3(10-x)=42
5X+(30-3x)=42
5X-3x+30=42
2X+30=42
2X=12
X=6
小船: 10-6=4(只)
解:设大船有x只,则小船有(10-x)只。
例2:全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
策略四:方程法
新知讲解
思考:我们得出的结果是否正确呢?
1.检验总人数。
2.检验船的只数。
5×6+3×4=42(人)
答:租用的大船有6只,租用的小船有4只。
6+4=10(只)
答的时候不能答错!
课堂总结
课堂总结
通过回顾解决问题的过程,你有什么体会?
画图、列举、先假设再调整都是解决问题的有效策略。
分析和解决同一个问题,可以用不同的策略。
要学会根据具体问题灵活选择策略。
课堂练习
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
(1)按照下面的步骤画图。
① 画8个圆,表示一共有8只动物。
② 假设8只都是鸡,给每只动物画2条腿。算一算画出的腿比22条少多少条。
③ 一只兔比一只鸡多2条腿,给其中的几只动物添上2条腿,使画出的腿正好是22条。
④ 鸡有( )只,兔有( )只。
5
3
练一练
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
(2)先假设鸡和兔同样多,再调整。
多2条
5
5×2+3×4 =22
3
刚好
练一练
1.全是兔子, 一共有多少腿?
4×8=32(条)
3.兔子替换成鸡
鸡 :10÷ =5(只)
假设8只全是鸡呢?
兔子:8-5=3(只)
2.多了几条腿?
假设
矛盾
替换
(4-2)
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
练一练
32-22=10(人)
只看到这些动物的腿,一共22条。
1.命令鸡和兔各抬起1条腿。
共少了8条
2.再命令鸡和兔各抬起1条腿。
又少了8条
3.剩下几条腿是谁的?
4.说明兔有多少只?鸡呢?
趣味解法
你知道吗?
鸡兔同笼
“鸡兔同笼”问题出自我国古代数学名著《孙子算经》,书中的题目是这样的人:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
课后探究:关于这道题的解法,还有很多有趣的方法,课后同学们,可以通过自己探究或者查询资料的方法去见识更多、更好玩的方法!
1元的枚数
5角的枚数
总元数
和10元比较
1
(1)1元和5角的硬币一共13枚,共有10元。1元和5角的硬币各有多少枚?
12
1+12×0.5=7
少了3元
3
10
3+10×0.5=8
少了2元
5
8
5+8×0.5=9
少了1元
7
6
7+6×0.5=10
刚好
根据表中数据,想一想、填一填,并找出答案。
基础练习
(2)六年级同学制作了78件蝴蝶标本,贴在9块展板上展出。大展板和小展板各有多少块?
1块小展板上有6件蝴蝶标本,
1块大展板上有10件蝴蝶标本。
基础练习
策略一:列表法。假设两种展板的块数,计算标本总件数,再进行调整。
大展板块数
小展板块数
蝴蝶标本总件数
和78件比较
5
4
10×5+6×4=74
少了4件
10×6+6×3=78
刚好
3
6
9×10=90(件)90-78=12 (件)
10-6=4 (件) 12÷4=3 (块)
9-3=6 (块)
答:有6块大展板,有3块小展板
策略二:假设法。假设9块都是大展板。
(3)某次数学竞赛共20道题,每做对一题得5分,每做错一题倒扣1分。小华参加了这次比赛,共得了64分。小华做对了几题?
拓展练习
假设20题全做对。
一共得分:
20×5=100(分)
由于每把一道错题看成一道对题就多得分
5+1=6(分)
比实际多得:
100- 64=36(分)
做错的题有:
36÷6=6(题)
做对的题有:
20- 6=14(题)
课堂总结
通过本节课的学习,你有哪些收获?
板书设计
解决问题的策略
策略一:画图法
策略二:列表法
策略三:假设法
策略四:方程法
作业布置
作业:练习五第6、7、8题
https://www.21cnjy.com/help/help_extract.php
