1.4.3 整式的乘法一课一练(含答案)
文档属性
| 名称 | 1.4.3 整式的乘法一课一练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 866.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 12:31:03 | ||
图片预览


文档简介
12560300121158001.4.3 整式的乘法一课一练
一、选择题。
1.若(x+a)(x+b)=x2+4x+3,则a+b的值为( )
A.3 B.﹣3 C.4 D.﹣4
2.已知a、b、c三个数中有两个奇数,一个偶数,n是整数,如果S=(a+n+1)+(b+2n+2)+(c+3n+3),那么( )
A.S是偶数
B.S是奇数
C.S的奇偶性与n的奇偶性相同
D.S的奇偶不能确定
3.已知(x﹣2)(x2+mx+n)的乘积项中不含x2和x项,则m,n的值分别为( )
A.m=2,n=4 B.m=3,n=6 C.m=﹣2,n=﹣4 D.m=﹣3,n=﹣6
4.根据图1的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么根据图2的面积可以说明多项式的乘法运算是( )
A.(a+3b)(a+b)=a2+4ab+3b2
B.(a+3b)(a+b)=a2+3b2
C.(b+3a)(b+a)=b2+4ab+3a2
D.(a+3b)(a﹣b)=a2+2ab﹣3b2
5.现有如图所示的卡片若干张,其中A类、B类为正方形卡片,C类为长方形卡片,若用此三类卡片拼成一个长为a+2b,宽为a+b的大长方形,则需要C类卡片张数为( )
A.1 B.2 C.3 D.4
二、填空题。
6.计算:(3﹣π)0= ;(﹣2x2y)3= ;(x+3)(x﹣5)= .
7.若x+y=3且xy=1,则代数式(1+x)(1+y)= .
8.下列有四个结论.其中正确的是 .
①若(x﹣1)x+1=1,则x只能是2;
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,则a=1;
③若a+b=10,ab=2,则a﹣b=2;
④若4x=a,8y=b,则23y﹣2x可表示.
9.在数学综合与实践课上,老师给出了一组等式:1×2×3×4+1=(12+3×1+1)2,2×3×4×5+1=(22+3×2+1)2,3×4×5×6+1=(32+3×3+1)2,…根据你的观察,则:n×(n+1)×(n+2)×(n+3)+1= .
三、解答题。
10.化简:
(1)(2x)3(﹣5xy2); (2)(3x+2)(x+2).
11.如果关于x的多项式2x+a与x2﹣bx﹣2的乘积展开式中没有二次项,且常数项为10,求a+2b的值.
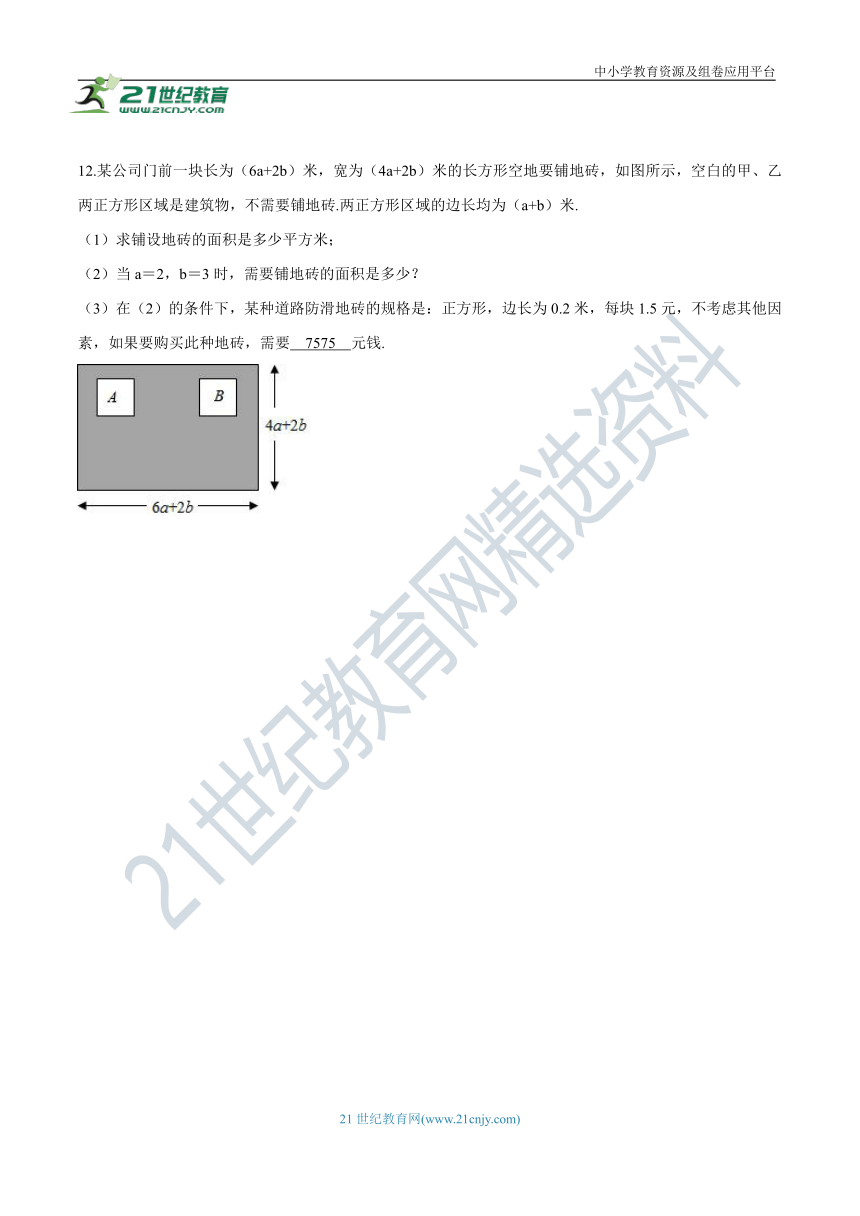
12.某公司门前一块长为(6a+2b)米,宽为(4a+2b)米的长方形空地要铺地砖,如图所示,空白的甲、乙两正方形区域是建筑物,不需要铺地砖.两正方形区域的边长均为(a+b)米.
(1)求铺设地砖的面积是多少平方米;
(2)当a=2,b=3时,需要铺地砖的面积是多少?
(3)在(2)的条件下,某种道路防滑地砖的规格是:正方形,边长为0.2米,每块1.5元,不考虑其他因素,如果要购买此种地砖,需要 7575 元钱.
答案
一、选择题。
1.C. 2.A .3 .A. 4.A. 5.C.
二、填空题。
6.:1,﹣8x6y3;x2﹣2x﹣15.
7.:5.
8.:②④.
9.:(n2+3n+1)2.
三、解答题。
10.解:(1)原式=8x3?(﹣5xy2)
=﹣8x3?5xy2
=﹣40x4y2;
(2)原式=3x2+6x+2x+4
=3x2+8x+4.
11.解:(2x+a)(x2﹣bx﹣2)
=2x3﹣2bx2﹣4x+ax2﹣abx﹣2a
=2x3+(a﹣2b)x2+(﹣4﹣ab)x﹣2a,
∵乘积展开式中没有二次项,且常数项为10,
∴a﹣2b=0且﹣2a=10,
解得a=﹣5,b=﹣2.5,
∴a+2b=﹣5+2×(﹣2.5)=﹣10.
12.解:(1)铺设地砖的面积为:(6a+2b)(4a+2b)﹣2(a+b)2
=24a2+20ab+4b2﹣2a2﹣4ab﹣2b2
=22a2+16ab+2b2(平方米),
答:铺设地砖的面积为22a2+16ab+2b2平方米;
(2)当a=2,b=3时,
原式=22×22+16×2×3+2×32
=202(平方米),
答:当a=2,b=3时,需要铺地砖的面积是202平方米;
(3)202÷0.22×1.5=7575(元),
故答案为:7575.
一、选择题。
1.若(x+a)(x+b)=x2+4x+3,则a+b的值为( )
A.3 B.﹣3 C.4 D.﹣4
2.已知a、b、c三个数中有两个奇数,一个偶数,n是整数,如果S=(a+n+1)+(b+2n+2)+(c+3n+3),那么( )
A.S是偶数
B.S是奇数
C.S的奇偶性与n的奇偶性相同
D.S的奇偶不能确定
3.已知(x﹣2)(x2+mx+n)的乘积项中不含x2和x项,则m,n的值分别为( )
A.m=2,n=4 B.m=3,n=6 C.m=﹣2,n=﹣4 D.m=﹣3,n=﹣6
4.根据图1的面积可以说明多项式的乘法运算(2a+b)(a+b)=2a2+3ab+b2,那么根据图2的面积可以说明多项式的乘法运算是( )
A.(a+3b)(a+b)=a2+4ab+3b2
B.(a+3b)(a+b)=a2+3b2
C.(b+3a)(b+a)=b2+4ab+3a2
D.(a+3b)(a﹣b)=a2+2ab﹣3b2
5.现有如图所示的卡片若干张,其中A类、B类为正方形卡片,C类为长方形卡片,若用此三类卡片拼成一个长为a+2b,宽为a+b的大长方形,则需要C类卡片张数为( )
A.1 B.2 C.3 D.4
二、填空题。
6.计算:(3﹣π)0= ;(﹣2x2y)3= ;(x+3)(x﹣5)= .
7.若x+y=3且xy=1,则代数式(1+x)(1+y)= .
8.下列有四个结论.其中正确的是 .
①若(x﹣1)x+1=1,则x只能是2;
②若(x﹣1)(x2+ax+1)的运算结果中不含x2项,则a=1;
③若a+b=10,ab=2,则a﹣b=2;
④若4x=a,8y=b,则23y﹣2x可表示.
9.在数学综合与实践课上,老师给出了一组等式:1×2×3×4+1=(12+3×1+1)2,2×3×4×5+1=(22+3×2+1)2,3×4×5×6+1=(32+3×3+1)2,…根据你的观察,则:n×(n+1)×(n+2)×(n+3)+1= .
三、解答题。
10.化简:
(1)(2x)3(﹣5xy2); (2)(3x+2)(x+2).
11.如果关于x的多项式2x+a与x2﹣bx﹣2的乘积展开式中没有二次项,且常数项为10,求a+2b的值.
12.某公司门前一块长为(6a+2b)米,宽为(4a+2b)米的长方形空地要铺地砖,如图所示,空白的甲、乙两正方形区域是建筑物,不需要铺地砖.两正方形区域的边长均为(a+b)米.
(1)求铺设地砖的面积是多少平方米;
(2)当a=2,b=3时,需要铺地砖的面积是多少?
(3)在(2)的条件下,某种道路防滑地砖的规格是:正方形,边长为0.2米,每块1.5元,不考虑其他因素,如果要购买此种地砖,需要 7575 元钱.
答案
一、选择题。
1.C. 2.A .3 .A. 4.A. 5.C.
二、填空题。
6.:1,﹣8x6y3;x2﹣2x﹣15.
7.:5.
8.:②④.
9.:(n2+3n+1)2.
三、解答题。
10.解:(1)原式=8x3?(﹣5xy2)
=﹣8x3?5xy2
=﹣40x4y2;
(2)原式=3x2+6x+2x+4
=3x2+8x+4.
11.解:(2x+a)(x2﹣bx﹣2)
=2x3﹣2bx2﹣4x+ax2﹣abx﹣2a
=2x3+(a﹣2b)x2+(﹣4﹣ab)x﹣2a,
∵乘积展开式中没有二次项,且常数项为10,
∴a﹣2b=0且﹣2a=10,
解得a=﹣5,b=﹣2.5,
∴a+2b=﹣5+2×(﹣2.5)=﹣10.
12.解:(1)铺设地砖的面积为:(6a+2b)(4a+2b)﹣2(a+b)2
=24a2+20ab+4b2﹣2a2﹣4ab﹣2b2
=22a2+16ab+2b2(平方米),
答:铺设地砖的面积为22a2+16ab+2b2平方米;
(2)当a=2,b=3时,
原式=22×22+16×2×3+2×32
=202(平方米),
答:当a=2,b=3时,需要铺地砖的面积是202平方米;
(3)202÷0.22×1.5=7575(元),
故答案为:7575.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
