数学:第七章锐角三角函数复习课件(苏科版九年级下)2
文档属性
| 名称 | 数学:第七章锐角三角函数复习课件(苏科版九年级下)2 |

|
|
| 格式 | zip | ||
| 文件大小 | 216.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-08 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
第七章
锐角三角函数
基础知识和能力概要
中考要求
1)基本概念:包括直角三角形的基本元素,边角关系,锐角三角函数等
2)基本计算:包括对角的计算,对边的计算,应用某种关系计算等。
3)基本应用:主要题型是:测量,航海,坡面改造,光学,修筑公路等其主要思想方法是:方程思想,数形结合,化归转化,数学建模等。
sin A=
cos A=
tan A=
cot A=
知识 概要
(一)锐角三角函数的概念
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
0<sin A<1,0<cos A<1
这些函数值之间有什么关系?
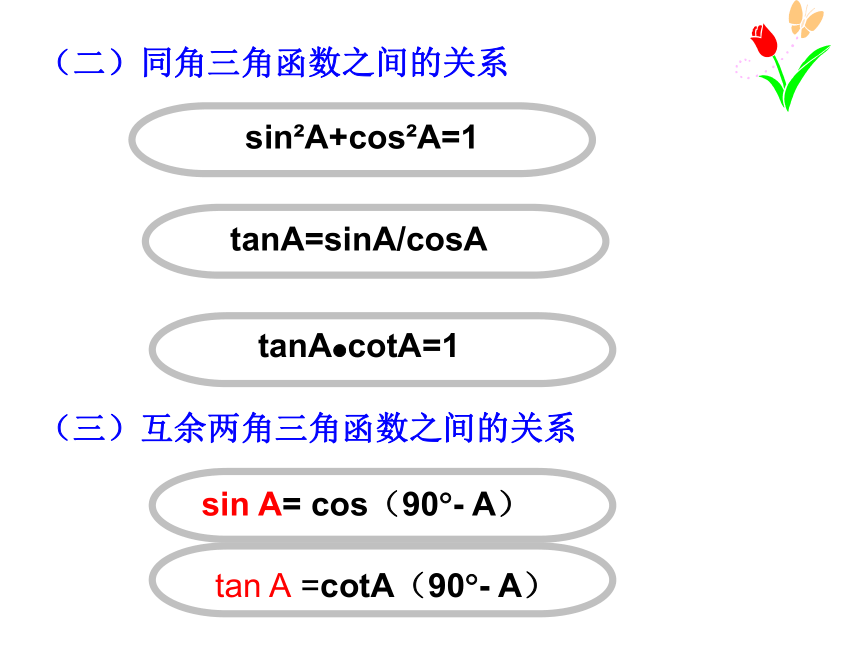
(二)同角三角函数之间的关系
sin A+cos A=1
tanA=sinA/cosA
tanA cotA=1
(三)互余两角三角函数之间的关系
sin A= cos(90 - A)
tan A =cotA(90 - A)
知识 概要
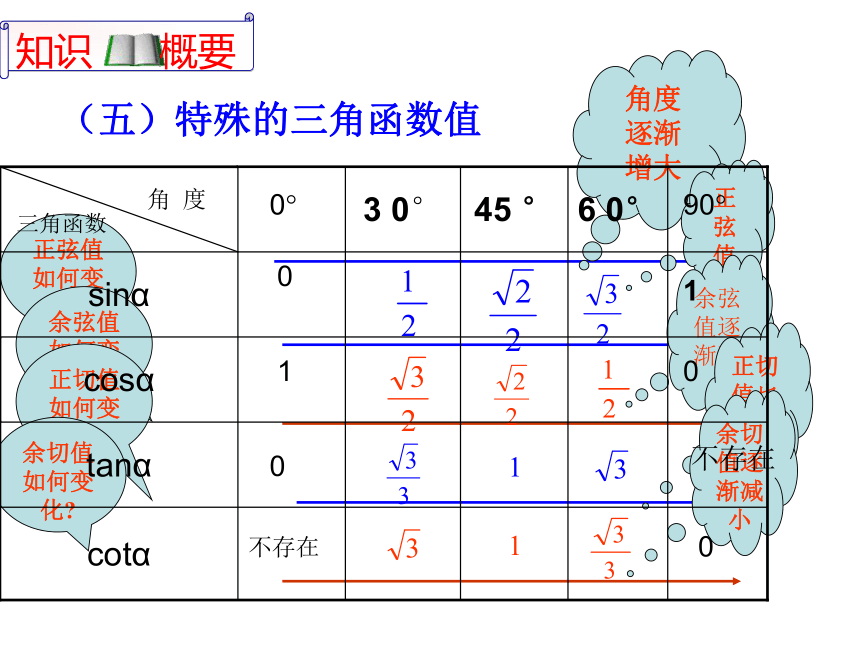
(四)三角函数值的变化规律
1)当角度在0---90之间变化时,正弦值(正切值)随着角度的增大(或减小)而增大(或减小)
2)当角度在0---90之间变化时,余弦值(余切值)随着角度的增大(或减小)而减小(或增大)
1
1
角度
逐渐
增大
正弦值如何变化
正弦值也增大
余弦值如何变化
余弦值逐渐减小
正切值如何变化
正切值也随之增大
余切值如何变化
余切值逐渐减小
cotα
tanα
cosα
sinα
6 0°
45 °
3 0°
角 度
三角函数
0
90
0
1
0
0
1
不存在
不存在
0
(五)特殊的三角函数值
知识 概要
知识 概要
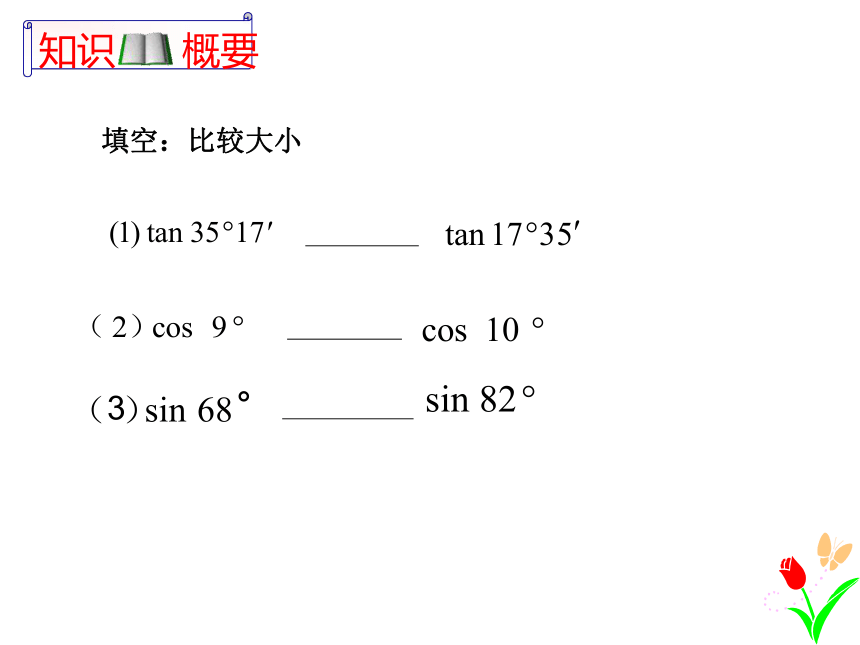
填空:比较大小
°
68
sin
3
)
(
知识 概要
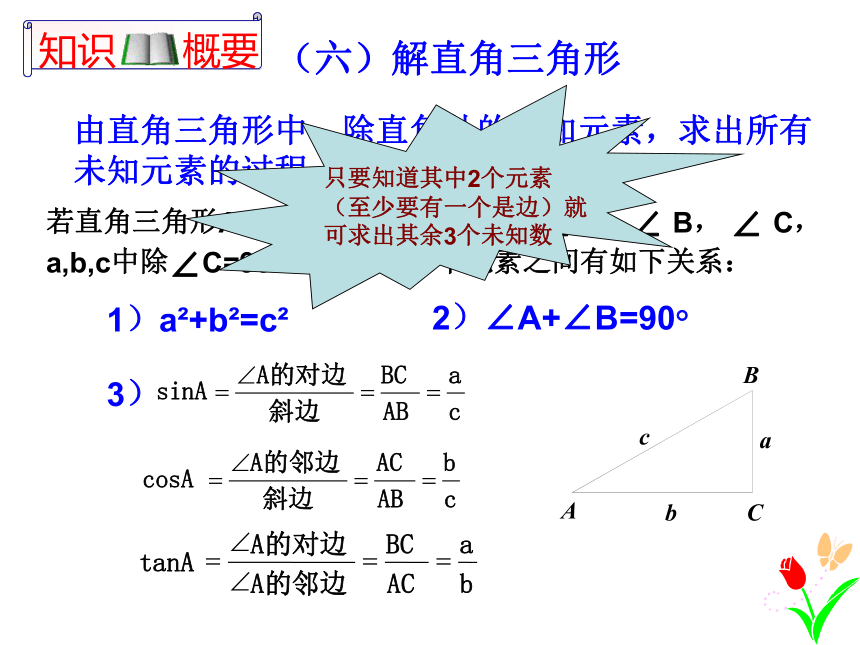
(六)解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
若直角三角形ABC中,∠C=90 ,那么∠A, ∠ B, ∠ C,a,b,c中除∠C=90°外,其余5个元素之间有如下关系:
1)a +b =c
2)∠A+∠B=90
3)
b
a
AC
BC
A的邻边
A的对边
tanA
=
=
=
只要知道其中2个元素(至少要有一个是边)就可求出其余3个未知数
1)仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
知识 概要
(七)应用问题中的几个重要概念
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方向角.如图所示:
30°
45°
B
O
A
东
西
北
南
2)方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,有i= =tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即 I = .
3)坡度(坡比),坡角的概念
☆ 考点范例解析
1.锐角三角函数的概念关系
1)在Rt ABC中,∠C=90°BC=a,AC=b若sinA ﹕ sinB = 2 ﹕3,求a ﹕b的值
锐角三角函数的概念
解法1 设AB=c由三角函数的定义得:sinA ﹕sinB=a/c ﹕b/c=a ﹕b
∴ a ﹕ b = 2/3
解法2 由三角函数的定义得:
a=csinA, b=csinB, a/b=csinA/csinB
∴ a ﹕ b=sinA/sinB = 2/3
抓住三角函数的定义是解题的关键
☆ 考点范例解析
1.锐角三角函数的概念关系
锐角三角函数的概念
2 在 ABC中∠A≠ ∠ B,∠C=90°则下列结论正确的是( )
sinA>sinB
sin A+sin B=1
sinA=sinB
若各边长都扩大为原来的2倍,则tanA也扩大为原来的2倍
A)(1)(3) B)(2)
C)(2)(4) D)(1)(2)(3)
解析:令a=3,b=4则c=5,sinA=3/5,
sinB=4/5且∠ A ≠∠ B,易知
(1)(3)都不对,故选 B)
用构造特殊的直角三角形来否定某些关系式,是解决选择题的常用方法
☆ 考点范例解析
1.锐角三角函数的概念关系
特殊角的三角函数值
2.求特殊角的三角函数值
A)锐角三角形
B)直角三角形
D)钝角三角形
C)等边三角形
C
☆ 考点范例解析
1.锐角三角函数的概念关系
特殊角的三角函数值
2.求特殊角的三角函数值
点评 融特殊角的三角函数值,简单的无理方程的计算以及数的零次幂的意义于一体是中考命题率极高的题型之一
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
互余或同角的三角函数
5.下列式中不正确的是( )
C
点评:应用互余的三角函数关系进行正弦与余弦的互化,并了解同一个锐角的三角函数关系,能运用其关系进行简单的转化运算,才能解决这类问题。
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
互余或同角的三角函数
6 在 ABC中∠C=90°化简下面的式子
7 在 ABC中∠C=90°且
求cosA的值
点评:利用互余或同角的三角函数关系的相关结论是解决这类问题的关键
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
4.解直角三角形
解直角三角形
点评:由于三角函数是边之间的比,因此利用我们熟知的按比例设为参数比的形式来求解,是处理直角三角形问题的常用方法。
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
4.解直角三角形
解直角三角形
A
B
C
8.如图小正方形的边长为1,连结小正方形的三个顶点得到 ABC,则AC边上是的高( )
点评:作BC边上的高,利用面积公式即可求出AC边的高,面积法是解决此类问题的有效途径
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
4.解直角三角形
5.解直角三角形的应用
解直角三角形的应用
9.如图某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到旗杆的距离(即CE的长)为8米,测得旗杆顶 的仰角∠ECA为30°旗杆底部的俯角∠ECB为45 °则旗杆AB的高度是( )米
C
A
B
D
E
E
点评:此题属于解直角三角形的基本应用题—测量问题,要明确仰角和俯角,然后数形结合直接从图形出发解直角三角形.
10.如图某船以每小时30海里的速度先向正东方向航行,在点A处测得某岛C在北偏东60°的方向上,航行3小时到达点B,测得该岛在北偏东30°的方向上且该岛周围16海里内有暗礁
(1)试证明:点B在暗礁区外;
(2)若继续向东航行有无触暗礁的危险?
D
解:1)由题意得,∠CAB=30°,∠ABC=120 ° ,则∠C=30 ° ,BC=AB=30×3=90 > 16∴点B在暗礁区外.
2)如图过点C作CD⊥AB交AB的延长线于D点,设BD=x,在Rt BCD中,∠CBD=60°,
∴船继续向东航行没有触礁的危险。
11)如图AM,BN是一束平行的阳光从教室窗户AB射入的平面示意图,光线与地面所成的角∠AMC=30°,在教室地面的影长MN= 米,若窗户的下檐到教室地面的距离BC=1米,则窗户的上檐到教室地面的距离AC为( )米
B
此题属于光学问题的基本应用,首先要对有关生活常识有所了解,从图形入手,数形结合,将已知信息转化为解直角三角形的数学模型去解。
12)如图,一张长方形的纸片ABCD,其长AD为a,宽AB为b(a>b) ,在BC边上选取一点M,将 ABM沿着AM翻折后,B至N的位置,若N为长方形纸片ABCD的对称中心,求a/b的值。
3
点评:此题是创新综合题,要求我们对图形及其变换有较深刻的理解,并运用图形对称性和解直角三角形知识或勾股定理建立等式求解。
13)
一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心 海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里
(1)若该轮船自A按原速度原方向继续航行,在途中会不会遇到台风?
东
北
A
B
13)
一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心 海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里
(2)若该轮船自A立即提高船速,向位于东偏北30°方向,相距60海里的D港驶去继续航行,为使船在台风到达之前到达D港,问船速至少应提高多少?(提高的船速取整数)
东
北
A
B
D
30°
第七章
锐角三角函数
基础知识和能力概要
中考要求
1)基本概念:包括直角三角形的基本元素,边角关系,锐角三角函数等
2)基本计算:包括对角的计算,对边的计算,应用某种关系计算等。
3)基本应用:主要题型是:测量,航海,坡面改造,光学,修筑公路等其主要思想方法是:方程思想,数形结合,化归转化,数学建模等。
sin A=
cos A=
tan A=
cot A=
知识 概要
(一)锐角三角函数的概念
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数.
0<sin A<1,0<cos A<1
这些函数值之间有什么关系?
(二)同角三角函数之间的关系
sin A+cos A=1
tanA=sinA/cosA
tanA cotA=1
(三)互余两角三角函数之间的关系
sin A= cos(90 - A)
tan A =cotA(90 - A)
知识 概要
(四)三角函数值的变化规律
1)当角度在0---90之间变化时,正弦值(正切值)随着角度的增大(或减小)而增大(或减小)
2)当角度在0---90之间变化时,余弦值(余切值)随着角度的增大(或减小)而减小(或增大)
1
1
角度
逐渐
增大
正弦值如何变化
正弦值也增大
余弦值如何变化
余弦值逐渐减小
正切值如何变化
正切值也随之增大
余切值如何变化
余切值逐渐减小
cotα
tanα
cosα
sinα
6 0°
45 °
3 0°
角 度
三角函数
0
90
0
1
0
0
1
不存在
不存在
0
(五)特殊的三角函数值
知识 概要
知识 概要
填空:比较大小
°
68
sin
3
)
(
知识 概要
(六)解直角三角形
由直角三角形中,除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形。
若直角三角形ABC中,∠C=90 ,那么∠A, ∠ B, ∠ C,a,b,c中除∠C=90°外,其余5个元素之间有如下关系:
1)a +b =c
2)∠A+∠B=90
3)
b
a
AC
BC
A的邻边
A的对边
tanA
=
=
=
只要知道其中2个元素(至少要有一个是边)就可求出其余3个未知数
1)仰角和俯角
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
知识 概要
(七)应用问题中的几个重要概念
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于900的角,叫做方向角.如图所示:
30°
45°
B
O
A
东
西
北
南
2)方向角
45°
45°
西南
O
东北
东
西
北
南
西北
东南
坡度通常写成1∶m的形式,如i=1∶6.
坡面与水平面的夹角叫做坡角,记作a,有i= =tan a
显然,坡度越大,坡角a就越大,坡面就越陡.
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.
如图:坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面坡度(或坡比).记作i,即 I = .
3)坡度(坡比),坡角的概念
☆ 考点范例解析
1.锐角三角函数的概念关系
1)在Rt ABC中,∠C=90°BC=a,AC=b若sinA ﹕ sinB = 2 ﹕3,求a ﹕b的值
锐角三角函数的概念
解法1 设AB=c由三角函数的定义得:sinA ﹕sinB=a/c ﹕b/c=a ﹕b
∴ a ﹕ b = 2/3
解法2 由三角函数的定义得:
a=csinA, b=csinB, a/b=csinA/csinB
∴ a ﹕ b=sinA/sinB = 2/3
抓住三角函数的定义是解题的关键
☆ 考点范例解析
1.锐角三角函数的概念关系
锐角三角函数的概念
2 在 ABC中∠A≠ ∠ B,∠C=90°则下列结论正确的是( )
sinA>sinB
sin A+sin B=1
sinA=sinB
若各边长都扩大为原来的2倍,则tanA也扩大为原来的2倍
A)(1)(3) B)(2)
C)(2)(4) D)(1)(2)(3)
解析:令a=3,b=4则c=5,sinA=3/5,
sinB=4/5且∠ A ≠∠ B,易知
(1)(3)都不对,故选 B)
用构造特殊的直角三角形来否定某些关系式,是解决选择题的常用方法
☆ 考点范例解析
1.锐角三角函数的概念关系
特殊角的三角函数值
2.求特殊角的三角函数值
A)锐角三角形
B)直角三角形
D)钝角三角形
C)等边三角形
C
☆ 考点范例解析
1.锐角三角函数的概念关系
特殊角的三角函数值
2.求特殊角的三角函数值
点评 融特殊角的三角函数值,简单的无理方程的计算以及数的零次幂的意义于一体是中考命题率极高的题型之一
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
互余或同角的三角函数
5.下列式中不正确的是( )
C
点评:应用互余的三角函数关系进行正弦与余弦的互化,并了解同一个锐角的三角函数关系,能运用其关系进行简单的转化运算,才能解决这类问题。
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
互余或同角的三角函数
6 在 ABC中∠C=90°化简下面的式子
7 在 ABC中∠C=90°且
求cosA的值
点评:利用互余或同角的三角函数关系的相关结论是解决这类问题的关键
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
4.解直角三角形
解直角三角形
点评:由于三角函数是边之间的比,因此利用我们熟知的按比例设为参数比的形式来求解,是处理直角三角形问题的常用方法。
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
4.解直角三角形
解直角三角形
A
B
C
8.如图小正方形的边长为1,连结小正方形的三个顶点得到 ABC,则AC边上是的高( )
点评:作BC边上的高,利用面积公式即可求出AC边的高,面积法是解决此类问题的有效途径
☆ 考点范例解析
1.锐角三角函数的概念关系
2.求特殊角的三角函数值
3.互余或同角的三角函数关系
4.解直角三角形
5.解直角三角形的应用
解直角三角形的应用
9.如图某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到旗杆的距离(即CE的长)为8米,测得旗杆顶 的仰角∠ECA为30°旗杆底部的俯角∠ECB为45 °则旗杆AB的高度是( )米
C
A
B
D
E
E
点评:此题属于解直角三角形的基本应用题—测量问题,要明确仰角和俯角,然后数形结合直接从图形出发解直角三角形.
10.如图某船以每小时30海里的速度先向正东方向航行,在点A处测得某岛C在北偏东60°的方向上,航行3小时到达点B,测得该岛在北偏东30°的方向上且该岛周围16海里内有暗礁
(1)试证明:点B在暗礁区外;
(2)若继续向东航行有无触暗礁的危险?
D
解:1)由题意得,∠CAB=30°,∠ABC=120 ° ,则∠C=30 ° ,BC=AB=30×3=90 > 16∴点B在暗礁区外.
2)如图过点C作CD⊥AB交AB的延长线于D点,设BD=x,在Rt BCD中,∠CBD=60°,
∴船继续向东航行没有触礁的危险。
11)如图AM,BN是一束平行的阳光从教室窗户AB射入的平面示意图,光线与地面所成的角∠AMC=30°,在教室地面的影长MN= 米,若窗户的下檐到教室地面的距离BC=1米,则窗户的上檐到教室地面的距离AC为( )米
B
此题属于光学问题的基本应用,首先要对有关生活常识有所了解,从图形入手,数形结合,将已知信息转化为解直角三角形的数学模型去解。
12)如图,一张长方形的纸片ABCD,其长AD为a,宽AB为b(a>b) ,在BC边上选取一点M,将 ABM沿着AM翻折后,B至N的位置,若N为长方形纸片ABCD的对称中心,求a/b的值。
3
点评:此题是创新综合题,要求我们对图形及其变换有较深刻的理解,并运用图形对称性和解直角三角形知识或勾股定理建立等式求解。
13)
一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心 海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里
(1)若该轮船自A按原速度原方向继续航行,在途中会不会遇到台风?
东
北
A
B
13)
一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心 海里的圆形区域(包括边界)都属于台风区,当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里
(2)若该轮船自A立即提高船速,向位于东偏北30°方向,相距60海里的D港驶去继续航行,为使船在台风到达之前到达D港,问船速至少应提高多少?(提高的船速取整数)
东
北
A
B
D
30°
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
