人教版七年级数学下册5.1.1 相交线 课件(26张ppt)
文档属性
| 名称 | 人教版七年级数学下册5.1.1 相交线 课件(26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 00:00:00 | ||
图片预览







文档简介
第五章 相交线与平行线
5.1 相交线
5.1.1 相交线
学习
目标
1.理解对顶角和邻补角的概念,能在图形中辨认.
2.掌握对顶角相等的性质和它的推证过程.
3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.
1.邻补角
如果两个角具有一条________,它们的另一边互为____________,那么这两个角互为邻补角.其中一个角都叫作另一个角的_________.
2.对顶角
(1)如果两个角具有公共________并且两边互为______________,那么这两个角互为对顶角,其中一个角叫作另一个角的__________.
(2)对顶角相等.
公共边
反向延长线
邻补角
顶点
反向延长线
对顶角
1.邻补角与补角有什么相同点?有什么不同点?两者之间有什么关系?
【答案】相同点为两角之和都等于180°;不同点为邻补角一定有一条公共边,补角不一定有公共边;它们之间的关系为邻补角是特殊的补角,补角包括邻补角.
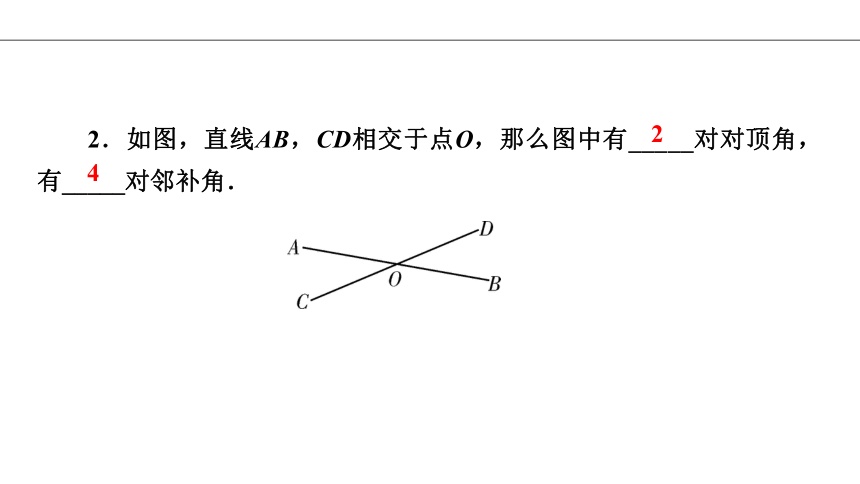
2.如图,直线AB,CD相交于点O,那么图中有_____对对顶角,有_____对邻补角.
2
4
知识点1 邻补角
【例1】 如图,直线AB,CD相交于点O,过O点画射线OE,OF,已知∠AOE=35°,∠COE=∠DOF.
(1)请你说明点E,O,F在同一条直线上;
(2)求∠AOF的度数.
?
解:(1)∵∠COE=∠DOF(已知),
∴∠DOF+∠DOE=∠COE+∠DOE,即∠EOF=∠COD=180°(等式的性质).
∴点E,O,F三点在同一条直线上(平角的定义).
(2)∵点O是直线EF上的点,
∴∠AOE与∠AOF是邻补角.
∴∠AOF=180°-∠AOE=180°-35°=145°.
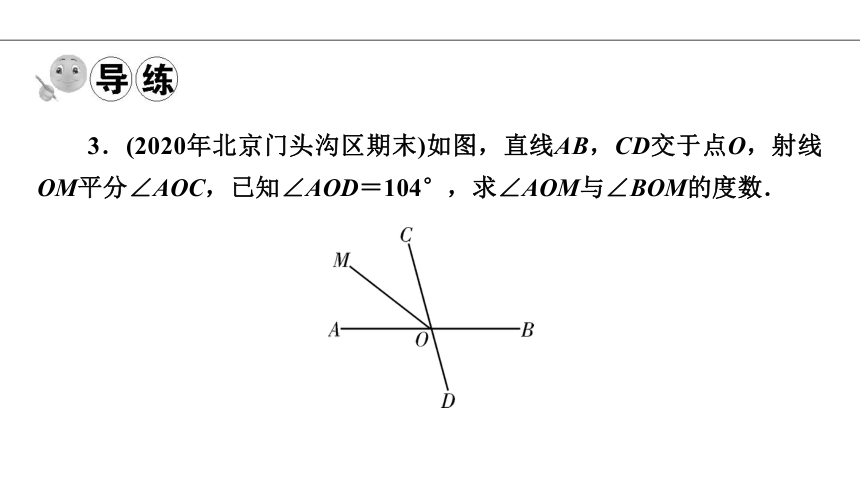
3.(2020年北京门头沟区期末)如图,直线AB,CD交于点O,射线OM平分∠AOC,已知∠AOD=104°,求∠AOM与∠BOM的度数.
易错警示:求∠AOF的度数时,易错之处是不经过说明而默认点E,O,F三点在同一条直线上,在这个前提下利用邻补角的定义求解,其原因是受图形的干扰且审题不认真,实际上,由于题目中没有指明,所以必须先根据有关的定义、定理、已知条件等说明OE与OF在同一条直线上.
知识点2 对顶角
【例2】 (2020年苏州期末)如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
(3)设∠AOC=∠BOD=α,则∠DOF=α+15°,
∴∠EOF=∠DOF=α+15°.
∴∠EOB=∠EOF+∠BOF=α+30°.
∴∠COB=2∠EOB=2α+60°,
而∠COB+∠BOD=180°,即3α+60°=180°,
解得α=40°.∴∠AOC=40°.
4.(2020年临汾期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)∠BOD的补角是__________________;
(2)若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
【第一关】 建议用时3分钟
1.(2019年东方期末)如图,直线a,b相交形成四个角,互为对顶角的是 ( )
A.∠1与∠2
B.∠2与∠3
C.∠3与∠4
D.∠2与∠4
D
2.(2020年如皋期末)如图,直线AB,CD相交于点O,已知∠AOC=40°,则∠BOD的度数为 ( )
?
?
?
A.20° B.40°
C.50° D.140°
B
3.如图,直线AB,CD相交于点O,则图中与∠BOC互为邻补角的角有_____个,分别是______________________.
2
∠AOC与∠BOD
【第二关】 建议用时6分钟
4.(2020年盐城期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
?
?
?
(1)请你数一数,图中有_____个角;
(2)若∠EOC=80°,求∠BOD的度数.
8
5.如图,直线AB,CD,EF相交于点O.
(1)∠AOD的对顶角是_________,∠EOC的对顶角是_________;
(2)∠AOC的邻补角是______________________,∠EOB的邻补角是______________________;
(3)已知∠AOC=50°,求∠BOD,∠COB的度数.
∠BOC
∠DOF
∠EOA和∠BOF
∠AOD和∠BOC
解:(3)∵∠AOC=50°,
∴∠BOD=∠AOC=50°(对顶角相等).
∵∠BOC+∠AOC=180°,
∴∠BOC=180°-∠AOC=180°-50°=130°.
【第三关】 自主选做
6.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,若∠AOC=82°,求∠BOF的度数.
5.1 相交线
5.1.1 相交线
学习
目标
1.理解对顶角和邻补角的概念,能在图形中辨认.
2.掌握对顶角相等的性质和它的推证过程.
3.通过在图形中辨认对顶角和邻补角,培养学生的识图能力.
1.邻补角
如果两个角具有一条________,它们的另一边互为____________,那么这两个角互为邻补角.其中一个角都叫作另一个角的_________.
2.对顶角
(1)如果两个角具有公共________并且两边互为______________,那么这两个角互为对顶角,其中一个角叫作另一个角的__________.
(2)对顶角相等.
公共边
反向延长线
邻补角
顶点
反向延长线
对顶角
1.邻补角与补角有什么相同点?有什么不同点?两者之间有什么关系?
【答案】相同点为两角之和都等于180°;不同点为邻补角一定有一条公共边,补角不一定有公共边;它们之间的关系为邻补角是特殊的补角,补角包括邻补角.
2.如图,直线AB,CD相交于点O,那么图中有_____对对顶角,有_____对邻补角.
2
4
知识点1 邻补角
【例1】 如图,直线AB,CD相交于点O,过O点画射线OE,OF,已知∠AOE=35°,∠COE=∠DOF.
(1)请你说明点E,O,F在同一条直线上;
(2)求∠AOF的度数.
?
解:(1)∵∠COE=∠DOF(已知),
∴∠DOF+∠DOE=∠COE+∠DOE,即∠EOF=∠COD=180°(等式的性质).
∴点E,O,F三点在同一条直线上(平角的定义).
(2)∵点O是直线EF上的点,
∴∠AOE与∠AOF是邻补角.
∴∠AOF=180°-∠AOE=180°-35°=145°.
3.(2020年北京门头沟区期末)如图,直线AB,CD交于点O,射线OM平分∠AOC,已知∠AOD=104°,求∠AOM与∠BOM的度数.
易错警示:求∠AOF的度数时,易错之处是不经过说明而默认点E,O,F三点在同一条直线上,在这个前提下利用邻补角的定义求解,其原因是受图形的干扰且审题不认真,实际上,由于题目中没有指明,所以必须先根据有关的定义、定理、已知条件等说明OE与OF在同一条直线上.
知识点2 对顶角
【例2】 (2020年苏州期末)如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的角平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
(3)设∠AOC=∠BOD=α,则∠DOF=α+15°,
∴∠EOF=∠DOF=α+15°.
∴∠EOB=∠EOF+∠BOF=α+30°.
∴∠COB=2∠EOB=2α+60°,
而∠COB+∠BOD=180°,即3α+60°=180°,
解得α=40°.∴∠AOC=40°.
4.(2020年临汾期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)∠BOD的补角是__________________;
(2)若∠EOC∶∠EOD=2∶3,求∠BOD的度数.
【第一关】 建议用时3分钟
1.(2019年东方期末)如图,直线a,b相交形成四个角,互为对顶角的是 ( )
A.∠1与∠2
B.∠2与∠3
C.∠3与∠4
D.∠2与∠4
D
2.(2020年如皋期末)如图,直线AB,CD相交于点O,已知∠AOC=40°,则∠BOD的度数为 ( )
?
?
?
A.20° B.40°
C.50° D.140°
B
3.如图,直线AB,CD相交于点O,则图中与∠BOC互为邻补角的角有_____个,分别是______________________.
2
∠AOC与∠BOD
【第二关】 建议用时6分钟
4.(2020年盐城期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
?
?
?
(1)请你数一数,图中有_____个角;
(2)若∠EOC=80°,求∠BOD的度数.
8
5.如图,直线AB,CD,EF相交于点O.
(1)∠AOD的对顶角是_________,∠EOC的对顶角是_________;
(2)∠AOC的邻补角是______________________,∠EOB的邻补角是______________________;
(3)已知∠AOC=50°,求∠BOD,∠COB的度数.
∠BOC
∠DOF
∠EOA和∠BOF
∠AOD和∠BOC
解:(3)∵∠AOC=50°,
∴∠BOD=∠AOC=50°(对顶角相等).
∵∠BOC+∠AOC=180°,
∴∠BOC=180°-∠AOC=180°-50°=130°.
【第三关】 自主选做
6.如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,若∠AOC=82°,求∠BOF的度数.
