17.1 勾股定理(第1课时) 课件(共28张PPT)
文档属性
| 名称 | 17.1 勾股定理(第1课时) 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 00:00:00 | ||
图片预览



文档简介
(共28张PPT)
人教版
八年级下
17.1
勾股定理
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.注意观察,你能有什么发现?
毕达哥拉斯(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
新知导入
A
B
C
新知导入
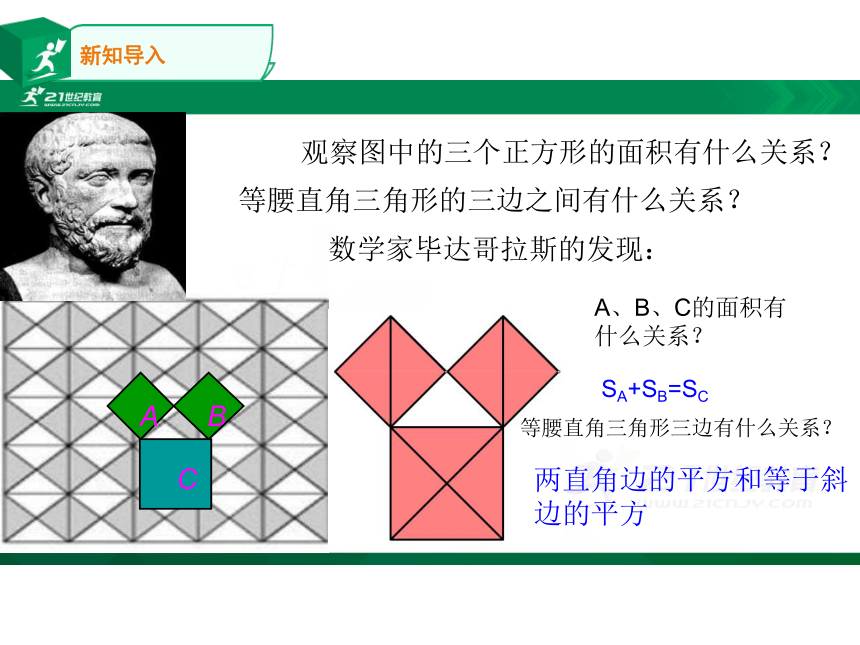
两直角边的平方和等于斜边的平方
观察图中的三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
SA+SB=SC
等腰直角三角形三边有什么关系?
进一步思考
是不是所有的直角三角形都是这样的关系呢?
新知探究
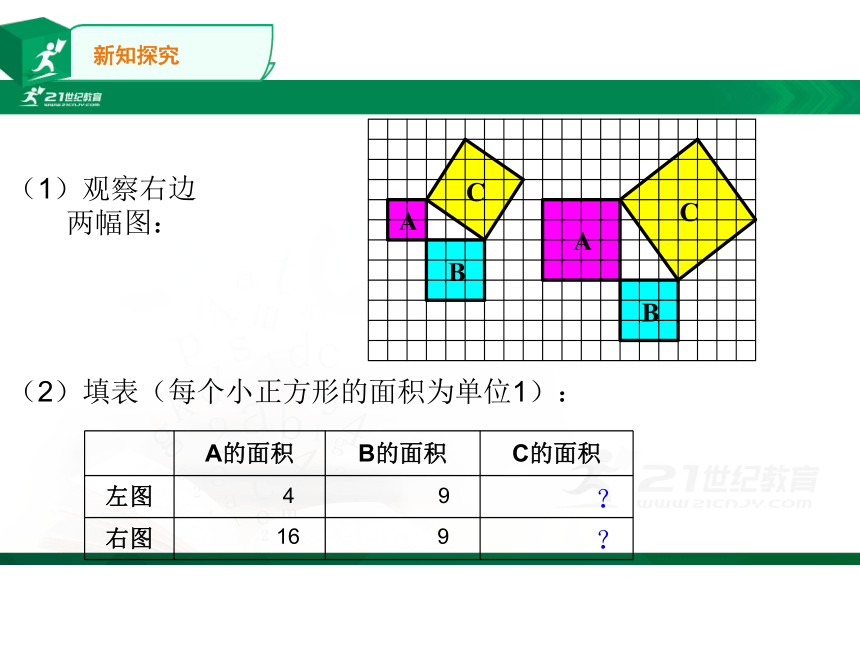
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
?
?
新知探究
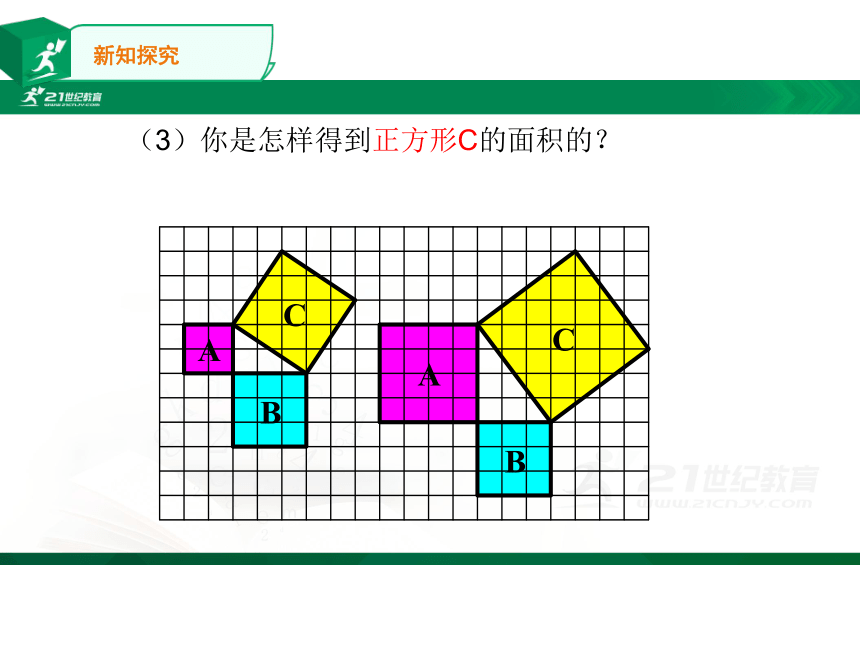
(3)你是怎样得到正方形C的面积的?
新知探究
C
B
C
A
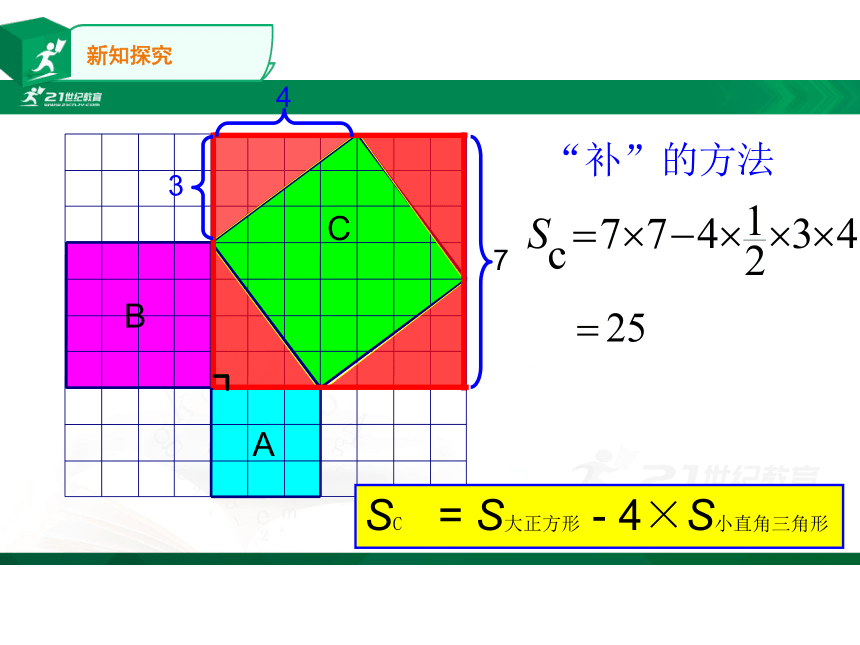
7
3
4
“补”的方法
SC
=
S大正方形
-
4×S小直角三角形
新知探究
C
B
C
A
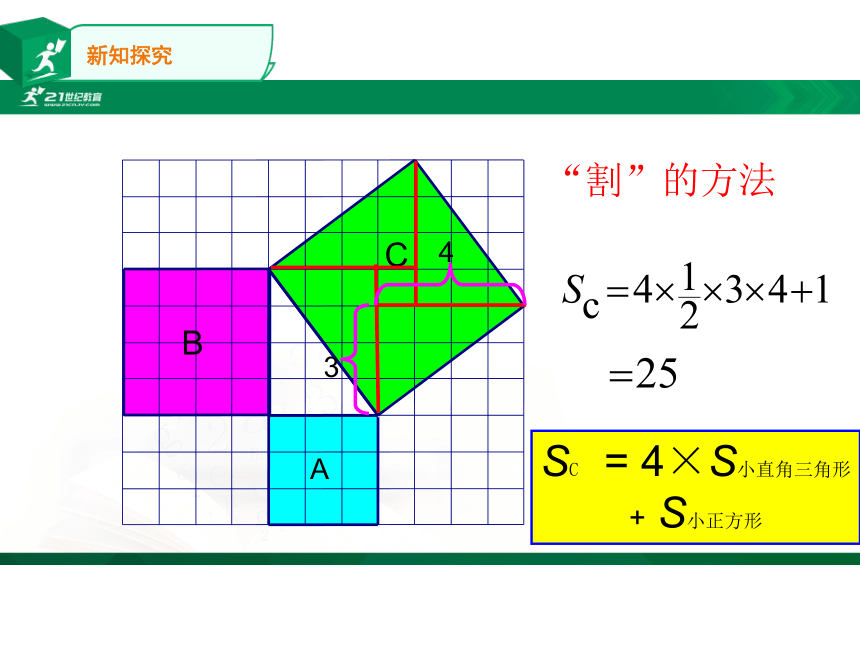
“割”的方法
3
4
SC
=
4×S小直角三角形
+
S小正方形
新知探究
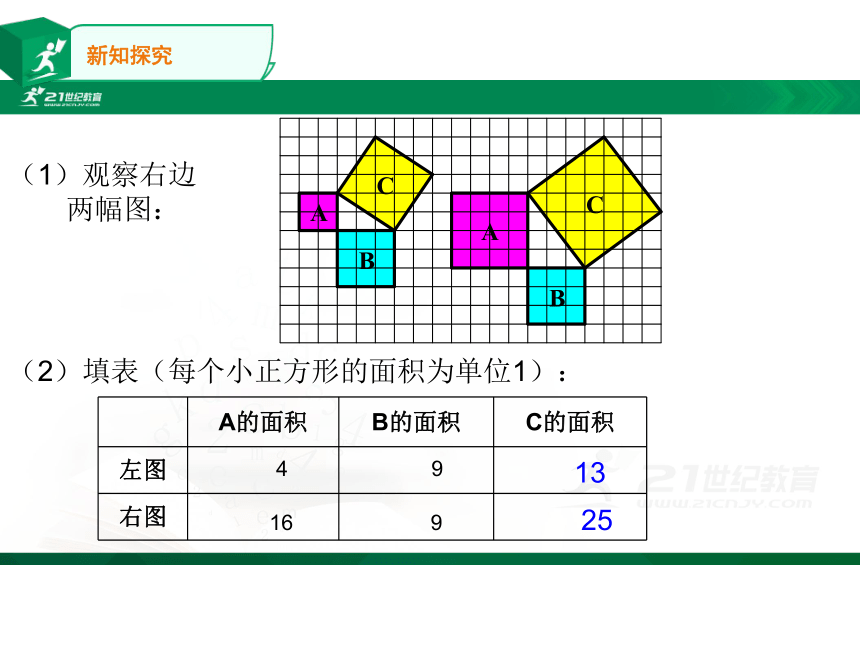
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
13
25
新知探究
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
13
25
根据表中数据,你得到了什么?
结论
新知探究
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
A
B
C
C
B
A
新知探究
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
新知探究
如果直角三角形两直角边分别为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方。
a
b
c
表示为:Rt△ABC中,∠C=90°则
勾股定理:
定理证明
你见过这个漂亮的图案吗?
这个图案有什么意义?
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的.每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图.2002年的国际数学家大会将此图作为大会会徽.
赵爽弦图
图2
已知,如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
例题讲解
直角三角形的两条直角边的平方和等于斜边的平方。
已知,如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
例题讲解
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
图1
图2
解:
解:
1.成立条件:
在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
勾a
股b
弦c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾
股
定
理
(注意:哪条边是斜边)
知识升华
课本P24
课堂作业
1.
已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
2.
在Rt△ABC中,∠B=90°,a=3,b=4,求c.
课堂作业
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾
股
定
理
课堂小结
1、课本P28第七题;
第八题
作业布置
人教版
八年级下
17.1
勾股定理
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.注意观察,你能有什么发现?
毕达哥拉斯(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
新知导入
A
B
C
新知导入
两直角边的平方和等于斜边的平方
观察图中的三个正方形的面积有什么关系?等腰直角三角形的三边之间有什么关系?
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
SA+SB=SC
等腰直角三角形三边有什么关系?
进一步思考
是不是所有的直角三角形都是这样的关系呢?
新知探究
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
?
?
新知探究
(3)你是怎样得到正方形C的面积的?
新知探究
C
B
C
A
7
3
4
“补”的方法
SC
=
S大正方形
-
4×S小直角三角形
新知探究
C
B
C
A
“割”的方法
3
4
SC
=
4×S小直角三角形
+
S小正方形
新知探究
(1)观察右边
两幅图:
(2)填表(每个小正方形的面积为单位1):
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
13
25
新知探究
A的面积
B的面积
C的面积
左图
右图
4
9
16
9
13
25
根据表中数据,你得到了什么?
结论
新知探究
(1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?
A
B
C
C
B
A
新知探究
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
新知探究
如果直角三角形两直角边分别为a、b,斜边为c,那么
直角三角形两直角边的平方和等于斜边的平方。
a
b
c
表示为:Rt△ABC中,∠C=90°则
勾股定理:
定理证明
你见过这个漂亮的图案吗?
这个图案有什么意义?
我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的.每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图.2002年的国际数学家大会将此图作为大会会徽.
赵爽弦图
图2
已知,如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
例题讲解
直角三角形的两条直角边的平方和等于斜边的平方。
已知,如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
例题讲解
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
图1
图2
图3
图1
图2
解:
解:
1.成立条件:
在直角三角形中;
3.作用:已知直角三角形任意两边长,
求第三边长.
2.公式变形:
勾a
股b
弦c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾
股
定
理
(注意:哪条边是斜边)
知识升华
课本P24
课堂作业
1.
已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
2.
在Rt△ABC中,∠B=90°,a=3,b=4,求c.
课堂作业
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾
股
定
理
课堂小结
1、课本P28第七题;
第八题
作业布置
