17.2 一元二次方程的解法(第2课时) 公式法 课件(共24张PPT)
文档属性
| 名称 | 17.2 一元二次方程的解法(第2课时) 公式法 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 15:23:17 | ||
图片预览





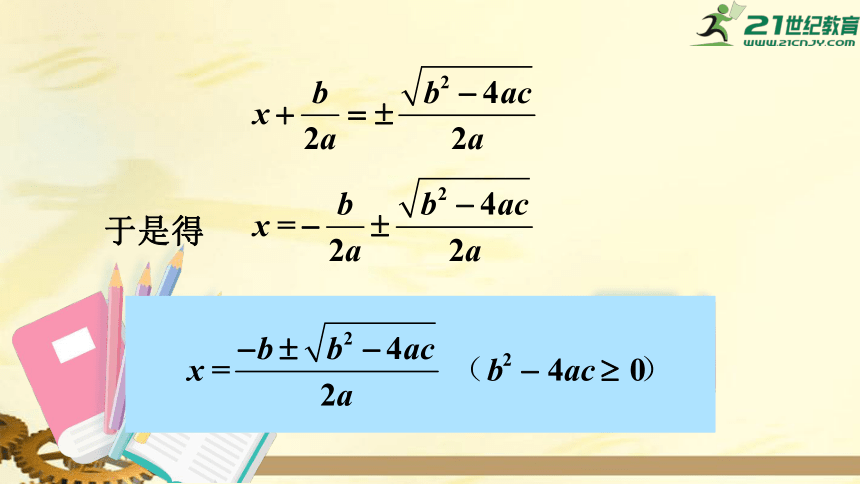



文档简介
(共24张PPT)
第
2
课时
公式法
沪科版·八年级数学下册
上课课件
第17章
一元二次方程
学习目标
【知识与技能】
掌握一元二次方程求根公式的推导,会运用公式法解一元二次方程.
【过程与方法】
1.通过求根公式的推导,培养学生数学推理的严密性及严谨性;
2.培养学生快速而准确的计算能力.
【情感态度】
1.通过公式的引入,培养学生寻求简便方法的探索精神及创新意识;
2.通过求根公式的推导,了解分类的思想.
【教学重点】
求根公式的推导及用公式法解一元二次方程.
【教学难点】
对求根公式推导过程中依据的理论的深刻理解.
新课导入
探究
如何解一般的一元二次方程
ax2
+
bx
+
c
=
0
(a
≠
0)
那么我们能否用配方法得出它的解呢?
新课探究
因为
a
≠
0,把方程两边都除以
a
,得
移项,得
配方,得
即
因为
a
≠
0,4a2
>
0.
当
b2
–
4ac
≥
0
时,
将方程
两边开平方,得
于是得
这就是一元二次方程
ax2
+
bx
+
c
=
0
(a
≠
0且
b2
–
4ac
≥
0)的求根公式.
要解一个一元二次方程,只要先把它整理成一般形式,确定出
a,b,c
的值,然后,把a,b,c
的值代入求根公式,就可以得出方程的根.
这种解法叫做公式法.
练习
把下列方程化成
ax2
+
bx
+
c
=
0
的形式,并写出其中
a,b,c
的值:
(1)x2
–
5x
=
2;
(2)3x2
–
1
=
2x
x2
–
5x
–
2
=
0
a
=
1,b
=
–5,c
=
–2
3x2
–
2x
–
1
=
0
a
=
3,b
=
–2,c
=
–1
(3)2x(x
–
1)=
x
+
4
(4)(x
+
1)2
=
3x
–
2
2x2
–
3x
–
4
=
0
a
=
2,b
=
–3,c
=
–4
x2
–
x
+
3
=
0
a
=
1,b
=
–1,c
=
3
例2
用公式法解下列方程:
(1)2x2
+
7x
–
4
=
0;(2)x2
+
3
=
.
解(1)a
=
2,b
=
7,c
=
–4,
b2
–
4ac
=
72
–
4×2×(–4)=
81
>
0.
代入求根公式,得
∴x1
=
,x2
=
–4.
(2)将原方程化为标准形式,得
x2
–
+
3
=
0.
a
=
1,b
=
,c
=
3,
b2
–
4ac
=
–
4×1×3
=
0.
代入求根公式,得
∴x1
=
x2
=
.
例3
解方程:x2
+
x
–
1
=
0(精确到0.001)
解
a
=
1,b
=
1,c
=
–1,代入求根公式,得
用计算器求得
≈
2.2361.
∴
x1
≈
0.618,x2
≈
–1.618
.
用公式法解一元二次方程的一般步骤:
把方程化为一般形式,写出
a,b,c
的值.
求出
b2
–
4ac
的值.
代入求根公式.
写出方程的解.
随堂演练
1.
利用求根公式求
5x2
+
=
6x
的根时,a,b,c
的值分别是(
)
C
A.
5,
,6
B.
5,6,
C.
5
,–6,
D.
5,–6,
2.用公式法解下列方程:
(1)x2
+
x
–
12
=
0;
(2)x2
+
4x
+
8
=
2x
+
11;
解:a
=
1,b
=
1,c
=
-12
b2
–
4ac
=
12
–
4×1×(–12)
=
49
>
0
解:化简,得
x2
+
2x
–
3
=
0
a
=
1,b
=
2,c
=
–3
b2
–
4ac
=
22
–
4×1×(–3)
=
16
>
0
3.
若方程
x2
–
9x
+
18
=
0
的两个根分别是等腰三角形的底和腰的长,则这个三角形的周长为(
)
A.
12
B.
15
C.
12或15
D.无法确定
B
4.
在正数范围内有一种运算“
”,其运算规则为
a
b
=
a
+
b2.
根据这个规则,方程
x
(x
+
1)=
5
的根为(
)
A.
x
=
5
B.
x
=
1
C.
x
=
4
D.
x1
=
–
4,x2
=
1
B
5.
已知关于
x
的一元二次方程
mx2
–(3m
–
1)x
+
2m
–
1
=
0,其根的判别式
b2
–
4ac
的值为
1,求
m
的值及方程的根.
解
b2
–
4ac
=(3m
–
1)2
–
4×m×(2m
–
1)
=
m2
–
2m
+
1
∵m2
–
2m
+1
=
1
∴
m1
=
2,m2
=
0(舍去)
原方程可化为
2x2
–
5x
+
3
=
0
a
=2,b
=
–
5,
c
=
3,代入求根公式,得
∴
x1
=
1,x2
=
.
课堂小结
ax2
+
bx
+
c
=
0
(a
≠
0且b2
–
4ac≥0)
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第
2
课时
公式法
沪科版·八年级数学下册
上课课件
第17章
一元二次方程
学习目标
【知识与技能】
掌握一元二次方程求根公式的推导,会运用公式法解一元二次方程.
【过程与方法】
1.通过求根公式的推导,培养学生数学推理的严密性及严谨性;
2.培养学生快速而准确的计算能力.
【情感态度】
1.通过公式的引入,培养学生寻求简便方法的探索精神及创新意识;
2.通过求根公式的推导,了解分类的思想.
【教学重点】
求根公式的推导及用公式法解一元二次方程.
【教学难点】
对求根公式推导过程中依据的理论的深刻理解.
新课导入
探究
如何解一般的一元二次方程
ax2
+
bx
+
c
=
0
(a
≠
0)
那么我们能否用配方法得出它的解呢?
新课探究
因为
a
≠
0,把方程两边都除以
a
,得
移项,得
配方,得
即
因为
a
≠
0,4a2
>
0.
当
b2
–
4ac
≥
0
时,
将方程
两边开平方,得
于是得
这就是一元二次方程
ax2
+
bx
+
c
=
0
(a
≠
0且
b2
–
4ac
≥
0)的求根公式.
要解一个一元二次方程,只要先把它整理成一般形式,确定出
a,b,c
的值,然后,把a,b,c
的值代入求根公式,就可以得出方程的根.
这种解法叫做公式法.
练习
把下列方程化成
ax2
+
bx
+
c
=
0
的形式,并写出其中
a,b,c
的值:
(1)x2
–
5x
=
2;
(2)3x2
–
1
=
2x
x2
–
5x
–
2
=
0
a
=
1,b
=
–5,c
=
–2
3x2
–
2x
–
1
=
0
a
=
3,b
=
–2,c
=
–1
(3)2x(x
–
1)=
x
+
4
(4)(x
+
1)2
=
3x
–
2
2x2
–
3x
–
4
=
0
a
=
2,b
=
–3,c
=
–4
x2
–
x
+
3
=
0
a
=
1,b
=
–1,c
=
3
例2
用公式法解下列方程:
(1)2x2
+
7x
–
4
=
0;(2)x2
+
3
=
.
解(1)a
=
2,b
=
7,c
=
–4,
b2
–
4ac
=
72
–
4×2×(–4)=
81
>
0.
代入求根公式,得
∴x1
=
,x2
=
–4.
(2)将原方程化为标准形式,得
x2
–
+
3
=
0.
a
=
1,b
=
,c
=
3,
b2
–
4ac
=
–
4×1×3
=
0.
代入求根公式,得
∴x1
=
x2
=
.
例3
解方程:x2
+
x
–
1
=
0(精确到0.001)
解
a
=
1,b
=
1,c
=
–1,代入求根公式,得
用计算器求得
≈
2.2361.
∴
x1
≈
0.618,x2
≈
–1.618
.
用公式法解一元二次方程的一般步骤:
把方程化为一般形式,写出
a,b,c
的值.
求出
b2
–
4ac
的值.
代入求根公式.
写出方程的解.
随堂演练
1.
利用求根公式求
5x2
+
=
6x
的根时,a,b,c
的值分别是(
)
C
A.
5,
,6
B.
5,6,
C.
5
,–6,
D.
5,–6,
2.用公式法解下列方程:
(1)x2
+
x
–
12
=
0;
(2)x2
+
4x
+
8
=
2x
+
11;
解:a
=
1,b
=
1,c
=
-12
b2
–
4ac
=
12
–
4×1×(–12)
=
49
>
0
解:化简,得
x2
+
2x
–
3
=
0
a
=
1,b
=
2,c
=
–3
b2
–
4ac
=
22
–
4×1×(–3)
=
16
>
0
3.
若方程
x2
–
9x
+
18
=
0
的两个根分别是等腰三角形的底和腰的长,则这个三角形的周长为(
)
A.
12
B.
15
C.
12或15
D.无法确定
B
4.
在正数范围内有一种运算“
”,其运算规则为
a
b
=
a
+
b2.
根据这个规则,方程
x
(x
+
1)=
5
的根为(
)
A.
x
=
5
B.
x
=
1
C.
x
=
4
D.
x1
=
–
4,x2
=
1
B
5.
已知关于
x
的一元二次方程
mx2
–(3m
–
1)x
+
2m
–
1
=
0,其根的判别式
b2
–
4ac
的值为
1,求
m
的值及方程的根.
解
b2
–
4ac
=(3m
–
1)2
–
4×m×(2m
–
1)
=
m2
–
2m
+
1
∵m2
–
2m
+1
=
1
∴
m1
=
2,m2
=
0(舍去)
原方程可化为
2x2
–
5x
+
3
=
0
a
=2,b
=
–
5,
c
=
3,代入求根公式,得
∴
x1
=
1,x2
=
.
课堂小结
ax2
+
bx
+
c
=
0
(a
≠
0且b2
–
4ac≥0)
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
