17.4 一元二次方程的根与系数的关系 课件(共23张PPT)
文档属性
| 名称 | 17.4 一元二次方程的根与系数的关系 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 15:29:02 | ||
图片预览





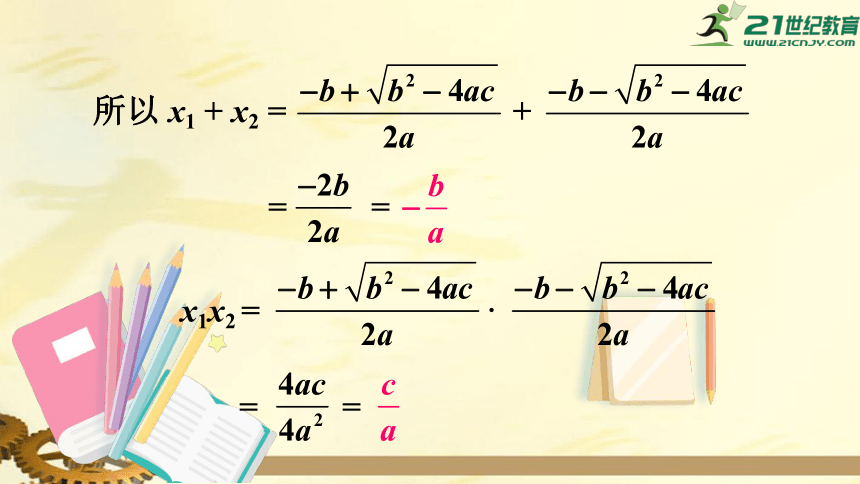


文档简介
(共23张PPT)
17.4
一元二次方程的根与系数的关系
沪科版·八年级数学下册
上课课件
第17章
一元二次方程
学习目标
【知识与技能】
1.掌握一元二次方程的根与系数的关系并会初步应用;
2.灵活运用一元二次方程根与系数关系解决实际问题.
【过程与方法】
培养学生分析、观察、归纳的能力和推理论证的能力.
【情感态度】
1.渗透由特殊到一般,再由一般到特殊的认识事物的规律;2.培养学生去发现规律的积极性及勇于探索的精神.
【教学重点】
根与系数的关系及其推导.
【教学难点】
正确理解根与系数的关系.一元二次方程根与系数的关系是指一元二次方程两根的和,两根的积与系数的关系.
新课导入
探究
你是否注意到每个方程中的两根之间的关系?两根之和(x1
+
x2)、两根之积(x1x2)与该方程的各项系数之间有怎样的关系?填写下表,然后观察根与系数的关系:
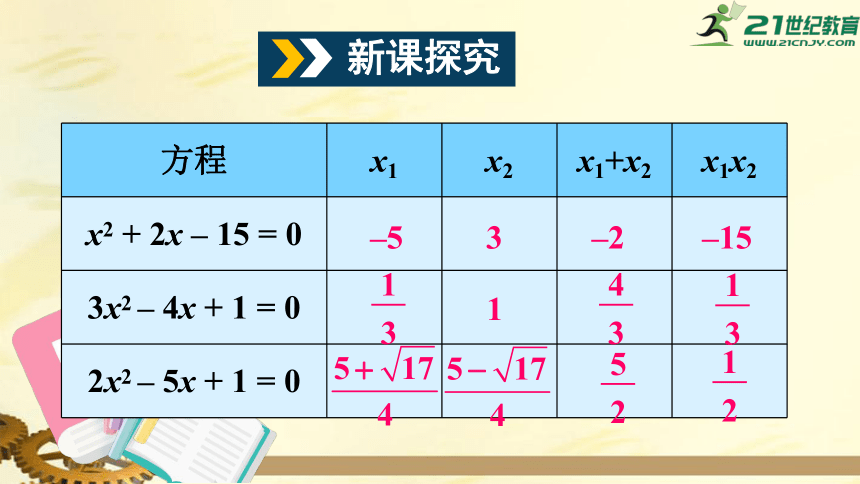
新课探究
方程
x1
x2
x1+x2
x1x2
x2
+
2x
–
15
=
0
3x2
–
4x
+
1
=
0
2x2
–
5x
+
1
=
0
–5
3
–2
–15
1
3
1
4
3
1
3
5
2
1
2
猜想:方程
ax2
+
bx
+
c
=
0(a
≠
0)的根如果是
x1、x2,那么
x1+x2
=_____,x1x2
=_____.
你能证你的猜想吗?
我们知道,一元二次方
ax2+
bx
+
c
=
0
(a
≠
0)的两根为
所以
x1
+
x2
=
+
=
=
x1x2
=
·
=
=
如果
ax2+
bx
+
c
=
0(a
≠
0)的两根为
x1,x2,
那么
x1
+
x2
=
,
x1x2
=
.
韦
达
定
理
当一元二次方程的二次项系数为
1
时,它的标准形式为
x2
+
px
+
q
=
0.
设它的两个根为
x1,x2,这时韦达定理应是:x1
+
x2
=
–p,x1x2
=
q.
练习
不解方程,求下列方程两根的和与积.
x2
–
3x
=
15;
5x2
–
1
=
4x2
+
x
解:x1
+
x2
=
3
x1x2
=
–15
解:化简得
x2
–
x
–
1
=
0
x1
+
x2
=
1
x1x2
=
–1
例
1
已知关于
x
的方程
2x2
+
kx
–
4
=
0
的一个根是
–4,求它的另一个根及
k
的值.
解
设方程的另一个根是
x2,则
解方程组,得
答:方程的另一个根为
,k
的值为
7.
想一想
本题还有别的解法吗?
解
将
x
=
–4
代入方程,得
2×(
–4
)2
+(
–4
)k
–
4
=
0.
解得
k
=
7.
将
k
=
7代入方程,得
2x2
+
7x
–
4
=
0,
解得
例
2
方程
2x2
–
3x
+
1
=
0
的两个根记作x1,x2,不解方程,求
x1
–
x2
的值.
解
由韦达定理,得
x1
+
x2
=
,
x1x2
=
.
(x1
–
x2)2
=(x1
+
x2)2
–
4x1x2
∴
x1
–
x2
=
引申:若
ax2
?
bx
?
c
?
0(a
?
0
?
?
0)
(1)若两根互为相反数,则
b
?
0;
(2)若两根互为倒数,则
a
?
c;
(3)若一根为
0,则
c
?
0;
(4)若一根为
1,则
a
?
b
?
c
?
0;
(5)若一根为
?1,则
a
?
b
?
c
?
0;
(6)若
a、c
异号,方程一定有两个实数根.
随堂演练
1.
关于
x
的方程
x2
+
px
+
q
=
0
的根为
x1
=
1+
,x2
=
1
–
,则
p
=
,q=
.
2.
已知方程
5x2
+
kx
–
6
=
0
的一根是
2,则另一根是
,
k=
.
–2
–1
–7
3.
求下列方程的两根
x1,x2
的和与积:
(1)x2
–
3x
+
2
=
0;
(2)x2
+
x
=
5x
+
6
解:x1
+
x2
=
3
x1x2
=
2
解:化简得
x2
–
4x
–
6
=
0
x1
+
x2
=
4
x1x2
=
–
6
4.
x1,x2
是方程
x2
–
5x
–
7
=
0
的两根,不解方程求下列各式的值:
(1)
;(2)
.
解:∵
x1,x2
是方程
x2
–
5x
–
7
=
0
的两根.
则
x1
+
x2
=
5,x1x2
=
–
7
.
5.
已知关于
x
的方程
x2
–(2m
+
3)x
+
m2
=
0
的两根之和等于两根之积,求
m
的值.
解:设方程
x2
–
(2m
+
3)x
+
m2
=
0
的两根为
x1,x2.
∴
x1
+
x2
=
2m
+
3,x1x2
=
m2.
根据题意得
m2
=
2m
+3,解得
m1=
3,m2
=
–
1.
当
m
=
3
时,原方程为
x2
–
9x
+
9
=
0,
b2
–
4ac
=
45
>
0.
方程有实数根.
当
m
=
–1
时,原方程为
x2
–
x
+
1
=
0,
b2
–
4ac
=
–
3
<
0.
方程无实数根,此
m
值舍去.
∴
m
的值为
3.
课堂小结
如果
ax2+
bx
+
c
=
0(a
≠
0)的两根为
x1,x2,
那么
x1+x2
=
,
x1x2
=
.
韦
达
定
理
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
17.4
一元二次方程的根与系数的关系
沪科版·八年级数学下册
上课课件
第17章
一元二次方程
学习目标
【知识与技能】
1.掌握一元二次方程的根与系数的关系并会初步应用;
2.灵活运用一元二次方程根与系数关系解决实际问题.
【过程与方法】
培养学生分析、观察、归纳的能力和推理论证的能力.
【情感态度】
1.渗透由特殊到一般,再由一般到特殊的认识事物的规律;2.培养学生去发现规律的积极性及勇于探索的精神.
【教学重点】
根与系数的关系及其推导.
【教学难点】
正确理解根与系数的关系.一元二次方程根与系数的关系是指一元二次方程两根的和,两根的积与系数的关系.
新课导入
探究
你是否注意到每个方程中的两根之间的关系?两根之和(x1
+
x2)、两根之积(x1x2)与该方程的各项系数之间有怎样的关系?填写下表,然后观察根与系数的关系:
新课探究
方程
x1
x2
x1+x2
x1x2
x2
+
2x
–
15
=
0
3x2
–
4x
+
1
=
0
2x2
–
5x
+
1
=
0
–5
3
–2
–15
1
3
1
4
3
1
3
5
2
1
2
猜想:方程
ax2
+
bx
+
c
=
0(a
≠
0)的根如果是
x1、x2,那么
x1+x2
=_____,x1x2
=_____.
你能证你的猜想吗?
我们知道,一元二次方
ax2+
bx
+
c
=
0
(a
≠
0)的两根为
所以
x1
+
x2
=
+
=
=
x1x2
=
·
=
=
如果
ax2+
bx
+
c
=
0(a
≠
0)的两根为
x1,x2,
那么
x1
+
x2
=
,
x1x2
=
.
韦
达
定
理
当一元二次方程的二次项系数为
1
时,它的标准形式为
x2
+
px
+
q
=
0.
设它的两个根为
x1,x2,这时韦达定理应是:x1
+
x2
=
–p,x1x2
=
q.
练习
不解方程,求下列方程两根的和与积.
x2
–
3x
=
15;
5x2
–
1
=
4x2
+
x
解:x1
+
x2
=
3
x1x2
=
–15
解:化简得
x2
–
x
–
1
=
0
x1
+
x2
=
1
x1x2
=
–1
例
1
已知关于
x
的方程
2x2
+
kx
–
4
=
0
的一个根是
–4,求它的另一个根及
k
的值.
解
设方程的另一个根是
x2,则
解方程组,得
答:方程的另一个根为
,k
的值为
7.
想一想
本题还有别的解法吗?
解
将
x
=
–4
代入方程,得
2×(
–4
)2
+(
–4
)k
–
4
=
0.
解得
k
=
7.
将
k
=
7代入方程,得
2x2
+
7x
–
4
=
0,
解得
例
2
方程
2x2
–
3x
+
1
=
0
的两个根记作x1,x2,不解方程,求
x1
–
x2
的值.
解
由韦达定理,得
x1
+
x2
=
,
x1x2
=
.
(x1
–
x2)2
=(x1
+
x2)2
–
4x1x2
∴
x1
–
x2
=
引申:若
ax2
?
bx
?
c
?
0(a
?
0
?
?
0)
(1)若两根互为相反数,则
b
?
0;
(2)若两根互为倒数,则
a
?
c;
(3)若一根为
0,则
c
?
0;
(4)若一根为
1,则
a
?
b
?
c
?
0;
(5)若一根为
?1,则
a
?
b
?
c
?
0;
(6)若
a、c
异号,方程一定有两个实数根.
随堂演练
1.
关于
x
的方程
x2
+
px
+
q
=
0
的根为
x1
=
1+
,x2
=
1
–
,则
p
=
,q=
.
2.
已知方程
5x2
+
kx
–
6
=
0
的一根是
2,则另一根是
,
k=
.
–2
–1
–7
3.
求下列方程的两根
x1,x2
的和与积:
(1)x2
–
3x
+
2
=
0;
(2)x2
+
x
=
5x
+
6
解:x1
+
x2
=
3
x1x2
=
2
解:化简得
x2
–
4x
–
6
=
0
x1
+
x2
=
4
x1x2
=
–
6
4.
x1,x2
是方程
x2
–
5x
–
7
=
0
的两根,不解方程求下列各式的值:
(1)
;(2)
.
解:∵
x1,x2
是方程
x2
–
5x
–
7
=
0
的两根.
则
x1
+
x2
=
5,x1x2
=
–
7
.
5.
已知关于
x
的方程
x2
–(2m
+
3)x
+
m2
=
0
的两根之和等于两根之积,求
m
的值.
解:设方程
x2
–
(2m
+
3)x
+
m2
=
0
的两根为
x1,x2.
∴
x1
+
x2
=
2m
+
3,x1x2
=
m2.
根据题意得
m2
=
2m
+3,解得
m1=
3,m2
=
–
1.
当
m
=
3
时,原方程为
x2
–
9x
+
9
=
0,
b2
–
4ac
=
45
>
0.
方程有实数根.
当
m
=
–1
时,原方程为
x2
–
x
+
1
=
0,
b2
–
4ac
=
–
3
<
0.
方程无实数根,此
m
值舍去.
∴
m
的值为
3.
课堂小结
如果
ax2+
bx
+
c
=
0(a
≠
0)的两根为
x1,x2,
那么
x1+x2
=
,
x1x2
=
.
韦
达
定
理
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
