17.5 一元二次方程的应用(第2课时) 面积问题与其他问题 课件(共20张PPT)
文档属性
| 名称 | 17.5 一元二次方程的应用(第2课时) 面积问题与其他问题 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第2课时
面积问题与其他问题
沪科版·八年级数学下册
上课课件
第17章
一元二次方程
学习目标
【知识与技能】
本节课使学生掌握可化为一元二次方程的分式方程的解法,能用去分母的方法或换元的方法求此类方程的解,并会验根.
【过程与方法】
1.使学生掌握运用去分母或换元的方法解可化为一元二次方程的分式方程;使学生理解转化的数学基本思想;
2.使学生能够利用最简公分母进行验根.
【情感态度】
结合对题目的分析与解答,对学生进行辩证唯物主义思想的教育.
【教学重点】
掌握可化为一元二次方程的分式方程的解法.
【教学难点】
解分式方程,学生不容易理解为什么必须进行检验.学生容易忽视对分式方程的解进行检验.通过对分式方程的解的剖析,进一步使学生认识解分式方程必须进行检验的重要性.
新课导入
1.怎样解分式方程:
解:(x-2)+4x-2(x+2)=x2-4
x2-3x+2=0
(x-2)
(x-1)=0
x=1或x=2
怎样进行检验?
经检验:x=1是原方程的根,
x=2是增根.
分式方程解完后一定要检验.
(舍去)
新课探究
例
4
正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高
20
cm,容积为
2
880
cm3
的开口方盒.问原金属片的边长是多少?
解
设原金属片的边长为
x
cm,则方盒的底边长是(x
–
40)cm.
根据题意,得
20(x
–
40)2
=
2880.
解方程得
x1
=
52,x2
=
28.
x2
不符合题意,所以
x
=
52.
答:原金属片的边长为
52
cm.
x
x
–
40
20
20
例
5
一组学生组织春游,预计共需费用
120
元.后来又有
2
人参加进来,费用不变,这样每人可少分摊
3
元.问原来这组学生的人数是多少?
分析:设原来这组学生的人数是
x
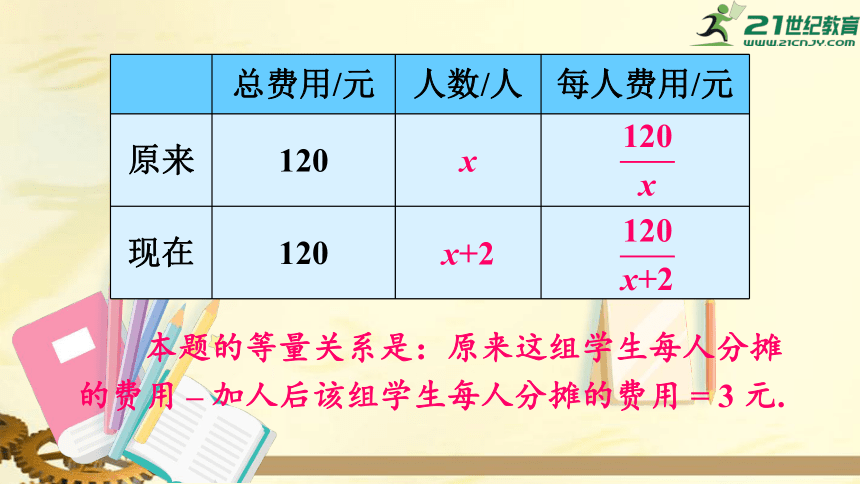
人,则把题中信息理成下表:
总费用/元
人数/人
每人费用/元
原来
120
现在
120
x
120
x
x+2
120
x+2
本题的等量关系是:原来这组学生每人分摊的费用
–
加人后该组学生每人分摊的费用
=
3
元.
解
设原来这组学生的人数是
x
人,那么每人分摊的费用是
元,增加
2
人后这组学生每人分摊的费用是
元.
根据等量关系得
120
x
120
x+2
方程两边同乘以
x(x
+
2),整理,得
x2
+
2x
–
80
=
0.
解这个方程,得
x1
=
–10(不合题意,舍去),x2
=
8.
答:原来这组学生是
8
人.
随堂演练
1.
在长方形钢片上裁掉一个长方形,制成一个四周宽相等的长方形框
.已知长方形钢片的长为
30
cm,宽为
20
cm,
要使制成的长方形框的面积为
400
cm2,求这个长方形框的边框宽?
解:设长方形框的边框宽为
x
cm
.依题意得,
(30
–
2x)(20
–
2x)
=
600
–
400
.
整理,得
x2
–
25x
+
100
=
0,
解得
x1
=
5,
x2
=
20(舍去)
.
∴
x
=
5.
答:这个长方形框的边框宽为
5
cm
.
2.
小林准备进行如下操作实验:把一根长为40
cm
的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于
58
cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于
48
cm2.”他的说法对吗?请说明理由.
解:(1)设其中一个小正方形的边长为
x
cm,则另一个小正方形的边长为(10
–
x)cm.
依题意
x2
+(10
–
x)2
=
58,
解得
x1
=
3,x2
=
7.
当
x
=
3
时,小正方形周长为
12
cm;
当
x
=
7
时,小正方形周长为
28
cm.
∴小林应把长为
40
cm
的铁丝剪为
28
cm
和
12
cm
的两段.
(2)对.两个正方形的面积之和为:
x2
+(10
–
x)2
=
2x2
–
20x
+
100
=2(x2
–
10x
+
25)+
50
=2(x
–
5)2
+
50
∵无论
x
取何值,2(x
–
5)2
总是不小于
0
的.
∴2(x
–
5)2
+
50
≥
50.
即这两个正方形的面积之和总是不小于
50
cm2
的,所以不可能等于
48
cm2.
小峰的说法是对的.
3.
如图,要设计一幅宽
20
cm,长30
cm
的图案,其中有两横、两竖的彩条,横、竖彩条的宽度比为
3∶2,如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)?
③
④
①
②
解:设横彩条的宽度为
3x
cm.则竖彩条的宽度为
2x
cm.
根据题意,得
30×20×
=30×20
–(30
–
4x)(20
–
6x).
整理,得
12x2
–
130x
+
75
=
0.
解得
x1
=
,
x2
=
.
∵
30
–
4x
>
0
且
20
–
6x
>
0.∴
x
<
.∴x
=
舍去.
∴
x
=
≈
0.6
.
∴
3x
≈
1.8,
2x
≈
1.2.
答:横彩条的宽度约为
1.8
cm,竖彩条的宽度约为
1.2
cm.
课堂小结
分式方程解题步骤:
(1)将分式方程通过去分母转化为整式方程求解;
(2)解分式方程一定要检验;
(3)要根据实际情况将不符合实际的解舍去.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第2课时
面积问题与其他问题
沪科版·八年级数学下册
上课课件
第17章
一元二次方程
学习目标
【知识与技能】
本节课使学生掌握可化为一元二次方程的分式方程的解法,能用去分母的方法或换元的方法求此类方程的解,并会验根.
【过程与方法】
1.使学生掌握运用去分母或换元的方法解可化为一元二次方程的分式方程;使学生理解转化的数学基本思想;
2.使学生能够利用最简公分母进行验根.
【情感态度】
结合对题目的分析与解答,对学生进行辩证唯物主义思想的教育.
【教学重点】
掌握可化为一元二次方程的分式方程的解法.
【教学难点】
解分式方程,学生不容易理解为什么必须进行检验.学生容易忽视对分式方程的解进行检验.通过对分式方程的解的剖析,进一步使学生认识解分式方程必须进行检验的重要性.
新课导入
1.怎样解分式方程:
解:(x-2)+4x-2(x+2)=x2-4
x2-3x+2=0
(x-2)
(x-1)=0
x=1或x=2
怎样进行检验?
经检验:x=1是原方程的根,
x=2是增根.
分式方程解完后一定要检验.
(舍去)
新课探究
例
4
正方形金属片一块,将其四个角各截去一个相同大小的小正方形,围成高
20
cm,容积为
2
880
cm3
的开口方盒.问原金属片的边长是多少?
解
设原金属片的边长为
x
cm,则方盒的底边长是(x
–
40)cm.
根据题意,得
20(x
–
40)2
=
2880.
解方程得
x1
=
52,x2
=
28.
x2
不符合题意,所以
x
=
52.
答:原金属片的边长为
52
cm.
x
x
–
40
20
20
例
5
一组学生组织春游,预计共需费用
120
元.后来又有
2
人参加进来,费用不变,这样每人可少分摊
3
元.问原来这组学生的人数是多少?
分析:设原来这组学生的人数是
x
人,则把题中信息理成下表:
总费用/元
人数/人
每人费用/元
原来
120
现在
120
x
120
x
x+2
120
x+2
本题的等量关系是:原来这组学生每人分摊的费用
–
加人后该组学生每人分摊的费用
=
3
元.
解
设原来这组学生的人数是
x
人,那么每人分摊的费用是
元,增加
2
人后这组学生每人分摊的费用是
元.
根据等量关系得
120
x
120
x+2
方程两边同乘以
x(x
+
2),整理,得
x2
+
2x
–
80
=
0.
解这个方程,得
x1
=
–10(不合题意,舍去),x2
=
8.
答:原来这组学生是
8
人.
随堂演练
1.
在长方形钢片上裁掉一个长方形,制成一个四周宽相等的长方形框
.已知长方形钢片的长为
30
cm,宽为
20
cm,
要使制成的长方形框的面积为
400
cm2,求这个长方形框的边框宽?
解:设长方形框的边框宽为
x
cm
.依题意得,
(30
–
2x)(20
–
2x)
=
600
–
400
.
整理,得
x2
–
25x
+
100
=
0,
解得
x1
=
5,
x2
=
20(舍去)
.
∴
x
=
5.
答:这个长方形框的边框宽为
5
cm
.
2.
小林准备进行如下操作实验:把一根长为40
cm
的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于
58
cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于
48
cm2.”他的说法对吗?请说明理由.
解:(1)设其中一个小正方形的边长为
x
cm,则另一个小正方形的边长为(10
–
x)cm.
依题意
x2
+(10
–
x)2
=
58,
解得
x1
=
3,x2
=
7.
当
x
=
3
时,小正方形周长为
12
cm;
当
x
=
7
时,小正方形周长为
28
cm.
∴小林应把长为
40
cm
的铁丝剪为
28
cm
和
12
cm
的两段.
(2)对.两个正方形的面积之和为:
x2
+(10
–
x)2
=
2x2
–
20x
+
100
=2(x2
–
10x
+
25)+
50
=2(x
–
5)2
+
50
∵无论
x
取何值,2(x
–
5)2
总是不小于
0
的.
∴2(x
–
5)2
+
50
≥
50.
即这两个正方形的面积之和总是不小于
50
cm2
的,所以不可能等于
48
cm2.
小峰的说法是对的.
3.
如图,要设计一幅宽
20
cm,长30
cm
的图案,其中有两横、两竖的彩条,横、竖彩条的宽度比为
3∶2,如果要使彩条所占面积是图案面积的四分之一,应如何设计彩条的宽度(结果保留小数点后一位)?
③
④
①
②
解:设横彩条的宽度为
3x
cm.则竖彩条的宽度为
2x
cm.
根据题意,得
30×20×
=30×20
–(30
–
4x)(20
–
6x).
整理,得
12x2
–
130x
+
75
=
0.
解得
x1
=
,
x2
=
.
∵
30
–
4x
>
0
且
20
–
6x
>
0.∴
x
<
.∴x
=
舍去.
∴
x
=
≈
0.6
.
∴
3x
≈
1.8,
2x
≈
1.2.
答:横彩条的宽度约为
1.8
cm,竖彩条的宽度约为
1.2
cm.
课堂小结
分式方程解题步骤:
(1)将分式方程通过去分母转化为整式方程求解;
(2)解分式方程一定要检验;
(3)要根据实际情况将不符合实际的解舍去.
1.从教材习题中选取,
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
