新人教版九年级下 27.2.1相似三角形的判定3
文档属性
| 名称 | 新人教版九年级下 27.2.1相似三角形的判定3 |
|
|
| 格式 | rar | ||
| 文件大小 | 543.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-08 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
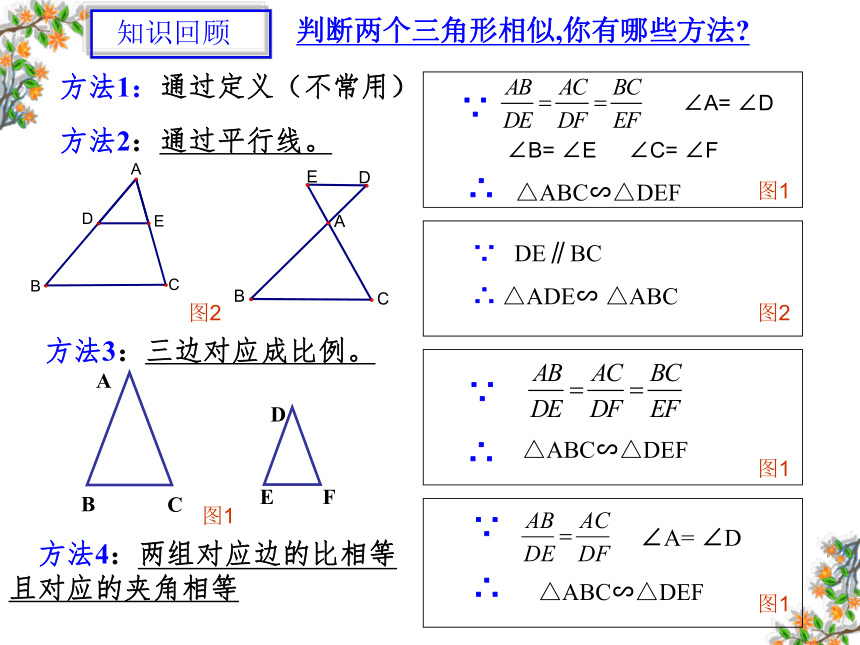
判断两个三角形相似,你有哪些方法
方法1:通过定义(不常用)
方法2:通过平行线。
∵ DE∥BC
∴ △ADE∽ △ABC
方法3:三边对应成比例。
方法4:两组对应边的比相等 且对应的夹角相等
∠A= ∠D
△ABC∽△DEF
∵
∴
D
E
F
B
A
C
知识回顾
△ABC∽△DEF
∵
∴
∠A= ∠D
∠B= ∠E
∠C= ∠F
△ABC∽△DEF
∴
∵
图1
图1
图1
图1
图2
图2
27.2.1相似三角形的判定3
相似三角形判定3
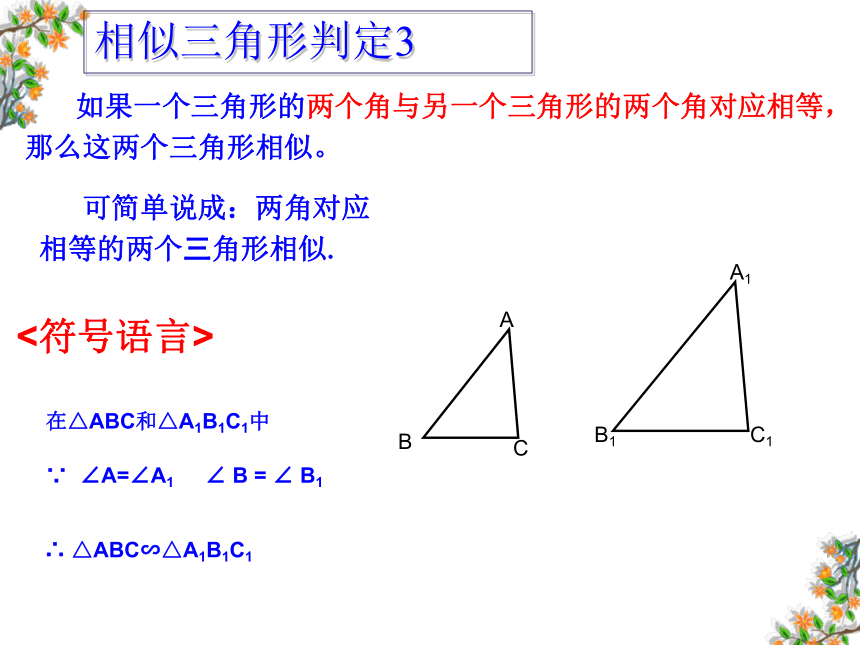
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
可简单说成:两角对应相等的两个三角形相似.
<符号语言>
A
B
C
A1
B1
C1
∴ △ABC∽△A1B1C1
∠A=∠A1 ∠ B = ∠ B1
在△ABC和△A1B1C1中
∵
已知:
求证:
证明:
△ABC 和 △A1B1C1 中,∠A=∠A1,∠B=∠B1
△ABC ∽ △A1B1C1
∵ DE ‖ B1C1
∴ ∠A1D E = ∠B1
△A1D E ∽ △A1B1C1
又∠B = ∠B1
∴∠B = ∠A1DE
在△A1D E △A1B1C1中
∠A = ∠A1,
A1D = AB
∠B = ∠A1DE
∴△A1D E ≌ △ABC(ASA)
∴△ABC ∽ △A1B1C1
A
B
C
A1
B1
C1
D
E
在线段 A1B1 上截取 A1D=AB,过点 D 作 DE‖B1C1,交A1C1于点E,
D
E
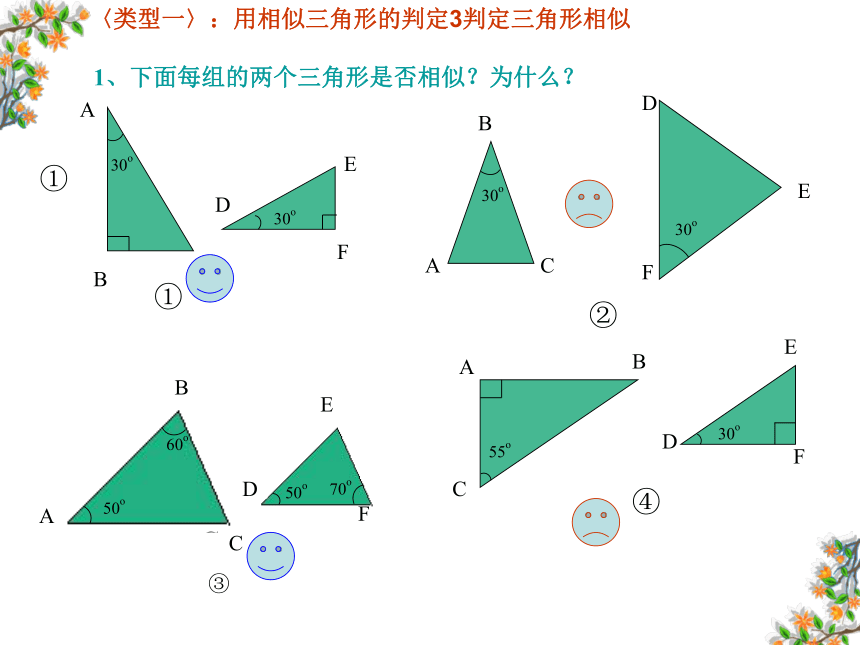
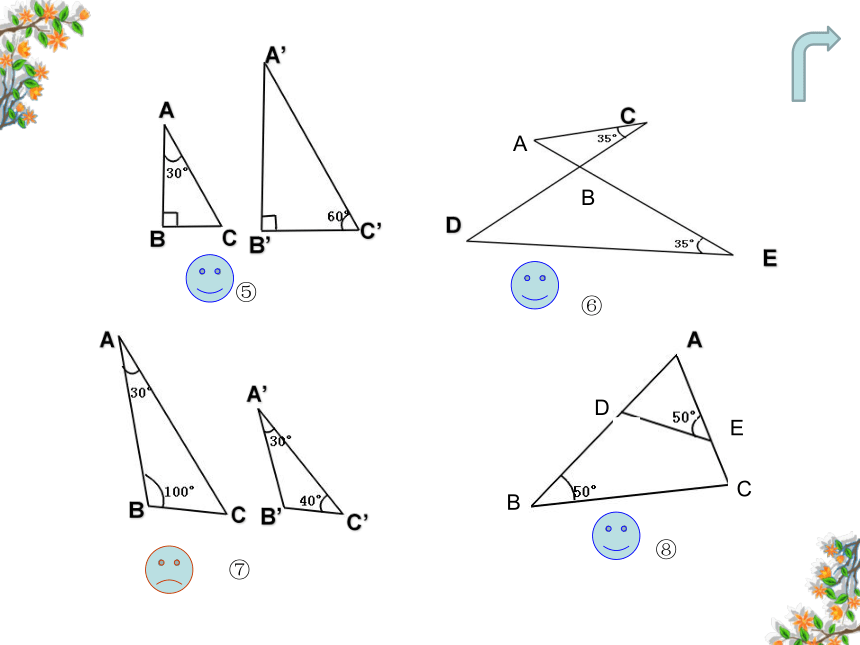
1、下面每组的两个三角形是否相似?为什么?
①
①
②
④
A
B
C
F
D
E
A
C
B
D
E
F
B
A
C
F
30o
30o
30o
30o
55o
30o
D
E
60o
50o
70o
50o
D
A
A
B
B
C
C
D
E
F
③
〈类型一〉:用相似三角形的判定3判定三角形相似
A
B
C
D
E
A
B
C
A’
C’
B’
A
B
C
A’
B’
C’
A
B
C
D
E
⑥
⑤
⑦
⑧
A
B
B
C
E
D
判断题:
2、对的打“√”,错的打“×”
1.所有的等边三角形都相似。 ( )
2.所有的直角三角形都相似。 ( )
3.所有的等腰三角形都相似。 ( )
4.所有的等腰直角三角形都相似。 ( )
×
√
×
√
5.有一个锐角相等的两直角三角形是相似三角形.( )
6.有一个角相等的两等腰三角形是相似三角形.( )
7.顶角相等的两个等腰三角形相似( )
√
×
√
3.如图,要使△ACD∽△ABC,只需要添加条件_______(只要写出一种合适的条件即可)
A
B
C
D
2
1
∠1=∠B
如图:AD是直角三角形△ABC斜边BC上的高,则
1.图中有哪些相等的角?
2.找出图中的相似三角形,并说明理由。
∠1=∠B,
∠2=∠C,
∠CAB=∠ADC= ∠ADB
△ ABC ∽△ DAC ∽△ DBA
4例题、
试一试:
B
C
A
E
D
B
C
A
E
D
F
如图,AD⊥BC于点D, CE⊥AB于点 E ,且交AD于F,你能从中找出几对相似三角形?
<归纳总结>
1、对顶角相等
2、公共角
3、同(等)角的余角相等
同(等)角的补角相等
4、两直线平行,同位角相等
两直线平行,内错角相等
找对应的角 ,一般用到的找相等角的方法
5、弦AB和CD相交于⊙O内一点P,求证: PA PB=PC PD.
分析:要证PA PB=PC PD,需要证:
则需要证明这四条线段所在的两个三角形相似.
证明:连接AC、BD
∵∠CAB、∠CDB都是弧CB所对的圆周角
∴PA PB=PC PD
∴∠CAB=∠CDB
同理:∠ACD=∠ABD
∴△PAC∽△PDB
A
B
C
D
P
O
<类型二>相似三角形与圆综合应用
归纳总结 知识拓展
1、等积式
比例式
相似三角形
对应线段所在三角形
A
B
C
D
2、若 AC2=AD·AB
一般情况下,AC为两个相似三角形的公共边
则△ ACD ∽△ ABC
中考链接
1、如图,∠1=∠2,添加一个条件____________,
使得△ADE∽ △ABC
A
B
C
D
E
2
1
2、如图, △ ABC中,点D在边AB上,满足
∠ ACD= ∠ ABC,若AC=2,AD=1,则DB=___________
A
B
C
D
3
∠ D= ∠ B
课 堂 小 结
相似三角形的识别方法有那些?
方法1:通过定义
方法2:平行于三角形一边的直线。
方法3:三边对应成比例。
方法4:两边对应成比例且夹角相等。
方法5:两角对应相等。
如图,在Rt△ABC的一边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.
思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?
A
C
B
.P
A
B
C
D
E
2
1
O
C
B
A
D
A
B
C
D
E
O
C
D
A
B
A
B
C
D
E
常见相似图形
判断两个三角形相似,你有哪些方法
方法1:通过定义(不常用)
方法2:通过平行线。
∵ DE∥BC
∴ △ADE∽ △ABC
方法3:三边对应成比例。
方法4:两组对应边的比相等 且对应的夹角相等
∠A= ∠D
△ABC∽△DEF
∵
∴
D
E
F
B
A
C
知识回顾
△ABC∽△DEF
∵
∴
∠A= ∠D
∠B= ∠E
∠C= ∠F
△ABC∽△DEF
∴
∵
图1
图1
图1
图1
图2
图2
27.2.1相似三角形的判定3
相似三角形判定3
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
可简单说成:两角对应相等的两个三角形相似.
<符号语言>
A
B
C
A1
B1
C1
∴ △ABC∽△A1B1C1
∠A=∠A1 ∠ B = ∠ B1
在△ABC和△A1B1C1中
∵
已知:
求证:
证明:
△ABC 和 △A1B1C1 中,∠A=∠A1,∠B=∠B1
△ABC ∽ △A1B1C1
∵ DE ‖ B1C1
∴ ∠A1D E = ∠B1
△A1D E ∽ △A1B1C1
又∠B = ∠B1
∴∠B = ∠A1DE
在△A1D E △A1B1C1中
∠A = ∠A1,
A1D = AB
∠B = ∠A1DE
∴△A1D E ≌ △ABC(ASA)
∴△ABC ∽ △A1B1C1
A
B
C
A1
B1
C1
D
E
在线段 A1B1 上截取 A1D=AB,过点 D 作 DE‖B1C1,交A1C1于点E,
D
E
1、下面每组的两个三角形是否相似?为什么?
①
①
②
④
A
B
C
F
D
E
A
C
B
D
E
F
B
A
C
F
30o
30o
30o
30o
55o
30o
D
E
60o
50o
70o
50o
D
A
A
B
B
C
C
D
E
F
③
〈类型一〉:用相似三角形的判定3判定三角形相似
A
B
C
D
E
A
B
C
A’
C’
B’
A
B
C
A’
B’
C’
A
B
C
D
E
⑥
⑤
⑦
⑧
A
B
B
C
E
D
判断题:
2、对的打“√”,错的打“×”
1.所有的等边三角形都相似。 ( )
2.所有的直角三角形都相似。 ( )
3.所有的等腰三角形都相似。 ( )
4.所有的等腰直角三角形都相似。 ( )
×
√
×
√
5.有一个锐角相等的两直角三角形是相似三角形.( )
6.有一个角相等的两等腰三角形是相似三角形.( )
7.顶角相等的两个等腰三角形相似( )
√
×
√
3.如图,要使△ACD∽△ABC,只需要添加条件_______(只要写出一种合适的条件即可)
A
B
C
D
2
1
∠1=∠B
如图:AD是直角三角形△ABC斜边BC上的高,则
1.图中有哪些相等的角?
2.找出图中的相似三角形,并说明理由。
∠1=∠B,
∠2=∠C,
∠CAB=∠ADC= ∠ADB
△ ABC ∽△ DAC ∽△ DBA
4例题、
试一试:
B
C
A
E
D
B
C
A
E
D
F
如图,AD⊥BC于点D, CE⊥AB于点 E ,且交AD于F,你能从中找出几对相似三角形?
<归纳总结>
1、对顶角相等
2、公共角
3、同(等)角的余角相等
同(等)角的补角相等
4、两直线平行,同位角相等
两直线平行,内错角相等
找对应的角 ,一般用到的找相等角的方法
5、弦AB和CD相交于⊙O内一点P,求证: PA PB=PC PD.
分析:要证PA PB=PC PD,需要证:
则需要证明这四条线段所在的两个三角形相似.
证明:连接AC、BD
∵∠CAB、∠CDB都是弧CB所对的圆周角
∴PA PB=PC PD
∴∠CAB=∠CDB
同理:∠ACD=∠ABD
∴△PAC∽△PDB
A
B
C
D
P
O
<类型二>相似三角形与圆综合应用
归纳总结 知识拓展
1、等积式
比例式
相似三角形
对应线段所在三角形
A
B
C
D
2、若 AC2=AD·AB
一般情况下,AC为两个相似三角形的公共边
则△ ACD ∽△ ABC
中考链接
1、如图,∠1=∠2,添加一个条件____________,
使得△ADE∽ △ABC
A
B
C
D
E
2
1
2、如图, △ ABC中,点D在边AB上,满足
∠ ACD= ∠ ABC,若AC=2,AD=1,则DB=___________
A
B
C
D
3
∠ D= ∠ B
课 堂 小 结
相似三角形的识别方法有那些?
方法1:通过定义
方法2:平行于三角形一边的直线。
方法3:三边对应成比例。
方法4:两边对应成比例且夹角相等。
方法5:两角对应相等。
如图,在Rt△ABC的一边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.
思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?
A
C
B
.P
A
B
C
D
E
2
1
O
C
B
A
D
A
B
C
D
E
O
C
D
A
B
A
B
C
D
E
常见相似图形
