山东省济宁地区2011-2012学年度第一学期期末考试九年级数学试题(含答案)
文档属性
| 名称 | 山东省济宁地区2011-2012学年度第一学期期末考试九年级数学试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 129.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-08 00:00:00 | ||
图片预览




文档简介
山东省济宁地区2011—2012学年度第一学期期末考试
九年级数学试题(三年制)
题号 一 二 三 总分
16 17 18 19 20 21 22 23 24
得分
选择题答题栏
题 号 1 2 3 4 5 6 7 8 9 10
答 案
一、选择题(本大题满分30分,每小题3分.每小题只有一个符合题意的选项,请你将正确选项的代号填在答题栏内 )
1.-的值是
A.4 B. C.2 D.3
2.在等边三角形、正五边形、正六边形、正七边形中,既是轴对称图形,又是中心对称图形的是
A.等边三角形 B.正五边形 C.正六边形 D.正七边形
3.二次函数顶点坐标是
A.(-1,-2) B.(1,2) C.(-1,2) D.(0,2)
4.小红随意在如图所示的地板上踢键子,则键子恰落在黑色
方砖上的概率为
A. B. C. D.
5.如图,以O为圆心的两个同心圆中,大圆的弦是小圆的
切线.若大圆半径为,小圆半径为,则弦的长为
A.8cm B.10cm C.12cm D.16cm
6.用配方法将化成的形式为( ).
A. B.
C. D.
九年级数学试题(三年制)第1页(共8页)
7. 从甲、乙、丙、丁四人中用抽签的方式,选取二人打扫卫生,那么能同时选中甲、乙二人的概率为
A. B. C. D.
8.如图,P为⊙O外一点,PA,PB分别切⊙O于A、B,CD切
⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD
的周长为( )
A.5 B.8 C.10 D.12
9.如图,⊙O1、⊙O2相内切于点A,其半径分别是8和4,
将⊙O2沿直线O1 O2平移至两圆相外切时,则点O2移动的
长度是
A.4 B.8 C.16 D.8 或16
10.已知二次函数 y=ax2+bx+c的y与x的部分对应值如下表:
x … -1 0 1 2 …
y … -5 1 3 1 …
则下列判断中正确的是
A.该函数图象开口向上
B.该函数图象与y轴交于负半轴
C.方程ax2+bx+c=0的正根在1与2之间
D.方程ax2+bx+c=0的正根在2与3之间
二、填空题(本大题满分15分,每小题3分,请你将答案填写在题目中的横线上)
11.将抛物线y=x2的图象向上平移1个单位后,得到新的抛物线,则新的抛物线的解析式是 .
12.若正三角形的边长为6,则其内切圆的半径等于 .
13.在一个不透明的布袋中,有黄色、白色的乒乓球共10个,这些球除颜色外都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中白球的个数很可能是 个.
14.如图,分别以A,B为圆心,线段AB的长为
半径的两个圆相交于C、D两点,则∠CAD的
度数为 .
九年级数学试题(三年制)第2页(共8页)
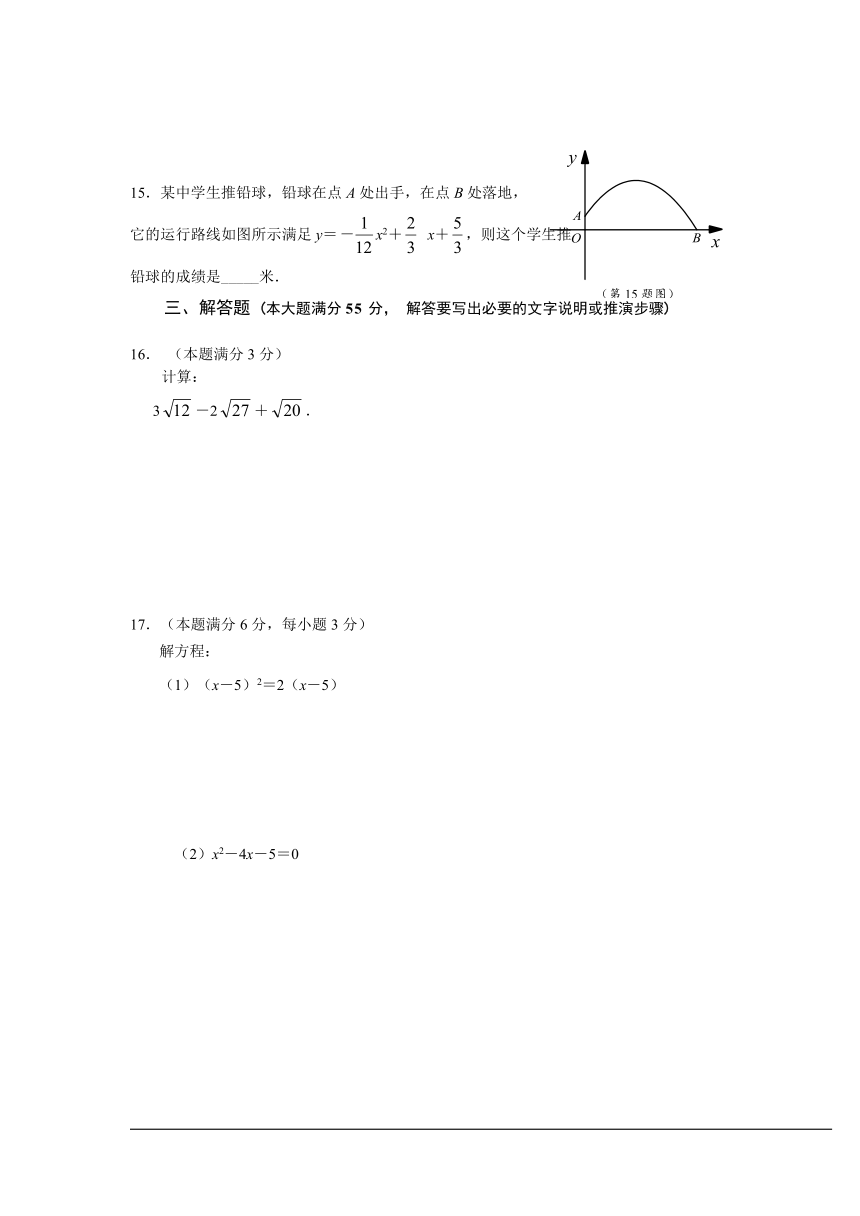
15.某中学生推铅球,铅球在点A处出手,在点B处落地,
它的运行路线如图所示满足y=-x2+ x+,则这个学生推
铅球的成绩是_____米.
三、解答题 (本大题满分55分, 解答要写出必要的文字说明或推演步骤)
16. (本题满分3分)
计算:
3-2+.
17.(本题满分6分,每小题3分)
解方程:
(1)(x-5)2=2(x-5)
(2)x2-4x-5=0
九年级数学试题(三年制)第3页(共8页)
18. (本题满分5分)
一道选择题共有A、B、C、D四个备选答案,
(1)如果其中只有一个是正确的,某位同学随意选了其中一个答案,请直接写出他选中正确答案的概率是多少?
(2)如果其中有两个是正确的,某位同学随意选了其中两个答案,请用列举法或树状图求出他选中正确答案的概率是多少?
19.(本题满分5分)
已知:如图,点O在线段AC上,⊙O过B,C两点,交AC于点D,AB与⊙O相切,切点为B.
求证:∠ABD=∠C.
九年级数学试题(三年制)第4页(共8页)
20.(本题满分6分)
某商品原售价64元,经过连续两次降价后售价为36元,求平均每次降价的百分率为多少?
21.(本题满分6分)
如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC.
(1)求证: = ;
(2)求证:CD是⊙O的切线.
九年级数学试题(三年制)第5页(共8页)
22.(本题满分8分)
某商店购进一种商品,单价为30元.试销中发现这种商品每天的销售量P(件)与每件的销售价(元)的函数关系的图像如图所示.
(1)结合图像,直接写出每天的销售量P(件)与每件的销售价(元)的函数关系式.
(2)若商店在试销期间每天销售这种商品获得150元的利润,每件的销售价是多少元?
(3)如何定价能使每天的利润最大?
九年级数学试题(三年制)第6页(共8页)
23.(本题满分8分)
如图,在Rt△ABC中,∠C=90°.O,D分别为AB,BC上的点,经过A,D两点的⊙O分别交AB,AC于点E,F,且D为 的中点.
(1)求证:BC与⊙O相切;
(2)当AD=2,∠CAD=30°时,求 的长.
九年级数学试题(三年制)第7页(共8页)
24.(本题满分8分)
已知:抛物线,对称轴为直线,抛物线与y轴交于点,与轴交于、两点.
(1)求抛物线的解析式;
(2)直接写出直线的解析式;
(3)若点是线段下方抛物线上的动点,求四边形面积的最大值.
九年级数学试题(三年制)第8页(共8页)
2011—2012学年度第一学期期末考试
九年级数学试题(三年制)评分标准与参考答案
一、选择题
1.C 2.C 3.B 4.A 5.D 6.D 7.B 8.C 9.D 10.D
二、填空题
11.y=x2+1 12. 13.4 14.120 ° 15.10
三、解答题
16.解:原式=3×2-2×3+ …………………………………………… 1分
=6-6+ …………………………………………… 2分
= …………………………………………… 3分
17.(1)解:(x-5)2-2(x-5)=0
(x-5)(x-5-2)=0……………………………………… 1分
∴x-5=0或x-5-2=0……………………………………… 2分
∴x1=5,x2=7.……………………………………… 3分
(2)解: x2-4x=5
x2-4x+4=5+4
(x-2) 2=9………………………………………… 4分
x-2=±3…………………………………………5分
∴ x1=5,x2=-1.………………………………………… 6分
18.解:(1)选中正确答案的概率是.………………………………………… 2分
(2)列表法为:
第二个
D (A,D) (B,D) (C,D)
C (A,C) (B,C) (D,C)
B (A,B) (C,B) (D,B)
A (B,A) (C,A) (D,A)
A B C D 第一个
或树形图为:
可能出现的结果有12个,它们出现的可能性相等.
正确答案有两个,所以,P(选中正确答案)=. …………………… 5分
九年级数学试题(三年制)答案第1页(共4页)
19.证明:∵ CD是的直径,
∴ ∠1+∠2=90°.……………………… 1分
∵ AB是⊙O的切线,
∴ ∠1+∠ABD=90°.………………… 2分
∴ ∠ABD=∠2. ……………………… 3分
∵ OC=OB,
∴ ∠2=∠C. ……………………… 4分
∴ ∠ABD=∠C.……………………… 5分
20.解:设平均每次降价的百分率为x,由题意得:
64(1-x)2=36……………………………………………… 3分
解得:x1=25%,x2=175%(不合题意,舍去).……………………………… 5分
答:平均每次降价的百分率为25%.………………………………………………6分
21.证明:如图,连接OD. ………………… 1分
(1)∵ AD∥OC,
∴ ∠1=∠4, ∠2=∠3. ……………… 2分
又∵ OA=OD, ∴ ∠1=∠3.
∴ ∠3=∠4.
∴ = . …………………………… 3分
(2)在△COD和△COB中
∵ CO=CO,∠3=∠4,OD=OB,
∴ △COD≌△COB. … …………………… 4分
∴ ∠ODC=∠OBC=90°. ………………… 5分
∴ CD是⊙O的切线.……………………… 6分
22. (1)解:销售量P(件)与每件的销售价(元)的函数关系式为:
P=-2x+100. ……………………………………………2分
(2)解:由题意得:(-2x+100)(x-30)=150
解得:x1=35或x2=45.
答:要获得150元的利润,每件的销售价是35元或45元. ……………………………5分
(3)解:设每件的销售价(元),每天的利润为y元.
y=(-2x+100)(x-30)
=-2x2+160 x-3000
=-2(x-40) 2+200
∴每件的销售价为40元时,获得利润最大,最大利润是200元. ………………………8分
23.(1)证明:如图,连接OD,则OD=OA.
∴ ∠1=∠2.……………………………………… 1分
∵ = ,
∴ ∠1=∠3. ∴ ∠2=∠3.
∴ OD∥AC.……………………………………… 2分
九年级数学试题答案(四年制)第2页(共4页)
又∵ ∠C=90°, ∴ ∠ODC=90°.
即 BC⊥OD.……………………………… 3分
∴ BC与⊙O相切. ……………………… 4分
(2)解:连接DE,则 ∠ADE=90°.
∵ ∠1=∠2=∠3=30°,
∠4=120°. …………………………… 5分
在Rt△ADE中,设DE=x,则AE=2x.
∵x2+(2) 2=(2x) 2.…………………………… 6分
∴x=2.
∴AE=4.
∴ ⊙O的半径r=2.………………………………………………7分
∴ 求 的长 l==π.…………………………… 8分
24.解:(1)∵对称轴
∴ ……………………………………………………1分
∵
∴
∴抛物线的解析式为y=x2+2x-3.………………………2分
(2)直线AC的解析式为. ………………………………………4分
(3)代数方法一:
过点D作DM∥y轴分别交线段AC和x轴于点M、N.
设,则…………………………………5分
∵
……………………………………7分
∴当时,四边形ABCD面积有最大值. ………………………8分
九年级数学试题(三年制)答案第2页(共4页)
代数方法二:
=
= ……………………………………7分
∴当时,四边形ABCD面积有最大值.………………………8分
几何方法:
过点作的平行线,设直线的解析式为.
由得:………………………………5分
当时,直线与抛物线只有一个公共点
即:当时,△ADC的面积最大,四边形ABCD面积最大
此时公共点的坐标为 ………………………………6分
= ………………………………7分
即:当时,四边形ABCD面积有最大值.………………………………8分
九年级数学试题(三年制)答案第2页(共4页)
(第4题图)
(第5题图)
(第8题图)
(第9题图)
(第14题图)
(第15题图)
(第19题图)
(第21题图)
(第22题图)
(第23题图)
(第24题图)
(第18题解答图)
(第20题 第 (2) 题解答图)
(第22题解答图)
(第23题解答图)
(第23题解答图)
九年级数学试题(三年制)
题号 一 二 三 总分
16 17 18 19 20 21 22 23 24
得分
选择题答题栏
题 号 1 2 3 4 5 6 7 8 9 10
答 案
一、选择题(本大题满分30分,每小题3分.每小题只有一个符合题意的选项,请你将正确选项的代号填在答题栏内 )
1.-的值是
A.4 B. C.2 D.3
2.在等边三角形、正五边形、正六边形、正七边形中,既是轴对称图形,又是中心对称图形的是
A.等边三角形 B.正五边形 C.正六边形 D.正七边形
3.二次函数顶点坐标是
A.(-1,-2) B.(1,2) C.(-1,2) D.(0,2)
4.小红随意在如图所示的地板上踢键子,则键子恰落在黑色
方砖上的概率为
A. B. C. D.
5.如图,以O为圆心的两个同心圆中,大圆的弦是小圆的
切线.若大圆半径为,小圆半径为,则弦的长为
A.8cm B.10cm C.12cm D.16cm
6.用配方法将化成的形式为( ).
A. B.
C. D.
九年级数学试题(三年制)第1页(共8页)
7. 从甲、乙、丙、丁四人中用抽签的方式,选取二人打扫卫生,那么能同时选中甲、乙二人的概率为
A. B. C. D.
8.如图,P为⊙O外一点,PA,PB分别切⊙O于A、B,CD切
⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD
的周长为( )
A.5 B.8 C.10 D.12
9.如图,⊙O1、⊙O2相内切于点A,其半径分别是8和4,
将⊙O2沿直线O1 O2平移至两圆相外切时,则点O2移动的
长度是
A.4 B.8 C.16 D.8 或16
10.已知二次函数 y=ax2+bx+c的y与x的部分对应值如下表:
x … -1 0 1 2 …
y … -5 1 3 1 …
则下列判断中正确的是
A.该函数图象开口向上
B.该函数图象与y轴交于负半轴
C.方程ax2+bx+c=0的正根在1与2之间
D.方程ax2+bx+c=0的正根在2与3之间
二、填空题(本大题满分15分,每小题3分,请你将答案填写在题目中的横线上)
11.将抛物线y=x2的图象向上平移1个单位后,得到新的抛物线,则新的抛物线的解析式是 .
12.若正三角形的边长为6,则其内切圆的半径等于 .
13.在一个不透明的布袋中,有黄色、白色的乒乓球共10个,这些球除颜色外都相同.小刚通过多次摸球实验后发现其中摸到黄球的频率稳定在60%,则布袋中白球的个数很可能是 个.
14.如图,分别以A,B为圆心,线段AB的长为
半径的两个圆相交于C、D两点,则∠CAD的
度数为 .
九年级数学试题(三年制)第2页(共8页)
15.某中学生推铅球,铅球在点A处出手,在点B处落地,
它的运行路线如图所示满足y=-x2+ x+,则这个学生推
铅球的成绩是_____米.
三、解答题 (本大题满分55分, 解答要写出必要的文字说明或推演步骤)
16. (本题满分3分)
计算:
3-2+.
17.(本题满分6分,每小题3分)
解方程:
(1)(x-5)2=2(x-5)
(2)x2-4x-5=0
九年级数学试题(三年制)第3页(共8页)
18. (本题满分5分)
一道选择题共有A、B、C、D四个备选答案,
(1)如果其中只有一个是正确的,某位同学随意选了其中一个答案,请直接写出他选中正确答案的概率是多少?
(2)如果其中有两个是正确的,某位同学随意选了其中两个答案,请用列举法或树状图求出他选中正确答案的概率是多少?
19.(本题满分5分)
已知:如图,点O在线段AC上,⊙O过B,C两点,交AC于点D,AB与⊙O相切,切点为B.
求证:∠ABD=∠C.
九年级数学试题(三年制)第4页(共8页)
20.(本题满分6分)
某商品原售价64元,经过连续两次降价后售价为36元,求平均每次降价的百分率为多少?
21.(本题满分6分)
如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,弦AD∥OC.
(1)求证: = ;
(2)求证:CD是⊙O的切线.
九年级数学试题(三年制)第5页(共8页)
22.(本题满分8分)
某商店购进一种商品,单价为30元.试销中发现这种商品每天的销售量P(件)与每件的销售价(元)的函数关系的图像如图所示.
(1)结合图像,直接写出每天的销售量P(件)与每件的销售价(元)的函数关系式.
(2)若商店在试销期间每天销售这种商品获得150元的利润,每件的销售价是多少元?
(3)如何定价能使每天的利润最大?
九年级数学试题(三年制)第6页(共8页)
23.(本题满分8分)
如图,在Rt△ABC中,∠C=90°.O,D分别为AB,BC上的点,经过A,D两点的⊙O分别交AB,AC于点E,F,且D为 的中点.
(1)求证:BC与⊙O相切;
(2)当AD=2,∠CAD=30°时,求 的长.
九年级数学试题(三年制)第7页(共8页)
24.(本题满分8分)
已知:抛物线,对称轴为直线,抛物线与y轴交于点,与轴交于、两点.
(1)求抛物线的解析式;
(2)直接写出直线的解析式;
(3)若点是线段下方抛物线上的动点,求四边形面积的最大值.
九年级数学试题(三年制)第8页(共8页)
2011—2012学年度第一学期期末考试
九年级数学试题(三年制)评分标准与参考答案
一、选择题
1.C 2.C 3.B 4.A 5.D 6.D 7.B 8.C 9.D 10.D
二、填空题
11.y=x2+1 12. 13.4 14.120 ° 15.10
三、解答题
16.解:原式=3×2-2×3+ …………………………………………… 1分
=6-6+ …………………………………………… 2分
= …………………………………………… 3分
17.(1)解:(x-5)2-2(x-5)=0
(x-5)(x-5-2)=0……………………………………… 1分
∴x-5=0或x-5-2=0……………………………………… 2分
∴x1=5,x2=7.……………………………………… 3分
(2)解: x2-4x=5
x2-4x+4=5+4
(x-2) 2=9………………………………………… 4分
x-2=±3…………………………………………5分
∴ x1=5,x2=-1.………………………………………… 6分
18.解:(1)选中正确答案的概率是.………………………………………… 2分
(2)列表法为:
第二个
D (A,D) (B,D) (C,D)
C (A,C) (B,C) (D,C)
B (A,B) (C,B) (D,B)
A (B,A) (C,A) (D,A)
A B C D 第一个
或树形图为:
可能出现的结果有12个,它们出现的可能性相等.
正确答案有两个,所以,P(选中正确答案)=. …………………… 5分
九年级数学试题(三年制)答案第1页(共4页)
19.证明:∵ CD是的直径,
∴ ∠1+∠2=90°.……………………… 1分
∵ AB是⊙O的切线,
∴ ∠1+∠ABD=90°.………………… 2分
∴ ∠ABD=∠2. ……………………… 3分
∵ OC=OB,
∴ ∠2=∠C. ……………………… 4分
∴ ∠ABD=∠C.……………………… 5分
20.解:设平均每次降价的百分率为x,由题意得:
64(1-x)2=36……………………………………………… 3分
解得:x1=25%,x2=175%(不合题意,舍去).……………………………… 5分
答:平均每次降价的百分率为25%.………………………………………………6分
21.证明:如图,连接OD. ………………… 1分
(1)∵ AD∥OC,
∴ ∠1=∠4, ∠2=∠3. ……………… 2分
又∵ OA=OD, ∴ ∠1=∠3.
∴ ∠3=∠4.
∴ = . …………………………… 3分
(2)在△COD和△COB中
∵ CO=CO,∠3=∠4,OD=OB,
∴ △COD≌△COB. … …………………… 4分
∴ ∠ODC=∠OBC=90°. ………………… 5分
∴ CD是⊙O的切线.……………………… 6分
22. (1)解:销售量P(件)与每件的销售价(元)的函数关系式为:
P=-2x+100. ……………………………………………2分
(2)解:由题意得:(-2x+100)(x-30)=150
解得:x1=35或x2=45.
答:要获得150元的利润,每件的销售价是35元或45元. ……………………………5分
(3)解:设每件的销售价(元),每天的利润为y元.
y=(-2x+100)(x-30)
=-2x2+160 x-3000
=-2(x-40) 2+200
∴每件的销售价为40元时,获得利润最大,最大利润是200元. ………………………8分
23.(1)证明:如图,连接OD,则OD=OA.
∴ ∠1=∠2.……………………………………… 1分
∵ = ,
∴ ∠1=∠3. ∴ ∠2=∠3.
∴ OD∥AC.……………………………………… 2分
九年级数学试题答案(四年制)第2页(共4页)
又∵ ∠C=90°, ∴ ∠ODC=90°.
即 BC⊥OD.……………………………… 3分
∴ BC与⊙O相切. ……………………… 4分
(2)解:连接DE,则 ∠ADE=90°.
∵ ∠1=∠2=∠3=30°,
∠4=120°. …………………………… 5分
在Rt△ADE中,设DE=x,则AE=2x.
∵x2+(2) 2=(2x) 2.…………………………… 6分
∴x=2.
∴AE=4.
∴ ⊙O的半径r=2.………………………………………………7分
∴ 求 的长 l==π.…………………………… 8分
24.解:(1)∵对称轴
∴ ……………………………………………………1分
∵
∴
∴抛物线的解析式为y=x2+2x-3.………………………2分
(2)直线AC的解析式为. ………………………………………4分
(3)代数方法一:
过点D作DM∥y轴分别交线段AC和x轴于点M、N.
设,则…………………………………5分
∵
……………………………………7分
∴当时,四边形ABCD面积有最大值. ………………………8分
九年级数学试题(三年制)答案第2页(共4页)
代数方法二:
=
= ……………………………………7分
∴当时,四边形ABCD面积有最大值.………………………8分
几何方法:
过点作的平行线,设直线的解析式为.
由得:………………………………5分
当时,直线与抛物线只有一个公共点
即:当时,△ADC的面积最大,四边形ABCD面积最大
此时公共点的坐标为 ………………………………6分
= ………………………………7分
即:当时,四边形ABCD面积有最大值.………………………………8分
九年级数学试题(三年制)答案第2页(共4页)
(第4题图)
(第5题图)
(第8题图)
(第9题图)
(第14题图)
(第15题图)
(第19题图)
(第21题图)
(第22题图)
(第23题图)
(第24题图)
(第18题解答图)
(第20题 第 (2) 题解答图)
(第22题解答图)
(第23题解答图)
(第23题解答图)
同课章节目录
