2020-2021学年华东师大版九年级数学下册课件:27.4 正多边形和圆(20张)
文档属性
| 名称 | 2020-2021学年华东师大版九年级数学下册课件:27.4 正多边形和圆(20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 00:00:00 | ||
图片预览



文档简介
第27章 圆
27.4 正多边形和圆
博学 慎思
求真 至善
教学目标
教学重点与难点
重点:正多边形与圆的关系及其相关概念和应用.
难点:会用尺规画正多边形.
1.了解正多边形的定义及正多边形与圆的关系.
2.掌握正多边形的中心、半径、中心角、边心距的概念.
3.会应用正多边形的有关计算公式,熟记一些特殊正多边形的有关结论.
4.掌握用尺规画正n边形的方法.
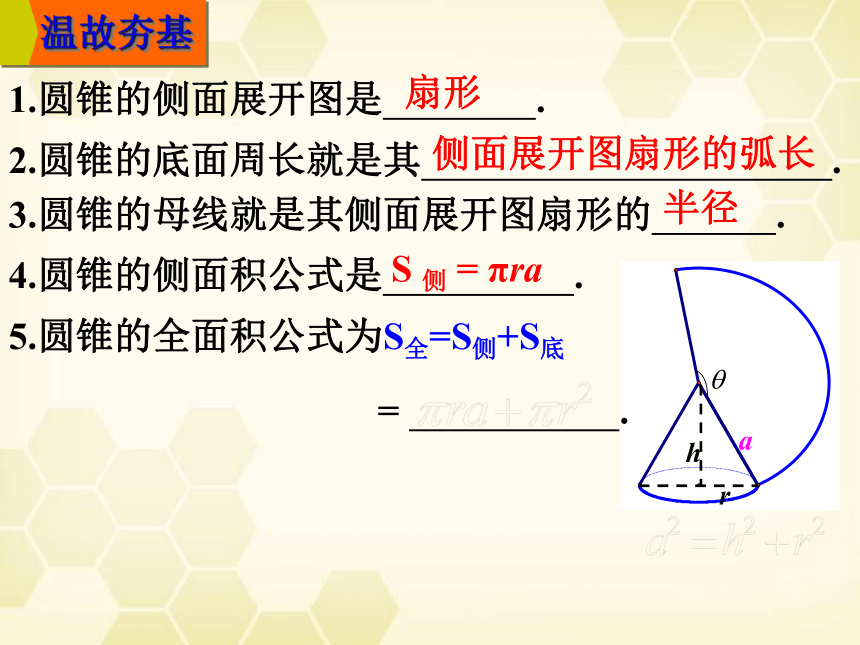
1.圆锥的侧面展开图是 .
2.圆锥的底面周长就是其 .
3.圆锥的母线就是其侧面展开图扇形的 .
a
h
r
4.圆锥的侧面积公式是 .
5.圆锥的全面积公式为S全=S侧+S底
温故夯基
扇形
侧面展开图扇形的弧长
半径
S 侧 = πra
= .
巩固练习
1.已知圆锥的高为4cm,母线长为5cm,则它的底面的周长
为 cm,侧面积为 cm2,全面积为 cm2.
2.已知圆锥形工件的底面直径是40cm,母线长30cm,
其侧面展开图的圆心角的度数为 .
240°
6π
15π
24π
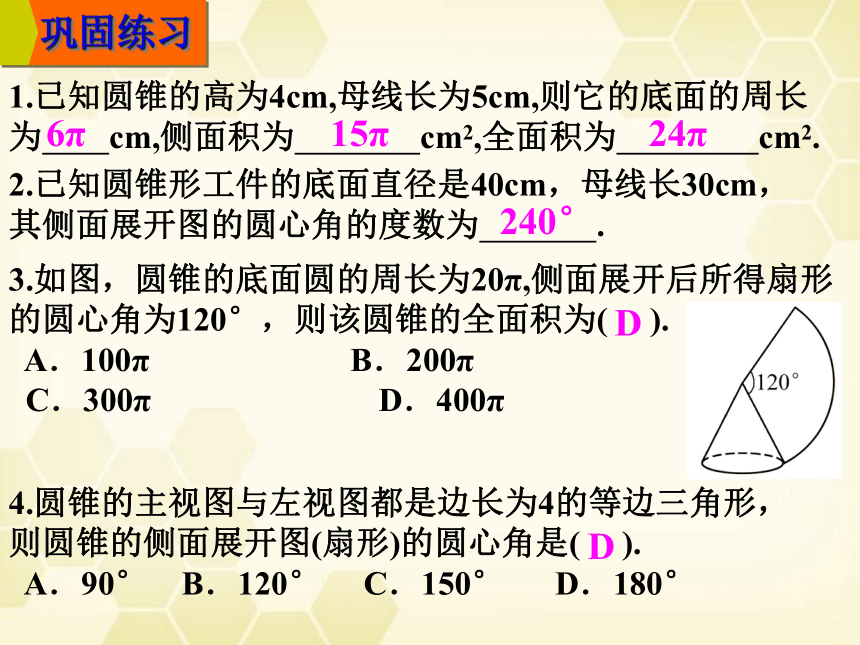
3.如图,圆锥的底面圆的周长为20π,侧面展开后所得扇形
的圆心角为120°,则该圆锥的全面积为( ).
A.100π B.200π
C.300π D.400π
4.圆锥的主视图与左视图都是边长为4的等边三角形,
则圆锥的侧面展开图(扇形)的圆心角是( ).
A.90° B.120° C.150° D.180°
D
D
知识回顾
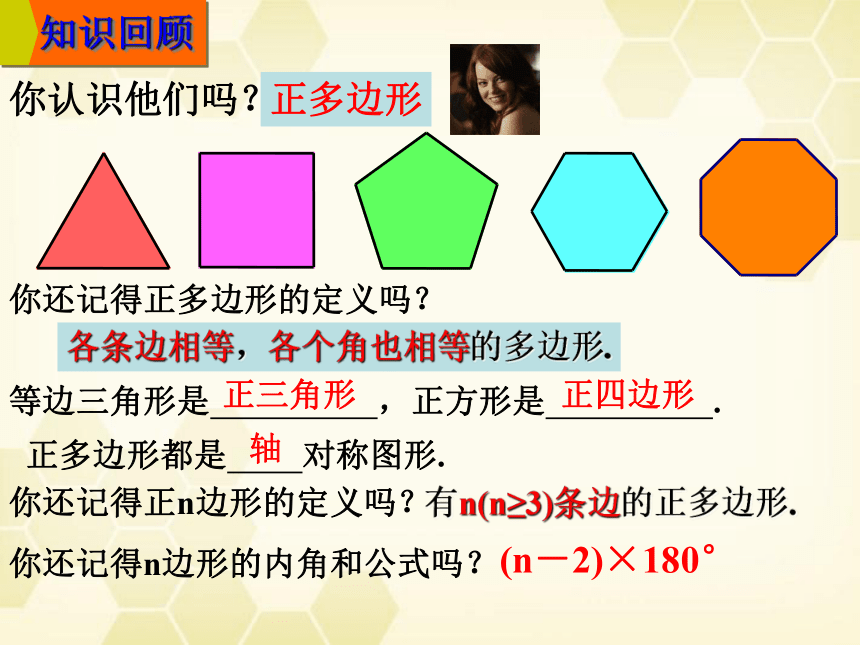
你认识他们吗?
正多边形
你还记得正多边形的定义吗?
各条边相等,各个角也相等的多边形.
等边三角形是 ,正方形是 .
正三角形
正四边形
正多边形都是 对称图形.
轴
你还记得正n边形的定义吗?
有n(n≥3)条边的正多边形.
你还记得n边形的内角和公式吗?
(n-2)×180°
学习新知
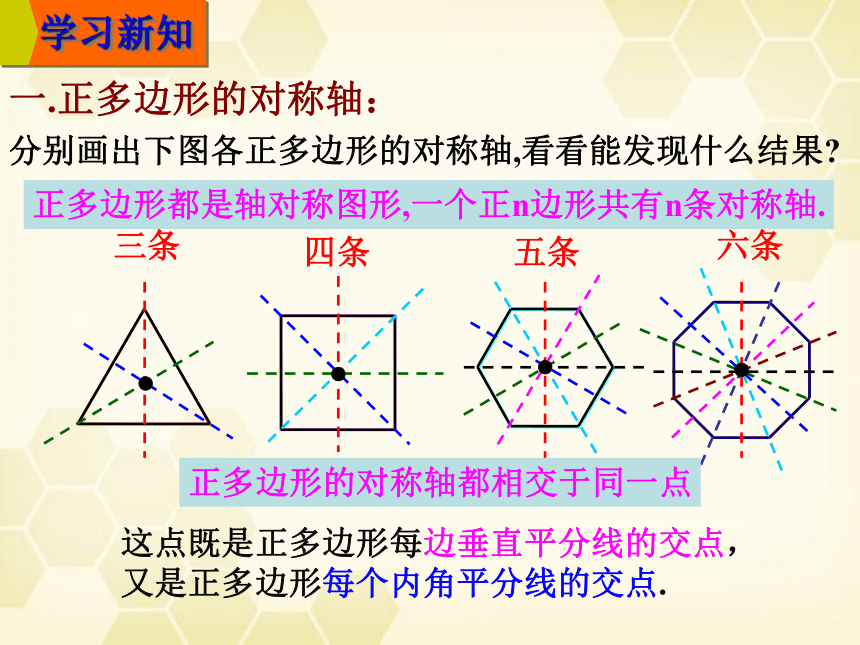
一.正多边形的对称轴:
分别画出下图各正多边形的对称轴,看看能发现什么结果?
三条
四条
五条
六条
正多边形都是轴对称图形,一个正n边形共有n条对称轴.
正多边形的对称轴都相交于同一点
这点既是正多边形每边垂直平分线的交点,
又是正多边形每个内角平分线的交点.
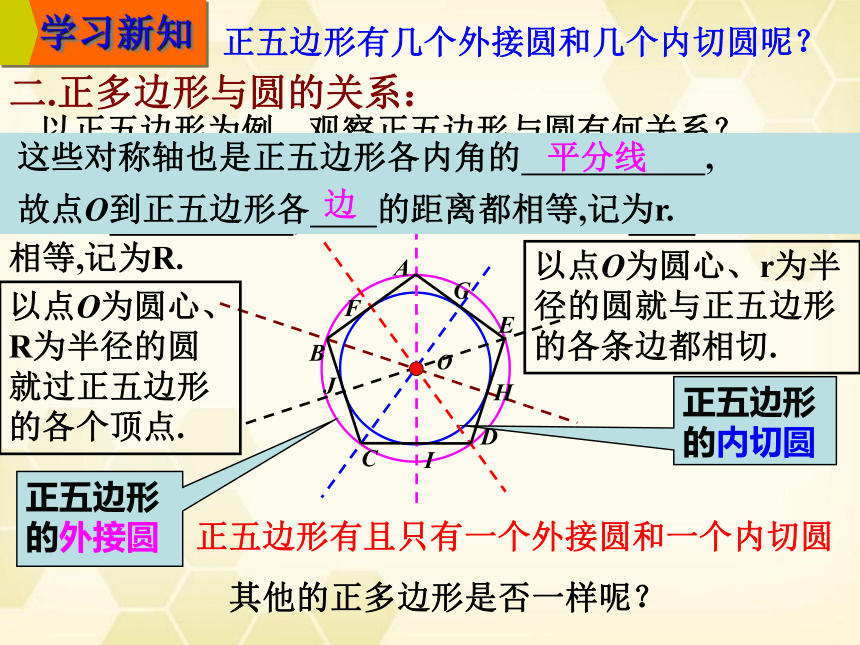
以正五边形为例,观察正五边形与圆有何关系?
A
B
C
D
E
O
F
J
I
H
G
正五边形
的内切圆
学习新知
二.正多边形与圆的关系:
正五边形的对称轴都交于一点O.这些对称轴是正五边形
各边的 ,故点O到正五边形各个 的距离
相等,记为R.
垂直平分线
顶点
以点O为圆心、
R为半径的圆
就过正五边形的各个顶点.
正五边形
的外接圆
这些对称轴也是正五边形各内角的 ,
故点O到正五边形各 的距离都相等,记为r.
平分线
边
以点O为圆心、r为半径的圆就与正五边形的各条边都相切.
正五边形有几个外接圆和几个内切圆呢?
正五边形有且只有一个外接圆和一个内切圆
其他的正多边形是否一样呢?
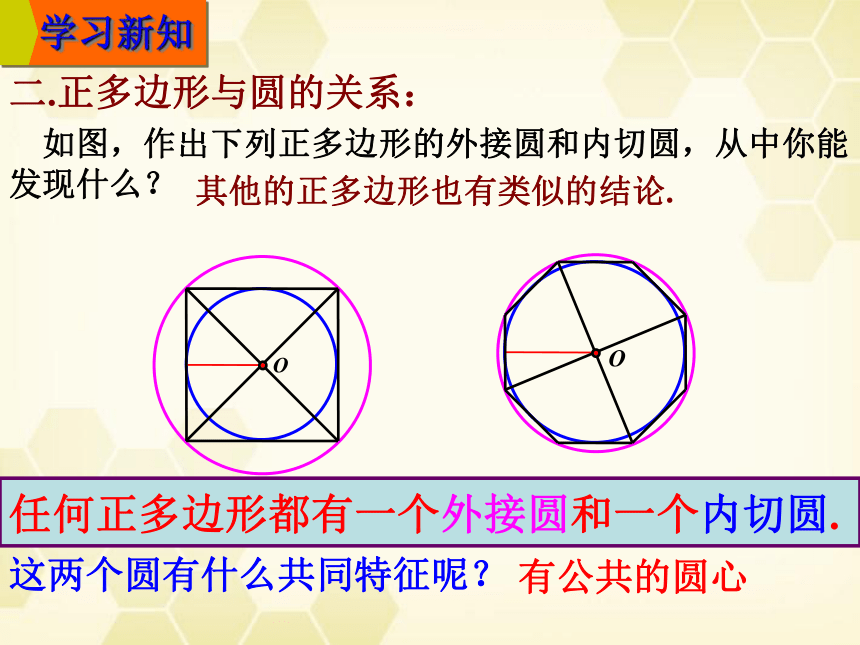
如图,作出下列正多边形的外接圆和内切圆,从中你能发现什么?
O
O
任何正多边形都有一个外接圆和一个内切圆.
学习新知
二.正多边形与圆的关系:
其他的正多边形也有类似的结论.
这两个圆有什么共同特征呢?
有公共的圆心
1.正多边形的中心:一个正多边形的外接圆(内切圆)的圆心叫做正多边形的中心.(即点O)
边心距r
2.正多边形的半径:正多边形外接圆的半径叫做正多边形的半径.(即点OA)
半径R
3.正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.(即∠AOB)
4.正多边形的边心距:中心到正多边形的一边的距离叫做正多边形的边心距.(内切圆的半径,即OM)
中心角
M
A
B
C
D
E
F
O
学习新知
三.正多边形的有关概念:
E
F
C
D
A
B
O
G
R
a
r
学习新知
四.正多边形的边长、半径、边心距和中心角之间
的关系:
若正多边形边数为n,边长为a,半径为R,边心距为r,
则有:
中心角为
周长L=na
即时应用
1.正六边形的中心角的度数是_____.
60°
2.正n边形的中心角为24°,则它的边数是_____.
15
3.正六边形外接圆的半径为6,则它的边心距是_____,
面积是_____.
4.若⊙O的半径R=4,则其内接正方形的边心距为_____.
E
F
C
D
A
B
O
G
6
a
r
A
B
C
D
E
4
·
A
B
C
D
E
O
A
B
C
D
E
为什么这样做的
就是正多边形呢?
学习新知
五.正多边形的画法:
作法:只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
在同圆或等圆中,如果弧相等,那么它们所对的弦相等.
作法:把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
例题精析
例 利用尺规作图,作出已知圆的内接正方形和内接
正六边形.
·
解:内接正方形的作法:
(1)用直尺任作圆的一条直径AC;
A
C
(2)作与直径AC垂直的直径BD;
B
D
(3)顺次连结所得的圆上四点,
则四边形ABCD即为所求作的正方形.
圆的内接正八边形怎么作?
过圆心作各边的垂线与⊙O相交,
或作各中心角的角平分线与⊙O相交,
即得圆接正八边形.
例题精析
例 利用尺规作图,作出已知圆的内接正方形和内接
正六边形.
·
内接正六边形的作法:
(1)用直尺任作圆的一条直径AD;
A
D
(2)以点A为圆心、OA为半径作圆,与⊙O交于点B、F;
O
B
F
(3)以点D为圆心、OD为半径作圆,与⊙O交于点C、E;
C
E
(4)顺次连结所得的圆上六点,
则六边形ABCDEF即为所求作
的正六边形.
O
F
A
B
D
E
·
C
例题精析
例 利用尺规作图,作出已知圆的内接正六边形.
.
如图,从圆上某一点开始,依次以圆的半径长为
半径作圆,也可以作出圆的内接正六边形.
想一想:为什么这两种方法作出来的图形都是正六边形?
因为这两种方法都是把圆
六等分,所以作出来的
图形都是正六边形.
圆的内接正三角形怎么作?
圆的内接正十二边形怎么作?
过圆心作各边的垂线与⊙O相交,
或作各中心角的角平分线与⊙O相交,
即得圆接正十二边形.
随堂练习
1.如图,正六边形ABCDEF内接于⊙O,则∠CFD的度数
是( ).
A. 60° B. 45° C. 30° D. 22.5°
C
D
E
F
A
B
O
C
2.如图,⊙O的半径R=6cm,则⊙O内接三角形ABC的边心距
为 ,边长为 ,周长为 ,面积为 .
A
B
C
O
第1题图
第2题图
D
6
3
3 cm
课堂小结
一.正多边形的对称轴:
正多边形都是轴对称图形,一个正n边形共有n条对称轴.
二.正多边形与圆的关系:
任何正多边形都有一个外接圆和一个内切圆.
三.正多边形的有关概念:
1.正多边形的中心:一个正多边形的外接圆(内切圆)的圆心.
2.正多边形的半径:正多边形外接圆的半径.
3.正多边形的中心角:正多边形每一边所对的圆心角.
4.正多边形的边心距:中心到正多边形的一边的距离.
(内切圆的半径)
E
F
C
D
A
B
O
G
R
a
r
四.正多边形的边长、半径、边心距和中心角之间
的关系:
若正多边形边数为n,边长为a,半径为R,边心距为r,
则有:
中心角为
周长L=na
课堂小结
作业与课外学习任务
1.作业:课本P67 习题27.4 2,3
练习:学习检测 P38-40 1~19
2.课外学习任务:
做好本章的复习工作!
教学反馈:
作业存在的主要问题:
27.4 正多边形和圆
博学 慎思
求真 至善
教学目标
教学重点与难点
重点:正多边形与圆的关系及其相关概念和应用.
难点:会用尺规画正多边形.
1.了解正多边形的定义及正多边形与圆的关系.
2.掌握正多边形的中心、半径、中心角、边心距的概念.
3.会应用正多边形的有关计算公式,熟记一些特殊正多边形的有关结论.
4.掌握用尺规画正n边形的方法.
1.圆锥的侧面展开图是 .
2.圆锥的底面周长就是其 .
3.圆锥的母线就是其侧面展开图扇形的 .
a
h
r
4.圆锥的侧面积公式是 .
5.圆锥的全面积公式为S全=S侧+S底
温故夯基
扇形
侧面展开图扇形的弧长
半径
S 侧 = πra
= .
巩固练习
1.已知圆锥的高为4cm,母线长为5cm,则它的底面的周长
为 cm,侧面积为 cm2,全面积为 cm2.
2.已知圆锥形工件的底面直径是40cm,母线长30cm,
其侧面展开图的圆心角的度数为 .
240°
6π
15π
24π
3.如图,圆锥的底面圆的周长为20π,侧面展开后所得扇形
的圆心角为120°,则该圆锥的全面积为( ).
A.100π B.200π
C.300π D.400π
4.圆锥的主视图与左视图都是边长为4的等边三角形,
则圆锥的侧面展开图(扇形)的圆心角是( ).
A.90° B.120° C.150° D.180°
D
D
知识回顾
你认识他们吗?
正多边形
你还记得正多边形的定义吗?
各条边相等,各个角也相等的多边形.
等边三角形是 ,正方形是 .
正三角形
正四边形
正多边形都是 对称图形.
轴
你还记得正n边形的定义吗?
有n(n≥3)条边的正多边形.
你还记得n边形的内角和公式吗?
(n-2)×180°
学习新知
一.正多边形的对称轴:
分别画出下图各正多边形的对称轴,看看能发现什么结果?
三条
四条
五条
六条
正多边形都是轴对称图形,一个正n边形共有n条对称轴.
正多边形的对称轴都相交于同一点
这点既是正多边形每边垂直平分线的交点,
又是正多边形每个内角平分线的交点.
以正五边形为例,观察正五边形与圆有何关系?
A
B
C
D
E
O
F
J
I
H
G
正五边形
的内切圆
学习新知
二.正多边形与圆的关系:
正五边形的对称轴都交于一点O.这些对称轴是正五边形
各边的 ,故点O到正五边形各个 的距离
相等,记为R.
垂直平分线
顶点
以点O为圆心、
R为半径的圆
就过正五边形的各个顶点.
正五边形
的外接圆
这些对称轴也是正五边形各内角的 ,
故点O到正五边形各 的距离都相等,记为r.
平分线
边
以点O为圆心、r为半径的圆就与正五边形的各条边都相切.
正五边形有几个外接圆和几个内切圆呢?
正五边形有且只有一个外接圆和一个内切圆
其他的正多边形是否一样呢?
如图,作出下列正多边形的外接圆和内切圆,从中你能发现什么?
O
O
任何正多边形都有一个外接圆和一个内切圆.
学习新知
二.正多边形与圆的关系:
其他的正多边形也有类似的结论.
这两个圆有什么共同特征呢?
有公共的圆心
1.正多边形的中心:一个正多边形的外接圆(内切圆)的圆心叫做正多边形的中心.(即点O)
边心距r
2.正多边形的半径:正多边形外接圆的半径叫做正多边形的半径.(即点OA)
半径R
3.正多边形的中心角:正多边形每一边所对的圆心角叫做正多边形的中心角.(即∠AOB)
4.正多边形的边心距:中心到正多边形的一边的距离叫做正多边形的边心距.(内切圆的半径,即OM)
中心角
M
A
B
C
D
E
F
O
学习新知
三.正多边形的有关概念:
E
F
C
D
A
B
O
G
R
a
r
学习新知
四.正多边形的边长、半径、边心距和中心角之间
的关系:
若正多边形边数为n,边长为a,半径为R,边心距为r,
则有:
中心角为
周长L=na
即时应用
1.正六边形的中心角的度数是_____.
60°
2.正n边形的中心角为24°,则它的边数是_____.
15
3.正六边形外接圆的半径为6,则它的边心距是_____,
面积是_____.
4.若⊙O的半径R=4,则其内接正方形的边心距为_____.
E
F
C
D
A
B
O
G
6
a
r
A
B
C
D
E
4
·
A
B
C
D
E
O
A
B
C
D
E
为什么这样做的
就是正多边形呢?
学习新知
五.正多边形的画法:
作法:只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
在同圆或等圆中,如果弧相等,那么它们所对的弦相等.
作法:把圆分成n(n>2)等份,依次连结各分点所得的多边形是这个圆的一个内接正n边形.
例题精析
例 利用尺规作图,作出已知圆的内接正方形和内接
正六边形.
·
解:内接正方形的作法:
(1)用直尺任作圆的一条直径AC;
A
C
(2)作与直径AC垂直的直径BD;
B
D
(3)顺次连结所得的圆上四点,
则四边形ABCD即为所求作的正方形.
圆的内接正八边形怎么作?
过圆心作各边的垂线与⊙O相交,
或作各中心角的角平分线与⊙O相交,
即得圆接正八边形.
例题精析
例 利用尺规作图,作出已知圆的内接正方形和内接
正六边形.
·
内接正六边形的作法:
(1)用直尺任作圆的一条直径AD;
A
D
(2)以点A为圆心、OA为半径作圆,与⊙O交于点B、F;
O
B
F
(3)以点D为圆心、OD为半径作圆,与⊙O交于点C、E;
C
E
(4)顺次连结所得的圆上六点,
则六边形ABCDEF即为所求作
的正六边形.
O
F
A
B
D
E
·
C
例题精析
例 利用尺规作图,作出已知圆的内接正六边形.
.
如图,从圆上某一点开始,依次以圆的半径长为
半径作圆,也可以作出圆的内接正六边形.
想一想:为什么这两种方法作出来的图形都是正六边形?
因为这两种方法都是把圆
六等分,所以作出来的
图形都是正六边形.
圆的内接正三角形怎么作?
圆的内接正十二边形怎么作?
过圆心作各边的垂线与⊙O相交,
或作各中心角的角平分线与⊙O相交,
即得圆接正十二边形.
随堂练习
1.如图,正六边形ABCDEF内接于⊙O,则∠CFD的度数
是( ).
A. 60° B. 45° C. 30° D. 22.5°
C
D
E
F
A
B
O
C
2.如图,⊙O的半径R=6cm,则⊙O内接三角形ABC的边心距
为 ,边长为 ,周长为 ,面积为 .
A
B
C
O
第1题图
第2题图
D
6
3
3 cm
课堂小结
一.正多边形的对称轴:
正多边形都是轴对称图形,一个正n边形共有n条对称轴.
二.正多边形与圆的关系:
任何正多边形都有一个外接圆和一个内切圆.
三.正多边形的有关概念:
1.正多边形的中心:一个正多边形的外接圆(内切圆)的圆心.
2.正多边形的半径:正多边形外接圆的半径.
3.正多边形的中心角:正多边形每一边所对的圆心角.
4.正多边形的边心距:中心到正多边形的一边的距离.
(内切圆的半径)
E
F
C
D
A
B
O
G
R
a
r
四.正多边形的边长、半径、边心距和中心角之间
的关系:
若正多边形边数为n,边长为a,半径为R,边心距为r,
则有:
中心角为
周长L=na
课堂小结
作业与课外学习任务
1.作业:课本P67 习题27.4 2,3
练习:学习检测 P38-40 1~19
2.课外学习任务:
做好本章的复习工作!
教学反馈:
作业存在的主要问题:
