人教版七年级数学下册5.1.3 同位角、内错角、同旁内角课件(共23张ppt)
文档属性
| 名称 | 人教版七年级数学下册5.1.3 同位角、内错角、同旁内角课件(共23张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 307.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 00:00:00 | ||
图片预览






文档简介
第五章 相交线与平行线
5.1 相交线
5.1.3 同位角、内错角、同旁内角
学习
目标
1.明确构成同位角、内错角、同旁内角的条件,了解其名称的含义.
2.经历在简单的图形中辨认同位角、内错角、同旁内角的过程,会在给定的某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
如图,直线a,b被直线l所截,一共形成8个角,根据同位角的定义:
互为同位角:_____________________________ _____________;
互为内错角:______________________;
互为同旁内角:______________________.
∠1与∠5,∠2与∠6,∠4与∠8,∠3与∠7
∠3与∠5,∠4与∠6
∠4与∠5,∠3与∠6
1.与同位角相比较,内错角也是由两条直线被第三条直线所截形成的角,你能说出内错角与同位角的主要异同点吗?
【答案】相同点:①都是两条直线被第三条直线所截形成的角;②都是根据两角的位置特征命名的角;③每对角都有一条公共边.
不同点:两对角的位置不同,同位角位于两条直线的同一方向且在截线的同旁,而内错角位于两条直线的内部且在截线的两旁.
2.与同位角相比较,同旁内角也是由两条直线被第三条直线所截形成的角,你能说出同旁内角与同位角的主要异同点吗?
【答案】相同点:①都是两条直线被第三条直线所截形成的角;②都是根据两角的位置特征命名的角;③每对角都有一条公共边.
不同点:两对角的位置不同,同位角位于两条直线的同一方向,而同旁内角位于两条直线之间.
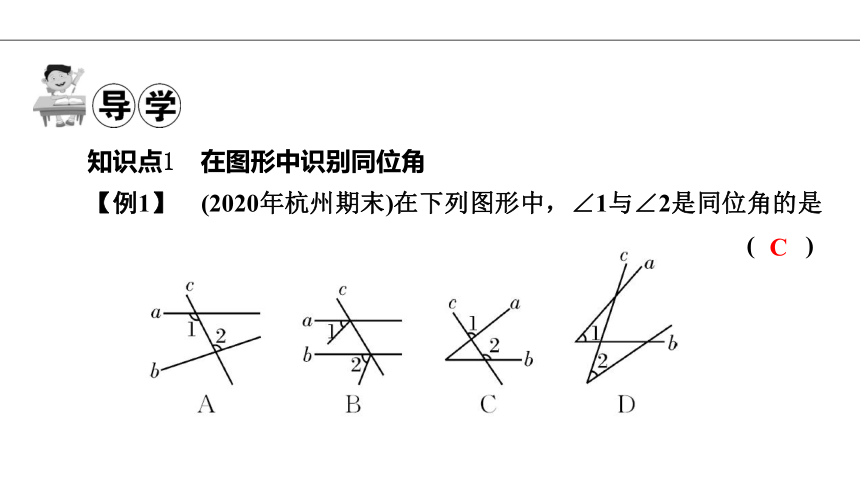
知识点1 在图形中识别同位角
【例1】 (2020年杭州期末)在下列图形中,∠1与∠2是同位角的是 ( )
C
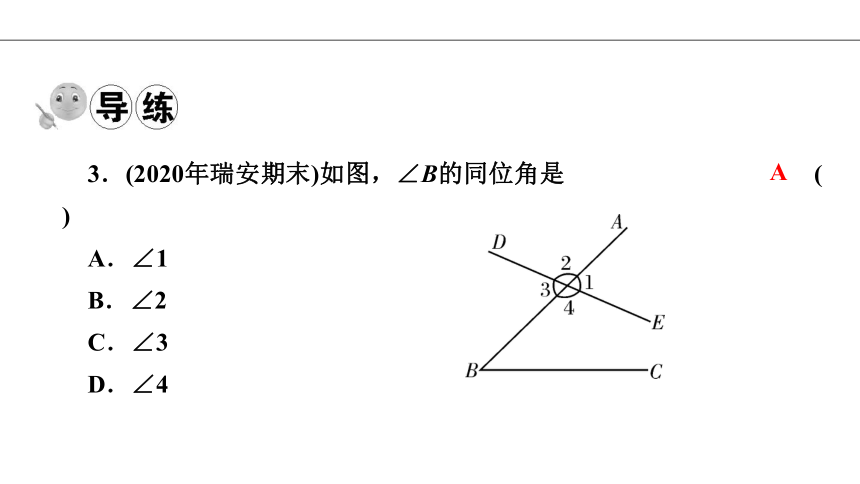
3.(2020年瑞安期末)如图,∠B的同位角是 ( )
A.∠1
B.∠2
C.∠3
D.∠4
A
方法点拨:在识别同位角时,要注意同位角的两个特点:从形成同位角的角度看,同位角一定有公共边,没有公共边的两个角一定不是同位角;从同位角的分布位置的角度看,同位角具有“同位”的特点,每对同位角都呈“F”型分布.
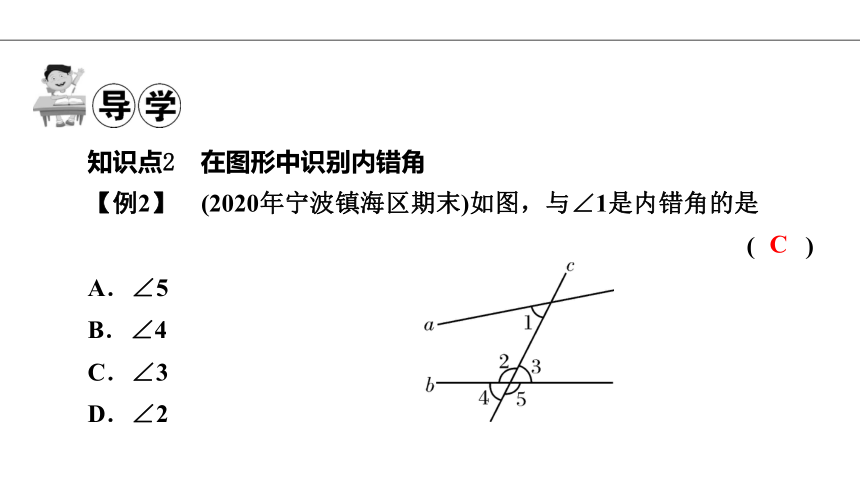
知识点2 在图形中识别内错角
【例2】 (2020年宁波镇海区期末)如图,与∠1是内错角的是
( )
A.∠5
B.∠4
C.∠3
D.∠2
C
4.如图的各角中,下列说法:①∠1与∠2是内错角;②∠2与∠3是同位角;③∠1与∠3是内错角;④∠2与∠4是内错角.其中正确的是 ( )
A.①②
B.③④
C.②③
D.①②③④
C
方法点拨:在识别内错角时,要注意内错角的两个特点:从形成内错角的角度看,内错角一定有公共边,没有公共边的两个角一定不是内错角;从内错角的分布位置的角度看,内错角具有“内”与“错”的特点,每对内错角都呈“Z”型分布.
知识点3 在图形中识别同旁内角
【例3】 (2020年温州期末)如图,下列选项中与∠A互为同旁内角的是 ( )
?
A.∠1 B.∠2
C.∠3 D.∠4
A
5.(2020年重庆沙坪坝区期末)如图,下列说法错误的是 ( )
A.∠1与∠3是对顶角
B.∠3与∠4是内错角
C.∠2与∠6是同位角
D.∠3与∠5是同旁内角
C
方法点拨:在识别同旁内角时,要注意同旁内角的两个特点:从形成同旁内角的角度看,同旁内角一定有公共边,没有公共边的两个角一定不是同旁内角;从同旁内角的分布位置的角度看,同旁内角具有“同旁”与“内”的特点,每对同旁内角都呈“U”型分布.
【第一关】 建议用时3分钟
1.(2020年嘉兴期末)如图,下列四个角中,与∠1构成一对同位角的是 ( )
A.∠2
B.∠3
C.∠4
D.∠5
B
2.(2020年沧州新华区期中)如图,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成 ( )
?
A.内错角 B.同位角
C.同旁内角 D.对顶角
A
3.如图,在△ABC中,∠B的同旁内角是______________.
∠A,∠C
【第二关】 建议用时6分钟
4.(2020年乐清市期末)如图,直线AB,CD被射线CE所截,与∠1构成同位角的是 ( )
A.∠2
B.∠3
C.∠4
D.∠5
D
5.(2020年北京顺义区期末)如图,与∠1是同旁内角的是_______;与∠2是内错角的是_______.
∠5
∠3
6.观察图形,回答问题:
(1)若直线ED,BC被直线AB所截,∠1的同位角是哪个角?
(2)若直线ED,BC被直线AF所截,∠3的内错角是哪个角?
(3)∠1和∠3是直线AB,AF被哪条直线所截构成的内错角?
(4)∠2和∠4是哪两条直线被直线BC所截构成的同位角?
解:(1)若直线ED,BC被直线AB所截,∠1的同位角是∠2.
(2)若直线ED,BC被直线AF所截,∠3的内错角是∠4.
(3)∠1和∠3是直线AB,AF被直线ED所截构成的内错角.
(4)∠2和∠4是直线AB,AF被直线BC所截构成的同位角.
【第三关】 自主选做
7.如图,射线AD,BE相交于点C,连接AB.
(1)图中有无与∠A是同位角的角?若有,是怎样形
成的?
(2)图中有无与∠A是内错角的角?若有,是怎样形成的?
(3)图中有无与∠A是同旁内角的角?若有,是怎样形成的?
【答案】(1)∠BCD;BE,AB被AD所截.
(2)∠ACE;BE,AB被AD所截.
(3)∠ACB;BE,AB被AD所截.
5.1 相交线
5.1.3 同位角、内错角、同旁内角
学习
目标
1.明确构成同位角、内错角、同旁内角的条件,了解其名称的含义.
2.经历在简单的图形中辨认同位角、内错角、同旁内角的过程,会在给定的某个条件下进行有关同位角、内错角、同旁内角的判定和计算.
如图,直线a,b被直线l所截,一共形成8个角,根据同位角的定义:
互为同位角:_____________________________ _____________;
互为内错角:______________________;
互为同旁内角:______________________.
∠1与∠5,∠2与∠6,∠4与∠8,∠3与∠7
∠3与∠5,∠4与∠6
∠4与∠5,∠3与∠6
1.与同位角相比较,内错角也是由两条直线被第三条直线所截形成的角,你能说出内错角与同位角的主要异同点吗?
【答案】相同点:①都是两条直线被第三条直线所截形成的角;②都是根据两角的位置特征命名的角;③每对角都有一条公共边.
不同点:两对角的位置不同,同位角位于两条直线的同一方向且在截线的同旁,而内错角位于两条直线的内部且在截线的两旁.
2.与同位角相比较,同旁内角也是由两条直线被第三条直线所截形成的角,你能说出同旁内角与同位角的主要异同点吗?
【答案】相同点:①都是两条直线被第三条直线所截形成的角;②都是根据两角的位置特征命名的角;③每对角都有一条公共边.
不同点:两对角的位置不同,同位角位于两条直线的同一方向,而同旁内角位于两条直线之间.
知识点1 在图形中识别同位角
【例1】 (2020年杭州期末)在下列图形中,∠1与∠2是同位角的是 ( )
C
3.(2020年瑞安期末)如图,∠B的同位角是 ( )
A.∠1
B.∠2
C.∠3
D.∠4
A
方法点拨:在识别同位角时,要注意同位角的两个特点:从形成同位角的角度看,同位角一定有公共边,没有公共边的两个角一定不是同位角;从同位角的分布位置的角度看,同位角具有“同位”的特点,每对同位角都呈“F”型分布.
知识点2 在图形中识别内错角
【例2】 (2020年宁波镇海区期末)如图,与∠1是内错角的是
( )
A.∠5
B.∠4
C.∠3
D.∠2
C
4.如图的各角中,下列说法:①∠1与∠2是内错角;②∠2与∠3是同位角;③∠1与∠3是内错角;④∠2与∠4是内错角.其中正确的是 ( )
A.①②
B.③④
C.②③
D.①②③④
C
方法点拨:在识别内错角时,要注意内错角的两个特点:从形成内错角的角度看,内错角一定有公共边,没有公共边的两个角一定不是内错角;从内错角的分布位置的角度看,内错角具有“内”与“错”的特点,每对内错角都呈“Z”型分布.
知识点3 在图形中识别同旁内角
【例3】 (2020年温州期末)如图,下列选项中与∠A互为同旁内角的是 ( )
?
A.∠1 B.∠2
C.∠3 D.∠4
A
5.(2020年重庆沙坪坝区期末)如图,下列说法错误的是 ( )
A.∠1与∠3是对顶角
B.∠3与∠4是内错角
C.∠2与∠6是同位角
D.∠3与∠5是同旁内角
C
方法点拨:在识别同旁内角时,要注意同旁内角的两个特点:从形成同旁内角的角度看,同旁内角一定有公共边,没有公共边的两个角一定不是同旁内角;从同旁内角的分布位置的角度看,同旁内角具有“同旁”与“内”的特点,每对同旁内角都呈“U”型分布.
【第一关】 建议用时3分钟
1.(2020年嘉兴期末)如图,下列四个角中,与∠1构成一对同位角的是 ( )
A.∠2
B.∠3
C.∠4
D.∠5
B
2.(2020年沧州新华区期中)如图,两只手的食指和拇指在同一平面内,它们构成的一对角可以看成 ( )
?
A.内错角 B.同位角
C.同旁内角 D.对顶角
A
3.如图,在△ABC中,∠B的同旁内角是______________.
∠A,∠C
【第二关】 建议用时6分钟
4.(2020年乐清市期末)如图,直线AB,CD被射线CE所截,与∠1构成同位角的是 ( )
A.∠2
B.∠3
C.∠4
D.∠5
D
5.(2020年北京顺义区期末)如图,与∠1是同旁内角的是_______;与∠2是内错角的是_______.
∠5
∠3
6.观察图形,回答问题:
(1)若直线ED,BC被直线AB所截,∠1的同位角是哪个角?
(2)若直线ED,BC被直线AF所截,∠3的内错角是哪个角?
(3)∠1和∠3是直线AB,AF被哪条直线所截构成的内错角?
(4)∠2和∠4是哪两条直线被直线BC所截构成的同位角?
解:(1)若直线ED,BC被直线AB所截,∠1的同位角是∠2.
(2)若直线ED,BC被直线AF所截,∠3的内错角是∠4.
(3)∠1和∠3是直线AB,AF被直线ED所截构成的内错角.
(4)∠2和∠4是直线AB,AF被直线BC所截构成的同位角.
【第三关】 自主选做
7.如图,射线AD,BE相交于点C,连接AB.
(1)图中有无与∠A是同位角的角?若有,是怎样形
成的?
(2)图中有无与∠A是内错角的角?若有,是怎样形成的?
(3)图中有无与∠A是同旁内角的角?若有,是怎样形成的?
【答案】(1)∠BCD;BE,AB被AD所截.
(2)∠ACE;BE,AB被AD所截.
(3)∠ACB;BE,AB被AD所截.
