上海市闵行区2011学年第一学期高三年级质量调研考试数学(文理科)试卷及答案
文档属性
| 名称 | 上海市闵行区2011学年第一学期高三年级质量调研考试数学(文理科)试卷及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 264.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-09 11:22:57 | ||
图片预览




文档简介
闵行区2011学年第一学期高三年级质量调研考试
数 学 试 卷(文理科)
考生注意:
1.答卷前,考生务必在答题纸上将学校、姓名及准考证号等填写清楚,并在规定的区域内贴上条形码.答题时客观题用2B铅笔按要求涂写,主观题用黑色水笔填写.
2.本试卷共有23道题,共4页.满分150分,考试时间120分钟.
3.考试后只交答题纸,试卷由考生自己保留.
一. 填空题(本大题满分56分)本大题共有14题,考生应在答题纸上相应编号的空格
内直接填写结果,每个空格填对得4分,否则一律得零分.
1.若,,,
则 .
2.已知扇形的面积为,半径为1,则该扇形的圆心角的弧度数是 .
3.已知,命题“若,则”的否命题是 .
4.若为第二象限角,且,则的值为 .
5.椭圆上一焦点与短轴两端点形成的三角形的面积为1,则 .
6.设向量满足,,且与的方向相反,则的坐标为 .
7.已知直线与两点,若直线与线段相交,则的取值范围是 .
8.若,则对于, .
9.在中,若,且,则的大小为 .
10.执行右图所示的程序框图,若输入,则输出的值为 .
11.(文)已知数列{}的前项和,则 .
(理)设等差数列的首项及公差均是正整数,前项和为,且,,,则= .
12.(文) 若函数满足,且当时,,则函数的零点个数为 个.
(理)若偶函数满足,且当时,,则函数的零点个数为 个.
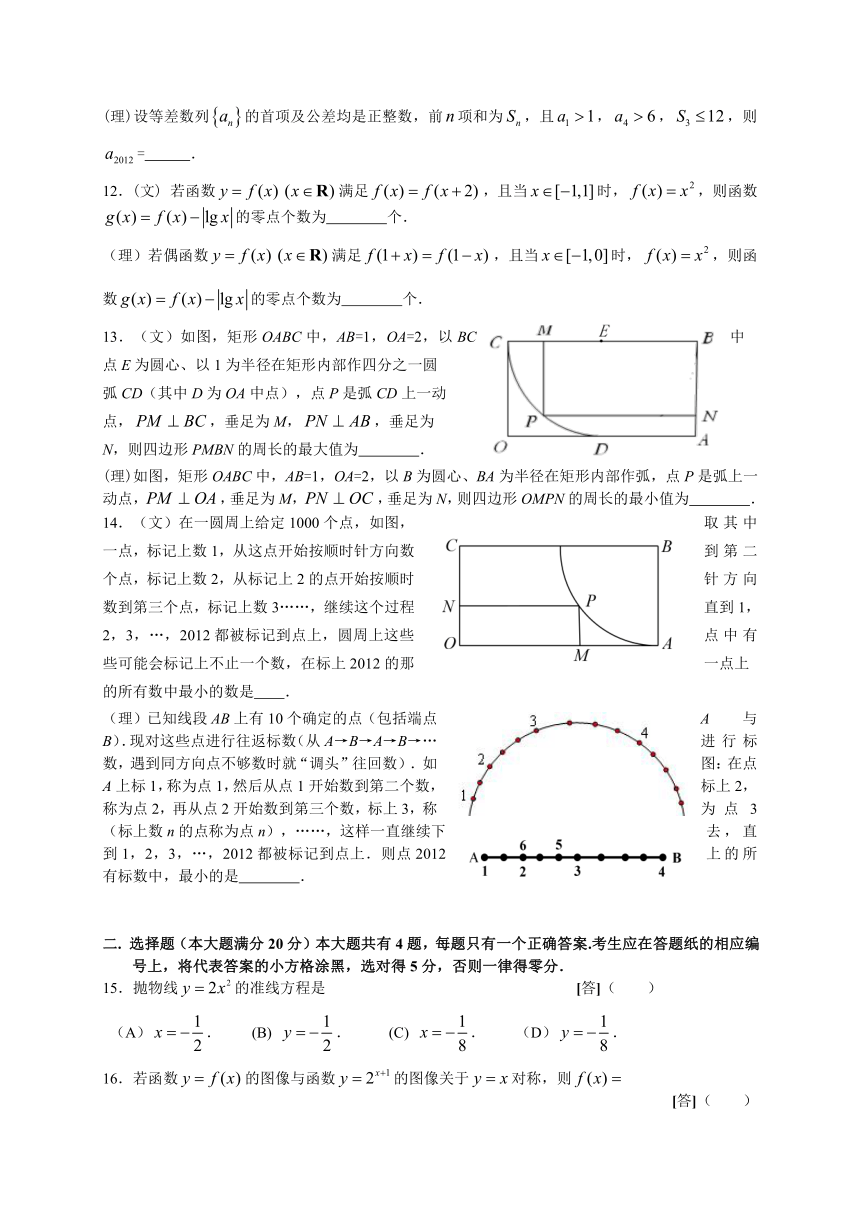
13.(文)如图,矩形OABC中,AB=1,OA=2,以BC中
点E为圆心、以1为半径在矩形内部作四分之一圆
弧CD(其中D为OA中点),点P是弧CD上一动
点,,垂足为M,,垂足为
N,则四边形PMBN的周长的最大值为 .
(理)如图,矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,,垂足为M,,垂足为N,则四边形OMPN的周长的最小值为 .
14.(文)在一圆周上给定1000个点,如图,取其中一点,标记上数1,从这点开始按顺时针方向数到第二个点,标记上数2,从标记上2的点开始按顺时针方向数到第三个点,标记上数3……,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标上2012的那一点上
的所有数中最小的数是 .
(理)已知线段AB上有10个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1,称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),……,这样一直继续下去,直到1,2,3,…,2012都被标记到点上.则点2012上的所有标数中,最小的是 .
二. 选择题(本大题满分20分)本大题共有4题,每题只有一个正确答案.考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.抛物线的准线方程是 [答]( )
(A). (B) . (C) . (D).
16.若函数的图像与函数的图像关于对称,则
[答]( )
(A) . (B) . (C) . (D) .
17.已知关于的二元一次线性方程组的增广矩阵为,记,则此线性方程组有无穷多组解的充要条件是
[答]( )
(A) . (B) 两两平行.
(C) . (D) 方向都相同.
18.(文)设、是关于的方程的两个不相等的实数根,那么过两点,的直线与圆的位置关系是 [答]( )
(A)相离. (B)相切. (C)相交. (D)随的变化而变化.
(理)设、是关于的方程的两个不相等的实数根,那么过两点,的直线与圆的位置关系是 [答]( )
(A)相离. (B)相切. (C)相交. (D)随的变化而变化.
三. 解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)
对于,规定向量的“*”运算为:.
若.解不等式.
20.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
(文)设双曲线的虚轴长为,渐近线方程是,为坐标原点,直线与双曲线相交于、两点,且.
(1)求双曲线的方程;
(2)求点的轨迹方程.
(理)设双曲线,是它实轴的两个端点,是其虚轴的一个端点.已知其渐近线的方向向量是,的面积是,为坐标原点,直线与双曲线C相交于、两点,且.
(1)求双曲线的方程;
(2)求点的轨迹方程.
21.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共层,总开发费用为万元,求函数的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
22.(本题满分16分)本题共有3个小题,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分7分.
(文)将边长分别为1、2、3、…、n、n+1、…()的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8,设前n个阴影部分图形的周长的平均值为,记数列满足.
(1)求的表达式;
(2)写出的值,并求数列的通项公式;
(3)记,若不等式有解,求的取值范围.
(理)将边长分别为1、2、3、4、…、n、n+1、…()的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为.记数列满足,.
(1)求的表达式;
(2)写出的值,并求数列的通项公式;
(3)记,若不等式有解,求的取值范围.
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)记函数在区间D上的最大值与最小值分别为与.
设函数(),,
令,记.
(1)若函数在上单调递减,求的取值范围;
(2)当时,求关于的表达式;
(3)试写出的表达式,并求.
(理)记函数在区间D上的最大值与最小值分别为与.
设函数,.,
(1)若函数在上单调递减,求的取值范围;
(2)若.令.记.试写出的表达式,并求.
(3)令(其中I为的定义域).若I恰好为,求b的取值范围,并求.
闵行区2011学年第一学期高三年级质量调研考试
数学试卷参考答案与评分标准
一. 填空题 1.; 2.; 3.若,则;
4.; 5.; 6.;
7.; 8.; 9.;
10.23; 11.(文)、(理) 4024; 12.10;
13.(文)、(理); 14.(文)12、(理)3.
二. 选择题 15. D;16.C;17.B;18.(文)B、(理)D
三. 解答题19.(本题满分12分)
解: (8分)
. (12分)
20.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
解:(1)(文)由题意,有,, (4分)
故双曲线的方程为. (6分)
(理)由题意,双曲线的渐近线方程为,则有
又的面积是,故 ,得 (4分)
所以双曲线的方程为. (6分)
(2)设,直线:与双曲线联立消去,
得 (8分)由题意,
且又由知(10分)而
所以,(12分)化简得①
由可得② 由①②可得
故点P的轨迹方程是 (14分)
21.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
(1)由已知,每幢经适楼房最下面一层的总建筑费用为:
(元)(万元),
从第二层开始,每幢每层的建筑总费用比其下面一层多:
(元)(万元),
每幢楼房从下到上各层的总建筑费用构成以75为首项,2 为公差的等差数列,(2分)
所以函数表达式为:
; (6分)
(2)由(1)知经适楼房每平方米平均开发费用为:
(10分)
(元) (12分)
当且仅当,即时等号成立,
但由于,验算:当时,,当时,.
答:该经适楼建为13层时,每平方米平均开发费用最低. (14分)
22.(本题满分16分)本题共有3个小题,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分7分.
解:(文)(1)第n个阴影部分图形的周长为8n, (2分)
故. (4分)
(2),, (7分)
当n为奇数时,
当n为偶数时,
故. (9分)
(3)
有解有解,
当n为奇数时,即
,
亦即有解,故 (12分)
当n为偶数时,
即,
于是,故. (14分)
综上所述:. (16分)
(理)解:(1)由题意,第1个阴影部分图形的面积为,第2个阴影部分图形的面积为,……,第n个阴影部分图形的面积为.(2分)
故
(4分)
(2),,, (7分)
当n为偶数时,,
当n为大于1的奇数时,,
故. (9分)
(3)由(2)知.
又.
(ⅰ)当n=1时,即,于是
(ⅱ)当n为偶数时,
即
于是,. (12分)
(ⅲ)当n为大于1的奇数时,
即
于是,. (14分)
综上所述:. (16分)
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
解:(文)(1) (2分)
由题意. (4分)
(2)当时,,,
显然g(x)在上单调递减,在上单调递增,又此时
故, (6分)
(8分)
从而:=. (10分)
(3).
1)当时,=g(1)=a+2b-1, =g(3)=3a+b
此时,.
2) 当时,=g(3)=3a+b, = g(1)=a+2b-1
此时,. (12分)
3) 当时,= g(1)=a+2b-1,= g(b)=ab+b, 此时,.
4) 当时,=g(3)=3a+b,= g(b)=ab+b, 此时,.
故, (14分)
因在上单调递减,在单调递增,故=h()=, (16分)
故当时,得. (18分)
(理)(1),(2分)由题意.(4分)
(2) .
(ⅰ)当时,= g(1)=a+2b-1,
= g(b)=ab+b, 此时,.
(ⅱ)当时,=g(3)=3a+b,
= g(b)=ab+b, 此时,.
故, (6分)
因在上单调递减,在单调递增,故=h()=, (8分)
故当时,得. (10分)
(3)(ⅰ)当时,f(x)=b,
(ⅱ)当,即时,
(ⅲ)当时,即(*), (13分)
①若2b-3>1即b>2, 由(*)知,但此时,所以b>2不合题意.
②若2b-3即b2, 由(*)知,
此时, 故, (15分)
且,于是,
当时,
当时,
即 (17分)
从而可得当a=0时,=0. (18分)
开始
输入x
是
否
结束
y=2x+1
输出y
数 学 试 卷(文理科)
考生注意:
1.答卷前,考生务必在答题纸上将学校、姓名及准考证号等填写清楚,并在规定的区域内贴上条形码.答题时客观题用2B铅笔按要求涂写,主观题用黑色水笔填写.
2.本试卷共有23道题,共4页.满分150分,考试时间120分钟.
3.考试后只交答题纸,试卷由考生自己保留.
一. 填空题(本大题满分56分)本大题共有14题,考生应在答题纸上相应编号的空格
内直接填写结果,每个空格填对得4分,否则一律得零分.
1.若,,,
则 .
2.已知扇形的面积为,半径为1,则该扇形的圆心角的弧度数是 .
3.已知,命题“若,则”的否命题是 .
4.若为第二象限角,且,则的值为 .
5.椭圆上一焦点与短轴两端点形成的三角形的面积为1,则 .
6.设向量满足,,且与的方向相反,则的坐标为 .
7.已知直线与两点,若直线与线段相交,则的取值范围是 .
8.若,则对于, .
9.在中,若,且,则的大小为 .
10.执行右图所示的程序框图,若输入,则输出的值为 .
11.(文)已知数列{}的前项和,则 .
(理)设等差数列的首项及公差均是正整数,前项和为,且,,,则= .
12.(文) 若函数满足,且当时,,则函数的零点个数为 个.
(理)若偶函数满足,且当时,,则函数的零点个数为 个.
13.(文)如图,矩形OABC中,AB=1,OA=2,以BC中
点E为圆心、以1为半径在矩形内部作四分之一圆
弧CD(其中D为OA中点),点P是弧CD上一动
点,,垂足为M,,垂足为
N,则四边形PMBN的周长的最大值为 .
(理)如图,矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,,垂足为M,,垂足为N,则四边形OMPN的周长的最小值为 .
14.(文)在一圆周上给定1000个点,如图,取其中一点,标记上数1,从这点开始按顺时针方向数到第二个点,标记上数2,从标记上2的点开始按顺时针方向数到第三个点,标记上数3……,继续这个过程直到1,2,3,…,2012都被标记到点上,圆周上这些点中有些可能会标记上不止一个数,在标上2012的那一点上
的所有数中最小的数是 .
(理)已知线段AB上有10个确定的点(包括端点A与B).现对这些点进行往返标数(从A→B→A→B→…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点A上标1,称为点1,然后从点1开始数到第二个数,标上2,称为点2,再从点2开始数到第三个数,标上3,称为点3(标上数n的点称为点n),……,这样一直继续下去,直到1,2,3,…,2012都被标记到点上.则点2012上的所有标数中,最小的是 .
二. 选择题(本大题满分20分)本大题共有4题,每题只有一个正确答案.考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.
15.抛物线的准线方程是 [答]( )
(A). (B) . (C) . (D).
16.若函数的图像与函数的图像关于对称,则
[答]( )
(A) . (B) . (C) . (D) .
17.已知关于的二元一次线性方程组的增广矩阵为,记,则此线性方程组有无穷多组解的充要条件是
[答]( )
(A) . (B) 两两平行.
(C) . (D) 方向都相同.
18.(文)设、是关于的方程的两个不相等的实数根,那么过两点,的直线与圆的位置关系是 [答]( )
(A)相离. (B)相切. (C)相交. (D)随的变化而变化.
(理)设、是关于的方程的两个不相等的实数根,那么过两点,的直线与圆的位置关系是 [答]( )
(A)相离. (B)相切. (C)相交. (D)随的变化而变化.
三. 解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)
对于,规定向量的“*”运算为:.
若.解不等式.
20.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
(文)设双曲线的虚轴长为,渐近线方程是,为坐标原点,直线与双曲线相交于、两点,且.
(1)求双曲线的方程;
(2)求点的轨迹方程.
(理)设双曲线,是它实轴的两个端点,是其虚轴的一个端点.已知其渐近线的方向向量是,的面积是,为坐标原点,直线与双曲线C相交于、两点,且.
(1)求双曲线的方程;
(2)求点的轨迹方程.
21.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共层,总开发费用为万元,求函数的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
22.(本题满分16分)本题共有3个小题,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分7分.
(文)将边长分别为1、2、3、…、n、n+1、…()的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.容易知道第1个阴影部分图形的周长为8,设前n个阴影部分图形的周长的平均值为,记数列满足.
(1)求的表达式;
(2)写出的值,并求数列的通项公式;
(3)记,若不等式有解,求的取值范围.
(理)将边长分别为1、2、3、4、…、n、n+1、…()的正方形叠放在一起,形成如图所示的图形.由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第n个阴影部分图形.设前n个阴影部分图形的面积的平均值为.记数列满足,.
(1)求的表达式;
(2)写出的值,并求数列的通项公式;
(3)记,若不等式有解,求的取值范围.
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(文)记函数在区间D上的最大值与最小值分别为与.
设函数(),,
令,记.
(1)若函数在上单调递减,求的取值范围;
(2)当时,求关于的表达式;
(3)试写出的表达式,并求.
(理)记函数在区间D上的最大值与最小值分别为与.
设函数,.,
(1)若函数在上单调递减,求的取值范围;
(2)若.令.记.试写出的表达式,并求.
(3)令(其中I为的定义域).若I恰好为,求b的取值范围,并求.
闵行区2011学年第一学期高三年级质量调研考试
数学试卷参考答案与评分标准
一. 填空题 1.; 2.; 3.若,则;
4.; 5.; 6.;
7.; 8.; 9.;
10.23; 11.(文)、(理) 4024; 12.10;
13.(文)、(理); 14.(文)12、(理)3.
二. 选择题 15. D;16.C;17.B;18.(文)B、(理)D
三. 解答题19.(本题满分12分)
解: (8分)
. (12分)
20.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
解:(1)(文)由题意,有,, (4分)
故双曲线的方程为. (6分)
(理)由题意,双曲线的渐近线方程为,则有
又的面积是,故 ,得 (4分)
所以双曲线的方程为. (6分)
(2)设,直线:与双曲线联立消去,
得 (8分)由题意,
且又由知(10分)而
所以,(12分)化简得①
由可得② 由①②可得
故点P的轨迹方程是 (14分)
21.(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
(1)由已知,每幢经适楼房最下面一层的总建筑费用为:
(元)(万元),
从第二层开始,每幢每层的建筑总费用比其下面一层多:
(元)(万元),
每幢楼房从下到上各层的总建筑费用构成以75为首项,2 为公差的等差数列,(2分)
所以函数表达式为:
; (6分)
(2)由(1)知经适楼房每平方米平均开发费用为:
(10分)
(元) (12分)
当且仅当,即时等号成立,
但由于,验算:当时,,当时,.
答:该经适楼建为13层时,每平方米平均开发费用最低. (14分)
22.(本题满分16分)本题共有3个小题,第(1)小题满分4分,第(2)小题满分5分,第(3)小题满分7分.
解:(文)(1)第n个阴影部分图形的周长为8n, (2分)
故. (4分)
(2),, (7分)
当n为奇数时,
当n为偶数时,
故. (9分)
(3)
有解有解,
当n为奇数时,即
,
亦即有解,故 (12分)
当n为偶数时,
即,
于是,故. (14分)
综上所述:. (16分)
(理)解:(1)由题意,第1个阴影部分图形的面积为,第2个阴影部分图形的面积为,……,第n个阴影部分图形的面积为.(2分)
故
(4分)
(2),,, (7分)
当n为偶数时,,
当n为大于1的奇数时,,
故. (9分)
(3)由(2)知.
又.
(ⅰ)当n=1时,即,于是
(ⅱ)当n为偶数时,
即
于是,. (12分)
(ⅲ)当n为大于1的奇数时,
即
于是,. (14分)
综上所述:. (16分)
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
解:(文)(1) (2分)
由题意. (4分)
(2)当时,,,
显然g(x)在上单调递减,在上单调递增,又此时
故, (6分)
(8分)
从而:=. (10分)
(3).
1)当时,=g(1)=a+2b-1, =g(3)=3a+b
此时,.
2) 当时,=g(3)=3a+b, = g(1)=a+2b-1
此时,. (12分)
3) 当时,= g(1)=a+2b-1,= g(b)=ab+b, 此时,.
4) 当时,=g(3)=3a+b,= g(b)=ab+b, 此时,.
故, (14分)
因在上单调递减,在单调递增,故=h()=, (16分)
故当时,得. (18分)
(理)(1),(2分)由题意.(4分)
(2) .
(ⅰ)当时,= g(1)=a+2b-1,
= g(b)=ab+b, 此时,.
(ⅱ)当时,=g(3)=3a+b,
= g(b)=ab+b, 此时,.
故, (6分)
因在上单调递减,在单调递增,故=h()=, (8分)
故当时,得. (10分)
(3)(ⅰ)当时,f(x)=b,
(ⅱ)当,即时,
(ⅲ)当时,即(*), (13分)
①若2b-3>1即b>2, 由(*)知,但此时,所以b>2不合题意.
②若2b-3即b2, 由(*)知,
此时, 故, (15分)
且,于是,
当时,
当时,
即 (17分)
从而可得当a=0时,=0. (18分)
开始
输入x
是
否
结束
y=2x+1
输出y
同课章节目录
