人教版六年级数学下册 4 比例 练习八(31页PPT)
文档属性
| 名称 | 人教版六年级数学下册 4 比例 练习八(31页PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览











文档简介
比例
4
1 比例的意义和基本性质
练习八
复习回顾
2.4:1.6=60:40
像这样表示两个比相等的式子叫做比例。
1
比例的意义
2
比例的基本性质
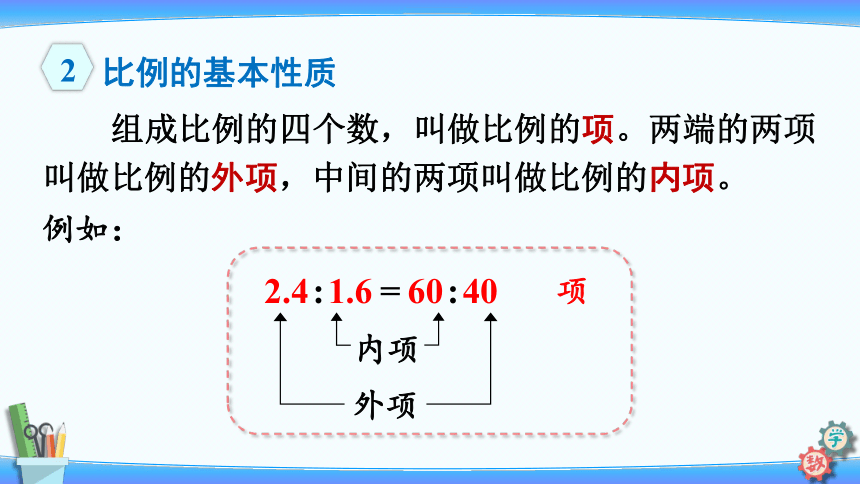
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
例如:
2.4:1.6=60:40
外项
内项
项
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
或
2.4:1.6=60:40
外项
内项
外项
内项
2
比例的基本性质
3
解比例
解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项的过程叫做解比例。
强化巩固
(教科书第43页练习八)
1. 下面各表中相对应的两个量的比能否组成比例?
如果能,把组成的比例写出来。
不能
能,2:30=8:120
年龄/岁
12
14
身高/m
1.4
1.6
箱子数量/个
2
8
质 量/kg
30
120
不能
能,5:100=10:200
时间/时
2
3
路程/km
30
40
衣服数量/件
5
10
总 价/元
100
200
2. 哪组中的四个数可以组成比例?把组成的比例写
出来。
(1)4,5,12和15
(2)2,3,4和5
(3)1.6,6.4,2和5
不能组成比例
4:5=12:15
不能组成比例
(答案不唯一)
(答案不唯一)
3. 写出比值是5的两个比,并组成比例。
(答案不唯一)
例:5:1 10:2 5:1=10:2
4. 李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8
公顷。秋收时,两块水稻田的产量分别为3.75t和6t。
(1)两块水稻田的产量与面积之比,是否可以组成比例?
因为3.75×0.8=3,0.5×6=3,所以产量与面积之比可以组成比例。
3.75:0.5=6:0.8或6:0.8=3.75:0.5
4. 李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8
公顷。秋收时,两块水稻田的产量分别为3.75t和6t。
(2)如果可以组成比例,指出比例的内项和外项。
3.75:0.5=6:0.8,3.75和0.8是外项,0.5和6是内项。6:0.8=3.75:0.5,6和0.5是外项,0.8和3.75是内项。
5. 应用比例的基本性质,判断下面哪组中的两个比可
以组成比例。
(2)1.4:2和28:40
(1)6:9和9:12
不能组成比例
6×12=72
9×9=81
6×12≠9×9
能组成比例
1.4×40=56
2×28=56
1.4×40=2×28
1.4:2和28:40
5. 应用比例的基本性质,判断下面哪组中的两个比可
以组成比例。
(4)7.5:1.3和5.7:3.1
能组成比例
不能组成比例
7.5×3.1=23.25
1.3×5.7=7.41
1.4×40≠1.3×5.7
小红说的对吗?
6.
7. 已知24×3=8×9,根据比例的基本性质,你能写
出比例吗?你能写几个?
24:8=9:3 24:9=8:3
3:8=9:24 3:9=8:24
8:24=3:9 9:24=3:8
8:3=24:9 9:3=24:8
能写8个
8. 解比例。
(2)0.8:4=x:8
4x=0.8×8
x=1.6
8. 解比例。
x =3
2x=8×9
x=36
9. 相同质量的水和冰的体积之比是9:10。一块体积
是50dm3的冰,化成水后的体积是多少?
解:设化成水后的体积是xdm3。
答:化成水后的体积是45dm3。
x:50=9:10
10x=50×9
x=45
10. 按照下面的条件列出比例,并且解比例。
(1)5和8的比等于40与x的比。
5:8=40:x
x=64
10. 按照下面的条件列出比例,并且解比例。
(3)比例的两个内项分别是2和5,两个外项分别是x和2.5。
x:2=5:2.5
2.5x=2×5
x=4
11. 汽车厂按1:20的比生产了一批汽车模型。
(1)轿车模型长24.3cm,轿车的实际长度是多少?
解:设轿车的实际长度是xcm。
答:轿车的实际长度是486cm。
24.3:x=1:20
x=20×24.3
x=486
11. 汽车厂按1:20的比生产了一批汽车模型。
(2)公共汽车长11.76m,模型车的长度是多少?
解:设模型车的长度是xcm。
答:模型车的长度是0.588m。
x:11.76=1:20
20x=11.76×1
x=0.588
12. 博物馆展出了一个高为19.6cm的秦代将军俑模型,
它的高度与实际高度的比是1:10。这个将军俑的
实际高度是多少?
解:设这个将军俑的实际高度是xcm。
答:这个将军俑的实际高度是196cm。
19.6:x=1:10
x=19.6×10
x=196
13. 育新小区1号楼的实际高度为35m,它的高度与
模型高度的比是500:1。模型的高度是多少厘米?
解:设模型的高度是xcm。
500:1=3500:x
x=7
答:模型的高度是7cm。
14. 把下面的等式改写成比例。
(1)3×40=8×15
(2)2.5×0.4=0.5×2
3:8=15:40
2.5:0.5=2:0.4
3:15=8:40
40:8=15:3
40:15=8:3
8:3=40:15
15:3=40:8
8:40=3:15
15:40=3:8
2.5:2=0.5:0.4
0.4:0.5=2:2.5
0.4:2=0.5:2.5
0.5:2.5=0.4:2
0.5:0.4=2.5:2
2:2.5=0.4:0.5
2:0.4=2.5:0.5
15. 李老师买了6个足球和8个篮球,买两种球所花钱
数相等。
(1)足球与篮球的单价之比是多少?
(2)足球的单价是40元,篮球的单价是多少?
4:3
解:设篮球的单价是x元。
40:x=4:3
x=30
答:篮球的单价是30元。
15. 李老师买了6个足球和8个篮球,买两种球所花钱
数相等。
(3)你还能提出其他数学问题并解答吗?
(答案不唯一)
例:篮球的单价是36元,足球的单价是多少元?
解:设足球的单价是y元。
y:36=8:6
y=48
答:足球的单价是48元。
判定两个比能否组成比例,一是要观察两个比的比值是否相等,二是在比例里两个外项的积是否等于两个内项的积。
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
4
1 比例的意义和基本性质
练习八
复习回顾
2.4:1.6=60:40
像这样表示两个比相等的式子叫做比例。
1
比例的意义
2
比例的基本性质
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
例如:
2.4:1.6=60:40
外项
内项
项
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质。
或
2.4:1.6=60:40
外项
内项
外项
内项
2
比例的基本性质
3
解比例
解比例根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的另外一个未知项。求比例中的未知项的过程叫做解比例。
强化巩固
(教科书第43页练习八)
1. 下面各表中相对应的两个量的比能否组成比例?
如果能,把组成的比例写出来。
不能
能,2:30=8:120
年龄/岁
12
14
身高/m
1.4
1.6
箱子数量/个
2
8
质 量/kg
30
120
不能
能,5:100=10:200
时间/时
2
3
路程/km
30
40
衣服数量/件
5
10
总 价/元
100
200
2. 哪组中的四个数可以组成比例?把组成的比例写
出来。
(1)4,5,12和15
(2)2,3,4和5
(3)1.6,6.4,2和5
不能组成比例
4:5=12:15
不能组成比例
(答案不唯一)
(答案不唯一)
3. 写出比值是5的两个比,并组成比例。
(答案不唯一)
例:5:1 10:2 5:1=10:2
4. 李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8
公顷。秋收时,两块水稻田的产量分别为3.75t和6t。
(1)两块水稻田的产量与面积之比,是否可以组成比例?
因为3.75×0.8=3,0.5×6=3,所以产量与面积之比可以组成比例。
3.75:0.5=6:0.8或6:0.8=3.75:0.5
4. 李叔叔承包了两块水稻田,面积分别为0.5公顷和0.8
公顷。秋收时,两块水稻田的产量分别为3.75t和6t。
(2)如果可以组成比例,指出比例的内项和外项。
3.75:0.5=6:0.8,3.75和0.8是外项,0.5和6是内项。6:0.8=3.75:0.5,6和0.5是外项,0.8和3.75是内项。
5. 应用比例的基本性质,判断下面哪组中的两个比可
以组成比例。
(2)1.4:2和28:40
(1)6:9和9:12
不能组成比例
6×12=72
9×9=81
6×12≠9×9
能组成比例
1.4×40=56
2×28=56
1.4×40=2×28
1.4:2和28:40
5. 应用比例的基本性质,判断下面哪组中的两个比可
以组成比例。
(4)7.5:1.3和5.7:3.1
能组成比例
不能组成比例
7.5×3.1=23.25
1.3×5.7=7.41
1.4×40≠1.3×5.7
小红说的对吗?
6.
7. 已知24×3=8×9,根据比例的基本性质,你能写
出比例吗?你能写几个?
24:8=9:3 24:9=8:3
3:8=9:24 3:9=8:24
8:24=3:9 9:24=3:8
8:3=24:9 9:3=24:8
能写8个
8. 解比例。
(2)0.8:4=x:8
4x=0.8×8
x=1.6
8. 解比例。
x =3
2x=8×9
x=36
9. 相同质量的水和冰的体积之比是9:10。一块体积
是50dm3的冰,化成水后的体积是多少?
解:设化成水后的体积是xdm3。
答:化成水后的体积是45dm3。
x:50=9:10
10x=50×9
x=45
10. 按照下面的条件列出比例,并且解比例。
(1)5和8的比等于40与x的比。
5:8=40:x
x=64
10. 按照下面的条件列出比例,并且解比例。
(3)比例的两个内项分别是2和5,两个外项分别是x和2.5。
x:2=5:2.5
2.5x=2×5
x=4
11. 汽车厂按1:20的比生产了一批汽车模型。
(1)轿车模型长24.3cm,轿车的实际长度是多少?
解:设轿车的实际长度是xcm。
答:轿车的实际长度是486cm。
24.3:x=1:20
x=20×24.3
x=486
11. 汽车厂按1:20的比生产了一批汽车模型。
(2)公共汽车长11.76m,模型车的长度是多少?
解:设模型车的长度是xcm。
答:模型车的长度是0.588m。
x:11.76=1:20
20x=11.76×1
x=0.588
12. 博物馆展出了一个高为19.6cm的秦代将军俑模型,
它的高度与实际高度的比是1:10。这个将军俑的
实际高度是多少?
解:设这个将军俑的实际高度是xcm。
答:这个将军俑的实际高度是196cm。
19.6:x=1:10
x=19.6×10
x=196
13. 育新小区1号楼的实际高度为35m,它的高度与
模型高度的比是500:1。模型的高度是多少厘米?
解:设模型的高度是xcm。
500:1=3500:x
x=7
答:模型的高度是7cm。
14. 把下面的等式改写成比例。
(1)3×40=8×15
(2)2.5×0.4=0.5×2
3:8=15:40
2.5:0.5=2:0.4
3:15=8:40
40:8=15:3
40:15=8:3
8:3=40:15
15:3=40:8
8:40=3:15
15:40=3:8
2.5:2=0.5:0.4
0.4:0.5=2:2.5
0.4:2=0.5:2.5
0.5:2.5=0.4:2
0.5:0.4=2.5:2
2:2.5=0.4:0.5
2:0.4=2.5:0.5
15. 李老师买了6个足球和8个篮球,买两种球所花钱
数相等。
(1)足球与篮球的单价之比是多少?
(2)足球的单价是40元,篮球的单价是多少?
4:3
解:设篮球的单价是x元。
40:x=4:3
x=30
答:篮球的单价是30元。
15. 李老师买了6个足球和8个篮球,买两种球所花钱
数相等。
(3)你还能提出其他数学问题并解答吗?
(答案不唯一)
例:篮球的单价是36元,足球的单价是多少元?
解:设足球的单价是y元。
y:36=8:6
y=48
答:足球的单价是48元。
判定两个比能否组成比例,一是要观察两个比的比值是否相等,二是在比例里两个外项的积是否等于两个内项的积。
课堂小结
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
