人教版六年级数学下册6 整理与复习 数与代数第5课时 式与方程(共21张ppt)
文档属性
| 名称 | 人教版六年级数学下册6 整理与复习 数与代数第5课时 式与方程(共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 00:00:00 | ||
图片预览





文档简介
整理和复习
1 数与代数
6
第5课时 式与方程
情境导入
我们知道,用字母表示
数可以简明地表达数量、数
量关系、运算定律和计算公
式等,为研究和解决问题带
来很多方便。
新课探究
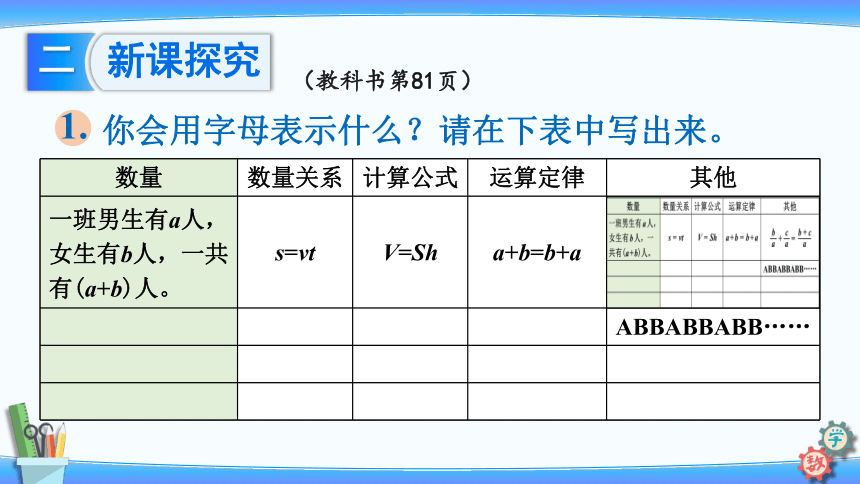
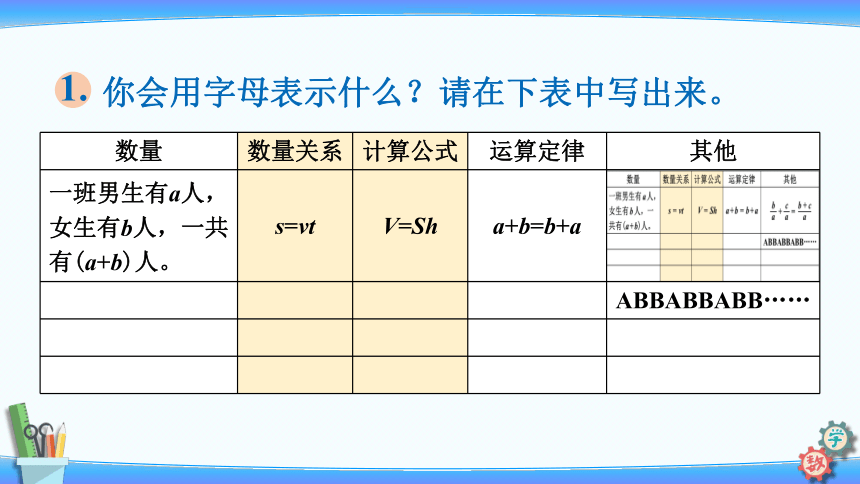
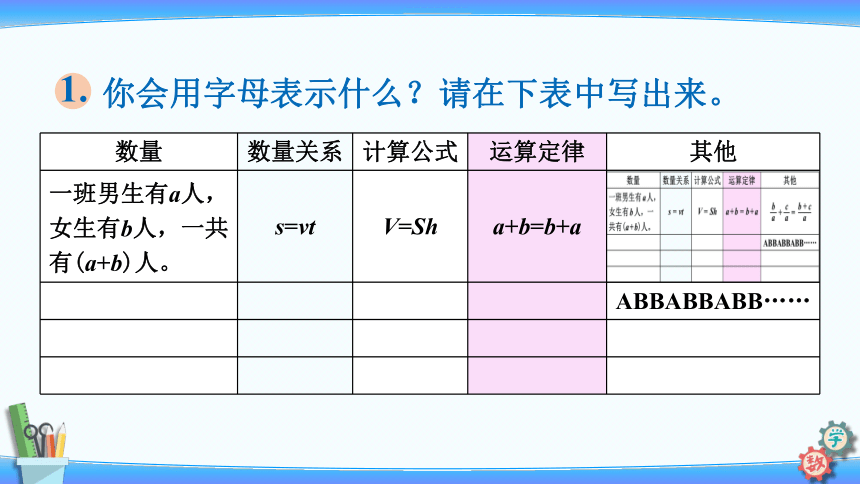
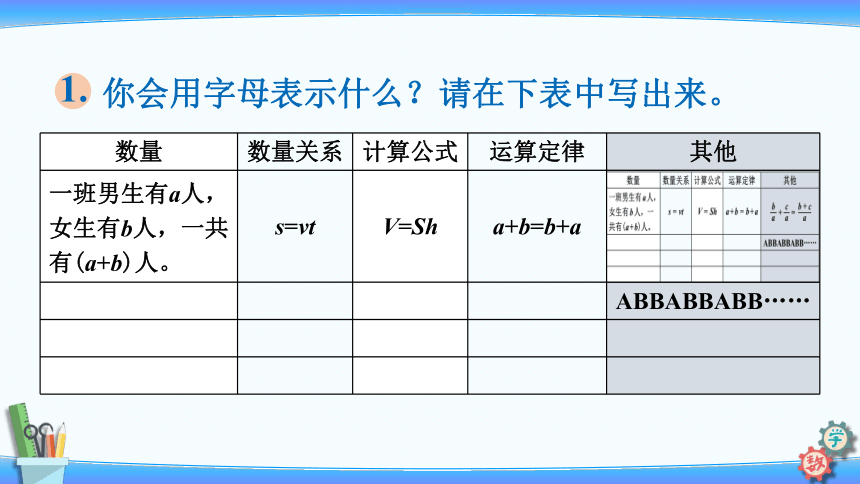
你会用字母表示什么?请在下表中写出来。
1.
(教科书第81页)
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
一、
用字母表示数量。
用字母或含有字母的式子可以表示数量,也可
以表示数量关系、运算定律和计算公式等,为研究
和解决问题带来很多方便。如:
一班成绩优秀的有x人,良好的有y人,及格的有z人。
一班喜欢音乐的有m人,喜欢舞蹈的有n人。
……
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
你会用字母表示什么?请在下表中写出来。
1.
二、
用字母表示数量关系。
总价=单价×数量
c=an
工作量=效率×时间
c=at
三、
用字母表示计算公式。
圆环的面积=大圆的面积?小圆的面积
S圆环=S大圆?S小圆
长方形的面积=长×宽
S=ab
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
你会用字母表示什么?请在下表中写出来。
1.
四、
用字母表示运算定律。
名称
用字母表示
加法交换律
a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=ac+bc
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
你会用字母表示什么?请在下表中写出来。
1.
五、
用字母表示计算方法。
用字母表示除法、分数或比时,表示除数、分母以及
比的后项的字母不能是0。
用字母表示运算结果时,必须是最简明的式子。
想一想,在一个含有字母的式子里,数与字母、
字母与字母相乘,书写时应注意什么?
2.
字母与字母、字母与数字之间的乘号可以记
作“·”或省略不写。但要注意,在省略乘号的
时候,应当把数字写在字母的前面。
如:
a·b
3x
方程与等式有什么区别和联系?
3.
为了求未知数,利用某种数量关系在已知数与未知数
之间建立的等式关系就是方程。
表示相等关系的式子叫作等式。
(1)
方程必须是等式,等式不一定是方程。
(2)
方程必须含有未知数,等式可以不含有未知数。
等式
方程
你能举例说明等式的性质吗?
4.
(1)
等式两边加上或减去同一个数,左右两边仍
然相等。如:
(2)
等式两边乘同一个数,或除以同一个不为0的
数,左右两边仍然相等。如:
3×4=2×6
3×4+4=2×6+4
3×4=2×6
3×4×4=2×6×4
3×4÷4=2×6÷4
用方程解决实际问
题,有什么特点?
(1)
弄清题意,找出未知
数,并用字母x表示
(也可以间接设某个量为x,再通过这个量去
求未知数)。
(2)
分析实际问题中的数量关系,找出等量关系,并
列出方程。
(3)
解方程,求出未知数的值。
(4)
检验方程的解是否符合题意,并写出答语。
随堂练习
(教科书第81页上方做一做)
1.
连线。
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a3
3a
a+3
a?3
2.
(教科书第81页下方做一做)
解:设小云踢了x下。
x=56
答:小云踢了56下。
培优训练
一个学生在爬山中,上山、下山共用了4小时。如
果她上山用了2.4小时,原路返回时下山的速度是
15千米/时,求她上山的速度。
1.
解:设她上山的速度为xkm/h。
2.4x=(4?2.4)×15
2.4x=24
x=10
答:她上山的速度是10km/h。
2.
甲、乙两车都从A城开往B城,甲车每小时行80
千米,乙车每小时行60千米。乙车先行驶2小时
后,甲车才开始出发,多少小时后甲车追上乙车?
解:设x小时后甲车追上乙车。
(80?60)x=2×60
20x=120
x=6
答:6小时后甲车追上乙车。
3.
用一根绳子测井深,将绳4折,井外还余8尺;将绳
6折,正好等于井深,绳长几尺?井深几尺?
解:设井深x尺,则绳长6x尺。
6x=4x+8
2x=8
x=4
答:绳长24尺,井深4尺。
6x=24
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
1 数与代数
6
第5课时 式与方程
情境导入
我们知道,用字母表示
数可以简明地表达数量、数
量关系、运算定律和计算公
式等,为研究和解决问题带
来很多方便。
新课探究
你会用字母表示什么?请在下表中写出来。
1.
(教科书第81页)
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
一、
用字母表示数量。
用字母或含有字母的式子可以表示数量,也可
以表示数量关系、运算定律和计算公式等,为研究
和解决问题带来很多方便。如:
一班成绩优秀的有x人,良好的有y人,及格的有z人。
一班喜欢音乐的有m人,喜欢舞蹈的有n人。
……
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
你会用字母表示什么?请在下表中写出来。
1.
二、
用字母表示数量关系。
总价=单价×数量
c=an
工作量=效率×时间
c=at
三、
用字母表示计算公式。
圆环的面积=大圆的面积?小圆的面积
S圆环=S大圆?S小圆
长方形的面积=长×宽
S=ab
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
你会用字母表示什么?请在下表中写出来。
1.
四、
用字母表示运算定律。
名称
用字母表示
加法交换律
a+b=b+a
加法结合律
乘法交换律
乘法结合律
乘法分配律
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=ac+bc
数量
数量关系
计算公式
运算定律
其他
一班男生有a人,女生有b人,一共有(a+b)人。
s=vt
V=Sh
a+b=b+a
ABBABBABB……
你会用字母表示什么?请在下表中写出来。
1.
五、
用字母表示计算方法。
用字母表示除法、分数或比时,表示除数、分母以及
比的后项的字母不能是0。
用字母表示运算结果时,必须是最简明的式子。
想一想,在一个含有字母的式子里,数与字母、
字母与字母相乘,书写时应注意什么?
2.
字母与字母、字母与数字之间的乘号可以记
作“·”或省略不写。但要注意,在省略乘号的
时候,应当把数字写在字母的前面。
如:
a·b
3x
方程与等式有什么区别和联系?
3.
为了求未知数,利用某种数量关系在已知数与未知数
之间建立的等式关系就是方程。
表示相等关系的式子叫作等式。
(1)
方程必须是等式,等式不一定是方程。
(2)
方程必须含有未知数,等式可以不含有未知数。
等式
方程
你能举例说明等式的性质吗?
4.
(1)
等式两边加上或减去同一个数,左右两边仍
然相等。如:
(2)
等式两边乘同一个数,或除以同一个不为0的
数,左右两边仍然相等。如:
3×4=2×6
3×4+4=2×6+4
3×4=2×6
3×4×4=2×6×4
3×4÷4=2×6÷4
用方程解决实际问
题,有什么特点?
(1)
弄清题意,找出未知
数,并用字母x表示
(也可以间接设某个量为x,再通过这个量去
求未知数)。
(2)
分析实际问题中的数量关系,找出等量关系,并
列出方程。
(3)
解方程,求出未知数的值。
(4)
检验方程的解是否符合题意,并写出答语。
随堂练习
(教科书第81页上方做一做)
1.
连线。
比a多3的数
比a少3的数
3个a相加的和
3个a相乘的积
a的3倍
a3
3a
a+3
a?3
2.
(教科书第81页下方做一做)
解:设小云踢了x下。
x=56
答:小云踢了56下。
培优训练
一个学生在爬山中,上山、下山共用了4小时。如
果她上山用了2.4小时,原路返回时下山的速度是
15千米/时,求她上山的速度。
1.
解:设她上山的速度为xkm/h。
2.4x=(4?2.4)×15
2.4x=24
x=10
答:她上山的速度是10km/h。
2.
甲、乙两车都从A城开往B城,甲车每小时行80
千米,乙车每小时行60千米。乙车先行驶2小时
后,甲车才开始出发,多少小时后甲车追上乙车?
解:设x小时后甲车追上乙车。
(80?60)x=2×60
20x=120
x=6
答:6小时后甲车追上乙车。
3.
用一根绳子测井深,将绳4折,井外还余8尺;将绳
6折,正好等于井深,绳长几尺?井深几尺?
解:设井深x尺,则绳长6x尺。
6x=4x+8
2x=8
x=4
答:绳长24尺,井深4尺。
6x=24
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
