人教版六年级数学下册6 整理与复习 统计与概率第2课时 可能性 课件(16张ppt)
文档属性
| 名称 | 人教版六年级数学下册6 整理与复习 统计与概率第2课时 可能性 课件(16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-11 11:22:52 | ||
图片预览






文档简介
整理和复习
3 统计与概率
6
第2课时 可能性
情境导入
明天可能
下雨,可能是
晴天,可能多
云……
新课探究
(教科书第97页)
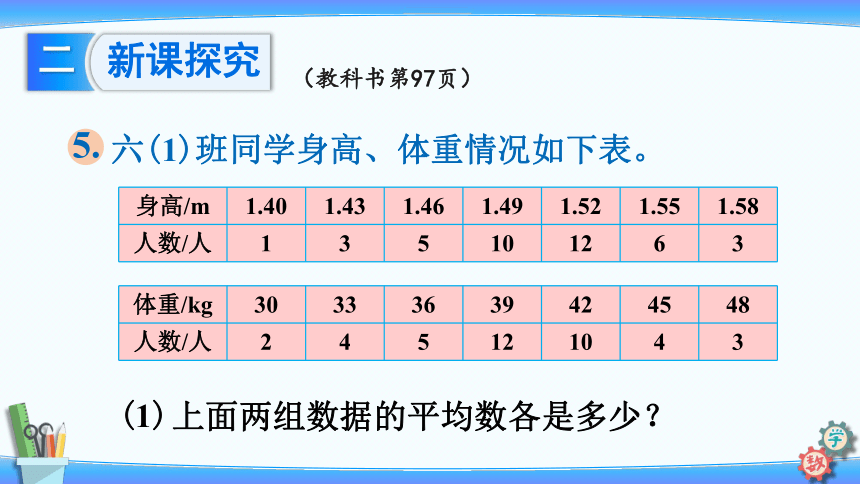
六(1)班同学身高、体重情况如下表。
5.
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数/人
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数/人
2
4
5
12
10
4
3
(1)
上面两组数据的平均数各是多少?
身高平均数:
(1.40×1+1.43×3+1.46×5+1.49×10+1.52×12
+1.55×6+1.58×3)÷(1+3+5+10+12+6+3)
=60.17÷40≈1.50(m)
体重平均数:
(30×2+33×4+36×5+39×12+42×10+45×4
+48×3)÷(2+4+5+12+10+4+3)=1584÷40
=39.6(kg)
(1)
意义:若干个数相加的和除以这些数的个数所
得的结果是这些数的平均数。
(2)
特点:平均数是表示一组数据集中趋势的数,
它是反映数据集中趋势的一项指标。
平均数
(3)
求法:求平均数的基本数量关系式是:总数量
÷总份数=平均数。解题关键是根据已知条件
确定总数量及与它相对应的总份数。
(2)
小组讨论,什么数据能代表全班同学的身高和
体重?
观察两组数据发现,最大与最小相差都不
是很大,且每组数据都是中间段的人数居多,
所以可以用平均数1.50m和39.6kg代表全班同
学的身高和体重。
(3)
如果把全班同学编号,随意抽取一名学生,该生体
重在36kg及以下的可能性大?还是在39kg及以上的可能
性大?
(1)
确定事件和不确定时间
生活中,有些事件的发生是不确定的,一般用
“可能发生”来描述;有些事件的发生是确定
的,一般用“一定发生”或“不可能发生”来
描述。
(2)
事件发生的可能性有大有小,要设计公平的游
戏规则,就要使可能性的大小相等。
可能性
(3)
(4)
计算简单事件发生的可能性的大小,有助于我
们做出预测和决策。
有三位好朋友都参加了绘画比赛,第一位
与第二位的平均成绩是17分,第二位与第
三位的平均成绩是20分,第三位和第一位
的成绩相差几分?
1.
随堂练习
20×2?17×2=6(分)
答:第三位和第一位的成绩相差6分。
袋子中装有8个白球,1个黑球和3个红球。
2.
(1)
从袋中任意摸出一个球,球的颜色有几种可能
的结果?
(2)
摸到哪种颜色的球的可能性最大?
答:球的颜色有3种可能的结果。
答:摸到白球的可能性最大。
培优训练
玩牌游戏。
1.
游戏规则:将4张牌洗匀后反扣在桌面上,任意
摸2张,如果两张牌上的数字之和大于15,算甲方赢;
如果小于15,算乙方赢;如果等于15,则重新摸。这
个游戏规则公平吗?为什么?
答:这个游戏规则公平。
因为任意摸两张牌,数字之和大于15的
有一种结果,小于15的也只有一种结果,双
方获胜的可能性相同。
把10个写有数字的乒乓球装入一个纸箱
中,要使摸出“2”的可能性大于摸出
“10”的可能性,摸出“6”的可能性小
于摸出“10”的可能性,球上的数字应
该怎样写?
2.
提示:数字2比10多,数字10比6多。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
3 统计与概率
6
第2课时 可能性
情境导入
明天可能
下雨,可能是
晴天,可能多
云……
新课探究
(教科书第97页)
六(1)班同学身高、体重情况如下表。
5.
身高/m
1.40
1.43
1.46
1.49
1.52
1.55
1.58
人数/人
1
3
5
10
12
6
3
体重/kg
30
33
36
39
42
45
48
人数/人
2
4
5
12
10
4
3
(1)
上面两组数据的平均数各是多少?
身高平均数:
(1.40×1+1.43×3+1.46×5+1.49×10+1.52×12
+1.55×6+1.58×3)÷(1+3+5+10+12+6+3)
=60.17÷40≈1.50(m)
体重平均数:
(30×2+33×4+36×5+39×12+42×10+45×4
+48×3)÷(2+4+5+12+10+4+3)=1584÷40
=39.6(kg)
(1)
意义:若干个数相加的和除以这些数的个数所
得的结果是这些数的平均数。
(2)
特点:平均数是表示一组数据集中趋势的数,
它是反映数据集中趋势的一项指标。
平均数
(3)
求法:求平均数的基本数量关系式是:总数量
÷总份数=平均数。解题关键是根据已知条件
确定总数量及与它相对应的总份数。
(2)
小组讨论,什么数据能代表全班同学的身高和
体重?
观察两组数据发现,最大与最小相差都不
是很大,且每组数据都是中间段的人数居多,
所以可以用平均数1.50m和39.6kg代表全班同
学的身高和体重。
(3)
如果把全班同学编号,随意抽取一名学生,该生体
重在36kg及以下的可能性大?还是在39kg及以上的可能
性大?
(1)
确定事件和不确定时间
生活中,有些事件的发生是不确定的,一般用
“可能发生”来描述;有些事件的发生是确定
的,一般用“一定发生”或“不可能发生”来
描述。
(2)
事件发生的可能性有大有小,要设计公平的游
戏规则,就要使可能性的大小相等。
可能性
(3)
(4)
计算简单事件发生的可能性的大小,有助于我
们做出预测和决策。
有三位好朋友都参加了绘画比赛,第一位
与第二位的平均成绩是17分,第二位与第
三位的平均成绩是20分,第三位和第一位
的成绩相差几分?
1.
随堂练习
20×2?17×2=6(分)
答:第三位和第一位的成绩相差6分。
袋子中装有8个白球,1个黑球和3个红球。
2.
(1)
从袋中任意摸出一个球,球的颜色有几种可能
的结果?
(2)
摸到哪种颜色的球的可能性最大?
答:球的颜色有3种可能的结果。
答:摸到白球的可能性最大。
培优训练
玩牌游戏。
1.
游戏规则:将4张牌洗匀后反扣在桌面上,任意
摸2张,如果两张牌上的数字之和大于15,算甲方赢;
如果小于15,算乙方赢;如果等于15,则重新摸。这
个游戏规则公平吗?为什么?
答:这个游戏规则公平。
因为任意摸两张牌,数字之和大于15的
有一种结果,小于15的也只有一种结果,双
方获胜的可能性相同。
把10个写有数字的乒乓球装入一个纸箱
中,要使摸出“2”的可能性大于摸出
“10”的可能性,摸出“6”的可能性小
于摸出“10”的可能性,球上的数字应
该怎样写?
2.
提示:数字2比10多,数字10比6多。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
