2020-2021学年冀教新版九年级下册数学《第30章 二次函数》单元测试卷(word有答案)
文档属性
| 名称 | 2020-2021学年冀教新版九年级下册数学《第30章 二次函数》单元测试卷(word有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 183.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 22:18:00 | ||
图片预览




文档简介
2020-2021学年冀教新版九年级下册数学《第30章
二次函数》单元测试卷
一.选择题
1.下列各式中,y是关于x的二次函数的是( )
A.x2y+x=1
B.x2﹣xy=5
C.y2=x2+2
D.x2+y+2=0
2.在二次函数y=x2﹣3x﹣2的图象上的点是( )
A.(1,1)
B.(0,2)
C.(2,﹣4)
D.(﹣1,3)
3.二次函数的一般形式为( )
A.y=ax2+bx+c
B.y=ax2+bx+c(a≠0)
C.y=ax2+bx+c(b2﹣4ac≥0)
D.y=ax2+bx+c(b2﹣4ac=0)
4.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
5.如果二次函数y=ax2+m的值恒大于0,那么必有( )
A.a>0,m取任意实数
B.a>0,m>0
C.a<0,m>0
D.a,m均可取任意实数
6.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2=( )
A.﹣1.3
B.﹣2.3
C.﹣0.3
D.﹣3.3
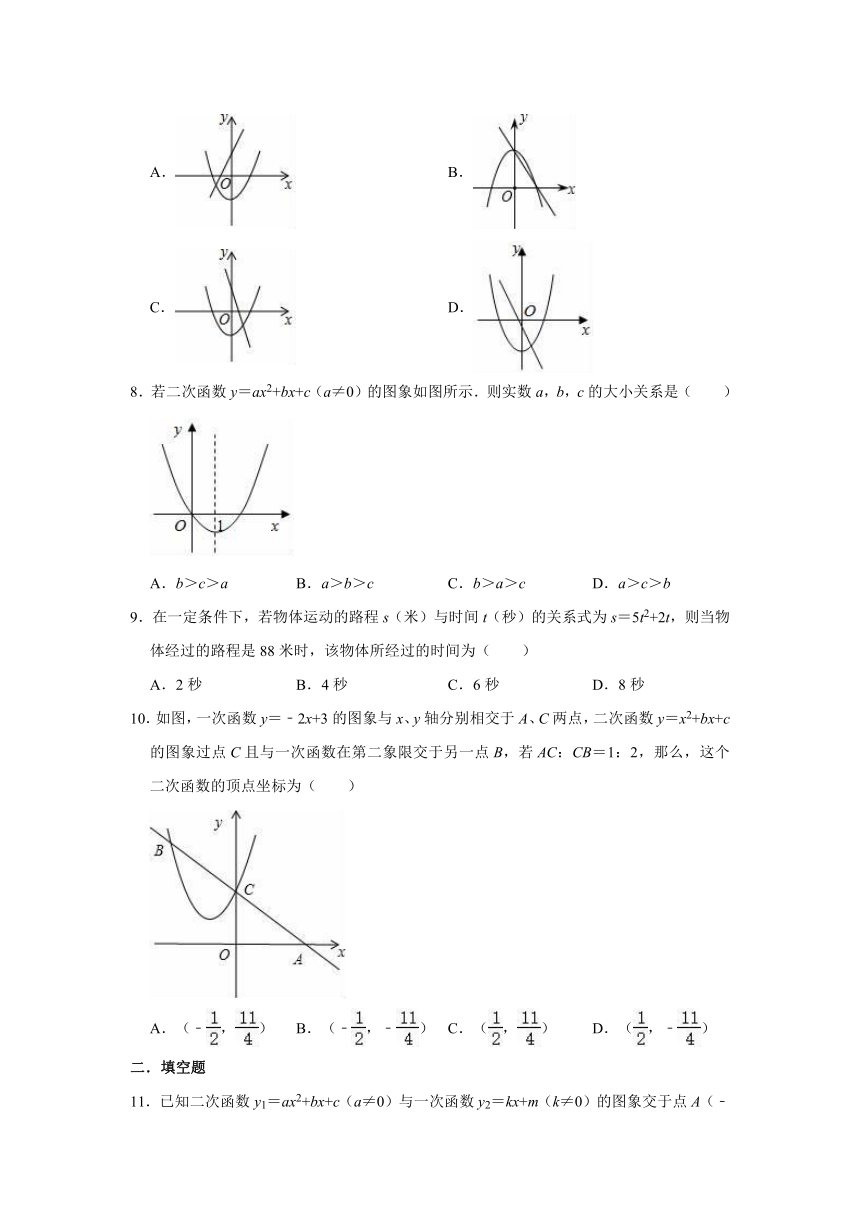
7.函数y=ax2+c与y=ax+c(a≠0)在同一坐标系内的图象是图中的( )
A.
B.
C.
D.
8.若二次函数y=ax2+bx+c(a≠0)的图象如图所示.则实数a,b,c的大小关系是( )
A.b>c>a
B.a>b>c
C.b>a>c
D.a>c>b
9.在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当物体经过的路程是88米时,该物体所经过的时间为( )
A.2秒
B.4秒
C.6秒
D.8秒
10.如图,一次函数y=﹣2x+3的图象与x、y轴分别相交于A、C两点,二次函数y=x2+bx+c的图象过点C且与一次函数在第二象限交于另一点B,若AC:CB=1:2,那么,这个二次函数的顶点坐标为( )
A.(﹣,)
B.(﹣,﹣)
C.(,)
D.(,﹣)
二.填空题
11.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(﹣1,4),B(6,2)(如图所示),则能使y1>y2成立的x的取值范围是
.
12.抛物线y=ax2与直线y=3x+b只有一个公共点,则b=
.
13.把y=3x2+6x﹣3化为y=a(x﹣h)2+k的形式,y=
.对称轴是
,顶点坐标是
.
14.将二次函数y=x2﹣2x的图象向上平移3个单位长度,再向右平移4个单位长度得到的新的图象相应的函数关系式是
.
15.已知a>0,b<0,则抛物线y=ax2+bx的图象经过第
象限.
16.已知二次函数y=x2﹣2x﹣8的图象与x轴交于A、B两点,与y轴交于C点,则△ABC的面积为
.
17.某旅行社有100张床位,每床每日收费10元,客床可全部租出,若每床每日收费提高2元,则租出床位减少10张.若每床每日收费再提高2元,则租出床位再减少10张.以每提高2元的这种方法变化下去,为了投资少而获利大,每床每日应提高
元.
18.半径为r的圆,如果半径增加m,那么新圆的面积S与m之间的函数关系式是
.
19.请写出一个以(2,3)为顶点,且开口向上的二次函数
.
20.已知反比例函数y=的图象经过点P(2,2),函数y=ax+b的图象与直线y=﹣x平行,并且经过反比例函数图象上一点Q(1,m).则函数y=ax2+bx+有最
值,这个值是
.
三.解答题
21.画出函数y=﹣x2+2x+3的图象,观察图象说明:当x取何值时,y<0,当x取何值时,y>0.
22.某商店购进了一种小商品,每件进价为2元.经市场预测,销售定价为3元时,可售出200件;现为了减少库存,商店决定采取适当降价措施.经调查发现,销售定价每降低0.1元时,销售量将增多40件.
(1)商店若希望获利224元,则应该降价多少元?
(2)商店若要获得最大利润,应降价多少元?最大利润是多少?
23.已知是x的二次函数,求出它的解析式.
24.对于抛物线y=x2+bx+c,给出以下陈述:
①它的对称轴为x=2;
②它与x轴有两个交点为A、B;
③△APB的面积不小于27(P为抛物线的顶点).
求①、②、③得以同时成立时,常数b、c的取值范围.
25.已知二次函数y=﹣2x2,怎样平移这个函数的图象,才能使它经过(0,1)和(1,3)两点?写出平移后的函数解析式.
26.已知二次函数y=﹣x2+4x.
(1)用配方法或公式法把该函数化为y=a(x+m)2+k(其中a、m、k都是常数且a≠0)的形式,并指出函数图象的开口方向,对称轴和顶点坐标;
(2)当x满足什么条件时,函数值随着自变量的增大而减小?
27.已知二次函数y=x2﹣(m2+8)x+2(m2+6),设抛物线顶点为A,与x轴交于B、C两点,问是否存在实数m,使△ABC为等腰直角三角形?如果存在求m;若不存在说明理由.
参考答案与试题解析
一.选择题
1.解:A、整理后,不符合二次函数的一般形式,错误;
B、整理后,不符合二次函数的一般形式,错误;
C、这里,y的指数是2,不是函数,错误;
D、整理为y=﹣x2﹣2,是二次函数,正确.
故选:D.
2.解:A、x=1时,y=1﹣3﹣2=﹣4,不符合;
B、x=0时,y=﹣2,不符合;
C、x=2时,y=4﹣6﹣2=﹣4,满足;
D、x=﹣1时,y=1+3﹣2=2,不符合;
故选:C.
3.解:根据一元二次方程的一般形式的概念知,应为y=ax2+bx+c(a≠0,a、b、c为常数),
故选:B.
4.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
5.解:由题意得:二次函数y=ax2+m的最小值大于0,
∴a>0,m>0,
故选:B.
6.解:方法一:
∵二次函数y=ax2+bx+c的顶点坐标(﹣1,﹣3.2)
∴﹣=﹣1则﹣=﹣2
∵x1x2是一元二次方程ax2+bx+c=0的两根
∴x1+x2=﹣
又∵x1=1.3
∴x1+x2=1.3+x2=﹣2
解得x2=﹣3.3.
方法二:
根据对称轴为;x=﹣1,关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3,
则=﹣1,即=﹣1,
解得:x2=﹣3.3,
故选:D.
7.解:A、由函数y=ax+c的图象可得:a>0,c>0,由二次函数y=ax2+c的图象可得:a>0,c<0,错误;
B、由函数y=ax+c的图象可得:a<0,c>0,由二次函数y=ax2+c的图象可得:a<0,c>0,且与y轴交于同一点,正确;
C、由函数y=ax+c的图象可得:a<0,c>0,由二次函数y=ax2+c图象可得:a>0,c<0,错误;
D、由函数y=ax+c的图象可得:a<0,c<0,由二次函数y=ax2+c的图象可得:a>0,c<0,错误.
故选:B.
8.解:∵图象开口向上,经过原点,对称轴在y轴右侧,
∴a>0,c=0,﹣=1,
∴b=﹣2a<0,
∴a>c>b,
故选:D.
9.解:把s=88代入s=5t2+2t得:
5t2+2t=88.
解得t1=4,t2=﹣4.4(舍去),即t=4秒.
故选:B.
10.解:由图象y=﹣2x+3知:C(0,3),A(1.5,0)
即c=3,
因为y=x2+bx+3,可设B(a,a2+ba+3),
又∵B在函数y=﹣2x+3的图象上则有a2+ba+3=﹣2a+3…(1),
又∵AC:CB=1:2,…(2),则由(1)和(2)解得:a=﹣3,b=1(负值已舍).
由顶点坐标(﹣,)得(﹣).
故选:A.
二.填空题
11.解:∵两函数图象的交点坐标为A(﹣1,4),B(6,2),
∴使y1>y2成立的x的取值范围是x<﹣1或x>6.
故答案为:x<﹣1或x>6.
12.解:∵抛物线y=ax2与直线y=3x+b只有一个公共点,
∴ax2=3x+b只有一个解,
即ax2﹣3x﹣b=0只有一个解,
∴△=9+4ab=0.
解得b=﹣.
13.解:y=3x2﹣6x﹣3=3(x2+2x+1)﹣6=3(x+1)2﹣6,
对称轴是直线x=﹣1,顶点坐标是(﹣1,﹣6).
故答案是3(x+1)2﹣6,直线x=﹣1,(﹣1,﹣6).
14.解:y=x2﹣2x=(x﹣1)2﹣1,即二次函数y=x2﹣2x的图象的顶点坐标为(1,﹣1),
把点(1,﹣1)向上平移3个单位长度,再向右平移4个单位长度得到的点的坐标为(5,2),
所以新的图象相应的函数关系式是y=(x﹣5)2+2.
故答案为y=(x﹣5)2+2.
15.解:∵a>0,
∴开口方向向上,
∵b<0,a>0,
∴对称轴x=﹣>0,
∵c=0,
∴此函数过原点.
∴它的图象经过一、二、四象限.
故答案为:一、二、四.
16.解:根据二次函数y=x2﹣2x﹣8,可得A、B两点的横坐标为﹣2,4;
C的纵坐标为﹣8;
则△ABC的面积为×8×6=24.
17.解:设每床每日应提高x元,每日获利为y元,
则y=(10+x)(100﹣?10)=﹣5(x﹣5)2+1125(0≤x<20)
∵a=﹣5<0,
∴函数图象知:开口向下,二次函数有最大值,
∴为了投资少而获利大,当x=6时,每日获利y最大.
故填6元.
18.解:新圆的半径是(r+m),则S与m之间的函数关系式是:S=π(r+m)2.
19.解:由抛物线开口向上,取a=1,
已知顶点坐标为(2,3),
所以,抛物线解析式可写为
y=(x﹣2)2+3.
20.解:根据反比例函数y=的图象经过点P(2,2),
得k=2×2=4;
根据函数y=ax+b的图象与直线y=﹣x平行,得到a=﹣1;
根据经过反比例函数图象上一点Q(1,m),
首先得到m=4,再进一步得到b=5,则二次函数的解析式是y=﹣x2+5x﹣.
根据顶点公式求得它的顶点坐标是(,1),
因为a<0,
所以它有最大值是1.
三.解答题
21.解:∵y=﹣x2+2x+3,
=﹣(x﹣1)2+4,
∴开口方向向下,对称轴x=1,顶点坐标(1,4),
令x=0得:y=3,
∴与y轴交点坐标(0,3),
令y=0得:﹣x2+2x+3=0,
∴x1=1
x2=3,
∴与x轴交点坐标(﹣1,0),(3,0),
作出函数如图所示的图象,
由图象可以看出:当x<﹣1或x>3时,y<0;
当﹣1<x<3时,y>0.
22.解:(1)设每件小商品应该降价x元,则可售出(200+400x)件,
依题意,得:(3﹣2﹣x)(200+400x)=224,
整理,得:2x2﹣x+0.12=0,
解得:x1=0.3,x2=0.2,
∵为了减少库存,
∴x=0.3,
答:商店若希望获利224元,则应该降价0.3元;
(2)设每件应降价y元,利润为w元,
w=(3﹣2﹣y)(200+400y)=﹣400y2+200y+200=﹣400(y﹣0.25)2+225,
∴当y=0.25时,w取得最大值,此时w=225,
即商店若要获得最大利润,应降价0.25元,最大利润是225元.
23.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
24.解:∵抛物线y=x2+bx+c=(x+)2+,抛物线y=x2+bx+c的对称轴为x=2,
∴﹣=2,则b=﹣4,
∴P点的纵坐标是=c﹣4,
又∵它与x轴有两个交点为A、B,
∴△=b2﹣4ac=16﹣4c>0,且AB===2
解得
c<4,①
又△APB的面积不小于27,
∴×2×|c﹣4|≥27,即×|c﹣4|≥27②
由①②解得
c≤﹣5.
综上所述,b的值是﹣4,c的取值范围是c≤﹣5.
25.解:设y=﹣2x2+bx+c,把(0,1)(1,3)代入,
得c=1,﹣2+b+c=3,
解得b=4.
∴平移后的函数解析式为y=﹣2x2+4x+1=﹣2(x﹣1)2+3.
∵原抛物线的顶点为(0,0),
∴新抛物线的顶点为(1,3).
∴将原二次函数y=﹣2x2先向右平移1个单位,再向上平移3个单位,可得y=﹣2x2+4x+1的图象.
26.解:(1)y=﹣(x2﹣4x),
=﹣(x2﹣4x+4)+4,
=﹣(x﹣2)2+4,
对称轴为直线x=2,顶点坐标为(2,4);
(2)∵y=﹣(x﹣2)2+4,a<0,对称轴为直线x=2,
∴当x>2时,函数值y随着自变量x的增大而减小.
27.解:若△ABC是等腰直角三角形,则∠BAC=90°,
设B、C两点的坐标分别为(x1,0)、(x2,0),x1<x2,则x1、x2是方程x2﹣(m2+8)x+2(m2+6)=0的两个根,
∴x1+x2=m2+8,x1?x2=2(m2+6),
∴x1>0,x2>0,
∴BC=x2﹣x1,
∵(x1﹣x2)2=(x1+x2)2﹣4x1x2=(m2+8)2﹣8(m2+6),
=(m2+4)2,
∴BC=m2+4,
∵由抛物线的顶点坐标可知,A点的纵坐标为,
=2(m2+6)﹣,
∴AD=﹣2(m2+6),
∵△ABC是等腰直角三角形,
∴BC=2AD,
∴m2+4=﹣4(m2+6),
解得m2=﹣2<0,m2=﹣4<0,都无意义.
故答案为:不存在实数m,使△ABC为等腰直角三角形.
二次函数》单元测试卷
一.选择题
1.下列各式中,y是关于x的二次函数的是( )
A.x2y+x=1
B.x2﹣xy=5
C.y2=x2+2
D.x2+y+2=0
2.在二次函数y=x2﹣3x﹣2的图象上的点是( )
A.(1,1)
B.(0,2)
C.(2,﹣4)
D.(﹣1,3)
3.二次函数的一般形式为( )
A.y=ax2+bx+c
B.y=ax2+bx+c(a≠0)
C.y=ax2+bx+c(b2﹣4ac≥0)
D.y=ax2+bx+c(b2﹣4ac=0)
4.形状与抛物线y=﹣x2﹣2相同,对称轴是x=﹣2,且过点(0,3)的抛物线是( )
A.y=x2+4x+3
B.y=﹣x2﹣4x+3
C.y=﹣x2+4x+3
D.y=x2+4x+3或y=﹣x2﹣4x+3
5.如果二次函数y=ax2+m的值恒大于0,那么必有( )
A.a>0,m取任意实数
B.a>0,m>0
C.a<0,m>0
D.a,m均可取任意实数
6.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3和x2=( )
A.﹣1.3
B.﹣2.3
C.﹣0.3
D.﹣3.3
7.函数y=ax2+c与y=ax+c(a≠0)在同一坐标系内的图象是图中的( )
A.
B.
C.
D.
8.若二次函数y=ax2+bx+c(a≠0)的图象如图所示.则实数a,b,c的大小关系是( )
A.b>c>a
B.a>b>c
C.b>a>c
D.a>c>b
9.在一定条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当物体经过的路程是88米时,该物体所经过的时间为( )
A.2秒
B.4秒
C.6秒
D.8秒
10.如图,一次函数y=﹣2x+3的图象与x、y轴分别相交于A、C两点,二次函数y=x2+bx+c的图象过点C且与一次函数在第二象限交于另一点B,若AC:CB=1:2,那么,这个二次函数的顶点坐标为( )
A.(﹣,)
B.(﹣,﹣)
C.(,)
D.(,﹣)
二.填空题
11.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象交于点A(﹣1,4),B(6,2)(如图所示),则能使y1>y2成立的x的取值范围是
.
12.抛物线y=ax2与直线y=3x+b只有一个公共点,则b=
.
13.把y=3x2+6x﹣3化为y=a(x﹣h)2+k的形式,y=
.对称轴是
,顶点坐标是
.
14.将二次函数y=x2﹣2x的图象向上平移3个单位长度,再向右平移4个单位长度得到的新的图象相应的函数关系式是
.
15.已知a>0,b<0,则抛物线y=ax2+bx的图象经过第
象限.
16.已知二次函数y=x2﹣2x﹣8的图象与x轴交于A、B两点,与y轴交于C点,则△ABC的面积为
.
17.某旅行社有100张床位,每床每日收费10元,客床可全部租出,若每床每日收费提高2元,则租出床位减少10张.若每床每日收费再提高2元,则租出床位再减少10张.以每提高2元的这种方法变化下去,为了投资少而获利大,每床每日应提高
元.
18.半径为r的圆,如果半径增加m,那么新圆的面积S与m之间的函数关系式是
.
19.请写出一个以(2,3)为顶点,且开口向上的二次函数
.
20.已知反比例函数y=的图象经过点P(2,2),函数y=ax+b的图象与直线y=﹣x平行,并且经过反比例函数图象上一点Q(1,m).则函数y=ax2+bx+有最
值,这个值是
.
三.解答题
21.画出函数y=﹣x2+2x+3的图象,观察图象说明:当x取何值时,y<0,当x取何值时,y>0.
22.某商店购进了一种小商品,每件进价为2元.经市场预测,销售定价为3元时,可售出200件;现为了减少库存,商店决定采取适当降价措施.经调查发现,销售定价每降低0.1元时,销售量将增多40件.
(1)商店若希望获利224元,则应该降价多少元?
(2)商店若要获得最大利润,应降价多少元?最大利润是多少?
23.已知是x的二次函数,求出它的解析式.
24.对于抛物线y=x2+bx+c,给出以下陈述:
①它的对称轴为x=2;
②它与x轴有两个交点为A、B;
③△APB的面积不小于27(P为抛物线的顶点).
求①、②、③得以同时成立时,常数b、c的取值范围.
25.已知二次函数y=﹣2x2,怎样平移这个函数的图象,才能使它经过(0,1)和(1,3)两点?写出平移后的函数解析式.
26.已知二次函数y=﹣x2+4x.
(1)用配方法或公式法把该函数化为y=a(x+m)2+k(其中a、m、k都是常数且a≠0)的形式,并指出函数图象的开口方向,对称轴和顶点坐标;
(2)当x满足什么条件时,函数值随着自变量的增大而减小?
27.已知二次函数y=x2﹣(m2+8)x+2(m2+6),设抛物线顶点为A,与x轴交于B、C两点,问是否存在实数m,使△ABC为等腰直角三角形?如果存在求m;若不存在说明理由.
参考答案与试题解析
一.选择题
1.解:A、整理后,不符合二次函数的一般形式,错误;
B、整理后,不符合二次函数的一般形式,错误;
C、这里,y的指数是2,不是函数,错误;
D、整理为y=﹣x2﹣2,是二次函数,正确.
故选:D.
2.解:A、x=1时,y=1﹣3﹣2=﹣4,不符合;
B、x=0时,y=﹣2,不符合;
C、x=2时,y=4﹣6﹣2=﹣4,满足;
D、x=﹣1时,y=1+3﹣2=2,不符合;
故选:C.
3.解:根据一元二次方程的一般形式的概念知,应为y=ax2+bx+c(a≠0,a、b、c为常数),
故选:B.
4.解:设所求抛物线的函数关系式为y=ax2+bx+c,由抛物线过点(0,3),可得:c=3,
由抛物线形状与y=﹣x2﹣2相同,
分为两种情况:①开口向下,则a<0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b<0,
由此可得出B选项符合题意.
②开口向下,则a>0,
又∵对称轴x=﹣2,则x=﹣=﹣2.则b>0,
由此可得出A选项符合题意,
综合上述,符合条件的是选项D,
故选:D.
5.解:由题意得:二次函数y=ax2+m的最小值大于0,
∴a>0,m>0,
故选:B.
6.解:方法一:
∵二次函数y=ax2+bx+c的顶点坐标(﹣1,﹣3.2)
∴﹣=﹣1则﹣=﹣2
∵x1x2是一元二次方程ax2+bx+c=0的两根
∴x1+x2=﹣
又∵x1=1.3
∴x1+x2=1.3+x2=﹣2
解得x2=﹣3.3.
方法二:
根据对称轴为;x=﹣1,关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=1.3,
则=﹣1,即=﹣1,
解得:x2=﹣3.3,
故选:D.
7.解:A、由函数y=ax+c的图象可得:a>0,c>0,由二次函数y=ax2+c的图象可得:a>0,c<0,错误;
B、由函数y=ax+c的图象可得:a<0,c>0,由二次函数y=ax2+c的图象可得:a<0,c>0,且与y轴交于同一点,正确;
C、由函数y=ax+c的图象可得:a<0,c>0,由二次函数y=ax2+c图象可得:a>0,c<0,错误;
D、由函数y=ax+c的图象可得:a<0,c<0,由二次函数y=ax2+c的图象可得:a>0,c<0,错误.
故选:B.
8.解:∵图象开口向上,经过原点,对称轴在y轴右侧,
∴a>0,c=0,﹣=1,
∴b=﹣2a<0,
∴a>c>b,
故选:D.
9.解:把s=88代入s=5t2+2t得:
5t2+2t=88.
解得t1=4,t2=﹣4.4(舍去),即t=4秒.
故选:B.
10.解:由图象y=﹣2x+3知:C(0,3),A(1.5,0)
即c=3,
因为y=x2+bx+3,可设B(a,a2+ba+3),
又∵B在函数y=﹣2x+3的图象上则有a2+ba+3=﹣2a+3…(1),
又∵AC:CB=1:2,…(2),则由(1)和(2)解得:a=﹣3,b=1(负值已舍).
由顶点坐标(﹣,)得(﹣).
故选:A.
二.填空题
11.解:∵两函数图象的交点坐标为A(﹣1,4),B(6,2),
∴使y1>y2成立的x的取值范围是x<﹣1或x>6.
故答案为:x<﹣1或x>6.
12.解:∵抛物线y=ax2与直线y=3x+b只有一个公共点,
∴ax2=3x+b只有一个解,
即ax2﹣3x﹣b=0只有一个解,
∴△=9+4ab=0.
解得b=﹣.
13.解:y=3x2﹣6x﹣3=3(x2+2x+1)﹣6=3(x+1)2﹣6,
对称轴是直线x=﹣1,顶点坐标是(﹣1,﹣6).
故答案是3(x+1)2﹣6,直线x=﹣1,(﹣1,﹣6).
14.解:y=x2﹣2x=(x﹣1)2﹣1,即二次函数y=x2﹣2x的图象的顶点坐标为(1,﹣1),
把点(1,﹣1)向上平移3个单位长度,再向右平移4个单位长度得到的点的坐标为(5,2),
所以新的图象相应的函数关系式是y=(x﹣5)2+2.
故答案为y=(x﹣5)2+2.
15.解:∵a>0,
∴开口方向向上,
∵b<0,a>0,
∴对称轴x=﹣>0,
∵c=0,
∴此函数过原点.
∴它的图象经过一、二、四象限.
故答案为:一、二、四.
16.解:根据二次函数y=x2﹣2x﹣8,可得A、B两点的横坐标为﹣2,4;
C的纵坐标为﹣8;
则△ABC的面积为×8×6=24.
17.解:设每床每日应提高x元,每日获利为y元,
则y=(10+x)(100﹣?10)=﹣5(x﹣5)2+1125(0≤x<20)
∵a=﹣5<0,
∴函数图象知:开口向下,二次函数有最大值,
∴为了投资少而获利大,当x=6时,每日获利y最大.
故填6元.
18.解:新圆的半径是(r+m),则S与m之间的函数关系式是:S=π(r+m)2.
19.解:由抛物线开口向上,取a=1,
已知顶点坐标为(2,3),
所以,抛物线解析式可写为
y=(x﹣2)2+3.
20.解:根据反比例函数y=的图象经过点P(2,2),
得k=2×2=4;
根据函数y=ax+b的图象与直线y=﹣x平行,得到a=﹣1;
根据经过反比例函数图象上一点Q(1,m),
首先得到m=4,再进一步得到b=5,则二次函数的解析式是y=﹣x2+5x﹣.
根据顶点公式求得它的顶点坐标是(,1),
因为a<0,
所以它有最大值是1.
三.解答题
21.解:∵y=﹣x2+2x+3,
=﹣(x﹣1)2+4,
∴开口方向向下,对称轴x=1,顶点坐标(1,4),
令x=0得:y=3,
∴与y轴交点坐标(0,3),
令y=0得:﹣x2+2x+3=0,
∴x1=1
x2=3,
∴与x轴交点坐标(﹣1,0),(3,0),
作出函数如图所示的图象,
由图象可以看出:当x<﹣1或x>3时,y<0;
当﹣1<x<3时,y>0.
22.解:(1)设每件小商品应该降价x元,则可售出(200+400x)件,
依题意,得:(3﹣2﹣x)(200+400x)=224,
整理,得:2x2﹣x+0.12=0,
解得:x1=0.3,x2=0.2,
∵为了减少库存,
∴x=0.3,
答:商店若希望获利224元,则应该降价0.3元;
(2)设每件应降价y元,利润为w元,
w=(3﹣2﹣y)(200+400y)=﹣400y2+200y+200=﹣400(y﹣0.25)2+225,
∴当y=0.25时,w取得最大值,此时w=225,
即商店若要获得最大利润,应降价0.25元,最大利润是225元.
23.解:由二次函数的定义,可知m2+m≠0,即m≠0,m≠﹣1
又因为m2﹣2m﹣1=2,m2﹣2m﹣3=0
解得m=3或m=﹣1(不合题意,舍去)
所以m=3
故y=12x2+9.
24.解:∵抛物线y=x2+bx+c=(x+)2+,抛物线y=x2+bx+c的对称轴为x=2,
∴﹣=2,则b=﹣4,
∴P点的纵坐标是=c﹣4,
又∵它与x轴有两个交点为A、B,
∴△=b2﹣4ac=16﹣4c>0,且AB===2
解得
c<4,①
又△APB的面积不小于27,
∴×2×|c﹣4|≥27,即×|c﹣4|≥27②
由①②解得
c≤﹣5.
综上所述,b的值是﹣4,c的取值范围是c≤﹣5.
25.解:设y=﹣2x2+bx+c,把(0,1)(1,3)代入,
得c=1,﹣2+b+c=3,
解得b=4.
∴平移后的函数解析式为y=﹣2x2+4x+1=﹣2(x﹣1)2+3.
∵原抛物线的顶点为(0,0),
∴新抛物线的顶点为(1,3).
∴将原二次函数y=﹣2x2先向右平移1个单位,再向上平移3个单位,可得y=﹣2x2+4x+1的图象.
26.解:(1)y=﹣(x2﹣4x),
=﹣(x2﹣4x+4)+4,
=﹣(x﹣2)2+4,
对称轴为直线x=2,顶点坐标为(2,4);
(2)∵y=﹣(x﹣2)2+4,a<0,对称轴为直线x=2,
∴当x>2时,函数值y随着自变量x的增大而减小.
27.解:若△ABC是等腰直角三角形,则∠BAC=90°,
设B、C两点的坐标分别为(x1,0)、(x2,0),x1<x2,则x1、x2是方程x2﹣(m2+8)x+2(m2+6)=0的两个根,
∴x1+x2=m2+8,x1?x2=2(m2+6),
∴x1>0,x2>0,
∴BC=x2﹣x1,
∵(x1﹣x2)2=(x1+x2)2﹣4x1x2=(m2+8)2﹣8(m2+6),
=(m2+4)2,
∴BC=m2+4,
∵由抛物线的顶点坐标可知,A点的纵坐标为,
=2(m2+6)﹣,
∴AD=﹣2(m2+6),
∵△ABC是等腰直角三角形,
∴BC=2AD,
∴m2+4=﹣4(m2+6),
解得m2=﹣2<0,m2=﹣4<0,都无意义.
故答案为:不存在实数m,使△ABC为等腰直角三角形.
