6.2-2实验:探究向心力大小表达式—2020-2021学年【新教材】人教版(2019)高中物理必修第二册学案
文档属性
| 名称 | 6.2-2实验:探究向心力大小表达式—2020-2021学年【新教材】人教版(2019)高中物理必修第二册学案 | 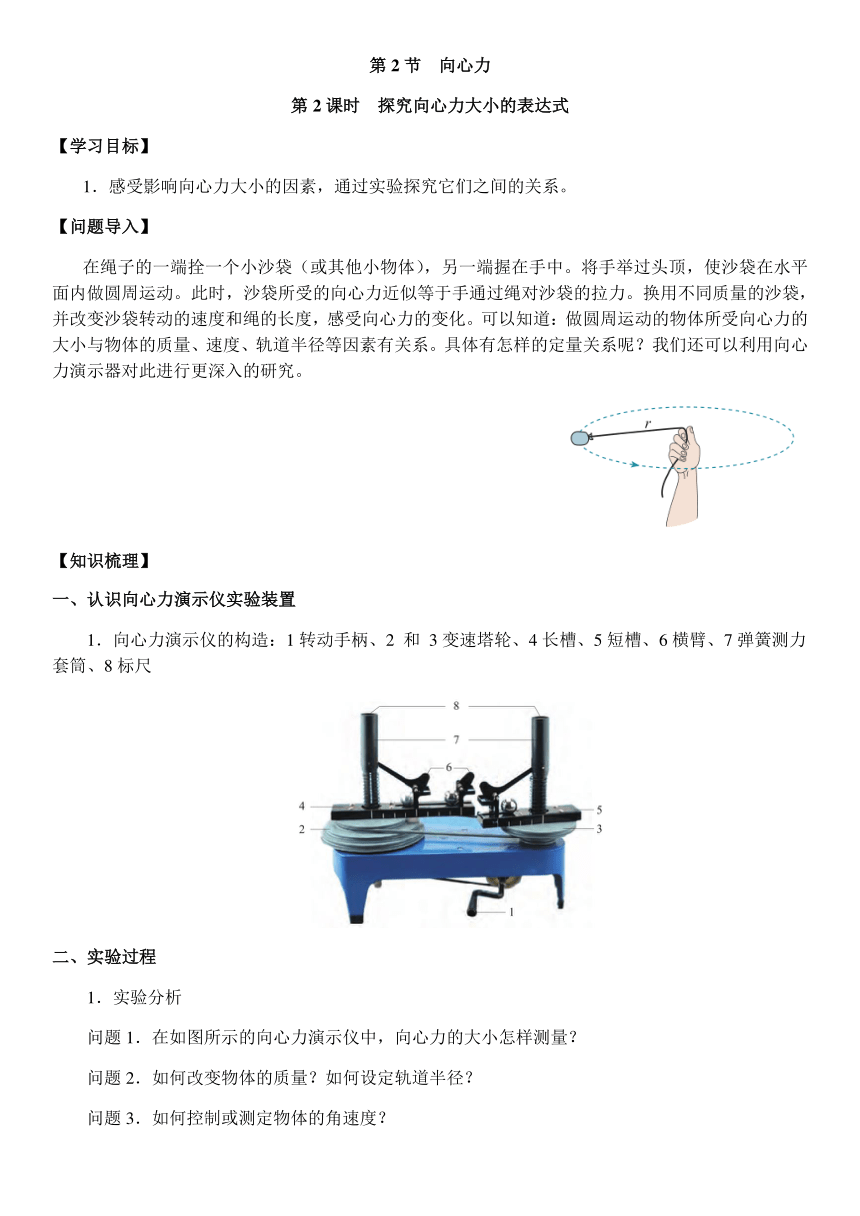 | |
| 格式 | docx | ||
| 文件大小 | 358.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-09 21:37:50 | ||
图片预览


文档简介
第2节 向心力
第2课时
探究向心力大小的表达式
【学习目标】
1.感受影响向心力大小的因素,通过实验探究它们之间的关系。
【问题导入】
在绳子的一端拴一个小沙袋(或其他小物体),另一端握在手中。将手举过头顶,使沙袋在水平面内做圆周运动。此时,沙袋所受的向心力近似等于手通过绳对沙袋的拉力。换用不同质量的沙袋,并改变沙袋转动的速度和绳的长度,感受向心力的变化。可以知道:做圆周运动的物体所受向心力的大小与物体的质量、速度、轨道半径等因素有关系。具体有怎样的定量关系呢?我们还可以利用向心力演示器对此进行更深入的研究。
【知识梳理】
一、认识向心力演示仪实验装置
1.向心力演示仪的构造:1转动手柄、2
和
3变速塔轮、4长槽、5短槽、6横臂、7弹簧测力套筒、8标尺
二、实验过程
1.实验分析
问题1.在如图所示的向心力演示仪中,向心力的大小怎样测量?
问题2.如何改变物体的质量?如何设定轨道半径?
问题3.如何控制或测定物体的角速度?
问题4.你安排的实验步骤是怎样的?
问题5.得到了怎样的实验结果?根据已有知识,你还能写出怎样的表达式
2.实验方法:控制变量法
3.实验过程
(1)保持两个小球质量m和角速度ω相同,使两球运动半径r不同进行实验,比较向心力Fn与运动半径r之间的关系.
(2)保持两个小球质量m和运动半径r相同,使两球的角速度ω不同进行实验,比较向心力Fn与角速度ω之间的关系.
(3)保持运动半径r和角速度ω相同,用质量m不同的钢球和铝球进行实验,比较向心力Fn与质量m的关系.
4.实验结论
两球相同的物理量
不同的物理量
实验结论
1
m、ω
r
r越大,Fn越大,Fn∝r
2
m、r
ω
ω越大,Fn越大,Fn∝ω2
3
r、ω
m
m越大,Fn越大,Fn∝m
精确的实验表明向心力的大小可以表示为Fn=m=mω2r=mr
【学习过程】
1.如图所示,是探究向心力的大小F与质量m、角速度ω和半径r之间的关系的实验装置.转动手柄,可使塔轮、长槽和短槽随之匀速转动.塔轮至上而下有三层,每层左右半径比分别是1∶1、2∶1和3∶1.左右塔轮通过皮带连接,并可通过改变皮带所处的层来改变左右塔轮的角速度之比.实验时,将两个小球分别放在短槽C处和长槽的A(或B)处,A、C到塔轮中心的距离相等.两个小球随塔轮做匀速圆周运动,向心力大小可由塔轮中心标尺露出的等分格的格数读出.
(1)在该实验中应用了
来探究向心力的大小与质量m、角速度ω和半径r之间的关系.
A.理想实验法 B.控制变量法 C.等效替代法
(2)用两个质量相等的小球放在A、C位置,匀速转动时,左边标尺露出1格,右边标尺露出4格,则皮带连接的左、右塔轮半径之比为
.
2.如图所示为一种“滚轮—平盘无极变速器”的示意图,它由固定于主动轴上的平盘和可随从动轴移动的圆柱形滚轮组成.由于摩擦的作用,当平盘转动时,滚轮就会跟随转动,如果认为滚轮不会打滑,那么主动轴转速n1、从动轴转速n2、滚轮半径r以及滚轮中心距离主动轴轴线的距离x之间的关系是( )
A.n2=n1
B.n2=n1
C.n2=n1
D.n2=n1
3.如图所示,长L
的轻杆两端分别固定着可以视为质点的小球A、B,放置在光滑水平桌面上,杆中心O有一竖直方向的固定转动轴,小球A、B
的质量分别为3m、m。当轻杆以角速度ω
绕轴在水平桌面上转动时,求转轴受杆拉力的大小。
4.(多选)如图所示,在光滑水平面上钉有两个钉子A和B,一根长细绳的一端系一个小球,另一端固定在钉子A上,开始时小球与钉子A、B均在一条直线上(图示位置),且细绳的一大部分沿俯视顺时针方向缠绕在两钉子上,现使小球以初速度v0在水平面上沿俯视逆时针方向做匀速圆周运动,使两钉子之间缠绕的绳子逐渐释放,在绳子完全被释放后与释放前相比,下列说法正确的是( )
A.小球的线速度变大
B.小球的角速度变大
C.小球的向心力变小
D.细绳对小球的拉力变小
5.如图所示,一个圆盘在水平面内匀速转动,角速度是
4
rad/s。盘面上距圆盘中心0.10
m
的位置有一个质量为
0.10
kg
的小物体在随圆盘一起做匀速圆周运动。求小物体所受向心力的大小。
【答案提示】
1.答案:(1)B (2)2∶1
2.答案:
A
3.答案:
mω2L
4.答案:
CD
3.答案:
0.16N
第2课时
探究向心力大小的表达式
【学习目标】
1.感受影响向心力大小的因素,通过实验探究它们之间的关系。
【问题导入】
在绳子的一端拴一个小沙袋(或其他小物体),另一端握在手中。将手举过头顶,使沙袋在水平面内做圆周运动。此时,沙袋所受的向心力近似等于手通过绳对沙袋的拉力。换用不同质量的沙袋,并改变沙袋转动的速度和绳的长度,感受向心力的变化。可以知道:做圆周运动的物体所受向心力的大小与物体的质量、速度、轨道半径等因素有关系。具体有怎样的定量关系呢?我们还可以利用向心力演示器对此进行更深入的研究。
【知识梳理】
一、认识向心力演示仪实验装置
1.向心力演示仪的构造:1转动手柄、2
和
3变速塔轮、4长槽、5短槽、6横臂、7弹簧测力套筒、8标尺
二、实验过程
1.实验分析
问题1.在如图所示的向心力演示仪中,向心力的大小怎样测量?
问题2.如何改变物体的质量?如何设定轨道半径?
问题3.如何控制或测定物体的角速度?
问题4.你安排的实验步骤是怎样的?
问题5.得到了怎样的实验结果?根据已有知识,你还能写出怎样的表达式
2.实验方法:控制变量法
3.实验过程
(1)保持两个小球质量m和角速度ω相同,使两球运动半径r不同进行实验,比较向心力Fn与运动半径r之间的关系.
(2)保持两个小球质量m和运动半径r相同,使两球的角速度ω不同进行实验,比较向心力Fn与角速度ω之间的关系.
(3)保持运动半径r和角速度ω相同,用质量m不同的钢球和铝球进行实验,比较向心力Fn与质量m的关系.
4.实验结论
两球相同的物理量
不同的物理量
实验结论
1
m、ω
r
r越大,Fn越大,Fn∝r
2
m、r
ω
ω越大,Fn越大,Fn∝ω2
3
r、ω
m
m越大,Fn越大,Fn∝m
精确的实验表明向心力的大小可以表示为Fn=m=mω2r=mr
【学习过程】
1.如图所示,是探究向心力的大小F与质量m、角速度ω和半径r之间的关系的实验装置.转动手柄,可使塔轮、长槽和短槽随之匀速转动.塔轮至上而下有三层,每层左右半径比分别是1∶1、2∶1和3∶1.左右塔轮通过皮带连接,并可通过改变皮带所处的层来改变左右塔轮的角速度之比.实验时,将两个小球分别放在短槽C处和长槽的A(或B)处,A、C到塔轮中心的距离相等.两个小球随塔轮做匀速圆周运动,向心力大小可由塔轮中心标尺露出的等分格的格数读出.
(1)在该实验中应用了
来探究向心力的大小与质量m、角速度ω和半径r之间的关系.
A.理想实验法 B.控制变量法 C.等效替代法
(2)用两个质量相等的小球放在A、C位置,匀速转动时,左边标尺露出1格,右边标尺露出4格,则皮带连接的左、右塔轮半径之比为
.
2.如图所示为一种“滚轮—平盘无极变速器”的示意图,它由固定于主动轴上的平盘和可随从动轴移动的圆柱形滚轮组成.由于摩擦的作用,当平盘转动时,滚轮就会跟随转动,如果认为滚轮不会打滑,那么主动轴转速n1、从动轴转速n2、滚轮半径r以及滚轮中心距离主动轴轴线的距离x之间的关系是( )
A.n2=n1
B.n2=n1
C.n2=n1
D.n2=n1
3.如图所示,长L
的轻杆两端分别固定着可以视为质点的小球A、B,放置在光滑水平桌面上,杆中心O有一竖直方向的固定转动轴,小球A、B
的质量分别为3m、m。当轻杆以角速度ω
绕轴在水平桌面上转动时,求转轴受杆拉力的大小。
4.(多选)如图所示,在光滑水平面上钉有两个钉子A和B,一根长细绳的一端系一个小球,另一端固定在钉子A上,开始时小球与钉子A、B均在一条直线上(图示位置),且细绳的一大部分沿俯视顺时针方向缠绕在两钉子上,现使小球以初速度v0在水平面上沿俯视逆时针方向做匀速圆周运动,使两钉子之间缠绕的绳子逐渐释放,在绳子完全被释放后与释放前相比,下列说法正确的是( )
A.小球的线速度变大
B.小球的角速度变大
C.小球的向心力变小
D.细绳对小球的拉力变小
5.如图所示,一个圆盘在水平面内匀速转动,角速度是
4
rad/s。盘面上距圆盘中心0.10
m
的位置有一个质量为
0.10
kg
的小物体在随圆盘一起做匀速圆周运动。求小物体所受向心力的大小。
【答案提示】
1.答案:(1)B (2)2∶1
2.答案:
A
3.答案:
mω2L
4.答案:
CD
3.答案:
0.16N
