5.1 频数与频率 课件(共28张PPT)
文档属性
| 名称 | 5.1 频数与频率 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 06:50:03 | ||
图片预览






文档简介
(共28张PPT)
5.1
频数与频率
第5章
数据的频数分布
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.理解频率的概念.
2.理解样本容量、频数、频率之间的相互关系,会计算频率.
3.了解频数、频率的一些简单实际应用.
【过程与方法】
通过收集、分析数据的过程,初步作出合理的决策,提高学生处理问题、决策问题的能力.
【情感态度】
让学生体会到“数字化”给人们的生活带来的便利和数学方法.
【教学重点】
1.
频数、频率的概念
2.理解频数、频率的概念并绘制出相应的统计图表,能做出合理的判断和预测。
【教学难点】
1.
数据分组过程比较复杂,往往要考虑多方面的因素.
2.
正确列出统计图表。
情境导入
射击运动员进行射击训练,教练员需要根据前一阶段的得分情况进行分析,这就需要用到频数和频数直方图.
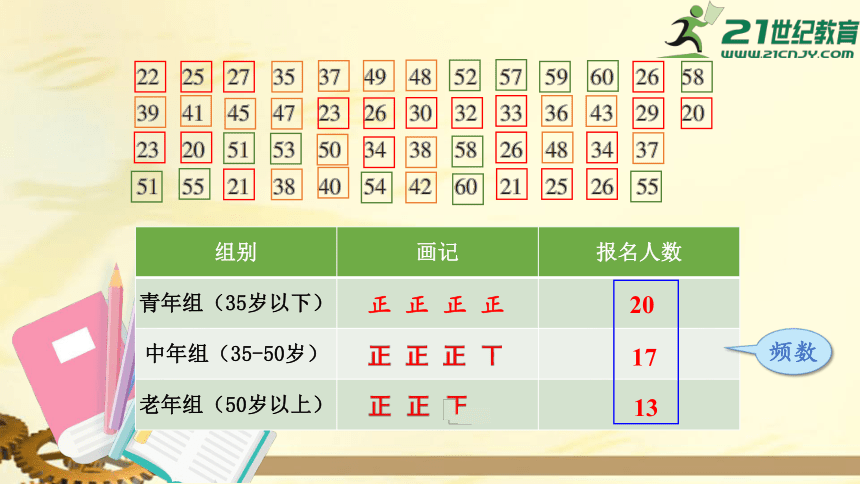
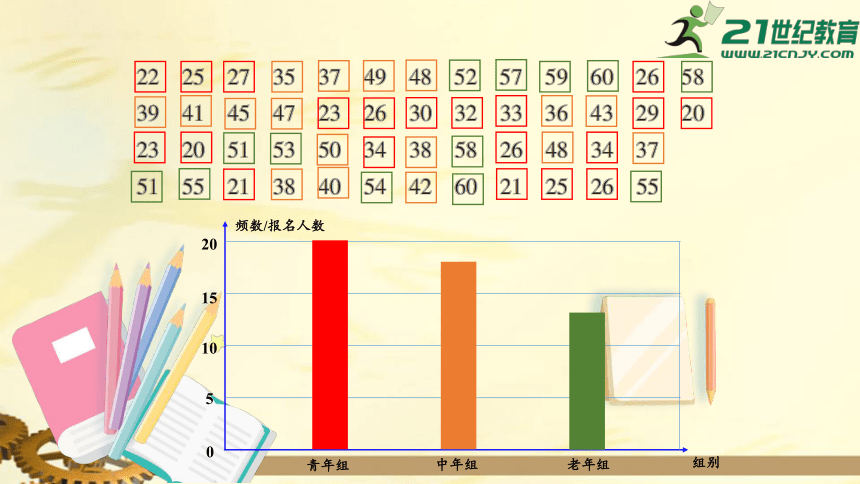
为推广全民健身运动,某单位组织员工进行爬山比赛,50名报名者的年龄如下:
为了公平起见,拟分成青年组(35岁以下)、中年组(35-50岁)、老年组(50岁以上)进行分组竞赛.
请用整理数据的方法,借助统计图表将上述数据进行表述.
探索新知
组别
画记
报名人数
青年组(35岁以下)
中年组(35-50岁)
老年组(50岁以上)
正
正
正
正
20
17
13
频数
频数/报名人数
组别
青年组
中年组
老年组
0
5
10
15
20
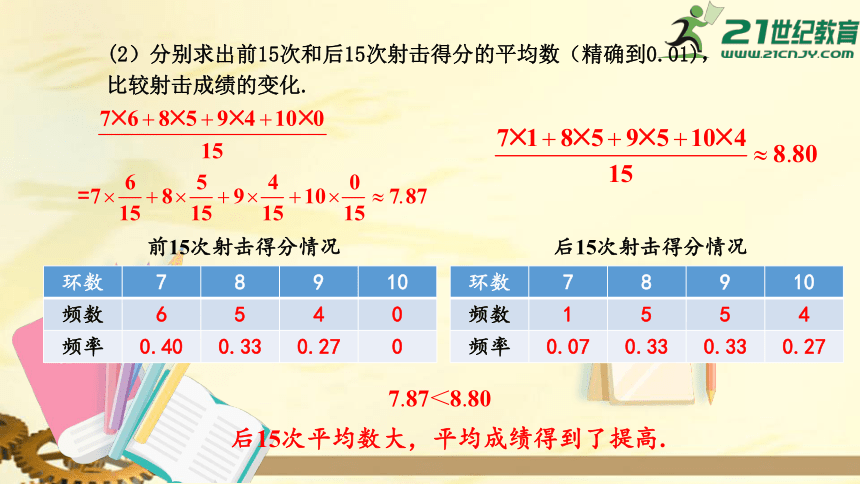
小芳参加校射击队,在一次射击训练中,她先射击了15次,教练对其射击方法作了一些指导后,又射击了15次.她两次射击得分情况如下表所示:
例
(1)用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
环数
7
8
9
10
频数
6
5
4
0
频率
0.40
0.33
0.27
0
前15次射击得分情况
环数
7
8
9
10
频数
1
5
5
4
频率
0.07
0.33
0.33
0.27
后15次射击得分情况
环数
7
8
9
10
频数
6
5
4
0
频率
0.40
0.33
0.27
0
环数
7
8
9
10
频数
1
5
5
4
频率
0.07
0.33
0.33
0.27
前15次射击得分情况
后15次射击得分情况
(2)分别求出前15次和后15次射击得分的平均数(精确到0.01),比较射击成绩的变化.
后15次平均数大,平均成绩得到了提高.
次数
不达标
良
优
频数
1
12
27
频率
0.025
0.3
0.675
(1)
(2)
0.3+0.675=0.975
答:达标率是0.975.
一枚硬币有两面,我们称有国徽的一面为“正面”,另一面为“反面”.掷一枚硬币,当硬币落在桌面时,可能出现“正面朝上”,也可能出现“反面朝上”
.每次掷币,两种情形必然出现一种,也只能出现一种.究竟出现哪种情形,在掷币之前无法预测,只有掷币之后才能知道.
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
(1)计算“正面朝上”和“反面朝上”的频数各是多少,它们之间有什么关系?
(2)计算“正面朝上”和“反面朝上”的频率各是多少,它们之间有什么关系?
假设某同学掷10次的结果如下:
次
数
1
2
3
4
5
6
7
8
9
10
结
果
反
正
正
正
反
反
反
正
反
反
结果
正
反
频数
4
6
频率
0.4
0.6
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比
称为这个试验结果在这n次试验中出现的频率.
课堂练习
一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形:
A.两枚硬币都是“正面朝上”;
B.两枚硬币都是“反面朝上”;
C.一枚硬币“正面朝上”,另一枚硬币“反面朝上”.
每次掷币都发生A,B,C三种情形中的一种,并且只发生一种.
现在全班同学每人各掷两枚硬币5次,记录所得结果,将全班的结果汇总填入下表中,并计算频率.
说一说,出现哪一种情形的频率高?
1.某中学八年级(2)班40名同学投票选举班长,候选人包括陈佳、彭晓、黄敏和汤伟四位.为了方便记录,他们的得票分别以C,P,H,T来代表,投票结果如下:
(1)请根据上述投票结果完成下表:
8
11
9
12
0.2
0.275
0.225
0.3
(2)如果得票最高的候选人被选为班长,则四人中哪一位会当选?
8
11
9
12
0.2
0.275
0.225
0.3
汤伟会当选.
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(1)计算这些车的平均车速.
(40×20+45×30+48×40+50×10+52×10)÷(20+30+40+10+10)
≈46.3km/h
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(2)以哪一个速度行驶的车辆最多?以不超过50km/h的速度行驶的汽车占总监测量的百分之几?
(20+30+40+10)÷(20+30+40+10+10)≈90.9%
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(3)若要对该隧道的通行速度进行限制,你有什么好的建议?
车辆限速45~48km/h(答案不唯一,可根据实际情况确定).
4.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(1)上表中m=_______,
n=______.
(2)在这次抽样调查中,哪类读物最受学生欢迎?哪类读物受欢迎程度最少?
84
0.33
0.14
200
28
84
0.33
4.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(3)若学校计划购买3000册图书,你对购书计划能提出什么好的建议吗?
购书计划:文学类购3000×0.42=1260(册);
艺术类购3000×0.11=330(册);
科普类购3000×0.33=990(册);其他类购3000-1260-330-990=420(册).
0.14
200
28
84
0.33
课堂小结
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比
称为这个试验结果在这n次试验中出现的频率.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
5.1
频数与频率
第5章
数据的频数分布
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.理解频率的概念.
2.理解样本容量、频数、频率之间的相互关系,会计算频率.
3.了解频数、频率的一些简单实际应用.
【过程与方法】
通过收集、分析数据的过程,初步作出合理的决策,提高学生处理问题、决策问题的能力.
【情感态度】
让学生体会到“数字化”给人们的生活带来的便利和数学方法.
【教学重点】
1.
频数、频率的概念
2.理解频数、频率的概念并绘制出相应的统计图表,能做出合理的判断和预测。
【教学难点】
1.
数据分组过程比较复杂,往往要考虑多方面的因素.
2.
正确列出统计图表。
情境导入
射击运动员进行射击训练,教练员需要根据前一阶段的得分情况进行分析,这就需要用到频数和频数直方图.
为推广全民健身运动,某单位组织员工进行爬山比赛,50名报名者的年龄如下:
为了公平起见,拟分成青年组(35岁以下)、中年组(35-50岁)、老年组(50岁以上)进行分组竞赛.
请用整理数据的方法,借助统计图表将上述数据进行表述.
探索新知
组别
画记
报名人数
青年组(35岁以下)
中年组(35-50岁)
老年组(50岁以上)
正
正
正
正
20
17
13
频数
频数/报名人数
组别
青年组
中年组
老年组
0
5
10
15
20
小芳参加校射击队,在一次射击训练中,她先射击了15次,教练对其射击方法作了一些指导后,又射击了15次.她两次射击得分情况如下表所示:
例
(1)用表格表示小芳射击训练中前15次和后15次射击得分的频数和频率.
环数
7
8
9
10
频数
6
5
4
0
频率
0.40
0.33
0.27
0
前15次射击得分情况
环数
7
8
9
10
频数
1
5
5
4
频率
0.07
0.33
0.33
0.27
后15次射击得分情况
环数
7
8
9
10
频数
6
5
4
0
频率
0.40
0.33
0.27
0
环数
7
8
9
10
频数
1
5
5
4
频率
0.07
0.33
0.33
0.27
前15次射击得分情况
后15次射击得分情况
(2)分别求出前15次和后15次射击得分的平均数(精确到0.01),比较射击成绩的变化.
后15次平均数大,平均成绩得到了提高.
次数
不达标
良
优
频数
1
12
27
频率
0.025
0.3
0.675
(1)
(2)
0.3+0.675=0.975
答:达标率是0.975.
一枚硬币有两面,我们称有国徽的一面为“正面”,另一面为“反面”.掷一枚硬币,当硬币落在桌面时,可能出现“正面朝上”,也可能出现“反面朝上”
.每次掷币,两种情形必然出现一种,也只能出现一种.究竟出现哪种情形,在掷币之前无法预测,只有掷币之后才能知道.
与同桌同学合作,掷10次硬币,并把10次试验结果记录下来:
(1)计算“正面朝上”和“反面朝上”的频数各是多少,它们之间有什么关系?
(2)计算“正面朝上”和“反面朝上”的频率各是多少,它们之间有什么关系?
假设某同学掷10次的结果如下:
次
数
1
2
3
4
5
6
7
8
9
10
结
果
反
正
正
正
反
反
反
正
反
反
结果
正
反
频数
4
6
频率
0.4
0.6
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比
称为这个试验结果在这n次试验中出现的频率.
课堂练习
一次掷两枚硬币,用A,B,C分别代表可能发生的三种情形:
A.两枚硬币都是“正面朝上”;
B.两枚硬币都是“反面朝上”;
C.一枚硬币“正面朝上”,另一枚硬币“反面朝上”.
每次掷币都发生A,B,C三种情形中的一种,并且只发生一种.
现在全班同学每人各掷两枚硬币5次,记录所得结果,将全班的结果汇总填入下表中,并计算频率.
说一说,出现哪一种情形的频率高?
1.某中学八年级(2)班40名同学投票选举班长,候选人包括陈佳、彭晓、黄敏和汤伟四位.为了方便记录,他们的得票分别以C,P,H,T来代表,投票结果如下:
(1)请根据上述投票结果完成下表:
8
11
9
12
0.2
0.275
0.225
0.3
(2)如果得票最高的候选人被选为班长,则四人中哪一位会当选?
8
11
9
12
0.2
0.275
0.225
0.3
汤伟会当选.
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(1)计算这些车的平均车速.
(40×20+45×30+48×40+50×10+52×10)÷(20+30+40+10+10)
≈46.3km/h
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(2)以哪一个速度行驶的车辆最多?以不超过50km/h的速度行驶的汽车占总监测量的百分之几?
(20+30+40+10)÷(20+30+40+10+10)≈90.9%
2.某城市交警为检测刚建成通车的城市隧道的通行速度,观测到某时段的来往车辆车速(单位:km/h)如下图所示:
(3)若要对该隧道的通行速度进行限制,你有什么好的建议?
车辆限速45~48km/h(答案不唯一,可根据实际情况确定).
4.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(1)上表中m=_______,
n=______.
(2)在这次抽样调查中,哪类读物最受学生欢迎?哪类读物受欢迎程度最少?
84
0.33
0.14
200
28
84
0.33
4.某中学为了了解学生的课外阅读情况,就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学仅选一项),并根据调查结果制作了下表:
(3)若学校计划购买3000册图书,你对购书计划能提出什么好的建议吗?
购书计划:文学类购3000×0.42=1260(册);
艺术类购3000×0.11=330(册);
科普类购3000×0.33=990(册);其他类购3000-1260-330-990=420(册).
0.14
200
28
84
0.33
课堂小结
一般地,如果重复进行n次试验,某个试验结果出现的次数m称为这个试验结果在这n次试验中出现的频数,而频数与试验总次数的比
称为这个试验结果在这n次试验中出现的频率.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
