人教版小学四年级数学下册 5.3 三角形的内角和 同步测试题 (有答案)
文档属性
| 名称 | 人教版小学四年级数学下册 5.3 三角形的内角和 同步测试题 (有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 79.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 14:01:37 | ||
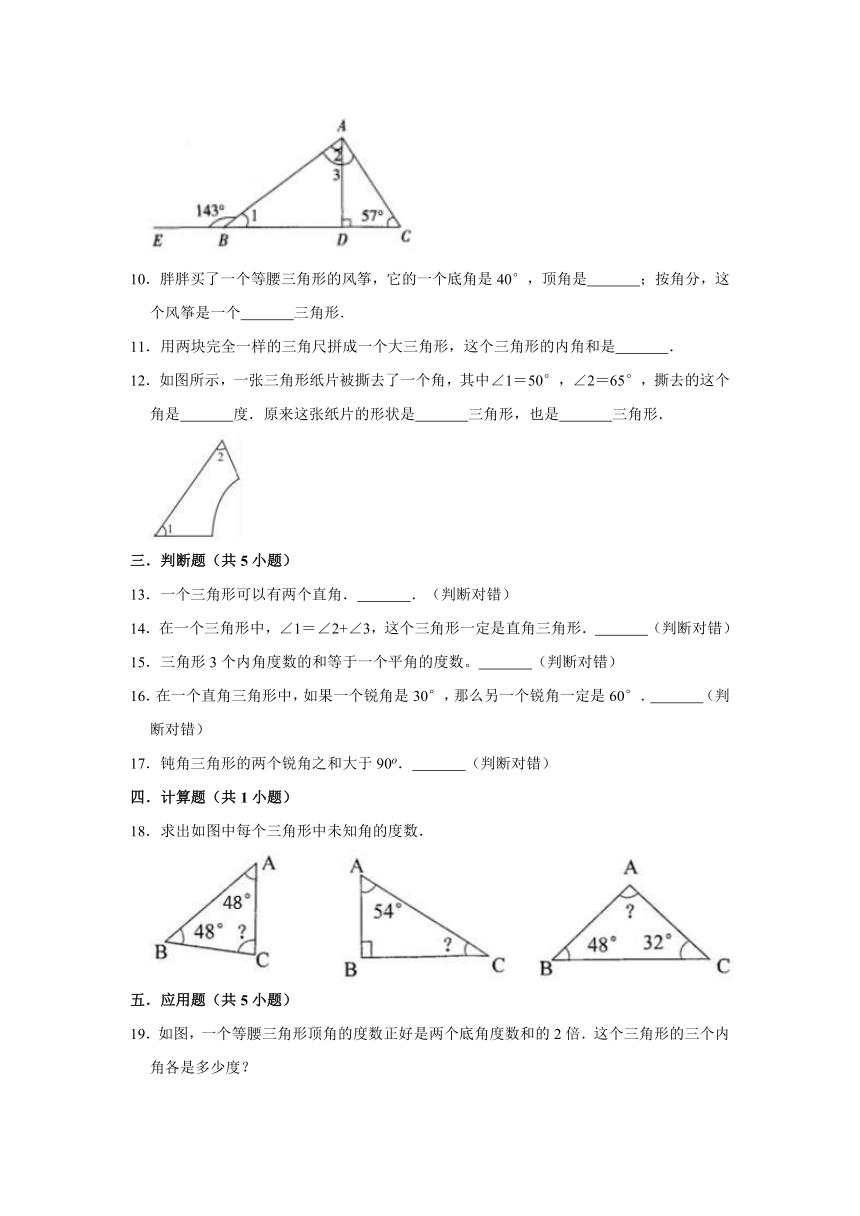
图片预览


文档简介
人教版小学四年级数学下册《第五章
三角形
5.3
三角形的内角和》同步测试题
一.选择题(共6小题)
1.一个三角形的内角和是( )度.
A.120
B.180
C.360
2.下列说法正确的是( )
A.角的两条边越长,角就越大
B.一个锐角三角形中任意两个角的和可能小于90°
C.一个三角形中至少有两个锐角
D.0.12和0.120的大小相等,计数单位也相同
3.把一个三角形分成两个小三角形,每个小三角形的内角和是( )
A.360°
B.90°
C.180°
4.一个钝角三角形的三个内角中,最多有( )个钝角.
A.1
B.2
C.3
5.把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是( )
A.45°和45°
B.30°和60°
C.45°和60°
6.一个等腰三角形的一个底角是25度,它的顶角是多少度?按角分类,这个三角形是什么三角形( )
A.77.5;
锐角三角形
B.90;直角三角形
C.130;
钝角三角形
二.填空题(共6小题)
7.在一个直角三角形中,一个锐角是75°,另一个锐角是
.
8.在一个三角形中,已知∠1=38°,∠2=52°,∠3=
,这是一个
三角形.
9.算一算,填一填.
(1)∠1=
°.
(2)∠2=
°.
(3)∠3=
°.
10.胖胖买了一个等腰三角形的风筝,它的一个底角是40°,顶角是
;按角分,这个风筝是一个
三角形.
11.用两块完全一样的三角尺拼成一个大三角形,这个三角形的内角和是
.
12.如图所示,一张三角形纸片被撕去了一个角,其中∠1=50°,∠2=65°,撕去的这个角是
度.原来这张纸片的形状是
三角形,也是
三角形.
三.判断题(共5小题)
13.一个三角形可以有两个直角.
.(判断对错)
14.在一个三角形中,∠1=∠2+∠3,这个三角形一定是直角三角形.
(判断对错)
15.三角形3个内角度数的和等于一个平角的度数。
(判断对错)
16.在一个直角三角形中,如果一个锐角是30°,那么另一个锐角一定是60°.
(判断对错)
17.钝角三角形的两个锐角之和大于90o.
(判断对错)
四.计算题(共1小题)
18.求出如图中每个三角形中未知角的度数.
五.应用题(共5小题)
19.如图,一个等腰三角形顶角的度数正好是两个底角度数和的2倍.这个三角形的三个内角各是多少度?
20.下面是三块三角形纸板的一部分,你知道它们原来各是什么三角形吗?(填一填)
21.如图,将直角三角形ABC的直角边BC延长到点D.已知∠1=58°,求∠2和∠3分别是多少度?
22.已知等腰三角形的一个内角是72°,它的另外有两个内角分别是多少度?
23.如图,黄霏霏同学不小心把一块三角形的玻璃打碎了,你能根据其中的一个碎片画出这块三角形玻璃吗?它是几号碎片?
六.解答题(共2小题)
24.一个等腰三角形的顶角是100°,它的底角是多少度?
25.一个直角三角形中,直角与一个锐角的和是138°,求这个锐角的度数是多少?
参考答案与试题解析
一.选择题(共6小题)
1.解:一个三角形的内角和是180度。
故选:B。
2.解:说法正确的是一个三角形中至少有两个锐角。
故选:C。
3.解:根据三角形的内角和是180度,所以把一个三角形分成两个三角形后,每个三角形的内角和都是180°。
故选:C。
4.解:假设钝角三角形中不只1个钝角,则根据钝角的意义可知,三角形的三个内角的和大于180°,与三角形内角和定理矛盾,所以一个钝角三角形的三个内角中,最多有1个钝角。
故选:A。
5.解:把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是30°和60°。
故选:B。
6.解:180﹣25×2
=180﹣50
=130(度)
答:它的顶角是130度,这个三角形是钝角三角形.
故选:C.
二.填空题(共6小题)
7.解:90°﹣75°=15°
故答案为:15°.
8.解:180°﹣38°﹣52°
=142°﹣52°
=90°
所以,∠3=90°,这是一个直角三角形。
故答案为:90°,直角。
9.解:(1)因为∠ABE+∠1=180°,∠ABE=143°
所以∠1=180°﹣143°=37°;
(2)因为∠1+∠2+∠ADB=180°,∠1=37°,∠ADB=90°
所以∠2=180°﹣90°﹣37°=53°;
(3)因为∠1+∠2+∠C=180°,∠1=37°,∠C=57°
所以∠3=180°﹣57°﹣37°=86°.
故答案为:37,53,86.
10.解:180°﹣(40°+40°)
=180°﹣80°
=100°
因为100°>90°,
所以这个风筝是一个钝角三角形,
故答案为:100°,钝角.
11.解:两块完全一样的三角尺拼成一个大三角形,这个三角形的内角和等于180°.
故答案为:180°.
12.解:180°﹣50°﹣65°=65°
三个角都是锐角,所以这个三角形是锐角三角形;因为有两个角的度数相等,所以这个三角形属于等腰三角形。
故答案为:65、锐角、等腰。
三.判断题(共5小题)
13.解:假设三角形有2个直角,
则这个三角形内角和一定会大于180度,
所以假设不成立,
因此一个三角形可以有两个直角,是错误的.
故答案为:×.
14.解:根据三角形内角和定理:∠1+∠2+∠3=180°,
已知∠1=∠2+∠3,
∠1+∠1=180°
∠1=180°÷2=90°
所以这个三角形一定是直角三角形,原题说法正确.
故答案为:√.
15.解:因为三角形的内角和是180度,平角是180度,所以三角形3个内角度数的和等于一个平角的度数。
因此,三角形3个内角度数的和等于一个平角的度数。这种说法是正确的。
故答案为:√。
16.解:180°﹣90°=90°
90°﹣30°=60°
所以:在一个直角三角形中,如果一个锐角是30°,那么另一个锐角一定是60°;原题说法正确。
故答案为:√。
17.解:钝角三角形中,有一个是钝角即大于90°,
因为三角形内角和是180°,所以另外两个角的度数之和一定小于90°.
故答案为:×.
四.计算题(共1小题)
18.解:(1)180°﹣48°﹣48°=84°
(2)180°﹣90°﹣54°=36°
(3)180°﹣32°﹣48°=100°
五.应用题(共5小题)
19.解:180÷(2×2+2)
=180÷6
=30°
30×4=120°
答:这个三角形的三个内角各是30°,30°,120°。
20.解:(1)180﹣50﹣71=59(度),即三个角均为锐角,此三角形为锐角三角形.
(2)180﹣37﹣49=94(度),第三个角为钝角,即此三角形为钝角三角形.
(3)180﹣35﹣55=90(度),即第三个角是直角,此三角形为直角三角形.
故答案为:
21.解:∠2=180°﹣90°﹣58°=32°
∠3=180°﹣32°=148°
答:∠2=32°,∠3=148°.
22.解:若顶角是72°,则两个底角的度数为:
(180°﹣72°)÷2
=108°÷2
=54°
若一个底角是72°,则顶角的度数为:
180°﹣72°×2
=180°﹣144°
=36°
答:它的另外有两个内角分别是54°、54°或72°、36°.
23.解:能根据③号碎片,画出这个三角形.
六.解答题(共2小题)
24.解:(180°﹣100°)÷2
=80°÷2
=40°
答:它的底角是40度.
25.解:138°﹣90°=48°
答:这个锐角的度数是48度.
三角形
5.3
三角形的内角和》同步测试题
一.选择题(共6小题)
1.一个三角形的内角和是( )度.
A.120
B.180
C.360
2.下列说法正确的是( )
A.角的两条边越长,角就越大
B.一个锐角三角形中任意两个角的和可能小于90°
C.一个三角形中至少有两个锐角
D.0.12和0.120的大小相等,计数单位也相同
3.把一个三角形分成两个小三角形,每个小三角形的内角和是( )
A.360°
B.90°
C.180°
4.一个钝角三角形的三个内角中,最多有( )个钝角.
A.1
B.2
C.3
5.把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是( )
A.45°和45°
B.30°和60°
C.45°和60°
6.一个等腰三角形的一个底角是25度,它的顶角是多少度?按角分类,这个三角形是什么三角形( )
A.77.5;
锐角三角形
B.90;直角三角形
C.130;
钝角三角形
二.填空题(共6小题)
7.在一个直角三角形中,一个锐角是75°,另一个锐角是
.
8.在一个三角形中,已知∠1=38°,∠2=52°,∠3=
,这是一个
三角形.
9.算一算,填一填.
(1)∠1=
°.
(2)∠2=
°.
(3)∠3=
°.
10.胖胖买了一个等腰三角形的风筝,它的一个底角是40°,顶角是
;按角分,这个风筝是一个
三角形.
11.用两块完全一样的三角尺拼成一个大三角形,这个三角形的内角和是
.
12.如图所示,一张三角形纸片被撕去了一个角,其中∠1=50°,∠2=65°,撕去的这个角是
度.原来这张纸片的形状是
三角形,也是
三角形.
三.判断题(共5小题)
13.一个三角形可以有两个直角.
.(判断对错)
14.在一个三角形中,∠1=∠2+∠3,这个三角形一定是直角三角形.
(判断对错)
15.三角形3个内角度数的和等于一个平角的度数。
(判断对错)
16.在一个直角三角形中,如果一个锐角是30°,那么另一个锐角一定是60°.
(判断对错)
17.钝角三角形的两个锐角之和大于90o.
(判断对错)
四.计算题(共1小题)
18.求出如图中每个三角形中未知角的度数.
五.应用题(共5小题)
19.如图,一个等腰三角形顶角的度数正好是两个底角度数和的2倍.这个三角形的三个内角各是多少度?
20.下面是三块三角形纸板的一部分,你知道它们原来各是什么三角形吗?(填一填)
21.如图,将直角三角形ABC的直角边BC延长到点D.已知∠1=58°,求∠2和∠3分别是多少度?
22.已知等腰三角形的一个内角是72°,它的另外有两个内角分别是多少度?
23.如图,黄霏霏同学不小心把一块三角形的玻璃打碎了,你能根据其中的一个碎片画出这块三角形玻璃吗?它是几号碎片?
六.解答题(共2小题)
24.一个等腰三角形的顶角是100°,它的底角是多少度?
25.一个直角三角形中,直角与一个锐角的和是138°,求这个锐角的度数是多少?
参考答案与试题解析
一.选择题(共6小题)
1.解:一个三角形的内角和是180度。
故选:B。
2.解:说法正确的是一个三角形中至少有两个锐角。
故选:C。
3.解:根据三角形的内角和是180度,所以把一个三角形分成两个三角形后,每个三角形的内角和都是180°。
故选:C。
4.解:假设钝角三角形中不只1个钝角,则根据钝角的意义可知,三角形的三个内角的和大于180°,与三角形内角和定理矛盾,所以一个钝角三角形的三个内角中,最多有1个钝角。
故选:A。
5.解:把一个等边三角形沿一条高对折,分成两个三角形,其中一个三角形的两个锐角分别是30°和60°。
故选:B。
6.解:180﹣25×2
=180﹣50
=130(度)
答:它的顶角是130度,这个三角形是钝角三角形.
故选:C.
二.填空题(共6小题)
7.解:90°﹣75°=15°
故答案为:15°.
8.解:180°﹣38°﹣52°
=142°﹣52°
=90°
所以,∠3=90°,这是一个直角三角形。
故答案为:90°,直角。
9.解:(1)因为∠ABE+∠1=180°,∠ABE=143°
所以∠1=180°﹣143°=37°;
(2)因为∠1+∠2+∠ADB=180°,∠1=37°,∠ADB=90°
所以∠2=180°﹣90°﹣37°=53°;
(3)因为∠1+∠2+∠C=180°,∠1=37°,∠C=57°
所以∠3=180°﹣57°﹣37°=86°.
故答案为:37,53,86.
10.解:180°﹣(40°+40°)
=180°﹣80°
=100°
因为100°>90°,
所以这个风筝是一个钝角三角形,
故答案为:100°,钝角.
11.解:两块完全一样的三角尺拼成一个大三角形,这个三角形的内角和等于180°.
故答案为:180°.
12.解:180°﹣50°﹣65°=65°
三个角都是锐角,所以这个三角形是锐角三角形;因为有两个角的度数相等,所以这个三角形属于等腰三角形。
故答案为:65、锐角、等腰。
三.判断题(共5小题)
13.解:假设三角形有2个直角,
则这个三角形内角和一定会大于180度,
所以假设不成立,
因此一个三角形可以有两个直角,是错误的.
故答案为:×.
14.解:根据三角形内角和定理:∠1+∠2+∠3=180°,
已知∠1=∠2+∠3,
∠1+∠1=180°
∠1=180°÷2=90°
所以这个三角形一定是直角三角形,原题说法正确.
故答案为:√.
15.解:因为三角形的内角和是180度,平角是180度,所以三角形3个内角度数的和等于一个平角的度数。
因此,三角形3个内角度数的和等于一个平角的度数。这种说法是正确的。
故答案为:√。
16.解:180°﹣90°=90°
90°﹣30°=60°
所以:在一个直角三角形中,如果一个锐角是30°,那么另一个锐角一定是60°;原题说法正确。
故答案为:√。
17.解:钝角三角形中,有一个是钝角即大于90°,
因为三角形内角和是180°,所以另外两个角的度数之和一定小于90°.
故答案为:×.
四.计算题(共1小题)
18.解:(1)180°﹣48°﹣48°=84°
(2)180°﹣90°﹣54°=36°
(3)180°﹣32°﹣48°=100°
五.应用题(共5小题)
19.解:180÷(2×2+2)
=180÷6
=30°
30×4=120°
答:这个三角形的三个内角各是30°,30°,120°。
20.解:(1)180﹣50﹣71=59(度),即三个角均为锐角,此三角形为锐角三角形.
(2)180﹣37﹣49=94(度),第三个角为钝角,即此三角形为钝角三角形.
(3)180﹣35﹣55=90(度),即第三个角是直角,此三角形为直角三角形.
故答案为:
21.解:∠2=180°﹣90°﹣58°=32°
∠3=180°﹣32°=148°
答:∠2=32°,∠3=148°.
22.解:若顶角是72°,则两个底角的度数为:
(180°﹣72°)÷2
=108°÷2
=54°
若一个底角是72°,则顶角的度数为:
180°﹣72°×2
=180°﹣144°
=36°
答:它的另外有两个内角分别是54°、54°或72°、36°.
23.解:能根据③号碎片,画出这个三角形.
六.解答题(共2小题)
24.解:(180°﹣100°)÷2
=80°÷2
=40°
答:它的底角是40度.
25.解:138°﹣90°=48°
答:这个锐角的度数是48度.
