2020-2021学年 苏科版七年级数学下册第7章 平面图形的认识(二) 填空题易错题 练习(一)(word版含答案)
文档属性
| 名称 | 2020-2021学年 苏科版七年级数学下册第7章 平面图形的认识(二) 填空题易错题 练习(一)(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 22:35:39 | ||
图片预览




文档简介
七年级数学苏科版下册第7章《平面图形的认识(二)》
填空题易错题培优练习(一)
1.已知直线m∥n,将一块含有30°角的三角板ABC按如图所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=15°,则∠2=
°.
2.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,∠BOF=
度;
(2)若∠BOF=36°,∠AOC=
度.
3.如图,将△ABC水平向右平移至△DEF的位置,点B,E,C,F在同一直线上,已知BF=8,CE=2,则BE=
.
4.如图,直线AB∥CD,∠E为直角,则∠1=
.
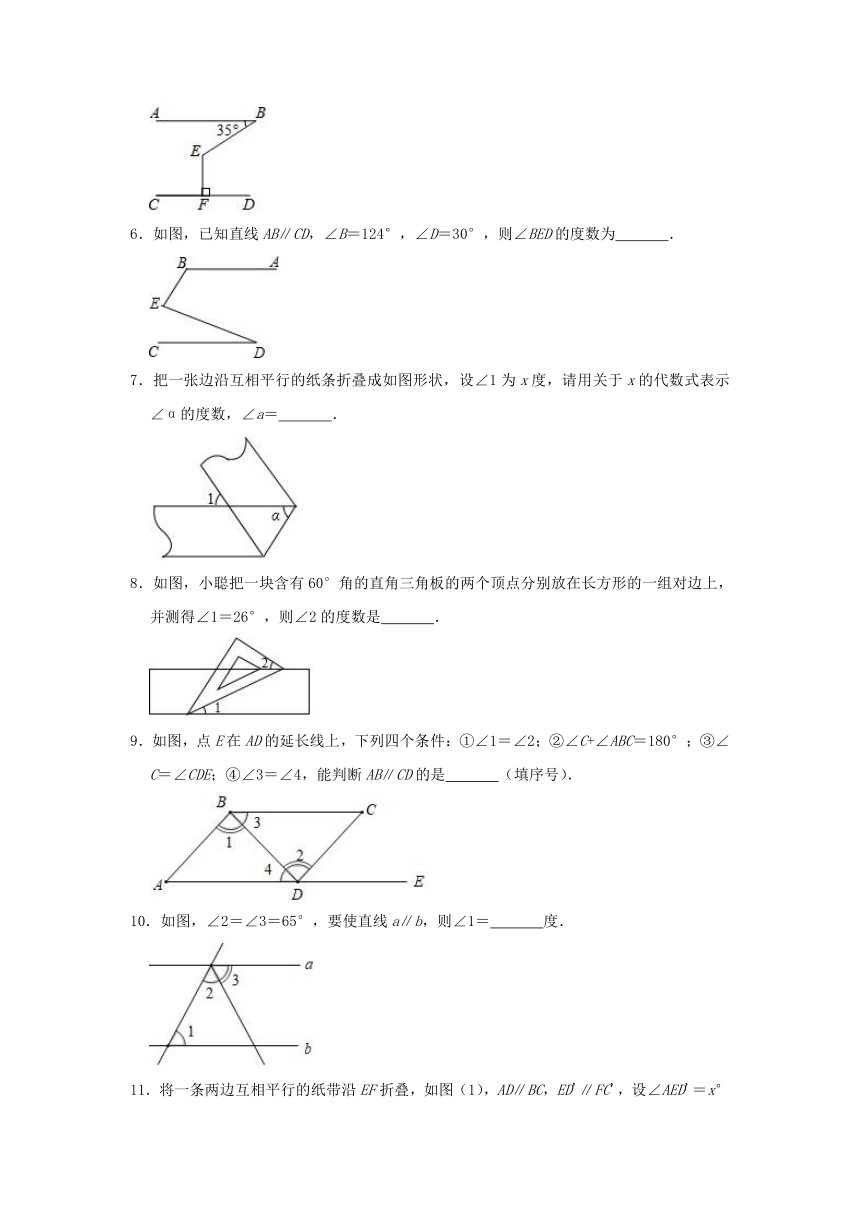
5.如图,AB∥CD,EF⊥CD于点F,若∠ABE=35°,则∠BEF=
.
6.如图,已知直线AB∥CD,∠B=124°,∠D=30°,则∠BED的度数为
.
7.把一张边沿互相平行的纸条折叠成如图形状,设∠1为x度,请用关于x的代数式表示∠α的度数,∠a=
.
8.如图,小聪把一块含有60°角的直角三角板的两个顶点分别放在长方形的一组对边上,并测得∠1=26°,则∠2的度数是
.
9.如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是
(填序号).
10.如图,∠2=∠3=65°,要使直线a∥b,则∠1=
度.
11.将一条两边互相平行的纸带沿EF折叠,如图(1),AD∥BC,ED'∥FC',设∠AED'=x°
(1)∠EFB=
.(用含x的代数式表示)
(2)若将图1继续沿BF折叠成图(2),∠EFC″=
.(用含x的代数式表示).
12.如图,已知直线a∥b,小敏把三角板的直角顶点放在直线b上,若∠1=40°,则∠2的度数是
.
13.已知:直线a∥b,点A,B分别是a,b上的点,APB是a,b之间的一条折线段,且50°<∠APB<90°,Q是a,b之间且在折线段APB左侧的一点,如图.若∠AQC的一边与PA的夹角为40°,另一边与PB平行,请直接写出∠AQC,∠1,∠2之间满足的数量关系是
.
14.如图,直线a∥b,直角角板的直角顶点C在直线b上,若∠1=32°,则∠2=
.
15.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上,设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④﹣β,⑤360°﹣α﹣β,可以表示∠AEC度数的是
(请填写正确答案的序号)
16.如图,已知∠1=∠2,∠B=35°,则∠3=
.
17.如图所示的长方形纸条ABCD,将纸片沿MN折叠,MB与DN交于点K,若∠1=70°,则∠MKN=
°.
18.如图,在△ABC中,∠BAC=35°,延长AB到点D,∠CBD=65°,过顶点A作AE∥BC,则∠CAE=
°.
19.已知AB∥CD,AE、CE分别平分∠FAB、∠FCD,∠E=15°,则∠F=
°.
20.若∠1和∠2是对顶角,∠1=35°,则∠2的补角是
.
参考答案
1.解:∵m∥n,
∴∠2=∠ABC+∠1=30°+15°=45°.
故答案为:45.
2.解:(1)∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC=76°,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB=38°,
∴∠COE=180°﹣∠DOE=142°,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE=71°,
∴∠BOF=∠FOE﹣∠EOB=33°.
故答案为33°.
(2))∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE,
∵∠AOC=180°﹣∠COF﹣∠BOF
=180°﹣(∠EOB+∠BOF)﹣∠BOF
=108°﹣∠EOB
=108°﹣∠AOC
∴∠AOC=72°.
故答案为72°.
3.解:∵△ABC向右平移后得到△DEF,
BF=8,CE=2,
∴BE+CF=8﹣2=6,
∵BE=CF,
∴BE=3,
故答案为:3.
4.解:如图,过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠C=∠FEC,∠BAE=∠FEA,
∵∠C=44°,∠AEC为直角,
∴∠FEC=44°,∠BAE=∠AEF=90°﹣44°=46°,
∴∠1=180°﹣∠BAE=180°﹣46°=134°,
故答案为:134°.
5.解:如图,过点E作GH∥AB.则∠ABE=∠BEH=35°.
∵AB∥CD,
∴GH∥CD.
又∵EF⊥CD,
∴EF⊥GH,
∴∠BEF=∠BEH+∠HEF=35°+90°=125°
故答案为:125°.
6.解:过点E作EF∥AB,
∵∠B=124°,
∴∠BEF=180°﹣124°=56°.
∵AB∥CD,∠D=30°,
∴EF∥CD,
∴∠D=∠DEF=30°,
∴∠BED=∠BEF+∠DEF=56°+30°=86°.
故答案为:86°.
7.解:∵AB∥CD,
∴∠2=∠1=x°,∠3=∠α,
∵将一条上下两边互相平行的纸带折叠,
∴∠3=∠4=(180°﹣∠2)=90°﹣∠2=90°﹣x°,
∴∠α=∠3=90°﹣x°.
故答案为:90°﹣x°.
8.解:∵直尺的两边互相平行,∠1=26°,
∴∠3=∠1=26°,
∴∠2=60°﹣∠3=60°﹣26°=34°.
故答案为34°.
9.解:①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
10.解:要使直线a∥b,必须∠1+∠2+∠3=180°,
∴∠1=180°﹣65°﹣65°=50°,
故答案为50.
11.解:(1)如图1所示:
∵AD∥BC,
∴∠DEF=∠EFB,∠AEH+∠EHB=180°,
又∵∠DEF=∠D'EF,
∴∠D'EF=∠EFB,
又∵∠EHB=∠D'EF+∠EFB,
∴∠EFB=∠EHB,
又∵∠AED'=x°,
∴∠EHB=180°﹣x°
∴∠EFB==90°﹣x°
(2)如图2所示:
∵∠EFB+∠EFC'=180°,
∴∠EFC'=180°﹣(90°﹣°)=90°+,
又∵∠EFC'=2∠EFB+∠EFC'',
∴∠EFC''=∠EFC'﹣2∠EFB
=90°+﹣2(90°﹣°)
=,
故答案为.
12.解:∵∠1+∠3=90°,
∴∠3=90°﹣40°=50°,
∵a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故答案为130°.
13.解:①作QC∥BP交AP于点C,PD∥a,连接AQ,
如图1所示:
∵PD∥a,b∥a,
∴PD∥b,
∴∠2=∠BPD,
又∵PD∥a,
∴∠1=∠APD,
又∵∠APB=∠APD+∠BPD,
∴∠APB=∠1+∠2,
又∵QC∥PD,
∴∠APB=∠ACQ,
∴∠ACQ=∠1+∠2,
又∵∠AQC+∠ACQ+∠QAC=180°,
∠QAC=40°,
∴∠AQC+∠ACQ=140°,
∴∠AQC+∠1+∠2=140°;
②作QC∥BP交AP于点D,直线b于点C,PH∥a,连接AQ,
如图2所示:
同理可得:∠ADQ=∠1+∠2,
∵∠AQC=∠QAP+∠ADQ,
∠QAP=40°,
∴∠AQC﹣∠1﹣∠2=40°.
综合所述:∠AQC,∠1,∠2之间满足的数量关系:
∠AQC+∠1+∠2=140°或∠AQC﹣∠1﹣∠2=40°.
14.解:如图所示:
∵a∥b,
∴∠1=∠3,∠2=∠4,
又∵∠1=32°,
∴∠3=32°,
又∵∠3+∠ABC+∠4=180°,
∠ABC=90°,
∴∠3+∠4=90°,
∴∠4=58°,
∴∠2=58°.
故答案为58°.
15.解:(1)如图1,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β﹣α.
(2)如图2,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)如图3,由AB∥CD,可得∠BOE3=∠DCE3=β,
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α﹣β.
(4)如图4,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°﹣α﹣β.
(5)(6)当点E在CD的下方时,同理可得,∠AEC=α﹣β或β﹣α.
综上所述,∠AEC的度数可能为β﹣α,α+β,α﹣β,360°﹣α﹣β.
故答案为:①②③⑤.
16.解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠B,
∵∠B=35°,
∴∠3=35°.
故答案为35°.
17.解:由折叠的性质可得:∠1=∠KMN=70°,
∴∠KMA=180°﹣70°﹣70°=40°,
∵DN∥AM,
∴∠MKN=∠KMA=40°,
故答案为:40
18.解:∵AE∥BC,
∴∠CBD=∠EAB=65°,
∴∠CAE=∠EAB﹣∠BAC=65°﹣35°
=30°.
故答案为:30.
19.解:延长EA交CD于G,如图所示:
∵AB∥CD,
∴∠AGD=∠EAB,
∵AE、CE分别平分∠FAB、∠FCD,
∴∠EAF=∠EAB=∠AGD,∠ECF=∠ECD,
∵∠AGD=∠ECD+∠E,
∴∠EAF=∠ECF+∠E,
∵∠CHF=∠AHE,
∴∠F+∠ECF=∠EAF+∠E,
即∠F+∠ECF=∠ECF+∠E+∠E,
∴∠F=2∠E=30°;
故答案为:30.
20.解:∵∠1与∠2是对顶角,
∴∠1=∠2,
又∵∠2与∠3是补角,
∴∠2+∠3=180°,
等角代换得∠1+∠3=180°
∴∠3=180°﹣35°=145°,
故答案为:145°.
填空题易错题培优练习(一)
1.已知直线m∥n,将一块含有30°角的三角板ABC按如图所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=15°,则∠2=
°.
2.如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,∠BOF=
度;
(2)若∠BOF=36°,∠AOC=
度.
3.如图,将△ABC水平向右平移至△DEF的位置,点B,E,C,F在同一直线上,已知BF=8,CE=2,则BE=
.
4.如图,直线AB∥CD,∠E为直角,则∠1=
.
5.如图,AB∥CD,EF⊥CD于点F,若∠ABE=35°,则∠BEF=
.
6.如图,已知直线AB∥CD,∠B=124°,∠D=30°,则∠BED的度数为
.
7.把一张边沿互相平行的纸条折叠成如图形状,设∠1为x度,请用关于x的代数式表示∠α的度数,∠a=
.
8.如图,小聪把一块含有60°角的直角三角板的两个顶点分别放在长方形的一组对边上,并测得∠1=26°,则∠2的度数是
.
9.如图,点E在AD的延长线上,下列四个条件:①∠1=∠2;②∠C+∠ABC=180°;③∠C=∠CDE;④∠3=∠4,能判断AB∥CD的是
(填序号).
10.如图,∠2=∠3=65°,要使直线a∥b,则∠1=
度.
11.将一条两边互相平行的纸带沿EF折叠,如图(1),AD∥BC,ED'∥FC',设∠AED'=x°
(1)∠EFB=
.(用含x的代数式表示)
(2)若将图1继续沿BF折叠成图(2),∠EFC″=
.(用含x的代数式表示).
12.如图,已知直线a∥b,小敏把三角板的直角顶点放在直线b上,若∠1=40°,则∠2的度数是
.
13.已知:直线a∥b,点A,B分别是a,b上的点,APB是a,b之间的一条折线段,且50°<∠APB<90°,Q是a,b之间且在折线段APB左侧的一点,如图.若∠AQC的一边与PA的夹角为40°,另一边与PB平行,请直接写出∠AQC,∠1,∠2之间满足的数量关系是
.
14.如图,直线a∥b,直角角板的直角顶点C在直线b上,若∠1=32°,则∠2=
.
15.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上,设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④﹣β,⑤360°﹣α﹣β,可以表示∠AEC度数的是
(请填写正确答案的序号)
16.如图,已知∠1=∠2,∠B=35°,则∠3=
.
17.如图所示的长方形纸条ABCD,将纸片沿MN折叠,MB与DN交于点K,若∠1=70°,则∠MKN=
°.
18.如图,在△ABC中,∠BAC=35°,延长AB到点D,∠CBD=65°,过顶点A作AE∥BC,则∠CAE=
°.
19.已知AB∥CD,AE、CE分别平分∠FAB、∠FCD,∠E=15°,则∠F=
°.
20.若∠1和∠2是对顶角,∠1=35°,则∠2的补角是
.
参考答案
1.解:∵m∥n,
∴∠2=∠ABC+∠1=30°+15°=45°.
故答案为:45.
2.解:(1)∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC=76°,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB=38°,
∴∠COE=180°﹣∠DOE=142°,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE=71°,
∴∠BOF=∠FOE﹣∠EOB=33°.
故答案为33°.
(2))∵∠DOB和∠AOC是对顶角,
∴∠DOB=∠AOC,
∵OE平分∠BOD,
∴∠DOE=∠EOB=∠DOB,
∵OF平分∠COE,
∴∠COF=∠FOE=∠COE,
∵∠AOC=180°﹣∠COF﹣∠BOF
=180°﹣(∠EOB+∠BOF)﹣∠BOF
=108°﹣∠EOB
=108°﹣∠AOC
∴∠AOC=72°.
故答案为72°.
3.解:∵△ABC向右平移后得到△DEF,
BF=8,CE=2,
∴BE+CF=8﹣2=6,
∵BE=CF,
∴BE=3,
故答案为:3.
4.解:如图,过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠C=∠FEC,∠BAE=∠FEA,
∵∠C=44°,∠AEC为直角,
∴∠FEC=44°,∠BAE=∠AEF=90°﹣44°=46°,
∴∠1=180°﹣∠BAE=180°﹣46°=134°,
故答案为:134°.
5.解:如图,过点E作GH∥AB.则∠ABE=∠BEH=35°.
∵AB∥CD,
∴GH∥CD.
又∵EF⊥CD,
∴EF⊥GH,
∴∠BEF=∠BEH+∠HEF=35°+90°=125°
故答案为:125°.
6.解:过点E作EF∥AB,
∵∠B=124°,
∴∠BEF=180°﹣124°=56°.
∵AB∥CD,∠D=30°,
∴EF∥CD,
∴∠D=∠DEF=30°,
∴∠BED=∠BEF+∠DEF=56°+30°=86°.
故答案为:86°.
7.解:∵AB∥CD,
∴∠2=∠1=x°,∠3=∠α,
∵将一条上下两边互相平行的纸带折叠,
∴∠3=∠4=(180°﹣∠2)=90°﹣∠2=90°﹣x°,
∴∠α=∠3=90°﹣x°.
故答案为:90°﹣x°.
8.解:∵直尺的两边互相平行,∠1=26°,
∴∠3=∠1=26°,
∴∠2=60°﹣∠3=60°﹣26°=34°.
故答案为34°.
9.解:①由∠1=∠2,可以判定AB∥CD.
②由∠C+∠ABC=180°,可以判定AB∥CD.
③由∠C=∠CDE,可以判定BC∥AD.
④由∠3=∠4,可以判定BC∥AD.
故答案为①②.
10.解:要使直线a∥b,必须∠1+∠2+∠3=180°,
∴∠1=180°﹣65°﹣65°=50°,
故答案为50.
11.解:(1)如图1所示:
∵AD∥BC,
∴∠DEF=∠EFB,∠AEH+∠EHB=180°,
又∵∠DEF=∠D'EF,
∴∠D'EF=∠EFB,
又∵∠EHB=∠D'EF+∠EFB,
∴∠EFB=∠EHB,
又∵∠AED'=x°,
∴∠EHB=180°﹣x°
∴∠EFB==90°﹣x°
(2)如图2所示:
∵∠EFB+∠EFC'=180°,
∴∠EFC'=180°﹣(90°﹣°)=90°+,
又∵∠EFC'=2∠EFB+∠EFC'',
∴∠EFC''=∠EFC'﹣2∠EFB
=90°+﹣2(90°﹣°)
=,
故答案为.
12.解:∵∠1+∠3=90°,
∴∠3=90°﹣40°=50°,
∵a∥b,
∴∠2+∠3=180°.
∴∠2=180°﹣50°=130°.
故答案为130°.
13.解:①作QC∥BP交AP于点C,PD∥a,连接AQ,
如图1所示:
∵PD∥a,b∥a,
∴PD∥b,
∴∠2=∠BPD,
又∵PD∥a,
∴∠1=∠APD,
又∵∠APB=∠APD+∠BPD,
∴∠APB=∠1+∠2,
又∵QC∥PD,
∴∠APB=∠ACQ,
∴∠ACQ=∠1+∠2,
又∵∠AQC+∠ACQ+∠QAC=180°,
∠QAC=40°,
∴∠AQC+∠ACQ=140°,
∴∠AQC+∠1+∠2=140°;
②作QC∥BP交AP于点D,直线b于点C,PH∥a,连接AQ,
如图2所示:
同理可得:∠ADQ=∠1+∠2,
∵∠AQC=∠QAP+∠ADQ,
∠QAP=40°,
∴∠AQC﹣∠1﹣∠2=40°.
综合所述:∠AQC,∠1,∠2之间满足的数量关系:
∠AQC+∠1+∠2=140°或∠AQC﹣∠1﹣∠2=40°.
14.解:如图所示:
∵a∥b,
∴∠1=∠3,∠2=∠4,
又∵∠1=32°,
∴∠3=32°,
又∵∠3+∠ABC+∠4=180°,
∠ABC=90°,
∴∠3+∠4=90°,
∴∠4=58°,
∴∠2=58°.
故答案为58°.
15.解:(1)如图1,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β﹣α.
(2)如图2,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)如图3,由AB∥CD,可得∠BOE3=∠DCE3=β,
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α﹣β.
(4)如图4,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°﹣α﹣β.
(5)(6)当点E在CD的下方时,同理可得,∠AEC=α﹣β或β﹣α.
综上所述,∠AEC的度数可能为β﹣α,α+β,α﹣β,360°﹣α﹣β.
故答案为:①②③⑤.
16.解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠B,
∵∠B=35°,
∴∠3=35°.
故答案为35°.
17.解:由折叠的性质可得:∠1=∠KMN=70°,
∴∠KMA=180°﹣70°﹣70°=40°,
∵DN∥AM,
∴∠MKN=∠KMA=40°,
故答案为:40
18.解:∵AE∥BC,
∴∠CBD=∠EAB=65°,
∴∠CAE=∠EAB﹣∠BAC=65°﹣35°
=30°.
故答案为:30.
19.解:延长EA交CD于G,如图所示:
∵AB∥CD,
∴∠AGD=∠EAB,
∵AE、CE分别平分∠FAB、∠FCD,
∴∠EAF=∠EAB=∠AGD,∠ECF=∠ECD,
∵∠AGD=∠ECD+∠E,
∴∠EAF=∠ECF+∠E,
∵∠CHF=∠AHE,
∴∠F+∠ECF=∠EAF+∠E,
即∠F+∠ECF=∠ECF+∠E+∠E,
∴∠F=2∠E=30°;
故答案为:30.
20.解:∵∠1与∠2是对顶角,
∴∠1=∠2,
又∵∠2与∠3是补角,
∴∠2+∠3=180°,
等角代换得∠1+∠3=180°
∴∠3=180°﹣35°=145°,
故答案为:145°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
