2020-2021学年 苏科版七年级数学下册第7章 平面图形的认识(二) 填空题易错题 练习(二)(word版含答案)
文档属性
| 名称 | 2020-2021学年 苏科版七年级数学下册第7章 平面图形的认识(二) 填空题易错题 练习(二)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 183.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 22:37:26 | ||
图片预览


文档简介
七年级数学苏科版下册第7章《平面图形的认识(二)》
填空题易错题培优练习(二)
1.如图是我校徽标抽象的几何图形,若AB∥CD,∠FED=65°,则∠B+∠F+∠FED+∠D=
°.
2.学行线的相关知识后,学霸君轩轩利用如图所示的方法,可以折出“过已知直线外一点和已知直线平行”的直线.由操作过程可知他折平行线的依据可以是
.(把所有正确结论的序号都填在横线上)
①平行于同一条直线的两条直线平行;②同位角相等,两直线平行;③内错角相等,两直线平行;④同旁内角互补,两直线平行.
3.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=56°23′,则∠BOC的度数为
.
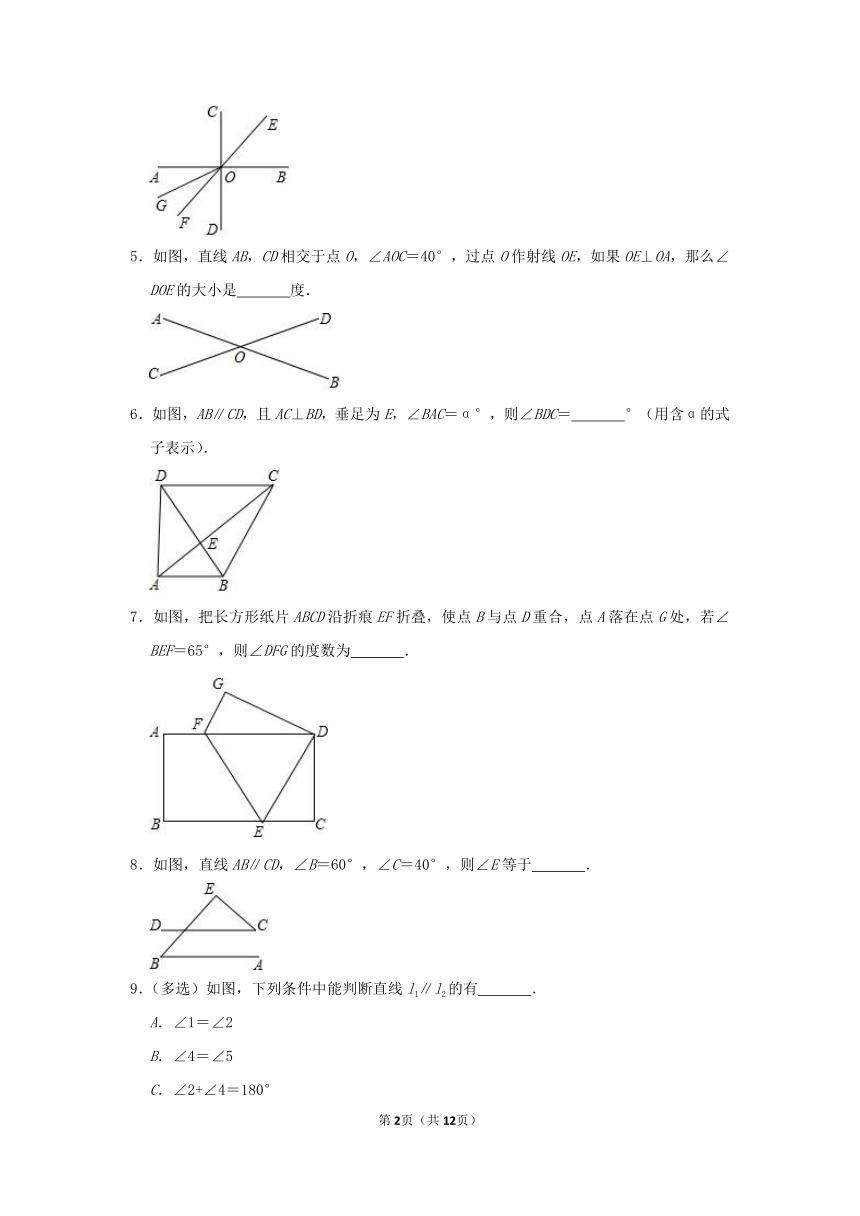
4.如图,∠BOE的对顶角是
.
5.如图,直线AB,CD相交于点O,∠AOC=40°,过点O作射线OE,如果OE⊥OA,那么∠DOE的大小是
度.
6.如图,AB∥CD,且AC⊥BD,垂足为E,∠BAC=α°,则∠BDC=
°(用含α的式子表示).
7.如图,把长方形纸片ABCD沿折痕EF折叠,使点B与点D重合,点A落在点G处,若∠BEF=65°,则∠DFG的度数为
.
8.如图,直线AB∥CD,∠B=60°,∠C=40°,则∠E等于
.
9.(多选)如图,下列条件中能判断直线l1∥l2的有
.
A.∠1=∠2
B.∠4=∠5
C.∠2+∠4=180°
D.∠1=∠3
E.∠6=∠1+∠2
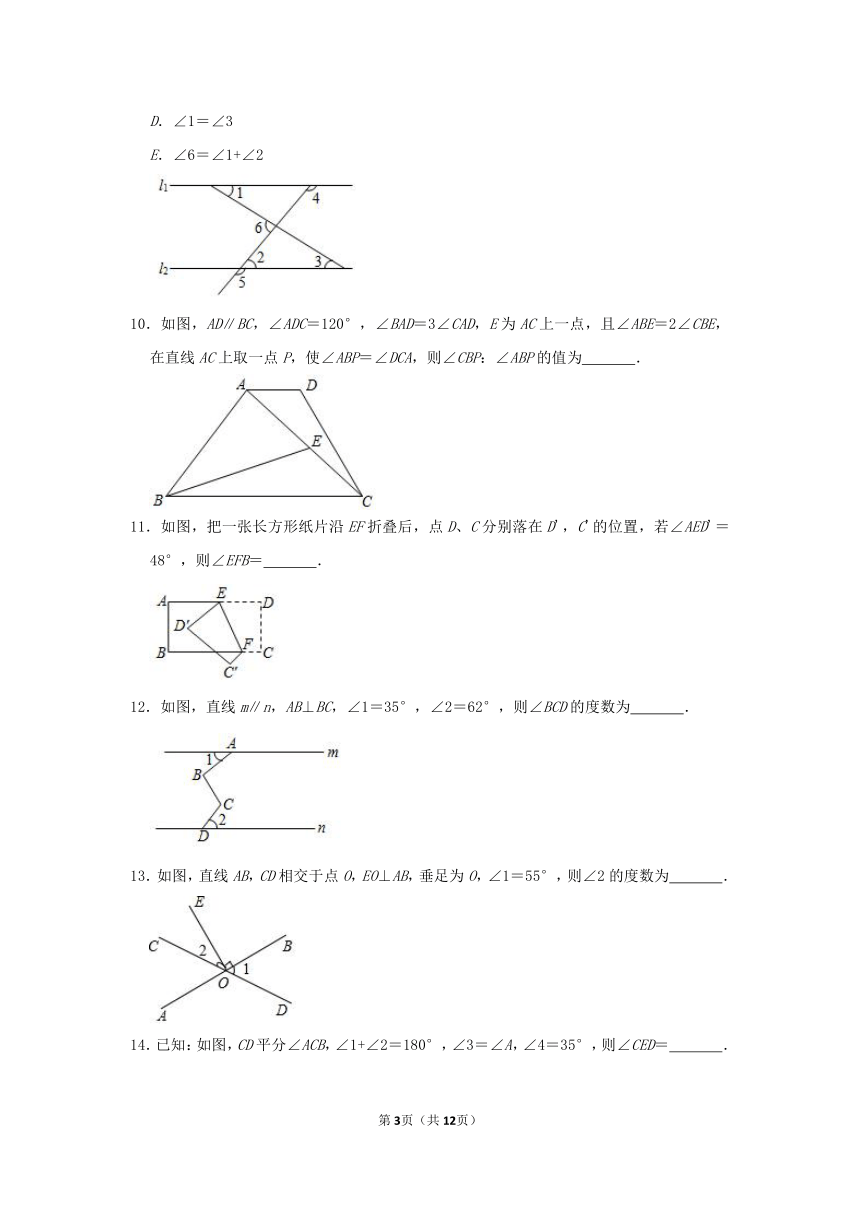
10.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为
.
11.如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D',C'的位置,若∠AED'=48°,则∠EFB=
.
12.如图,直线m∥n,AB⊥BC,∠1=35°,∠2=62°,则∠BCD的度数为
.
13.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠1=55°,则∠2的度数为
.
14.已知:如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=
.
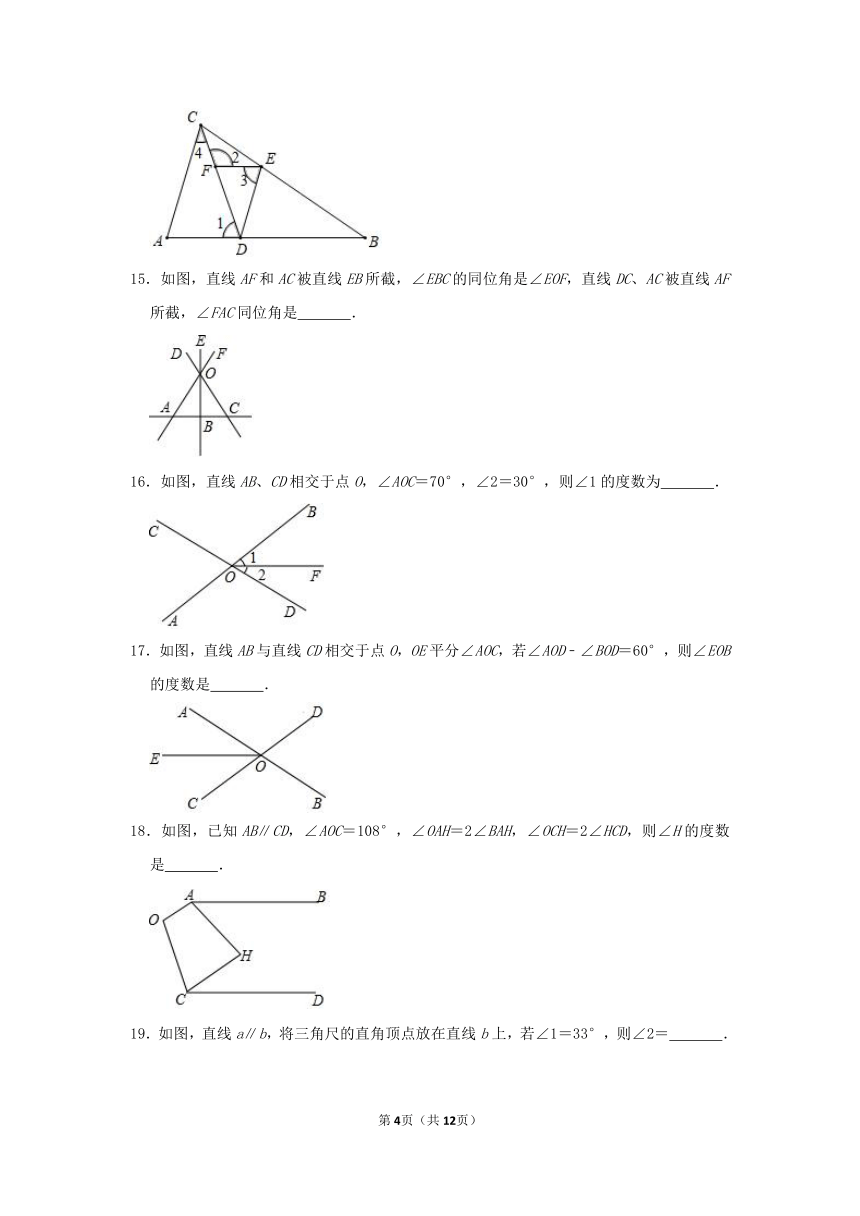
15.如图,直线AF和AC被直线EB所截,∠EBC的同位角是∠EOF,直线DC、AC被直线AF所截,∠FAC同位角是
.
16.如图,直线AB、CD相交于点O,∠AOC=70°,∠2=30°,则∠1的度数为
.
17.如图,直线AB与直线CD相交于点O,OE平分∠AOC,若∠AOD﹣∠BOD=60°,则∠EOB的度数是
.
18.如图,已知AB∥CD,∠AOC=108°,∠OAH=2∠BAH,∠OCH=2∠HCD,则∠H的度数是
.
19.如图,直线a∥b,将三角尺的直角顶点放在直线b上,若∠1=33°,则∠2=
.
20.把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MM,∠1=100°,则∠2的度数为
.
参考答案
1.解:如图所示,过F作FG∥AB,过E作EH∥CD,
∵AB∥CD,
∴EH∥CD∥AB∥CD,
∴∠B+∠BFG=180°,∠GFE=∠FEH,∠CDE=∠DEH,
∵∠DEF=65°,
∴∠GFE+∠CDE=∠FEH+∠DEH=∠FED=65°,
∴∠B+∠BFE+∠FED+∠D=180°+65°×2=310°,
故答案为:310.
2.解:如图,由题图(2)的操作可知PE⊥CD,所以∠PEC=∠PED=90°.由题图(3)的操作可知AB⊥PE,所以∠APE=∠BPE=90°,所以∠PEC=∠PED=∠APE=∠BPE=90°,所以可依据结论②,③或④判定AB∥CD,
故答案为②③④.
3.解:∵EO⊥AB于点O,∠EOD=56°23′,
∴∠BOD=90°﹣56°23′=33°37′,
∴∠BOC的度数为:180°﹣33°37′=146°23′.
故答案为:146°23′.
4.解:如图,∠BOE的对顶角是∠AOF.
故答案是:∠AOF.
5.解:如图所示,
当OE在直线CD上方时,
∵直线AB与直线CD相交,∠AOC=40°,
∴∠BOD=∠AOC=40°.
∵EO⊥AB,
∴∠BOE=90°,
∴∠DOE=∠BOE﹣∠BOD=90°﹣40°=50°;
当OE在OB与OC之间时,
∵∠BOE=90°,
∴∠DOE=∠BOE+∠BOD=90°+40°=130°.
故答案为:50或130
6.解:∵AC⊥BD,∠BAC=α°,
∴∠ABE=90°﹣α°,
又∵AB∥CD,
∴∠BDC=∠ABE=90°﹣α°,
故答案为:(90﹣α).
7.解:∵四边形ABCD是矩形,
∴AD∥BC,
∵∠BEF=65°,
∴∠DFE=∠BEF=65°,∠AFE=180°﹣∠BEF=115°,
由折叠的性质知∠GFE=∠AFE=115°,
则∠DFG=∠GFE﹣∠DFE=50°,
故答案为:50°.
8.解:如图所示:
∵AB∥CD,
∴∠B=∠EFC,
又∵∠B=60°,
∴∠EFC=60°,
又∵∠C+∠E+∠EFC=180°,
∠C=40°,
∴∠E=180°﹣∠C﹣∠EFC
=180°﹣40°﹣60°
=80°
故答案为80°.
9.解:A、∠1和∠2不是直线l1、l2被第三条直线所截形成的角,故不能判断直线l1∥l2.
B、∵∠4=∠5,∴l1∥l2(同位角相等两直线平行).
C、∠2、∠4是直线l1、l2被第三条直线所截形成的同旁内角,故∠2+∠4=180°能判断直线l1∥l2.
D、∵∠1=∠3,∴l1∥l2(内错角相等两直线平行).
E、作l1∥l,∴∠1=∠7,∵∠6=∠7+∠8,∴∠8=∠2,∴l∥l2,∴l1∥l2.
故答案为:BCDE.
10.解:如图,①当∠ABP1=∠DCA时,即∠1=∠2,
∵∠D=120°,
∴∠1+∠3=180°﹣120°=60°,
∵∠BAD=3∠CAD,∠ABE=2∠CBE,AD∥BC,
∴3∠3+3∠EBC=180°,
∴∠3+∠EBC=60°,
∴∠EBC=∠1=∠2=∠P1BE,
∴∠CBP1:∠ABP1的值为2,
②当∠ABP2=∠DCA时,∴∠CBP2:∠ABP2的值为4,
故答案为:2或4.
11.解:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DEF=∠EFB,
又由折叠的性质可得∠D′EF=∠DEF,
∵∠AED′+∠D′EF+∠DEF=180°,∠AED′=50°,
∠D′EF=∠DEF==66°,
∴∠EFB=∠DEF=66°.
故答案为:66°.
12.解:如图,过B作BE∥m,过C作CF∥n,
∵m∥n,
∴m∥BE∥CF∥n,
∴∠ABE=∠1=35°,∠DCF=∠2=62°,
又∵AB⊥BC,
∴∠ABC=90°,
∴∠EBC=90°﹣35°=55°,
∴∠BCF=∠EBC=55°,
∴∠BCD=∠BCF+∠DCF=55°+62°=117°.
故答案为:117°.
13.解:∵EO⊥AB,
∴∠EOB=90°,
∵∠1=55°,
∴∠2=180°﹣90°﹣55°=35°.
故答案为:35°.
14.解:∵∠1+∠2=180°,∠1+∠BDC=180°
∴∠2=∠BDC
∴EF∥AB
∴∠3=∠BDE
∵∠3=∠A
∴∠A=∠BDE
∴AC∥DE
∴∠ACB+∠CED=180°
∵CD平分∠ACB,∠4=35°
∴∠ACB=2∠4=2×35°=70°
∴∠CED=180°﹣∠ACB=180°﹣70°=110°
故答案为:110°.
15.解:根据同位角的图形特点,可得∠FAC的同位角是∠COF,
故答案为∠COF.
16.解:∵∠AOC=∠BOD=70°,∠2=30°,
∴∠1=∠BOD﹣∠2=70°﹣30°=40°,
故答案为:40°.
17.解:∵∠AOD+∠DOB=180°,∠AOD﹣∠DOB=60°,
∴∠AOD=120°,∠DOB=60°,
∴∠AOC=∠DOB=60°,∠BOC=∠AOD=120°,
∵OE平分∠AOC,
∴∠EOC=∠AOC=30°,
∴∠EOB=∠EOC+∠BOC=150°.
故答案为:150°.
18.解:过点O作OE∥AB,过点H作HF∥AB,则AB∥OE∥HF∥CD,
∴∠BAO+∠AOE=∠OCD+∠EOC=180°,
∵∠AOC=∠AOE+EOC=108°,
∴∠BAO+∠OCD=180°+180°﹣108°=252°,
∵∠OAH=2∠BAH,∠OCH=2∠DCH,
∴∠BAH+∠DCH=(∠BAO+∠OCD)=84°,
∵AB∥HF∥CD,
∴∠BAH=∠AHF,∠DCH=∠CHF,
∴∠AHC=∠AHF+∠CHF=∠BAH+∠DCH=84°,
故答案为:84°.
19.解:∵∠1+90°+∠3=180°,∠1=33°,
∴∠3=57°.
∵直线a∥b,
∴∠2=∠3=57°.
故答案为:57°.
20.解:∵EF∥MM,
∴∠3=∠1=100°.
∵∠3+∠4=180°,
∴∠4=180°﹣100°=80°.
∵∠4=∠5+∠ABC,∠ABC=30°,
∴∠5=80°﹣30°=50°,
∴∠2=180°﹣50°=130°.
故答案为:130°.
第1页(共1页)
填空题易错题培优练习(二)
1.如图是我校徽标抽象的几何图形,若AB∥CD,∠FED=65°,则∠B+∠F+∠FED+∠D=
°.
2.学行线的相关知识后,学霸君轩轩利用如图所示的方法,可以折出“过已知直线外一点和已知直线平行”的直线.由操作过程可知他折平行线的依据可以是
.(把所有正确结论的序号都填在横线上)
①平行于同一条直线的两条直线平行;②同位角相等,两直线平行;③内错角相等,两直线平行;④同旁内角互补,两直线平行.
3.如图,直线AB,CD相交于点O,EO⊥AB于点O,∠EOD=56°23′,则∠BOC的度数为
.
4.如图,∠BOE的对顶角是
.
5.如图,直线AB,CD相交于点O,∠AOC=40°,过点O作射线OE,如果OE⊥OA,那么∠DOE的大小是
度.
6.如图,AB∥CD,且AC⊥BD,垂足为E,∠BAC=α°,则∠BDC=
°(用含α的式子表示).
7.如图,把长方形纸片ABCD沿折痕EF折叠,使点B与点D重合,点A落在点G处,若∠BEF=65°,则∠DFG的度数为
.
8.如图,直线AB∥CD,∠B=60°,∠C=40°,则∠E等于
.
9.(多选)如图,下列条件中能判断直线l1∥l2的有
.
A.∠1=∠2
B.∠4=∠5
C.∠2+∠4=180°
D.∠1=∠3
E.∠6=∠1+∠2
10.如图,AD∥BC,∠ADC=120°,∠BAD=3∠CAD,E为AC上一点,且∠ABE=2∠CBE,在直线AC上取一点P,使∠ABP=∠DCA,则∠CBP:∠ABP的值为
.
11.如图,把一张长方形纸片沿EF折叠后,点D、C分别落在D',C'的位置,若∠AED'=48°,则∠EFB=
.
12.如图,直线m∥n,AB⊥BC,∠1=35°,∠2=62°,则∠BCD的度数为
.
13.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠1=55°,则∠2的度数为
.
14.已知:如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=
.
15.如图,直线AF和AC被直线EB所截,∠EBC的同位角是∠EOF,直线DC、AC被直线AF所截,∠FAC同位角是
.
16.如图,直线AB、CD相交于点O,∠AOC=70°,∠2=30°,则∠1的度数为
.
17.如图,直线AB与直线CD相交于点O,OE平分∠AOC,若∠AOD﹣∠BOD=60°,则∠EOB的度数是
.
18.如图,已知AB∥CD,∠AOC=108°,∠OAH=2∠BAH,∠OCH=2∠HCD,则∠H的度数是
.
19.如图,直线a∥b,将三角尺的直角顶点放在直线b上,若∠1=33°,则∠2=
.
20.把含有30°的直角三角板(∠ABC=30°)如图放置,若EF∥MM,∠1=100°,则∠2的度数为
.
参考答案
1.解:如图所示,过F作FG∥AB,过E作EH∥CD,
∵AB∥CD,
∴EH∥CD∥AB∥CD,
∴∠B+∠BFG=180°,∠GFE=∠FEH,∠CDE=∠DEH,
∵∠DEF=65°,
∴∠GFE+∠CDE=∠FEH+∠DEH=∠FED=65°,
∴∠B+∠BFE+∠FED+∠D=180°+65°×2=310°,
故答案为:310.
2.解:如图,由题图(2)的操作可知PE⊥CD,所以∠PEC=∠PED=90°.由题图(3)的操作可知AB⊥PE,所以∠APE=∠BPE=90°,所以∠PEC=∠PED=∠APE=∠BPE=90°,所以可依据结论②,③或④判定AB∥CD,
故答案为②③④.
3.解:∵EO⊥AB于点O,∠EOD=56°23′,
∴∠BOD=90°﹣56°23′=33°37′,
∴∠BOC的度数为:180°﹣33°37′=146°23′.
故答案为:146°23′.
4.解:如图,∠BOE的对顶角是∠AOF.
故答案是:∠AOF.
5.解:如图所示,
当OE在直线CD上方时,
∵直线AB与直线CD相交,∠AOC=40°,
∴∠BOD=∠AOC=40°.
∵EO⊥AB,
∴∠BOE=90°,
∴∠DOE=∠BOE﹣∠BOD=90°﹣40°=50°;
当OE在OB与OC之间时,
∵∠BOE=90°,
∴∠DOE=∠BOE+∠BOD=90°+40°=130°.
故答案为:50或130
6.解:∵AC⊥BD,∠BAC=α°,
∴∠ABE=90°﹣α°,
又∵AB∥CD,
∴∠BDC=∠ABE=90°﹣α°,
故答案为:(90﹣α).
7.解:∵四边形ABCD是矩形,
∴AD∥BC,
∵∠BEF=65°,
∴∠DFE=∠BEF=65°,∠AFE=180°﹣∠BEF=115°,
由折叠的性质知∠GFE=∠AFE=115°,
则∠DFG=∠GFE﹣∠DFE=50°,
故答案为:50°.
8.解:如图所示:
∵AB∥CD,
∴∠B=∠EFC,
又∵∠B=60°,
∴∠EFC=60°,
又∵∠C+∠E+∠EFC=180°,
∠C=40°,
∴∠E=180°﹣∠C﹣∠EFC
=180°﹣40°﹣60°
=80°
故答案为80°.
9.解:A、∠1和∠2不是直线l1、l2被第三条直线所截形成的角,故不能判断直线l1∥l2.
B、∵∠4=∠5,∴l1∥l2(同位角相等两直线平行).
C、∠2、∠4是直线l1、l2被第三条直线所截形成的同旁内角,故∠2+∠4=180°能判断直线l1∥l2.
D、∵∠1=∠3,∴l1∥l2(内错角相等两直线平行).
E、作l1∥l,∴∠1=∠7,∵∠6=∠7+∠8,∴∠8=∠2,∴l∥l2,∴l1∥l2.
故答案为:BCDE.
10.解:如图,①当∠ABP1=∠DCA时,即∠1=∠2,
∵∠D=120°,
∴∠1+∠3=180°﹣120°=60°,
∵∠BAD=3∠CAD,∠ABE=2∠CBE,AD∥BC,
∴3∠3+3∠EBC=180°,
∴∠3+∠EBC=60°,
∴∠EBC=∠1=∠2=∠P1BE,
∴∠CBP1:∠ABP1的值为2,
②当∠ABP2=∠DCA时,∴∠CBP2:∠ABP2的值为4,
故答案为:2或4.
11.解:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DEF=∠EFB,
又由折叠的性质可得∠D′EF=∠DEF,
∵∠AED′+∠D′EF+∠DEF=180°,∠AED′=50°,
∠D′EF=∠DEF==66°,
∴∠EFB=∠DEF=66°.
故答案为:66°.
12.解:如图,过B作BE∥m,过C作CF∥n,
∵m∥n,
∴m∥BE∥CF∥n,
∴∠ABE=∠1=35°,∠DCF=∠2=62°,
又∵AB⊥BC,
∴∠ABC=90°,
∴∠EBC=90°﹣35°=55°,
∴∠BCF=∠EBC=55°,
∴∠BCD=∠BCF+∠DCF=55°+62°=117°.
故答案为:117°.
13.解:∵EO⊥AB,
∴∠EOB=90°,
∵∠1=55°,
∴∠2=180°﹣90°﹣55°=35°.
故答案为:35°.
14.解:∵∠1+∠2=180°,∠1+∠BDC=180°
∴∠2=∠BDC
∴EF∥AB
∴∠3=∠BDE
∵∠3=∠A
∴∠A=∠BDE
∴AC∥DE
∴∠ACB+∠CED=180°
∵CD平分∠ACB,∠4=35°
∴∠ACB=2∠4=2×35°=70°
∴∠CED=180°﹣∠ACB=180°﹣70°=110°
故答案为:110°.
15.解:根据同位角的图形特点,可得∠FAC的同位角是∠COF,
故答案为∠COF.
16.解:∵∠AOC=∠BOD=70°,∠2=30°,
∴∠1=∠BOD﹣∠2=70°﹣30°=40°,
故答案为:40°.
17.解:∵∠AOD+∠DOB=180°,∠AOD﹣∠DOB=60°,
∴∠AOD=120°,∠DOB=60°,
∴∠AOC=∠DOB=60°,∠BOC=∠AOD=120°,
∵OE平分∠AOC,
∴∠EOC=∠AOC=30°,
∴∠EOB=∠EOC+∠BOC=150°.
故答案为:150°.
18.解:过点O作OE∥AB,过点H作HF∥AB,则AB∥OE∥HF∥CD,
∴∠BAO+∠AOE=∠OCD+∠EOC=180°,
∵∠AOC=∠AOE+EOC=108°,
∴∠BAO+∠OCD=180°+180°﹣108°=252°,
∵∠OAH=2∠BAH,∠OCH=2∠DCH,
∴∠BAH+∠DCH=(∠BAO+∠OCD)=84°,
∵AB∥HF∥CD,
∴∠BAH=∠AHF,∠DCH=∠CHF,
∴∠AHC=∠AHF+∠CHF=∠BAH+∠DCH=84°,
故答案为:84°.
19.解:∵∠1+90°+∠3=180°,∠1=33°,
∴∠3=57°.
∵直线a∥b,
∴∠2=∠3=57°.
故答案为:57°.
20.解:∵EF∥MM,
∴∠3=∠1=100°.
∵∠3+∠4=180°,
∴∠4=180°﹣100°=80°.
∵∠4=∠5+∠ABC,∠ABC=30°,
∴∠5=80°﹣30°=50°,
∴∠2=180°﹣50°=130°.
故答案为:130°.
第1页(共1页)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
