2020-2021学年 苏科版七年级数学下册7.5 多边形的内角和与外角和 同步练习(一)(word版含答案)
文档属性
| 名称 | 2020-2021学年 苏科版七年级数学下册7.5 多边形的内角和与外角和 同步练习(一)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 218.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 00:00:00 | ||
图片预览



文档简介
2020-2021学年七年级数学苏科版下册
7.5
多边形的内角和与外角和
同步练习(一)
1.科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射出去,若b镜反射出的光线n平行于m,且∠1=30°,则∠2=
,∠3=
;
(2)在(1)中,若∠1=70°,则∠3=
;若∠1=a,则∠3=
;
(3)由(1)(2)请你猜想:当∠3=
时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.(提示:三角形的内角和等于180°)
2.已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明:∠ABC=∠BFD;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.
3.如图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系:
;
(2)如图2,∠1+∠2+∠3+∠4+∠5+∠6+∠7=
度
(3)如图3所示,已知∠1=∠2,∠3=∠4,猜想∠B,∠P,∠D之间的数量关系,并证明.
4.【概念学习】
在平面中,我们把大于180°且小于360°的角称为优角.如果两个角相加等于360°,那么称这两个角互为组角,简称互组.
(1)若∠1、∠2互为组角,且∠1=135°,则∠2=
°
【理解应用】
习惯上,我们把有一个内角大于180°的四边形俗称为镖形.
(2)如图①,在镖形ABCD中,优角∠BCD与钝角∠BCD
互为组角,试探索内角∠A、∠B、∠D与钝角∠BCD之间的数量关系,并说明理由.
【拓展延伸】
(3)如图②,已知四边形ABCD中,延长AD、BC交于点Q,延长AB、DC交于P,∠APD、∠AQB的平分线交于点M,∠A+∠QCP=180°.
①写出图中一对互组的角
(两个平角除外);
②直接运用(2)中的结论,试说明:PM⊥QM.
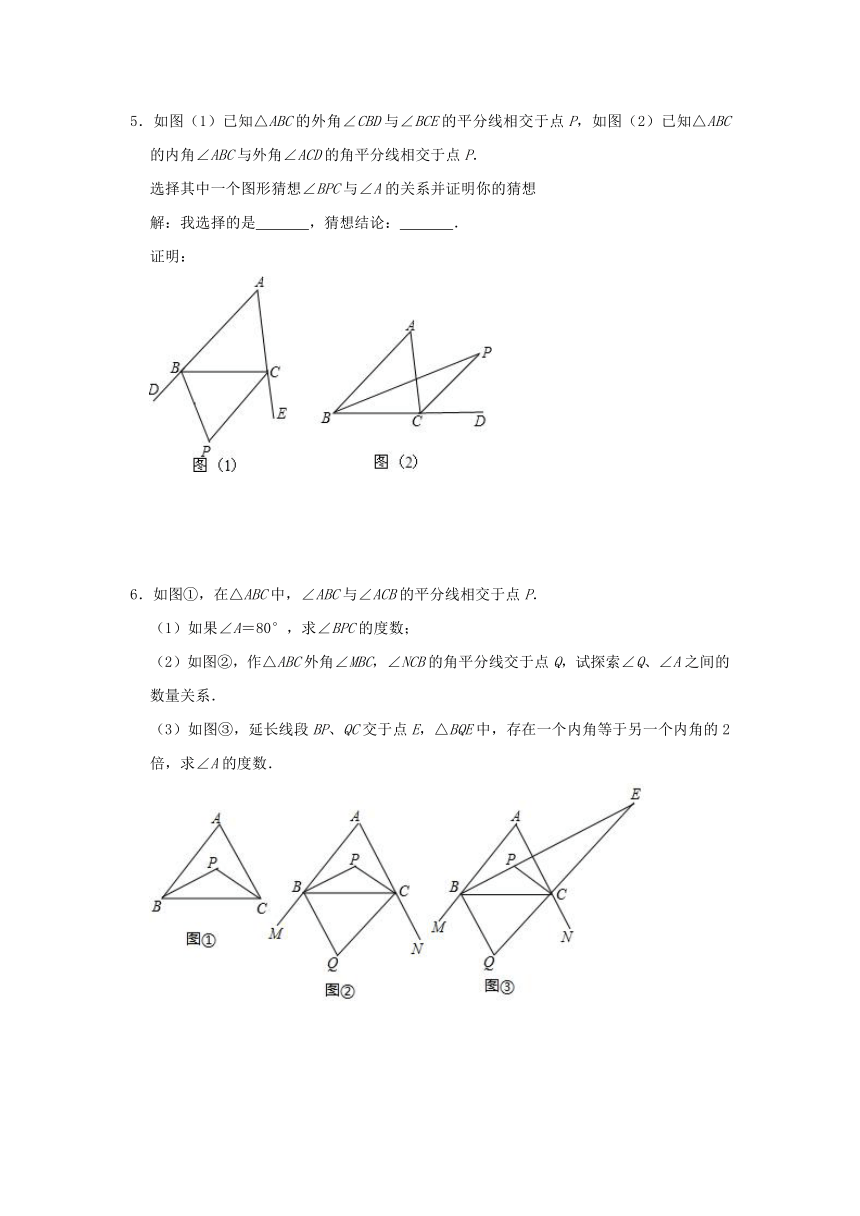
5.如图(1)已知△ABC的外角∠CBD与∠BCE的平分线相交于点P,如图(2)已知△ABC的内角∠ABC与外角∠ACD的角平分线相交于点P.
选择其中一个图形猜想∠BPC与∠A的关系并证明你的猜想
解:我选择的是
,猜想结论:
.
证明:
6.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
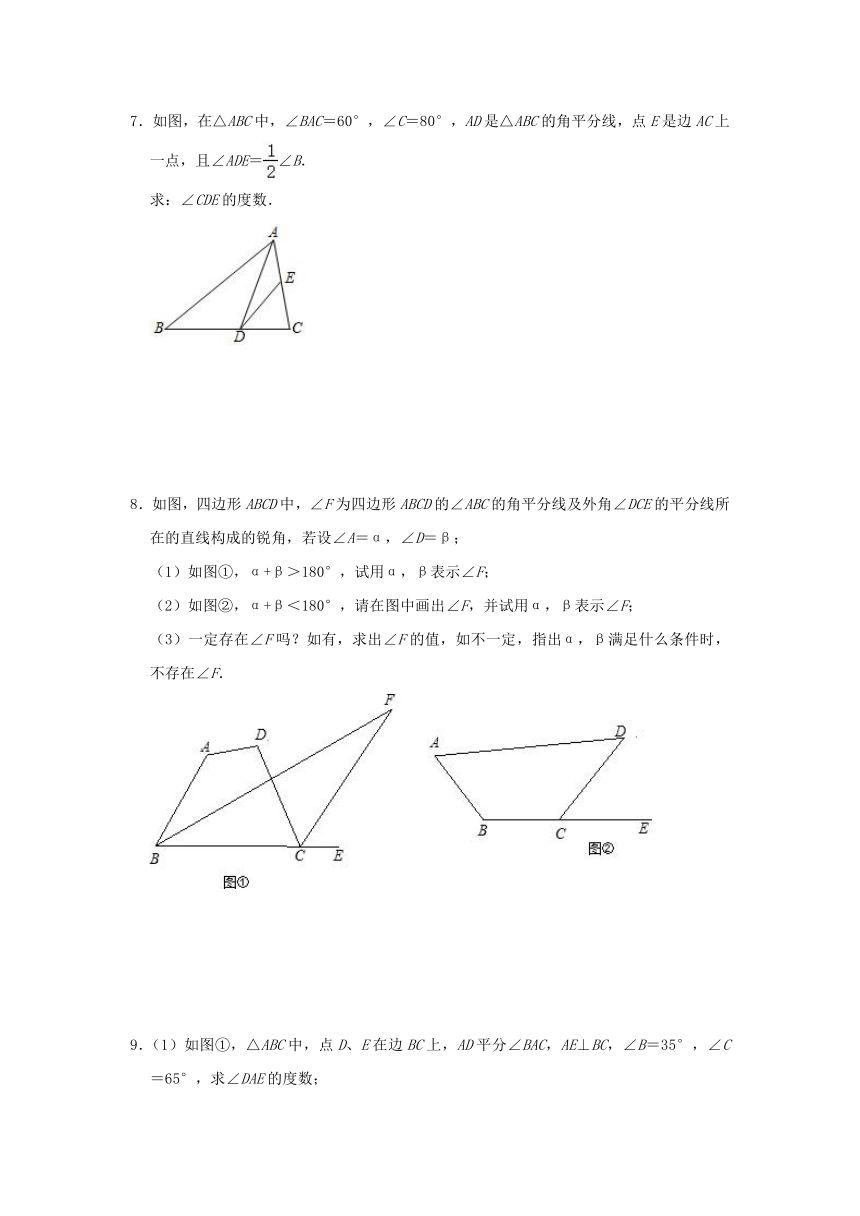
7.如图,在△ABC中,∠BAC=60°,∠C=80°,AD是△ABC的角平分线,点E是边AC上一点,且∠ADE=∠B.
求:∠CDE的度数.
8.如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β;
(1)如图①,α+β>180°,试用α,β表示∠F;
(2)如图②,α+β<180°,请在图中画出∠F,并试用α,β表示∠F;
(3)一定存在∠F吗?如有,求出∠F的值,如不一定,指出α,β满足什么条件时,不存在∠F.
9.(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?
10.已知:在△ABC和△DEF中,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,若∠A=50°,∠E+∠F=100°,则∠ABD+∠ACD=
度.
(2)当将△DEF如图2摆放时,∠A=m°,∠E+∠F=n°,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论
(填“能”或“不能”)
11.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为
°,△AOB
.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC
(填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
12.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
13.如图,AD,AE分别是△ABC的高和角平分线.
(1)已知∠B=40°,∠C=60°,求∠DAE的度数;
(2)设∠B=α,∠C=β(α<β).请直接写出用α、β表示∠DAE的关系式
.
14.已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC=
°,∠BQC=
°;
(2)当α=
°时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系:
.
15.阅读:如图1,CE∥AB,所以∠1=∠A,∠2=∠B.所以∠ACD=∠1+∠2=∠A+∠B.这是一个有用的结论,请用这个结论,在图2的四边形ABCD内引一条和一边平行的直线,求∠A+∠B+∠C+∠D的度数.
参考答案
1.解:(1)∵∠1=30°,
∴∠4=∠1=30°,
∴∠6=180°﹣30°﹣30°=120°,
∵m∥n,
∴∠7+∠6=180°,
∴∠2=60°,
∴∠7=60°,
∴∠3=180°﹣60°﹣30°=90°,
故答案为:60°,90°;
(2)∵∠1=70°,
∴∠4=∠1=70°,
∴∠6=180°﹣70°﹣70°=40°,
∵m∥n,
∴∠7+∠6=180°,
∴∠7=140°,
∴∠2=20°,
∴∠3=180°﹣20°﹣70°=90°;
∵∠1=a°,
∴∠4=∠1=a°,
∴∠6=180°﹣a°﹣a°=180°﹣2a,
∵m∥n,
∴∠7+∠6=180°,
∴∠7=2a°,
∴∠5=∠2=90°﹣a,
∴∠3=180°﹣90°+a﹣a=90°;
故答案为:90°;90°;
(3)猜想:当∠3=90°时,m总平行于n,
理由:∵△的内角和为180°,又∠3=90°,
∴∠4+∠5=90°
∵∠4=∠1∠5=∠2,
∴∠1+∠2=90°,
∴∠1+∠4+∠5+∠2=90°+90°=180°,
∵∠1+∠4+∠6+∠5+∠2+∠7=180°+180°=360°,
∴∠6+∠7=180°
∴m∥n(同旁内角互补,而直线平行)
故答案为:90°
2.解:(1)∵∠BFD=∠ABF+∠BAD,∠ABC=∠ABF+∠FBC,
∵∠BAD=∠EBC,
∴∠ABC=∠BFD;
(2)∵∠BFD=∠ABC=35°,
∵EG∥AD,
∴∠BEG=∠BFD=35°,
∵EH⊥BE,
∴∠BEH=90°,
∴∠HEG=∠BEH﹣∠BEG=55°.
3.解:(1)如图1,∵∠A+∠B+∠AOB=∠C+∠D+∠COD=180°,∠AOB=∠DOC,
∴∠A+∠B=∠C+∠D;
故答案为:∠A+∠B=∠C+∠D;
(2)∵∠6,∠7的和与∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°.
(3)∠1+∠D=∠P+∠3①,∠4+∠B=∠2+∠P②,
如图3,∵∠1=∠2,∠3=∠4,
①+②得:
∠1+∠D+∠4+∠B=∠P+∠3+∠2+∠P,
即2∠P=∠D+∠B.
4.解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°﹣∠1=225°;
(2)钝角∠BCD=∠A+∠B+∠D.理由如下:
如图①,∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360°?,
∴钝角∠BCD=∠A+∠B+∠D;
(3)①优角∠PCQ与钝角∠PCQ;
②∵∠APD、∠AQB的平分线交于点M,
∴∠AQM=∠BQM,∠APM=∠DPM.
令∠AQM=∠BQM=α,∠APM=∠DPM=β.
∵在镖形APMQ中,有∠A+α+β=∠PMQ,
在镖形APCQ中,有∠A+2α+2β=∠QCP,
∴∠QCP+∠A=2∠PMQ,
∵∠A+∠QCP=180°,
∴∠PMQ=90°.
∴PM⊥QM.
故答案为225;优角∠PCQ与钝角∠PCQ.
5.解:图(1)
∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A,
∵BP,CP分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180+∠A)°,
即:∠BPC=180°﹣(∠PBC+∠PCB)=(90﹣∠A)°;
图(2),结论:∠BPC=∠A.
证明如下:
∵∠1是△PBC的外角,
∴∠P=∠1﹣∠2=(∠ACD﹣∠ABC)=∠A.
6.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
7.解:∵在△ABC中,∠BAC=60°,∠C=80°,
∴∠B=180°﹣60°﹣80°=40°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠B+∠BAD=70°,
∵∠ADE=∠B=20°,
∴∠CDE=∠ADC﹣∠ADE=70°﹣20°=50°.
8.解:(1)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠FBC+(180°﹣2∠DCF)=180°﹣2(∠DCF﹣∠FBC)=180°﹣2∠F,
∴360°﹣(α+β)=180°﹣2∠F,
2∠F=α+β﹣180°,
∴∠F=(α+β)﹣90°;
(2)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠GBC+(180°﹣2∠HCE)=180°+2(∠GBC﹣∠HCE)=180°+2∠F,
∴360°﹣(α+β)=180°+2∠F,
∠F=90°﹣(α+β);
(3)α+β=180°时,不存在∠F.
9.解:(1)∠BAC=180°﹣∠B﹣∠C=180°﹣35°﹣65°=80°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=40°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°﹣∠B=55°,
∴∠DAE=∠BAE﹣∠BAD=55°﹣40°=15°;
(2)作AH⊥BC于H,如图②,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(3)作AH⊥BC于H,如图③,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
10.解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=50°
∴∠ABC+∠ACB=180°﹣50°=130°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=130°+100°=230°.
(2)∠ABD+∠ACD=(180﹣m﹣n)°;
理由如下:
∵∠E+∠F=n°
∴∠CBD+∠BCD=∠E+∠F=n°
∴∠ABD+∠ACD=∠ABC+∠ACB﹣(∠BCD+∠CBD)=(180﹣m﹣n)°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.假设∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
11.解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
12.解:设这个多边形的边数为n,根据题意,得
(n﹣2)?180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
13.解:(1)∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵AE是角平分线,
∴∠BAE=∠BAC=×80°=40°,
∵AD是高,
∴∠BAD=90°﹣∠B=90°﹣40°=50°,
∴∠DAE=∠BAD﹣∠BAE=50°﹣40°=10°;
(2)∵∠B=α,∠C=β(α<β),
∴∠BAC=180°﹣(α+β),
∵AE是角平分线,
∴∠BAE=∠BAC=90°﹣(α+β),
∵AD是高,
∴∠BAD=90°﹣∠B=90°﹣α,
∴∠DAE=∠BAD﹣∠BAE=90°﹣α﹣[90°﹣(α+β)]=(β﹣α);
故答案为:(β﹣α).
14.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α,
∴(∠DBC+∠BCE)=180°,
即(180°+α)=180°,
解得α=60°;
(3)∵α=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°;
(4)∵α>60°,
∠BPC=90°﹣α、
∠BQC=135°﹣α、
∠BOC=α﹣45°.
∠BPC、∠BQC、∠BOC三角之间的数量关系:∠BPC+∠BQC+∠BOC=(90°﹣α)+(135°﹣α)+(α﹣45°)=180°.
故答案为:70,125;60;∠BPC+∠BQC+∠BOC=180°.
15.解:作DE∥AB,交BC于E,由题意,∠DEB=∠C+∠EDC,
∴∠A+∠ADE=180°,∠B+∠DEB=180°,
则∠A+∠B+∠C+∠ADC
=∠A+∠B+∠C+∠EDC+∠ADE
=∠A+∠B+∠DEB+∠ADE
=360°.
7.5
多边形的内角和与外角和
同步练习(一)
1.科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b镜反射出去,若b镜反射出的光线n平行于m,且∠1=30°,则∠2=
,∠3=
;
(2)在(1)中,若∠1=70°,则∠3=
;若∠1=a,则∠3=
;
(3)由(1)(2)请你猜想:当∠3=
时,任何射到平面镜a上的光线m经过平面镜a和b的两次反射后,入射光线m与反射光线n总是平行的?请说明理由.(提示:三角形的内角和等于180°)
2.已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明:∠ABC=∠BFD;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.
3.如图1我们称之为“8字形”,请直接写出∠A,∠B,∠C,∠D之间的数量关系:
;
(2)如图2,∠1+∠2+∠3+∠4+∠5+∠6+∠7=
度
(3)如图3所示,已知∠1=∠2,∠3=∠4,猜想∠B,∠P,∠D之间的数量关系,并证明.
4.【概念学习】
在平面中,我们把大于180°且小于360°的角称为优角.如果两个角相加等于360°,那么称这两个角互为组角,简称互组.
(1)若∠1、∠2互为组角,且∠1=135°,则∠2=
°
【理解应用】
习惯上,我们把有一个内角大于180°的四边形俗称为镖形.
(2)如图①,在镖形ABCD中,优角∠BCD与钝角∠BCD
互为组角,试探索内角∠A、∠B、∠D与钝角∠BCD之间的数量关系,并说明理由.
【拓展延伸】
(3)如图②,已知四边形ABCD中,延长AD、BC交于点Q,延长AB、DC交于P,∠APD、∠AQB的平分线交于点M,∠A+∠QCP=180°.
①写出图中一对互组的角
(两个平角除外);
②直接运用(2)中的结论,试说明:PM⊥QM.
5.如图(1)已知△ABC的外角∠CBD与∠BCE的平分线相交于点P,如图(2)已知△ABC的内角∠ABC与外角∠ACD的角平分线相交于点P.
选择其中一个图形猜想∠BPC与∠A的关系并证明你的猜想
解:我选择的是
,猜想结论:
.
证明:
6.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
7.如图,在△ABC中,∠BAC=60°,∠C=80°,AD是△ABC的角平分线,点E是边AC上一点,且∠ADE=∠B.
求:∠CDE的度数.
8.如图,四边形ABCD中,∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角,若设∠A=α,∠D=β;
(1)如图①,α+β>180°,试用α,β表示∠F;
(2)如图②,α+β<180°,请在图中画出∠F,并试用α,β表示∠F;
(3)一定存在∠F吗?如有,求出∠F的值,如不一定,指出α,β满足什么条件时,不存在∠F.
9.(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?
10.已知:在△ABC和△DEF中,将△DEF如图摆放,使得∠D的两条边分别经过点B和点C.
(1)当将△DEF如图1摆放时,若∠A=50°,∠E+∠F=100°,则∠ABD+∠ACD=
度.
(2)当将△DEF如图2摆放时,∠A=m°,∠E+∠F=n°,请求出∠ABD+∠ACD的度数,并说明理由;
(3)能否将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB?直接写出结论
(填“能”或“不能”)
11.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°、40°、20°的三角形是“灵动三角形”;三个内角分别为80°、75°、25°的三角形也是“灵动三角形”等等.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).
(1)∠ABO的度数为
°,△AOB
.(填“是”或“不是”)“灵动三角形”;
(2)若∠BAC=70°,则△AOC
(填“是”或“不是”)“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
12.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
13.如图,AD,AE分别是△ABC的高和角平分线.
(1)已知∠B=40°,∠C=60°,求∠DAE的度数;
(2)设∠B=α,∠C=β(α<β).请直接写出用α、β表示∠DAE的关系式
.
14.已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC=
°,∠BQC=
°;
(2)当α=
°时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系:
.
15.阅读:如图1,CE∥AB,所以∠1=∠A,∠2=∠B.所以∠ACD=∠1+∠2=∠A+∠B.这是一个有用的结论,请用这个结论,在图2的四边形ABCD内引一条和一边平行的直线,求∠A+∠B+∠C+∠D的度数.
参考答案
1.解:(1)∵∠1=30°,
∴∠4=∠1=30°,
∴∠6=180°﹣30°﹣30°=120°,
∵m∥n,
∴∠7+∠6=180°,
∴∠2=60°,
∴∠7=60°,
∴∠3=180°﹣60°﹣30°=90°,
故答案为:60°,90°;
(2)∵∠1=70°,
∴∠4=∠1=70°,
∴∠6=180°﹣70°﹣70°=40°,
∵m∥n,
∴∠7+∠6=180°,
∴∠7=140°,
∴∠2=20°,
∴∠3=180°﹣20°﹣70°=90°;
∵∠1=a°,
∴∠4=∠1=a°,
∴∠6=180°﹣a°﹣a°=180°﹣2a,
∵m∥n,
∴∠7+∠6=180°,
∴∠7=2a°,
∴∠5=∠2=90°﹣a,
∴∠3=180°﹣90°+a﹣a=90°;
故答案为:90°;90°;
(3)猜想:当∠3=90°时,m总平行于n,
理由:∵△的内角和为180°,又∠3=90°,
∴∠4+∠5=90°
∵∠4=∠1∠5=∠2,
∴∠1+∠2=90°,
∴∠1+∠4+∠5+∠2=90°+90°=180°,
∵∠1+∠4+∠6+∠5+∠2+∠7=180°+180°=360°,
∴∠6+∠7=180°
∴m∥n(同旁内角互补,而直线平行)
故答案为:90°
2.解:(1)∵∠BFD=∠ABF+∠BAD,∠ABC=∠ABF+∠FBC,
∵∠BAD=∠EBC,
∴∠ABC=∠BFD;
(2)∵∠BFD=∠ABC=35°,
∵EG∥AD,
∴∠BEG=∠BFD=35°,
∵EH⊥BE,
∴∠BEH=90°,
∴∠HEG=∠BEH﹣∠BEG=55°.
3.解:(1)如图1,∵∠A+∠B+∠AOB=∠C+∠D+∠COD=180°,∠AOB=∠DOC,
∴∠A+∠B=∠C+∠D;
故答案为:∠A+∠B=∠C+∠D;
(2)∵∠6,∠7的和与∠8,∠9的和相等,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=∠1+∠2+∠3+∠4+∠5+∠8+∠9=540°.
(3)∠1+∠D=∠P+∠3①,∠4+∠B=∠2+∠P②,
如图3,∵∠1=∠2,∠3=∠4,
①+②得:
∠1+∠D+∠4+∠B=∠P+∠3+∠2+∠P,
即2∠P=∠D+∠B.
4.解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°﹣∠1=225°;
(2)钝角∠BCD=∠A+∠B+∠D.理由如下:
如图①,∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360°?,
∴钝角∠BCD=∠A+∠B+∠D;
(3)①优角∠PCQ与钝角∠PCQ;
②∵∠APD、∠AQB的平分线交于点M,
∴∠AQM=∠BQM,∠APM=∠DPM.
令∠AQM=∠BQM=α,∠APM=∠DPM=β.
∵在镖形APMQ中,有∠A+α+β=∠PMQ,
在镖形APCQ中,有∠A+2α+2β=∠QCP,
∴∠QCP+∠A=2∠PMQ,
∵∠A+∠QCP=180°,
∴∠PMQ=90°.
∴PM⊥QM.
故答案为225;优角∠PCQ与钝角∠PCQ.
5.解:图(1)
∵∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,
∴∠DBC+∠ECB
=∠A+∠ACB+∠A+∠ABC
=180°+∠A,
∵BP,CP分别是△ABC外角∠DBC,∠BCE的角平分线,
∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180+∠A)°,
即:∠BPC=180°﹣(∠PBC+∠PCB)=(90﹣∠A)°;
图(2),结论:∠BPC=∠A.
证明如下:
∵∠1是△PBC的外角,
∴∠P=∠1﹣∠2=(∠ACD﹣∠ABC)=∠A.
6.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
7.解:∵在△ABC中,∠BAC=60°,∠C=80°,
∴∠B=180°﹣60°﹣80°=40°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠B+∠BAD=70°,
∵∠ADE=∠B=20°,
∴∠CDE=∠ADC﹣∠ADE=70°﹣20°=50°.
8.解:(1)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠FBC+(180°﹣2∠DCF)=180°﹣2(∠DCF﹣∠FBC)=180°﹣2∠F,
∴360°﹣(α+β)=180°﹣2∠F,
2∠F=α+β﹣180°,
∴∠F=(α+β)﹣90°;
(2)∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠GBC+(180°﹣2∠HCE)=180°+2(∠GBC﹣∠HCE)=180°+2∠F,
∴360°﹣(α+β)=180°+2∠F,
∠F=90°﹣(α+β);
(3)α+β=180°时,不存在∠F.
9.解:(1)∠BAC=180°﹣∠B﹣∠C=180°﹣35°﹣65°=80°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=40°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°﹣∠B=55°,
∴∠DAE=∠BAE﹣∠BAD=55°﹣40°=15°;
(2)作AH⊥BC于H,如图②,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(3)作AH⊥BC于H,如图③,
由(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠DAH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
10.解:(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=50°
∴∠ABC+∠ACB=180°﹣50°=130°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=130°+100°=230°.
(2)∠ABD+∠ACD=(180﹣m﹣n)°;
理由如下:
∵∠E+∠F=n°
∴∠CBD+∠BCD=∠E+∠F=n°
∴∠ABD+∠ACD=∠ABC+∠ACB﹣(∠BCD+∠CBD)=(180﹣m﹣n)°;
(3)不能.假设能将△DEF摆放到某个位置时,使得BD、CD同时平分∠ABC和∠ACB.假设∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,与三角形内角和定理矛盾,所以不能.
11.解:(1)∵AB⊥OM,
∴∠BAO=90°,
∵∠AOB=60°,
∴∠ABO=90°﹣60°=30°,
∵90°=3×30°,
∴△AOB是“灵动三角形”.
故答案为:30,是.
(2)∵∠OAB=90°,∠BAC=70°,
∴∠OAC=20°,
∵∠AOC=60°=3×20°,
∴△AOC是“灵动三角形”.
故答案为:是.
(3:①∠ACB=3∠ABC时,∠CAB=60°,∠OAC=30°;
②当∠ABC=3∠CAB时,∠CAB=10°,∠OAC=80°.
③当∠ACB=3∠CAB时,∠CAB=37.5°,可得∠OAC=52.5°.
综上所述,满足条件的值为30°或52.5°或80°.
12.解:设这个多边形的边数为n,根据题意,得
(n﹣2)?180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
13.解:(1)∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵AE是角平分线,
∴∠BAE=∠BAC=×80°=40°,
∵AD是高,
∴∠BAD=90°﹣∠B=90°﹣40°=50°,
∴∠DAE=∠BAD﹣∠BAE=50°﹣40°=10°;
(2)∵∠B=α,∠C=β(α<β),
∴∠BAC=180°﹣(α+β),
∵AE是角平分线,
∴∠BAE=∠BAC=90°﹣(α+β),
∵AD是高,
∴∠BAD=90°﹣∠B=90°﹣α,
∴∠DAE=∠BAD﹣∠BAE=90°﹣α﹣[90°﹣(α+β)]=(β﹣α);
故答案为:(β﹣α).
14.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α,
∴(∠DBC+∠BCE)=180°,
即(180°+α)=180°,
解得α=60°;
(3)∵α=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°;
(4)∵α>60°,
∠BPC=90°﹣α、
∠BQC=135°﹣α、
∠BOC=α﹣45°.
∠BPC、∠BQC、∠BOC三角之间的数量关系:∠BPC+∠BQC+∠BOC=(90°﹣α)+(135°﹣α)+(α﹣45°)=180°.
故答案为:70,125;60;∠BPC+∠BQC+∠BOC=180°.
15.解:作DE∥AB,交BC于E,由题意,∠DEB=∠C+∠EDC,
∴∠A+∠ADE=180°,∠B+∠DEB=180°,
则∠A+∠B+∠C+∠ADC
=∠A+∠B+∠C+∠EDC+∠ADE
=∠A+∠B+∠DEB+∠ADE
=360°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
