2020-2021学年鲁教版(五四制)八年级数学下册第9章图形的相似 单元测试A-(word版含答案)
文档属性
| 名称 | 2020-2021学年鲁教版(五四制)八年级数学下册第9章图形的相似 单元测试A-(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 201.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 22:47:23 | ||
图片预览



文档简介
第九章《图形的相似》单元测试题(A)
一、选择题(将答案填在下面答题栏中)
1.下列说法正确的是(
)
A.所有边都分别成比例的多边形相似 B.所有角都分别相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
2.若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2
B.3∶5
C.9∶4
D.4∶9
3.如图,下列条件不能判定△ADB
∽△ABC的是( )
(
)A.∠ABD=∠ACB
B.∠ADB=∠ABC
C.AB2=AD·AC
D.=
4.如图,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是
( )
5.如果线段a、b、c、d满足ad=bc,则下列各式中不成立的是(
)
A、
B、
C、
D、
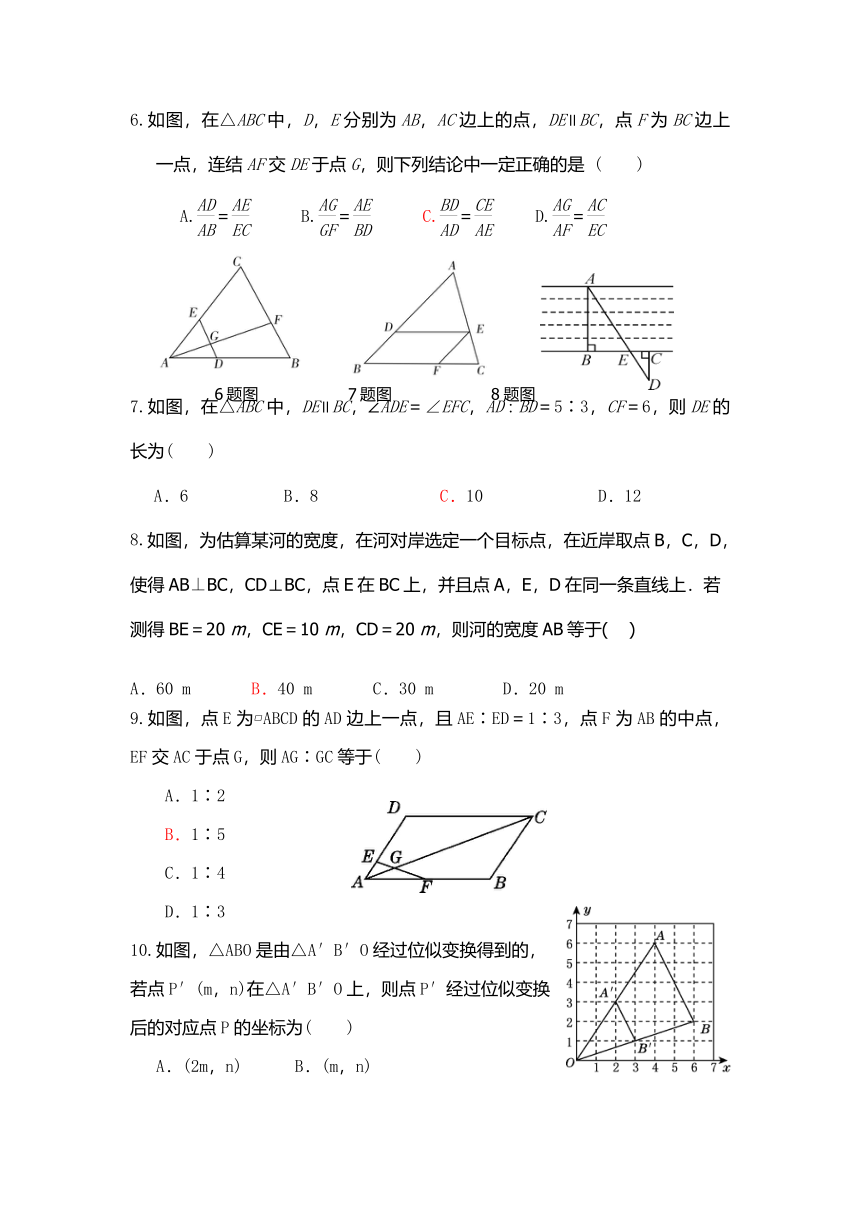
6.如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点F为BC边上一点,连结AF交DE于点G,则下列结论中一定正确的是
( )
(
6题图
7题图
8题图
)A.=
B.=
C.=
D.=
7.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为( )
A.6
B.8
C.10
D.12
8.如图,为估算某河的宽度,在河对岸选定一个目标点,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于(
)
A.60
m
B.40
m
C.30
m
D.20
m
9.如图,点E为?ABCD的AD边上一点,且AE∶ED=1∶3,点F为AB的中点,EF交AC于点G,则AG∶GC等于( )
A.1∶2
B.1∶5
C.1∶4
D.1∶3
10.如图,△ABO是由△A′B′O经过位似变换得到的,
若点P′(m,n)在△A′B′O上,则点P′经过位似变换
后的对应点P的坐标为( )
A.(2m,n)
B.(m,n)
C.(m,2n)
D.(2m,2n)
11.宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD,BC的中点E,F,连结EF;以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是(
)
A.矩形ABFE
B.矩形EFCD
C.矩形EFGH
D.矩形DCGH
12.如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连结BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是( )
①②③④
B.①④
C.②③④
D.①②③
二、填空题
13.如图,直线l1,l2,…,l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3,l6相交于点B,E,C,F,若BC=2,则EF的长是
.
(
13题图
14题图
)14.
如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为
.
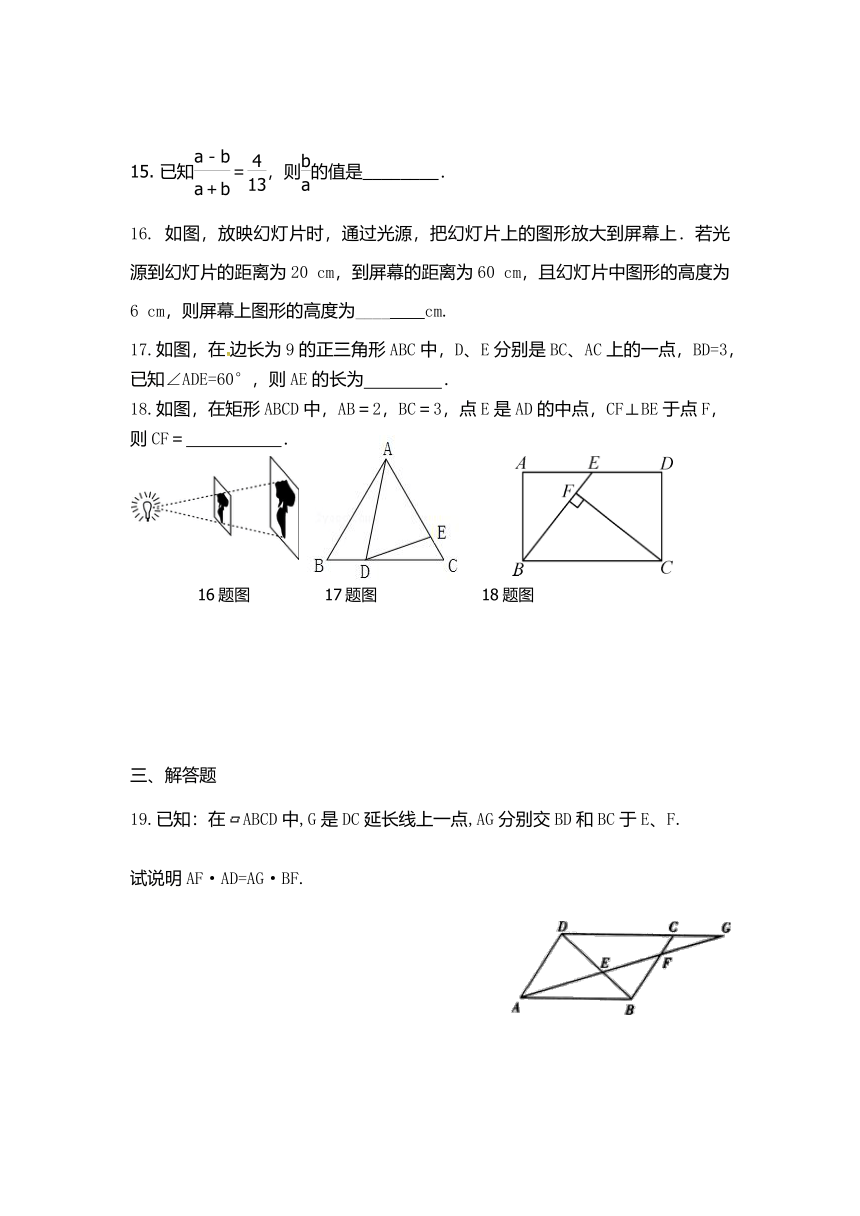
15.
已知=,则的值是________.
16.
如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20
cm,到屏幕的距离为60
cm,且幻灯片中图形的高度为6
cm,则屏幕上图形的高度为____
cm.
17.如图,在边长为9的正三角形ABC中,D、E分别是BC、AC上的一点,BD=3,已知∠ADE=60°,则AE的长为
.
(
16题图
17题图
18题图
)18.如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF=
.
三、解答题
19.已知:在ABCD中,G是DC延长线上一点,AG分别交BD和BC于E、F.
试说明AF·AD=AG·BF.
20.如图,点D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.
21.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加辅助线);
(2)请分别说明两对三角形相似的理由.
22.
如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
23.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
24.如图,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
25.如图,明珠大厦的顶部建有一直径为16
m的“明珠”,它的西面45
m处有一高16
m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12
m.求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度).
第九章《图形的相似》单元测试题(A)参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
C
B
C
C
B
B
D
D
D
二、填空题
13、
5
14、7
15、
16、18
17、7
18、
三、解答题
19、8米.
20、解:在△ABD和△ACB中,∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,∴=,
∵AB=6,AD=4,∴AC===9,
则CD=AC-AD=9-4=5
21、解:(1)△ABC∽△ADE,△ABD∽△ACE;
(2)∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.
又∵∠ABC=∠ADE,
∴△ABC∽△ADE,∴=.
又∵∠BAD=∠CAE,∴△ABD∽△ACE.
22、解:(1)∵AB=AC,∴∠B=∠C.∵∠APD=∠B,∴∠APD=∠B=∠C.∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC,∴△ABP∽△PCD,∴=,∴AB·CD=CP·BP.∵AB=AC,∴AC·CD=CP·BP
(2)∵PD∥AB,∴∠APD=∠BAP.∵∠APD=∠C,∴∠BAP=∠C.∵∠B=∠B,∴△BAP∽△BCA,∴=.∵AB=10,BC=12,∴=,∴BP=
23、(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC
.∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,∴△ADF∽△DEC
∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得AE===6
24、
解:(1)
∵四边形ABCD是正方形,∴∠B=90°,AD∥BC,∴∠AMB=∠EAF,又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EFA
(2)
由勾股定理得AM==13,∵F是AM的中点,∴AF=AM=6.5,∵△ABM∽△EFA,∴=,即=,∴AE=16.9,∴DE=AE-AD=16.9-12=4.9
25、解:设AE=h,∵CD∥AB,∴△FAB∽△FCD,∴=,
即=,∴AF=.
同理易证△AGE∽△CGD,∴=,
即=,∴AG=.
又∵AG-AF=12,∴-=12.
整理得h2-16h-960=0,
∴h=40或h=-24(不合题意,舍去).
∴大厦主体建筑的高度AE为40
m.
一、选择题(将答案填在下面答题栏中)
1.下列说法正确的是(
)
A.所有边都分别成比例的多边形相似 B.所有角都分别相等的多边形相似
C.边数相同的正多边形相似
D.矩形都相似
2.若△ABC∽△DEF,相似比为3∶2,则对应高的比为( )
A.3∶2
B.3∶5
C.9∶4
D.4∶9
3.如图,下列条件不能判定△ADB
∽△ABC的是( )
(
)A.∠ABD=∠ACB
B.∠ADB=∠ABC
C.AB2=AD·AC
D.=
4.如图,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是
( )
5.如果线段a、b、c、d满足ad=bc,则下列各式中不成立的是(
)
A、
B、
C、
D、
6.如图,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点F为BC边上一点,连结AF交DE于点G,则下列结论中一定正确的是
( )
(
6题图
7题图
8题图
)A.=
B.=
C.=
D.=
7.如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为( )
A.6
B.8
C.10
D.12
8.如图,为估算某河的宽度,在河对岸选定一个目标点,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20
m,CE=10
m,CD=20
m,则河的宽度AB等于(
)
A.60
m
B.40
m
C.30
m
D.20
m
9.如图,点E为?ABCD的AD边上一点,且AE∶ED=1∶3,点F为AB的中点,EF交AC于点G,则AG∶GC等于( )
A.1∶2
B.1∶5
C.1∶4
D.1∶3
10.如图,△ABO是由△A′B′O经过位似变换得到的,
若点P′(m,n)在△A′B′O上,则点P′经过位似变换
后的对应点P的坐标为( )
A.(2m,n)
B.(m,n)
C.(m,2n)
D.(2m,2n)
11.宽与长的比是(约0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:作正方形ABCD,分别取AD,BC的中点E,F,连结EF;以点F为圆心,以FD为半径画弧,交BC的延长线于点G;作GH⊥AD,交AD的延长线于点H,则图中下列矩形是黄金矩形的是(
)
A.矩形ABFE
B.矩形EFCD
C.矩形EFGH
D.矩形DCGH
12.如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连结BE并延长交AD于点F,已知S△AEF=4,则下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是( )
①②③④
B.①④
C.②③④
D.①②③
二、填空题
13.如图,直线l1,l2,…,l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3,l6相交于点B,E,C,F,若BC=2,则EF的长是
.
(
13题图
14题图
)14.
如图,在直角三角形ABC中(∠C=90°),放置边长分别3,4,x的三个正方形,则x的值为
.
15.
已知=,则的值是________.
16.
如图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为20
cm,到屏幕的距离为60
cm,且幻灯片中图形的高度为6
cm,则屏幕上图形的高度为____
cm.
17.如图,在边长为9的正三角形ABC中,D、E分别是BC、AC上的一点,BD=3,已知∠ADE=60°,则AE的长为
.
(
16题图
17题图
18题图
)18.如图,在矩形ABCD中,AB=2,BC=3,点E是AD的中点,CF⊥BE于点F,则CF=
.
三、解答题
19.已知:在ABCD中,G是DC延长线上一点,AG分别交BD和BC于E、F.
试说明AF·AD=AG·BF.
20.如图,点D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,求线段CD的长.
21.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加辅助线);
(2)请分别说明两对三角形相似的理由.
22.
如图,在△ABC中,AB=AC,点P,D分别是BC,AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
23.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6,AF=4,求AE的长.
24.如图,在正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
25.如图,明珠大厦的顶部建有一直径为16
m的“明珠”,它的西面45
m处有一高16
m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12
m.求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度).
第九章《图形的相似》单元测试题(A)参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
C
B
C
C
B
B
D
D
D
二、填空题
13、
5
14、7
15、
16、18
17、7
18、
三、解答题
19、8米.
20、解:在△ABD和△ACB中,∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,∴=,
∵AB=6,AD=4,∴AC===9,
则CD=AC-AD=9-4=5
21、解:(1)△ABC∽△ADE,△ABD∽△ACE;
(2)∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.
又∵∠ABC=∠ADE,
∴△ABC∽△ADE,∴=.
又∵∠BAD=∠CAE,∴△ABD∽△ACE.
22、解:(1)∵AB=AC,∴∠B=∠C.∵∠APD=∠B,∴∠APD=∠B=∠C.∵∠APC=∠BAP+∠B,∠APC=∠APD+∠DPC,∴∠BAP=∠DPC,∴△ABP∽△PCD,∴=,∴AB·CD=CP·BP.∵AB=AC,∴AC·CD=CP·BP
(2)∵PD∥AB,∴∠APD=∠BAP.∵∠APD=∠C,∴∠BAP=∠C.∵∠B=∠B,∴△BAP∽△BCA,∴=.∵AB=10,BC=12,∴=,∴BP=
23、(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,∴∠C+∠B=180°,∠ADF=∠DEC
.∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,∴△ADF∽△DEC
∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得AE===6
24、
解:(1)
∵四边形ABCD是正方形,∴∠B=90°,AD∥BC,∴∠AMB=∠EAF,又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EFA
(2)
由勾股定理得AM==13,∵F是AM的中点,∴AF=AM=6.5,∵△ABM∽△EFA,∴=,即=,∴AE=16.9,∴DE=AE-AD=16.9-12=4.9
25、解:设AE=h,∵CD∥AB,∴△FAB∽△FCD,∴=,
即=,∴AF=.
同理易证△AGE∽△CGD,∴=,
即=,∴AG=.
又∵AG-AF=12,∴-=12.
整理得h2-16h-960=0,
∴h=40或h=-24(不合题意,舍去).
∴大厦主体建筑的高度AE为40
m.
