第9章图形的相似 单元测试B-2020-2021学年鲁教版(五四制)八年级数学下册(word版含答案)
文档属性
| 名称 | 第9章图形的相似 单元测试B-2020-2021学年鲁教版(五四制)八年级数学下册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 22:45:24 | ||
图片预览



文档简介
鲁教版八年级数学下册
第九章《图形的相似》测试题(B)
一、选择题
1.
如图,已知,那么添加下列一个条件后,仍无法判定∽的是(
)
A.
B.
C.
D.
2.
如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是(
)
A.
B.
C.△ADE∽△ABC
D.S△ADE:S△ABC=
1:2
3.如图,已知,那么下列结论正确的是(
)
A.
B.
C.
D.
4.△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是(
)
A、27
B、12
C、18
D、20
5.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是(
)
6.如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E.在不添加辅助线的情况下,与△AEF相似的三角形有(
)
A.0个
B.1个
C.2个
D.3个
7.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12
m,塔影长DE=18
m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为(
)
A.24m
B.22m
C.20
m
D.18
m
8.一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.现沿底边依次从下往上
裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是(
)
A.第4张
B.第5张
C.第6张
D.第7张
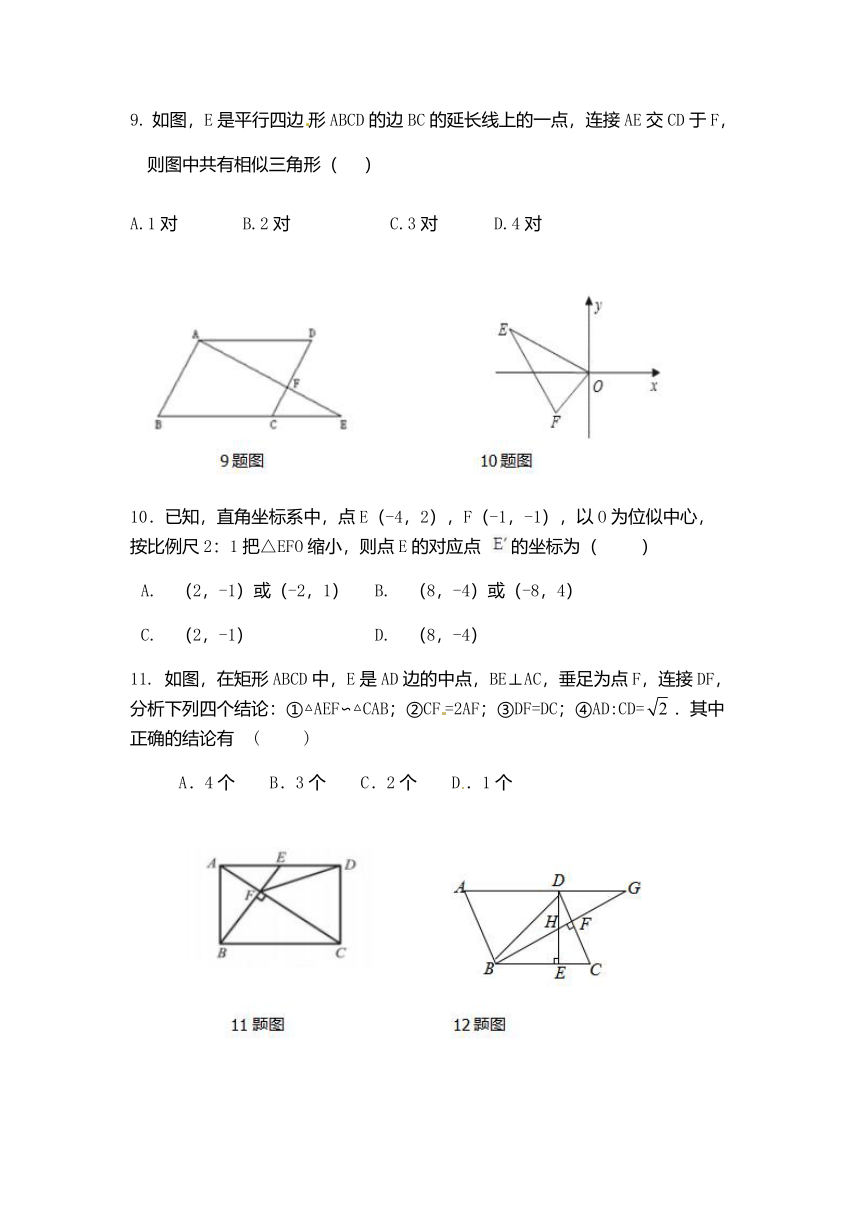
9.
如图,E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于F,则图中共有相似三角形(
)
A.1对
B.2对
C.3对
D.4对
10.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点
的坐标为(
)
A.?(2,-1)或(-2,1)
B.?(8,-4)或(-8,4)???????
C.?(2,-1)????
D.?(8,-4)
11.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④AD:CD=.其中正确的结论有
(
)
A.4个
B.3个
C.2个
D.1个
(
11题图
12题图
)
12.
如图,已知平行四边形ABCD中,,于,于,相交于,的延长线相交于,下面结论:
①②③④
其中正确的结论是(
)
A.①②③④
B.①②③
C.①②④
D.②③④
二、填空题
13.
已知,且,则
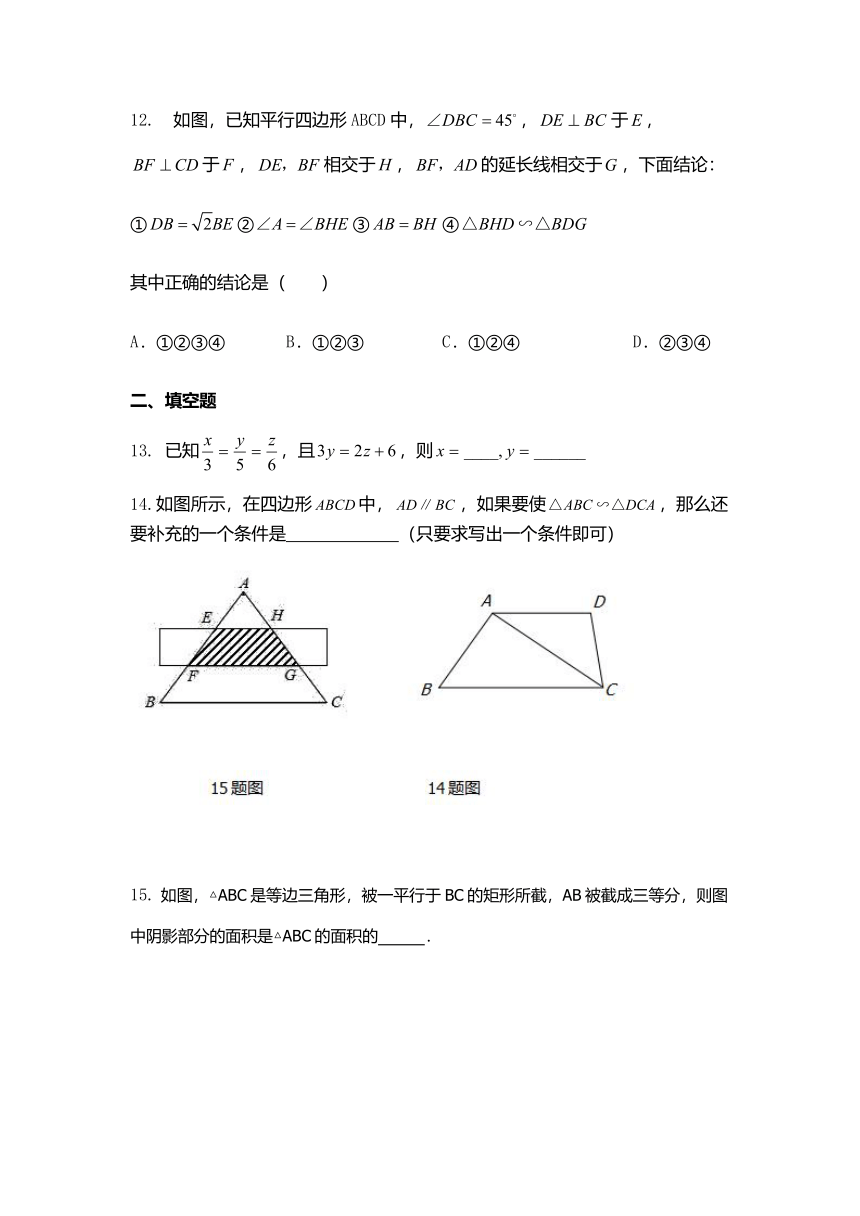
14.如图所示,在四边形中,,如果要使,那么还要补充的一个条件是
(只要求写出一个条件即可)
15.
如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的
.
16.如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是
.
17.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为
.
18.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=________?
三、解答题
19.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,
求BF的长
20.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=
2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=
1.2m,MN=0.8m,求木竿PQ的长度
21.在△ABC中,P为边AB上一点.
(1)如图l,若∠ACP=∠B,求证:AC2
=AP·AB;
(2)若M为CP的中点,AC=2,如图2,若∠PBM=∠ACP,AB=3,求BP的长.
22.如图(1)是一种广场三联漫步机,其侧面示意图如图(2)所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?
23.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
24.
已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD?CE=CD?DE.
25.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC
方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
?
第九章《图形的相似》测试题(B)参考答案
一、选择题
BDACA
CACCA
AB
二、填空题
13.
54
14.
∠D=∠BAC(答案不唯一)
15.1/3
16.144
17.(3,2)
18.1/4
三、解答题
19.2或12/7
20解:如图,过N点作ND⊥PQ于D,
∴
又∵AB=2,BC=1.6,PM=1.2,NM=0.8,
∴
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木竿PQ的长度为2.3米
21解:(1)证明:∵∠ACP=∠B,∠BAC=∠CAP,∴△ACP∽△ABC,∴AC:AB=AP:AC,∴AC2=AP·AB;
(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ
=2x,∵∠PBM=∠ACP,∠PAC=
∠CAQ,∴△APC∽△ACQ,由AC2
=AP·AQ得:22=(3-x)(3+x),∴即
22
解:过A作AF⊥BC,垂足为F,过点D作DH⊥AF,垂足为H.
∵AF⊥BC,垂足为F,∴BF=FC=BC=40cm.
根据勾股定理,得AF===80(cm),
∵∠DHA=∠DAC=∠AFC=90°,
∴∠DAH+∠FAC=90°,∠C+∠FAC=90°,
∴∠DAH=∠C,∴△DAH∽△ACF,
∴=,∴=,∴AH=10cm,
∴HF=(10+80)cm.
答:D到地面的高度为(10+80)cm.
23.(1)证明:∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90°
∵AC=AD,∴∠ACD=∠ADC,∴∠ADC+∠BDC=90°,∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC;
(2)解:过点C作CM⊥PD于点M,∵∠BDC=∠PDC,∴CE=CM,∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴=,设CM=CE=x,∵CE:CP=2:3,∴PC=x,∵AB=AD=AC=1,∴=,解得:x=,故AE=1﹣=.
24.
证明:(1)∵四边形ABCD是平行四边形,
∴BO=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠OED=∠ODE,
∵∠OBE+∠OEB+∠OED+∠ODE=180°,
∴∠BEO+∠DEO=∠BED=90°,
∴DE⊥BE;
(2)∵OE⊥CD
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵OB=OE,
∴∠DBE=∠OEB,
∴∠DBE=∠CDE,
∵∠BED=∠DEC,
∴△BDE∽△DCE,
∴,
∴BD?CE=CD?DE.
25.(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=
=5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t<)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则
或
,
∴=或
=,
∴t=或t=
;
当AD>AE(即t>)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则
或
,
∴=或
=,
解得t=或t=;
综上所述,当t=或
或
或
时,△DEG与△ACB相似.
第九章《图形的相似》测试题(B)
一、选择题
1.
如图,已知,那么添加下列一个条件后,仍无法判定∽的是(
)
A.
B.
C.
D.
2.
如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是(
)
A.
B.
C.△ADE∽△ABC
D.S△ADE:S△ABC=
1:2
3.如图,已知,那么下列结论正确的是(
)
A.
B.
C.
D.
4.△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是(
)
A、27
B、12
C、18
D、20
5.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是(
)
6.如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E.在不添加辅助线的情况下,与△AEF相似的三角形有(
)
A.0个
B.1个
C.2个
D.3个
7.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12
m,塔影长DE=18
m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为(
)
A.24m
B.22m
C.20
m
D.18
m
8.一张等腰三角形纸片,底边长l5cm,底边上的高长22.5cm.现沿底边依次从下往上
裁剪宽度均为3cm的矩形纸条,如图所示.已知剪得的纸条中有一张是正方形,则这张正方形纸条是(
)
A.第4张
B.第5张
C.第6张
D.第7张
9.
如图,E是平行四边形ABCD的边BC的延长线上的一点,连接AE交CD于F,则图中共有相似三角形(
)
A.1对
B.2对
C.3对
D.4对
10.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点
的坐标为(
)
A.?(2,-1)或(-2,1)
B.?(8,-4)或(-8,4)???????
C.?(2,-1)????
D.?(8,-4)
11.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④AD:CD=.其中正确的结论有
(
)
A.4个
B.3个
C.2个
D.1个
(
11题图
12题图
)
12.
如图,已知平行四边形ABCD中,,于,于,相交于,的延长线相交于,下面结论:
①②③④
其中正确的结论是(
)
A.①②③④
B.①②③
C.①②④
D.②③④
二、填空题
13.
已知,且,则
14.如图所示,在四边形中,,如果要使,那么还要补充的一个条件是
(只要求写出一个条件即可)
15.
如图,△ABC是等边三角形,被一平行于BC的矩形所截,AB被截成三等分,则图中阴影部分的面积是△ABC的面积的
.
16.如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是4,9和49.则△ABC的面积是
.
17.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为1:3,点B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为
.
18.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么=________?
三、解答题
19.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,
求BF的长
20.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=
2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=
1.2m,MN=0.8m,求木竿PQ的长度
21.在△ABC中,P为边AB上一点.
(1)如图l,若∠ACP=∠B,求证:AC2
=AP·AB;
(2)若M为CP的中点,AC=2,如图2,若∠PBM=∠ACP,AB=3,求BP的长.
22.如图(1)是一种广场三联漫步机,其侧面示意图如图(2)所示,其中AB=AC=120cm,BC=80cm,AD=30cm,∠DAC=90°.求点D到地面的高度是多少?
23.如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
24.
已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD?CE=CD?DE.
25.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC
方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
?
第九章《图形的相似》测试题(B)参考答案
一、选择题
BDACA
CACCA
AB
二、填空题
13.
54
14.
∠D=∠BAC(答案不唯一)
15.1/3
16.144
17.(3,2)
18.1/4
三、解答题
19.2或12/7
20解:如图,过N点作ND⊥PQ于D,
∴
又∵AB=2,BC=1.6,PM=1.2,NM=0.8,
∴
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木竿PQ的长度为2.3米
21解:(1)证明:∵∠ACP=∠B,∠BAC=∠CAP,∴△ACP∽△ABC,∴AC:AB=AP:AC,∴AC2=AP·AB;
(2)①如图,作CQ∥BM交AB延长线于Q,设BP=x,则PQ
=2x,∵∠PBM=∠ACP,∠PAC=
∠CAQ,∴△APC∽△ACQ,由AC2
=AP·AQ得:22=(3-x)(3+x),∴即
22
解:过A作AF⊥BC,垂足为F,过点D作DH⊥AF,垂足为H.
∵AF⊥BC,垂足为F,∴BF=FC=BC=40cm.
根据勾股定理,得AF===80(cm),
∵∠DHA=∠DAC=∠AFC=90°,
∴∠DAH+∠FAC=90°,∠C+∠FAC=90°,
∴∠DAH=∠C,∴△DAH∽△ACF,
∴=,∴=,∴AH=10cm,
∴HF=(10+80)cm.
答:D到地面的高度为(10+80)cm.
23.(1)证明:∵AB=AD,AC平分∠BAD,∴AC⊥BD,∴∠ACD+∠BDC=90°
∵AC=AD,∴∠ACD=∠ADC,∴∠ADC+∠BDC=90°,∵PD⊥AD,∴∠ADC+∠PDC=90°,∴∠BDC=∠PDC;
(2)解:过点C作CM⊥PD于点M,∵∠BDC=∠PDC,∴CE=CM,∵∠CMP=∠ADP=90°,∠P=∠P,∴△CPM∽△APD,∴=,设CM=CE=x,∵CE:CP=2:3,∴PC=x,∵AB=AD=AC=1,∴=,解得:x=,故AE=1﹣=.
24.
证明:(1)∵四边形ABCD是平行四边形,
∴BO=OD,
∵OE=OB,
∴OE=OD,
∴∠OBE=∠OEB,∠OED=∠ODE,
∵∠OBE+∠OEB+∠OED+∠ODE=180°,
∴∠BEO+∠DEO=∠BED=90°,
∴DE⊥BE;
(2)∵OE⊥CD
∴∠CEO+∠DCE=∠CDE+∠DCE=90°,
∴∠CEO=∠CDE,
∵OB=OE,
∴∠DBE=∠OEB,
∴∠DBE=∠CDE,
∵∠BED=∠DEC,
∴△BDE∽△DCE,
∴,
∴BD?CE=CD?DE.
25.(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=
=5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t<)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则
或
,
∴=或
=,
∴t=或t=
;
当AD>AE(即t>)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则
或
,
∴=或
=,
解得t=或t=;
综上所述,当t=或
或
或
时,△DEG与△ACB相似.
