4.5 垂线(第1课时) 垂线 课件(共23张PPT)
文档属性
| 名称 | 4.5 垂线(第1课时) 垂线 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-10 06:55:49 | ||
图片预览








文档简介
(共21张PPT)
垂
线
第4章
相交线与平行线
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
了解垂线的概念及垂线的有关性质.
【过程与方法】
经历观察、操作、交流、归纳、概括等活动,进一步发展空间概念,提高动手操作技能.
【情感态度】
培养学生合作交流的方法和意识,以及在实际生活中应用数学的意识.
【教学重点】
垂线的概念及垂线的有关性质.
【教学难点】
垂线的应用.
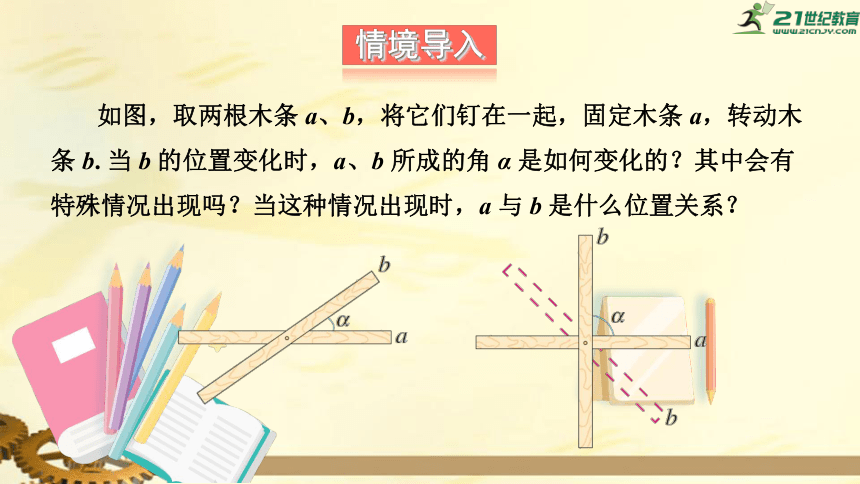
情境导入
如图,取两根木条
a、b,将它们钉在一起,固定木条
a,转动木条
b.
当
b
的位置变化时,a、b
所成的角
α
是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a
与
b
是什么位置关系?
画框的边线,十字路口两条笔直的街道,屋架的横梁与支撑梁等都相交成多少度的角?
观察下图,直线
AB
与直线
CD
有什么位置关系?∠AOD
有多少度?
它们的交点叫做垂足.
两条直线相交所成的四个角中,有一个角是直角时,这两条直线叫做互相垂直.
其中一条直线叫做另一条的垂线.
“垂直”用符号“⊥”表示.
如图,直线
AB
与CD互相垂直,记做“AB⊥CD”.
读做“AB
垂直于
CD”.
观察下图,直线
AB
与直线
CD
有什么位置关系?∠AOD
有多少度?
你能举出一些生活中与垂直有关的实例吗?
两条直线相交不成直角时,其中一条直线叫做另一条直线的斜线,它们的交点叫做斜足.
如图,直线
CD
是
AB
的斜线,同样,直线
AB
也是
CD
的斜线,点
O
是斜足.
(1)如图,在同一平面内,如果
a⊥l,b⊥l,那么
a
//
b
吗?
因为
a⊥l,
b⊥l,
所以∠1
=∠2
=
90
°
,
所以
a∥b
(同位角相等,两直线平行).
(2)如图,在同一平面内,如果直线
a∥b,l⊥a,那么
l
⊥
b
吗?
因为
l⊥a,所以∠1
=
90°.
因为
a∥b,
所以∠2=∠1=90°(两直线平行,同位角相等),
因此
l
⊥
b.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
在如图的简易屋架中,BD,AE,HF
都垂直于
CG,若∠1
=
60°,求∠2
的度数.
解:
因为
BD,AE
都垂直于
CG,
所以∠BDC
=∠AEC
=
90
°
.
所以
BD∥AE
(同位角相等,两直线平行).
从而∠2
=∠1
=
60°(两直线平行,
同位角相等).
如图,已知
CD⊥
AB,∠1=∠2,求∠BFE
的度数.
解:
因为
CD⊥AB,
所以∠BDC
=
90°.
又因为∠1
=∠2,
所以
DC∥EF
(
).
所以∠BEF
=∠BDC
=
90°
(
).
同位角相等,两直线平行
在同一平面内,如果一条直线垂直于
两条平行线中的一条,那么这条直线垂直于另一条
练
习
解:因为
EO⊥CD,所以∠COE=∠DOE=90°.
因为∠BOE
=
60°,所以∠BOD
=
30°,
所以
∠AOC
=
∠BOD
=
30°(对顶角相等)
1.
如图,直线
AB,CD
相交于点
O,
EO⊥CD,
∠BOE
=
60°,求∠AOC
的度数.
2.
如图,
DA⊥AB,CD⊥DA,∠B=56°,求∠C.
解:因为
DA⊥AB,
CD⊥DA,
所以
CD∥
AB
.(在同一平面内,垂直于同一条直线的两条直线平行)
所以∠B
+∠C=180°,
所以∠C
=180°-56°=124°
随堂演练
110°、70°、110°
1.
两条直线相交形成四个角,如果其中一个角为70°,则另外三个角的度数分别是_____________________
.
2.下面所叙述的两条直线是否垂直?
①两条直线相交所成的四个角相等;
②两条直线相交,有一组邻补角相等;
③两条直线相交,对顶角互补.
解:①②③都是垂直的.
3.如图所示,AB⊥CD,垂足为
O,OE是一条射线,且∠AOE
=
35°求∠BOE、∠COE
的度数.
解:因为
AB⊥CD,
所以∠AOC
=
90°.
因为∠AOE
=
35°,
所以∠COE
=
55°.
因为
AB⊥CD,
所以∠COB
=
90°,
所以∠BOE
=
145°.
4.
如图,直线
AB、CD相交于点
O,OD平分∠AOF,
OE⊥CD于点
O,∠1=50°,求∠COB、∠EOB、∠BOF
的度数.
解:因为
OE⊥CD,
所以∠DOE
=
90°,∠COE
=
90°.
因为∠1
=
50°,所以∠AOD
=
40°.
所以∠COB=40°.
所以∠EOB
=
130°.
因为
OD平分∠AOF,所以∠DOF
=
∠AOD
=
40°.
所以∠BOF
=
180°-∠COB-∠DOF
=
100°.
课堂小结
在同一平面内,垂直于同一条直线的两条直线互相平行.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条直线.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
垂
线
第4章
相交线与平行线
湘教版·七年级数学下册
上课课件
学习目标
【知识与技能】
了解垂线的概念及垂线的有关性质.
【过程与方法】
经历观察、操作、交流、归纳、概括等活动,进一步发展空间概念,提高动手操作技能.
【情感态度】
培养学生合作交流的方法和意识,以及在实际生活中应用数学的意识.
【教学重点】
垂线的概念及垂线的有关性质.
【教学难点】
垂线的应用.
情境导入
如图,取两根木条
a、b,将它们钉在一起,固定木条
a,转动木条
b.
当
b
的位置变化时,a、b
所成的角
α
是如何变化的?其中会有特殊情况出现吗?当这种情况出现时,a
与
b
是什么位置关系?
画框的边线,十字路口两条笔直的街道,屋架的横梁与支撑梁等都相交成多少度的角?
观察下图,直线
AB
与直线
CD
有什么位置关系?∠AOD
有多少度?
它们的交点叫做垂足.
两条直线相交所成的四个角中,有一个角是直角时,这两条直线叫做互相垂直.
其中一条直线叫做另一条的垂线.
“垂直”用符号“⊥”表示.
如图,直线
AB
与CD互相垂直,记做“AB⊥CD”.
读做“AB
垂直于
CD”.
观察下图,直线
AB
与直线
CD
有什么位置关系?∠AOD
有多少度?
你能举出一些生活中与垂直有关的实例吗?
两条直线相交不成直角时,其中一条直线叫做另一条直线的斜线,它们的交点叫做斜足.
如图,直线
CD
是
AB
的斜线,同样,直线
AB
也是
CD
的斜线,点
O
是斜足.
(1)如图,在同一平面内,如果
a⊥l,b⊥l,那么
a
//
b
吗?
因为
a⊥l,
b⊥l,
所以∠1
=∠2
=
90
°
,
所以
a∥b
(同位角相等,两直线平行).
(2)如图,在同一平面内,如果直线
a∥b,l⊥a,那么
l
⊥
b
吗?
因为
l⊥a,所以∠1
=
90°.
因为
a∥b,
所以∠2=∠1=90°(两直线平行,同位角相等),
因此
l
⊥
b.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条.
在如图的简易屋架中,BD,AE,HF
都垂直于
CG,若∠1
=
60°,求∠2
的度数.
解:
因为
BD,AE
都垂直于
CG,
所以∠BDC
=∠AEC
=
90
°
.
所以
BD∥AE
(同位角相等,两直线平行).
从而∠2
=∠1
=
60°(两直线平行,
同位角相等).
如图,已知
CD⊥
AB,∠1=∠2,求∠BFE
的度数.
解:
因为
CD⊥AB,
所以∠BDC
=
90°.
又因为∠1
=∠2,
所以
DC∥EF
(
).
所以∠BEF
=∠BDC
=
90°
(
).
同位角相等,两直线平行
在同一平面内,如果一条直线垂直于
两条平行线中的一条,那么这条直线垂直于另一条
练
习
解:因为
EO⊥CD,所以∠COE=∠DOE=90°.
因为∠BOE
=
60°,所以∠BOD
=
30°,
所以
∠AOC
=
∠BOD
=
30°(对顶角相等)
1.
如图,直线
AB,CD
相交于点
O,
EO⊥CD,
∠BOE
=
60°,求∠AOC
的度数.
2.
如图,
DA⊥AB,CD⊥DA,∠B=56°,求∠C.
解:因为
DA⊥AB,
CD⊥DA,
所以
CD∥
AB
.(在同一平面内,垂直于同一条直线的两条直线平行)
所以∠B
+∠C=180°,
所以∠C
=180°-56°=124°
随堂演练
110°、70°、110°
1.
两条直线相交形成四个角,如果其中一个角为70°,则另外三个角的度数分别是_____________________
.
2.下面所叙述的两条直线是否垂直?
①两条直线相交所成的四个角相等;
②两条直线相交,有一组邻补角相等;
③两条直线相交,对顶角互补.
解:①②③都是垂直的.
3.如图所示,AB⊥CD,垂足为
O,OE是一条射线,且∠AOE
=
35°求∠BOE、∠COE
的度数.
解:因为
AB⊥CD,
所以∠AOC
=
90°.
因为∠AOE
=
35°,
所以∠COE
=
55°.
因为
AB⊥CD,
所以∠COB
=
90°,
所以∠BOE
=
145°.
4.
如图,直线
AB、CD相交于点
O,OD平分∠AOF,
OE⊥CD于点
O,∠1=50°,求∠COB、∠EOB、∠BOF
的度数.
解:因为
OE⊥CD,
所以∠DOE
=
90°,∠COE
=
90°.
因为∠1
=
50°,所以∠AOD
=
40°.
所以∠COB=40°.
所以∠EOB
=
130°.
因为
OD平分∠AOF,所以∠DOF
=
∠AOD
=
40°.
所以∠BOF
=
180°-∠COB-∠DOF
=
100°.
课堂小结
在同一平面内,垂直于同一条直线的两条直线互相平行.
在同一平面内,如果一条直线垂直于两条平行线中的一条,那么这条直线垂直于另一条直线.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
